الفيزياء فصل أول

تتحرك الكثير من الأجسام التي نشاهدها حركة دورانية، ومنها أقراص CD وإطارات السيارات وشفرات المراوح،

وتوصف الحركة الدورانية باستخدام مفاهيم خاصة؛ مثل العزم والسرعة الزاوية والتسارع الزاوي والزخم الزاوي.  

أتأمل الصورة

مدينة الألعاب 

تتحرك الأجزاء المختلفة للعبة الدوارة بسرعات وتسارعات مختلفة، وتعمل على مسارعة راكبيها

بطرائق عدة، بحيث تحققلهم الإثارة، فهل تنطبق قوانين نيوتن على الحركة الدورانية؟ وما الكميات

الفيزيائية التي نحتاجها لوصف حركة جسم  يتحرك حركة دورانية؟

الإجابة: تتحقق قوانين نيوتن في الحركة الدورانية مثلها في ذلك مثل الحركة الخطية، وتخضع حركة

العربات لقوانين الحركة الدورانية ومبادئها، ويتطلب وصف هذه الحركة معرفة بالعزم لتحديد حالة

الجسم الحركية، إضافة  إلى معرفة الإزاحة الزاوية والتسارع الزاوي ،وغيرها.

تجربة استهلالية                                     

  الراديان

1- الراديان هي وحدة تستخدم لقياس الزوايا، ويعرف الراديان بأنه قياس الزاوية المركزية

 المقابلة لقوس من دائرة طوله يساوي نصف قطر تلك الدائرة.

2- عند قياس الزاوية $\left(\mathrm{\theta }\right)$ بالدرجات والمقابلة لزاوية مقدارها (1rad) نجد أن: 

$\frac{{360}^o}{2\pi }= 1 rad$$°3.57\approx$3                                   

 3-للتحويل بين الدرجات والراديان نستخدم العلاقة: - 

$\left(rad\right) \mathrm{\theta } = \frac{\mathrm{\pi }}{°180}\times \mathrm{\theta }\left(\mathrm{dgree}\right)$                      

تستخدم وحدة الراد عند دراسة ديناميكا الحركة الدورانية، لوصف مفاهيم الإزاحة الزاوية

 والسرعة الزاوية والتسارع الزاوي. 

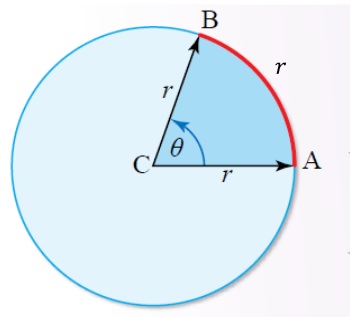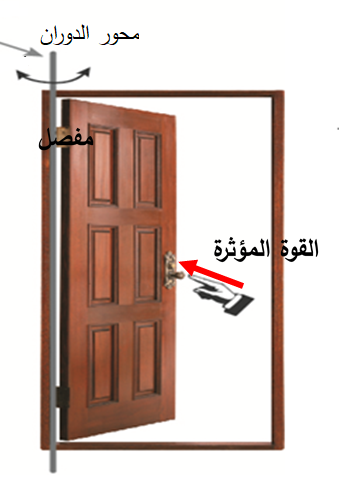
العزم  Torque

في الحياة اليومية نشاهد أجساما تتحرك حركة دورانية، فمثلا  يدور الباب عند  

التأثير فيه بقوة في المقبض المثبت عند طرفه. ومحور الدوران في هذه الحالة 

هو  خط وهمي يمر عبر  مفصلات الباب المثبتة عند الطرف المقابل للمقبض. 

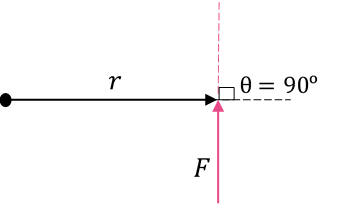
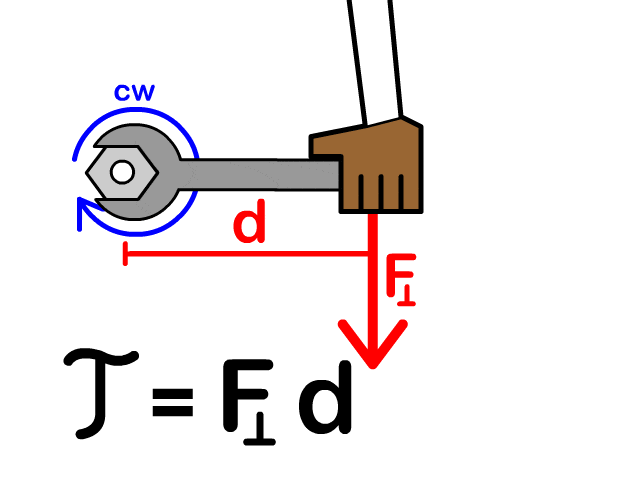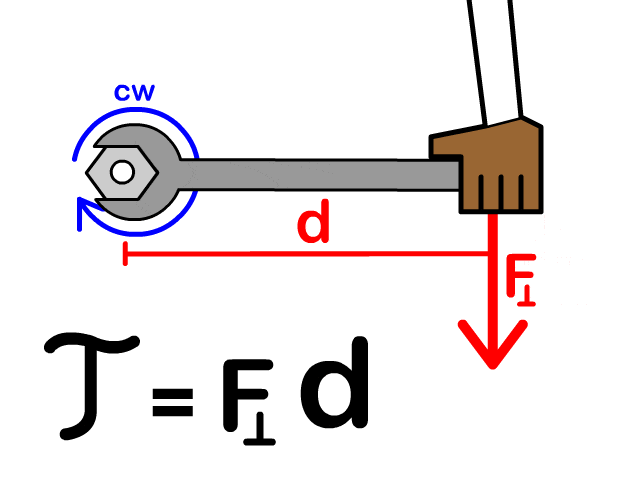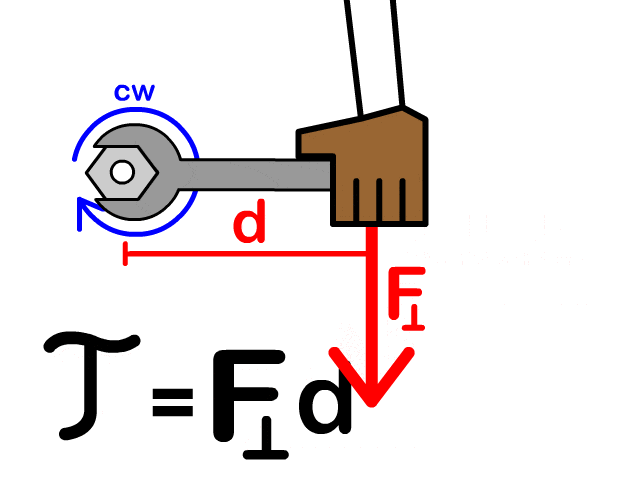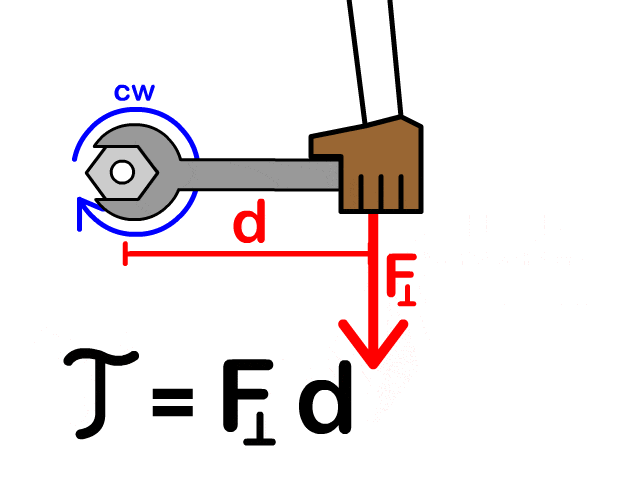
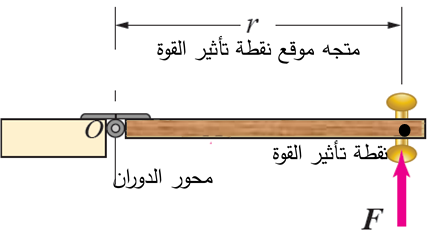
ما المقصود بالعزم وكيف نعبر عنه رياضيا ؟

يعد العزم Torque مقياس لمقدرة القوة على إحداث دوران  لجسم.وهو كمية 

متجهة رمزه $\left(\tau \right)$. ويعرف العزم رياضيا بأنه ناتج الضرب المتجهي لمتجه القوة $\left(F\right)$،

ومتجه موقع نقطة تأثير القوة$\left( r\right)$ الذي يبدأ من نقطة على محور الدوران وينتهي

عند نقطة تأثير القوة.

يقاس العزم بوحدة (N.m) ويعبر عنه بالمعادلة الآتية: 

$\mathit{F}\mathbf{\times }\mathit{r}\mathbf{=}\mathit{\tau }$

ويحسب مقدار العزم كما يأتي: 

$\mathbf{ }\mathit{\tau }\mathbf{=}\mathit{r}\mathbf{ }\mathit{F}\mathbf{ }\mathit{s}\mathit{i}\mathit{n}\mathbf{\theta }$

حيث $\left(\mathrm{\theta }\right)$ الزاوية المحصورة بين المتجهين $\left(F\right) و \left(r\right)$ 

المنظر العلوي لباب تؤثر  فيه قوة في المقبض 

  المثبت عند طرفه، فتعمل على تدويره.

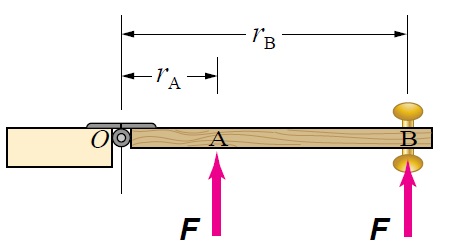
العوامل التي يعتمد عليها العزم 

  يبين الشكل (أ) المنظر العلوي لباب تؤثر فيه  قوة عمودية على مستوى الباب، ويبين

الشكل (ب) الباب نفسه  عندما تؤثر فيه القوة عند الموقع نفسه بشكل مائل. يسمى

الخط المرسوم على امتداد متجه القوة بخط عمل القوة، ونحصل عليه برسم خط  ينطبق

على متجه القوة. ويسمى البعد العمودي  بين محور الدوران وخط عمل القوة ذراع القوة

 Lever arm، ونحصل عليه برسم خط يبدأ من موقع محور الدوران (O) ويصل إلى خط عمل

القوة بحيث يكون عموديا عليه. 

(أ): قوة تؤثر عموديا على مستوى الباب.                                                             (ب): قوة تؤثر بشكل مائل على مستوى الباب. 

وللتوصل إلى العوامل التي يعتمد  عليها العزم، أتأمل الشكلين (أ)، (ب)  وألاحظ ما يأتي:

• عندما يكون اتجاه القوة المؤثرة  $\left(F\right)$ عموديا على مستوى الباب$\left(°90=\mathrm{\theta }\right)$، فإن طول

     ذراع القوة يكون أكبر  ما يمكن ويساوي مقدار المتجه $\left(r\right)$ .

•  عندما لا يكون اتجاه القوة المؤثرة $\left(F\right)$ عموديا على مستوى الباب ، فإن طول ذراع القوة

       يساوي $\left(r \sin \alpha \right)$، وهو  نفسه  $\left( r\mathrm{sin\theta }\right)$؛ لأن مجموع الزاويتين يساوي $\left(°180\right)$، فيكون $\left(\mathrm{\theta } \sin =\alpha \sin \right)$.

•   ينعدم  العزم  عندما يَمُر  خط  عمل  تأثير القوة بمحور  الدوران$\left(\mathrm{\theta } =0\right)$ ، ويزداد  العزم بزيادة القوة 

         مع ثبات  ذراع  القوة.

  نستنتج مما سبق أن مقدار العزم يتناسب طرديا مع كل من:  مقدار القوة المؤثرة ، وطول ذراع القوة . 

سؤال: عند فتح الباب نؤثر بقوة عمودية على مقبض الباب المثبت عند طرفه. 

    الحل:

      وذلك للحصول على أكبر عزم ممكن، فالتأثير  بقوة عند النقطة (B) عوضا عن 

      التأثير بها عند النقطة (A) بالقرب من محور الدوران، يجعل نقطة تأثير  القوة  

      أبعد ما يمكن عن محور الدوران. كذلك يزداد العزم عندما تؤثر هذه القوة عموديا؛ 

      لذلك لا ندفع الباب بقوة جانبية.  

  كلما زاد بعد  نقطة تأثير القوة   عن محور الدوران يزداد العزم. 

سؤال: يبين الشكل المجاور المنظر العلوي لباب تؤثر فيه ثلاث قوى متساوية  

في المقدار  عند الموقع نفسه، أرتب العزم الناتج عن  هذه القوى تنازليا. 

الحل:  

$\left({}_3\tau \right)<\left({}_2\tau \right)<\left({}_1\tau \right)$

التفسير: لمعرفة العزم الناتج عن القوى  نستخدم العلاقة $\left( \mathrm{\theta } \sin F r=\tau \right)$؛ القوى 

الثلاث متساوية في المقدار، ومختلفة في طول ذراع القوة. وبما أن $\left({}_{1}F\right)$ تؤثر عموديا،  

يكون لها أكبر ذراع قوة وأكبر عزم. تليها $\left({}_{2}F\right)$ حيث يكون ذراعها أصغر من ذراع $\left({}_{1}F\right)$.   

أما  القوة $\left({}_{3}F\right)$ فإن عزمها يساوي صفر؛ لأن خط عملها يمر  بمحور الدوران.

 القوى الثلاث متساوية في   المقدار  وتؤثر عند الموقع   نفسه، إلا أن العزم الناتج عن القوى غير متساو بسبب اختلاف اتجاهاتها. 

$\gg$ أتحقق ( صفحة 41 في الكتاب) 

ما المقصود بالعزم؟  وعلام يعتمد؟ 

يعد العزم مقياسا  لمقدرة القوّة على إحداث دورانٍ لجسم، وهو كمية متجهة،  

رمزه $\left(\tau \right)$،ويحسب مقداره بالعلاقة $\mathrm{(}\mathrm{ }\mathrm{\tau }\mathrm{=}\mathit{r}\mathrm{ }\mathit{F}\mathit{ }\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\theta }\mathrm{)}$، ويقاس العزم بوحدة $\left( \mathrm{m}.\mathrm{N}\right)$  

حسب النظام الدولي للوحدات. ويتناسب مقدار العزم طرديا مع كل من مقدار  

إشارة العزم

بما أن العزم كمية متجهة، فإننا نعده موجبا عندما يسبب دوران الجسم في عكس اتجاه حركة    

عقارب الساعة، ونعده سالبا عندما يسبب دوران الجسم في اتجاه حركة عقارب الساعة.  

       حركة عقارب الساعة       

إشارة العزم موجبة

(الدوران عكس حركة عقارب الساعة)

إشارة العزم سالبة

(الدوارن باتجاه حركة عقارب الساعة)

عكس حركة عقارب الساعة  

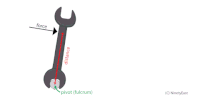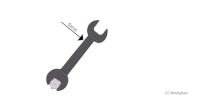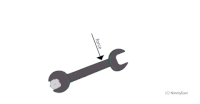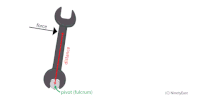
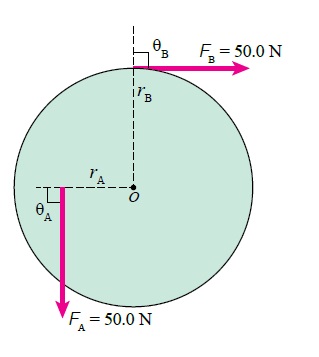
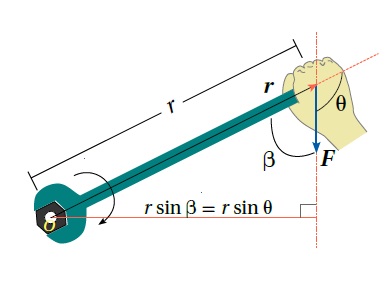
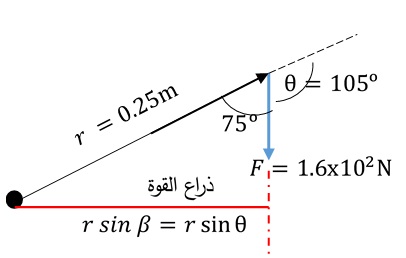
المثال (1) (صفحة 42 في الكتاب) 

يستخدم زيد مفتاح شد طوله $\left(25.0 \mathrm{cm}\right)$ لشد صامولة في دراجة، حيث أثر  بقوة مقدارها          

$\left( \mathrm{N} {}^2 10\times 6.1\right)$ ، في طرف مفتاح الشد في الاتجاه المبين في  الشكل،فإذا علمت أن مقدار 

  الزاوية $\left(\beta \right)$ يساوي $\left(°75\right)$. أحسب مقدار العزم المؤثر في المفتاح، وأحدد اتجاهه.

المعطيات:

 $965.0\approx °105\sin$ ,$°105=75- 180=\mathrm{\theta },°75= \mathrm{\beta },\mathrm{N} {}^{2}10\times 6.1=F,\mathrm{cm}25.0=\mathrm{cm} 0.25=r$  

المطلوب:                                                                                                                           $?=\tau$   

الحل: 

 تعمل القوة على تدوير الجسم باتجاه  حركة عقارب الساعة فيكون العزم سالبا، ويحسب 

باستخدام العلاقة الخاصة بحساب العزم مع إضافة إشارة سالبة. 

$\mathrm{\theta } \sin F r-=\tau$   

  $\mathrm{m}.\mathrm{N} 6.38-$= $°105\sin \times {}^{2}10\times 6.1 \times 25.0-=$   

سؤال: يبين الشكل المجاور مفتاح يستخدم لفك صامولة، معتمدا على الشكل، أجب عن 

   الأسئلة الآتية:  

أولا: أي من الرموز المثبتة على الشكل يعبر عن : 

       أ. الزاوية بين متجه القوة ومتجه موقع نقطة تأثير القوة.

       ب. ذراع القوة. 

ثانيا: أحدد اتجاه دوران المفتاح. 

الحل: 

أولا:  أ. $\left(\beta \right)$  ب. (c)       ثانيا: عكس اتجاه حركة عقارب الساعة. 

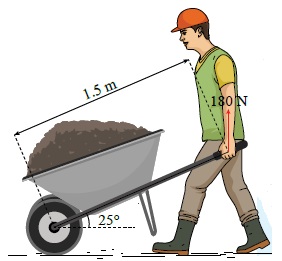
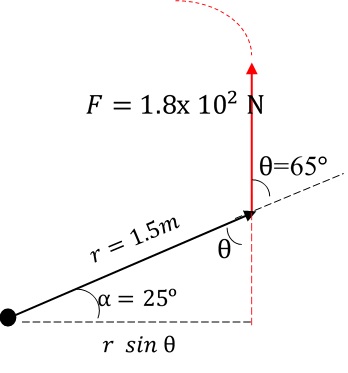
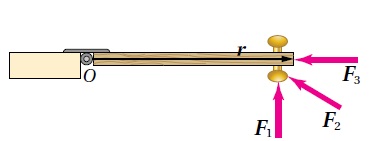
تمرين (صفحة 43 في الكتاب) 

يدفع عامل عربة كما هو موضح في الشكل، عن طريق التأثير في مقبضي ذراعيها بقوتين مجموعهما

 $\left(\mathrm{N}{}^2 10\times 8.1=F\right)$ رأسيا إلى أعلى لرفعهما إلى أعلى بزاوية $\left(°25\right)$ بالنسبة إلى محور  $\left(+x\right)$. إذا علمت  

 أن بعد كل من مقبضي محور الدوران يساوي $\left(\mathrm{m} 5.1\right)$. أحسب مقدار عزم القوة  $\left(F\right)$ المؤثر في 

 العربة حول محور الدوران، وأحدد اتجاهه. 

المعطيات:

 $9.0\approx 65 \sin$ , $\theta ={90}^o - {25}^o = {65}^o$,$\mathrm{m} 5.1=r$ ,$\mathrm{N} {}^{2 }10\times 8.1=F$         

المطلوب:                                                                                                             $?=\tau$   

 الحل:

يحسب العزم باستخدام العلاقة :   

                                                                                                       $\mathrm{\theta } \sin F r=\tau$      

 $\mathrm{m}.\mathrm{N}243$ =$9.0\times {}^{2}10\times 8.1\times 5.1$ =$65 \sin \times {}^2 10\times 8.1\times 5.1=\tau$     

العزم موجب؛ لأن قوة العامل تعمل على تدوير العربة بعكس اتجاه حركة عقارب الساعة حول

محور دورانها.

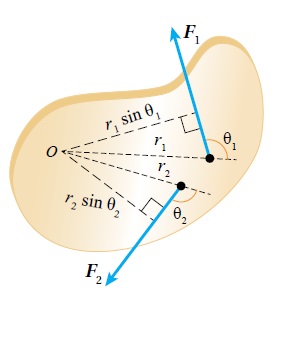
إيجاد العزم المحصل Finding Net Torque

يحسب العزم المحصل المؤثر في جسم عندما تؤثر فيه أكثر من قوة بحساب العزم الناتج عن كل  

 قوة على حدة ، حول محور الدوران ؛ مع مراعاة اتجاه الدوران. ثم تجمع العزوم مع إشاراتها، لإيجاد

العزم المحصل ورمزه $\left(\sum \tau \right)$: 

                                                                 $\mathbf{\sum }\mathbf{ }\mathit{\tau }\mathbf{ }\mathbf{=}{\mathit{\tau }}_{\mathbf{1}}\mathbf{ }\mathbf{+}{\mathit{\tau }}_{\mathbf{2}}\mathbf{ }$                             

  وتدل إشارة  $\left(\sum \tau \right)$ على إشارة العزم المحصل.               

 فمثلا في الشكل المقابل، تؤثر في الجسم قوتين: القوة$\left({}_{1}F\right)$ تعمل على تدويره عكس اتجاه 

 حركة عقارب الساعة، والقوة $\left({}_{2}F\right)$ تعمل على تدويره باتجاه حركة عقارب الساعة. فيكون العزم

 المحصل المؤثر فيه: 

                                      $\sum \tau = F_1 r_1 sin {\mathrm{\theta }}_1 -F_2 r_2 sin {\mathrm{\theta }}_2$

تعمل $\left({}_{1}F\right)$ على تدوير الجسم عكس عقارب الساعة فيعوض العزم (+).

تعمل $\left({}_{2}F\right)$ على تدوير الجسم باتجاه عقارب الساعة فيعوض العزم (-)

المثال (2) (صفحة 43 في الكتاب) 

بكرة مصمتة نصف قطرها $\left({}_{\mathrm{B}}r\right)$ يمر في مركزها (O)محور دوران عمودي على مستوى الصفحة، 

  إذا علمت أن القوة $\left({}_{\mathrm{A}}F\right)$ تؤثر في البكرة على بعد $\left( r_{\mathrm{A}} =30.0 \mathrm{cm}\right)$ من محور الدوران، وتؤثر 

القوة $\left({}_{\mathrm{B}}F\right)$عند  حافة البكرة حيث  $\left(\mathrm{m} \mathrm{c} 0.50= {}_{\mathrm{B}}r\right)$. واعتمادا على المعلومات المثبتة في الشكل،

 أحسب العزم المحصل المؤثر  في البكرة، وأحدد اتجاهه.

المعطيات: 

 $°90= {}_{\mathrm{B}}\mathrm{\theta }= {}_{\mathrm{A}}\mathrm{\theta } ,\mathrm{m}50.0= \mathrm{cm} 0.50 ={}_{\mathrm{B}}r, \mathrm{m}30.0=\mathrm{cm} 0.30={}_{\mathrm{A}}r ,\mathrm{N} 50={}_{\mathrm{B}}F= {}_{\mathrm{A}}F$    

المطلوب:                                                                                                           $\left(\sum \tau =? \right)$ 

الحل:    

تعمل القوة $\left({}_{\mathrm{A}}F\right)$ على تدوير البكرة بعكس اتجاه حركة عقارب الساعة حول محور دورانها  

 الذي يمر بالنقطة $\left(\mathrm{o}\right)$، لذا يكون عزمها موجباً. وتعمل القوة $\left({}_{\mathrm{B}}F\right)$ على تدوير الجسم باتجاه  

حركة عقارب الساعة حول محور الدوران نفسه، لذا يكون عزمها سالباً. ويحسب العزم 

المحصل من العلاقة: 

$\sum \tau = {\tau }_1+ {\tau }_2$            

    $= F_{\mathrm{A}} r_{\mathrm{A} } \sin {\mathrm{\theta }}_{\mathrm{A} } -F_{\mathrm{B}} r_{\mathrm{B}} \sin {\mathrm{\theta }}_{\mathrm{B}}$                    

$= 50 \times 0.30\times \sin {90}^o - 50 \times 0.50 \sin {90}^o$                   

$\mathrm{m}.\mathrm{N} 10-=25 -15=$                  

العزم المحصل سالب

 فيعمل على تدوير البكرة 

 باتجاه حركة عقارب الساعة.

سؤال:  في الشكل المجاور ، أحسب العزم المحصل حول محور دوران يمر بالنقطة(O )،  

                 وأحدد  اتجاهه. 

الحل: 

$\sum \tau = {\tau }_1+{\tau }_2$  

   $= - F_1 r_1 sin {\mathrm{\theta }}_1 + F_2 r_2 sin {\mathrm{\theta }}_2$         

  $= - 8\times 0.25\times 1+10\times 0.75 \times 1$        

$= -2 + 7.5 =5.5 \mathrm{N}.\mathrm{m}$         

إشارة العزم المحصل(+)؛ اتجاهه عكس حركة عقارب الساعة.       

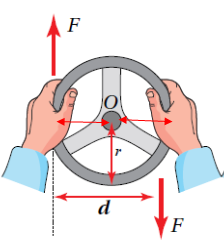
الازدواج Couple

يوضح الشكل المجاور منظرا علويا لمقود سيارة نصف قطره $\left(r\right)$، المقود قابل للدوران حول 

 محور يمر بالنقطة(O). تؤثر اليد اليمنى بقوة مقدارها$\left(F_{}\right)$ عموديا إلى أسفل تؤدي إلى دورانه 

 باتجاه حركة عقارب الساعة. بينما تؤثر اليد اليسرى بقوة $\left(F_{}\right)$ عموديا إلى أعلى تؤدي إلى دورانه

باتجاه حركة عقارب الساعة أيضا.

يمكن حساب العزم المحصل حول محور الدروان نفسه باستخدام العلاقة:

$\sum \tau = {\tau }_1+ {\tau }_2$          

وبما أن القوتين تؤثران عموديا $\left(\mathrm{\theta }=90°\right)$، وذراع القوة لكل منهما $\left(r\right)$: 

$\sum \tau = -Fr - F r =-2Fr$          

ألاحظ أن $\left(d=2r\right)$ حيث $\left(d\right)$ البعد العمودي بين خطي عمل القوتين: 

$\sum \tau = -F d$          

والإشارة السالبة في هذه العلاقة تدل على أن المقود يدور باتجاه حركة عقارب الساعة. 

  تشكل القوتان المؤثرتان في المقود

ازدواجا يعمل على تدويره باتجاه حركة 

 عقارب الساعة.

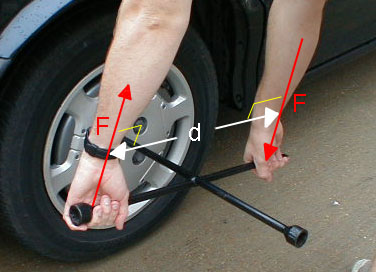
تشكل القوتان  المؤثرتان في مفتاح الشد  المبين في الشكل ازدواجا. 

     ماذا نستنتج مما سبق؟

• تشكل القوتان المؤثرتان في مقود السيارة ما يعرف بالازدواج Couple.
• يمكن تعريف الازدواج بأنه قوتان متساويتان مقدارا ومتعاكستان اتجاها وخطا عملهما غير متطابقين.
• يعمل الازدواج على تدوير الجسم حول محور دوران ثابت، ويسمى العزم الناتج منه عزم الازدواج $\left({\tau }_{couple}\right)$، ويساوي ناتج ضرب إحدى القوتين في البعد العمودي بينهما.

• عموما عندما تصنع قوتا الازدواج زاوية غير قائمة مع المتجه $\left(r\right)$ فإن عزم الازدواج يساوي:   

                                                                       ${\tau }_{couple }= F r \sin \mathrm{\theta } + F r \sin \mathrm{\theta } = F\left(2 r \sin \mathrm{\theta }\right)$ 

       وبما أن $\left(d=2 r \sin \mathrm{\theta } \right)$ فإن عزم الازدواج يعطى بالعلاقة الآتية:

                                                       ${\tau }_{couple}=F d$   

حيث: $\left(F\right)$ إحدى القوتين، $\left(d\right)$ البعد العمودي بينهما. وقد يكون العزم موجبا أو سالبا حسب

اتجاه الدوران؛فمثلا يعمل الازدواج المبين في الشكل، على تدوير القضيب الفلزي بعكس اتجاه

حركة عقارب الساعة، حول محور ثابت عمودي على مستوى الصفحة، يمر بالنقطة(O)؛ فتكون

إشارةالعزم موجبة. 

 يعمل الازدواج  على تدوير القضيب   الفلزي بعكس اتجاه حركة عقارب   الساعة حول محور ثابت يمر   بالنقطة(O).

$\gg$ أتحقق (صفحة 44 في الكتاب) 

ما المقصود بعزم الازدواج؟ وعلام يعتمد؟

هو العزم الناتج عن تأثير قوتين متساويتين مقدارًا ومتعاكستين اتجاهًا وخطّي عملهما  غير منطبقين.   

 وهو يعتمد على كل من:مقدار إحدى القوّتين المتساويتين، والبُعد العمودي بينهما.

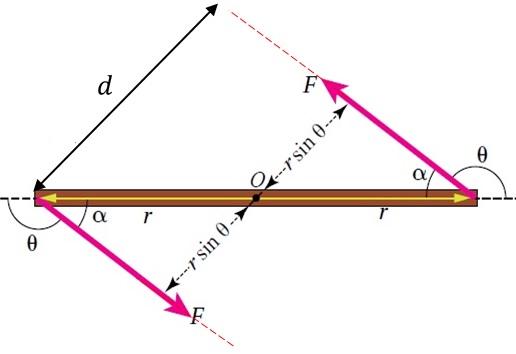
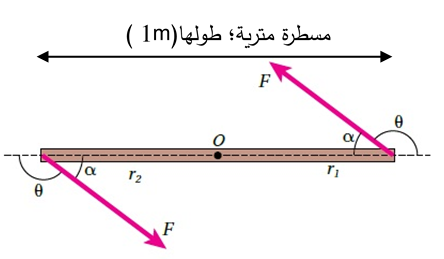
المثال (3) (صفحة 45 في الكتاب)

مسطرة مترية فلزية قابلة للدوران حول محور ثابت عمودي على مستوى الصفحة يمر  في

 منتصفها عند النقطة(O)، كما هو موضح في الشكل. أثر فيها قوتان شكلتا ازدواجا، إذا 

  علمت أن مقدار كل من القوتين(80N) ومقدار الزاوية $\left(\mathrm{\theta }\right)$ يساوي $\left(°143\right)$. أحسب مقدار

عزم الازدواج المؤثر  في المسطرة، وأحدد اتجاهه.

المعطيات: 

$°143={}_2\mathrm{\theta }= {}_1\mathrm{\theta }, \mathrm{m}5.0= \mathrm{cm} 0.50= {}_{2}r={}_{1}r ,\mathrm{N}0.80={}_{2}F ={}_{1}F$

المطلوب: 

$? ={}_{elpuoc}\tau$

الحل: 

تشكل القوتان ازدواجا يعمل على تدوير المسطرة بعكس اتجاه حركة عقارب الساعة حول

محور ثابت يمر بالنقطة (O). ويحسب من العلاقة:

$\left( \mathrm{\theta } \sin r2\right) F=d F={}_{elpuoc}\tau$

 $\mathrm{m}.\mathrm{N} 48= 6.0\times 80 =°143\sin 5.0 \times 2\times 80=$             

 يعمل العزم على تدوير المسطرة 

 بعكس اتجاه حركة عقارب الساعة

سؤال: يبين الشكل قضيبين فلزيين (A, B) متماثلين، يؤثر في كل منهما القوى نفسها، وبالاتجاهات

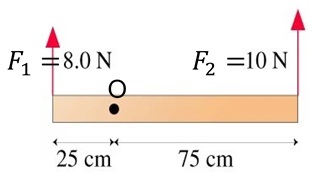
 المبينة على الشكل. و القضيبان قابلان للدوران حول محور يمر بالنقطة (O)المبين لكل منهما.

 أقارن بين العزم المحصل المؤثر في كليهما.  أختار الإجابة الصحيحة مما يأتي: 

     أ. $\left(\sum {\tau }_{B }\right)<\left( \sum {\tau }_{A }\right)$               ب. $\left(\sum {\tau }_{\mathrm{B}}\right) > \left(\sum {\tau }_{\mathrm{A}}\right)$                 ج.$\left(\sum {\tau }_{\mathrm{B}}\right) = \left(\sum {\tau }_{\mathrm{A}}\right)$ 

الحل: 

ج. $\left({}_{\mathrm{A}}\tau \right) = \left({}_{\mathrm{B}}\tau \right)$.

التفسير: نحسب مجموع العزوم الناتج عن القوتين لكل جسم :  

 $$\begin{gathered} \sum {\tau }_{\mathrm{A}} =- F\times 0.2-F\times 0.2= -0.4 F \\ \sum {\tau }_{\mathrm{B}} =- F\times 0.1-F\times 0.3= -0.4 F \end{gathered}$$

 سؤال:  في الشكل (A) يؤثر في القرص ازدواج مقدار كل من  قوتيه $\left({}_{1}F\right)$، وفي الشكل(B) يؤثر في 

 القرص ازدواج مقدار كل من قوتيه  $\left({}_{2}F\right)$ إذا علمت أن العزم المؤثر في القرص متساو في الحالتين،  

 فما مقدار النسبة $\left(\frac{{}_{2}F}{{}_{1}F}\right)$ ؟

أختار الإجابة الصحيحة مما يأتي:

أ. $\frac{1}{4}$                   ب.$\frac{3}{4}$                      ج.$\frac{4}{3}$                     د. 1 

الحل: (ب. $\frac{3}{4}$  )   

التفسير: بما أن العزم المؤثر في القرص متساو في الحاتين: 

       $\frac{3}{4}=\frac{{}_{2}F}{{}_{1}F}\Rightarrow$$4.0\times {}_{ 2}F=3.0\times {}_{1}F\Rightarrow$ ${}_{2}d {}_{2}F= {}_{1}d {}_{1}F\Rightarrow {}_2\tau ={}_1\tau$     

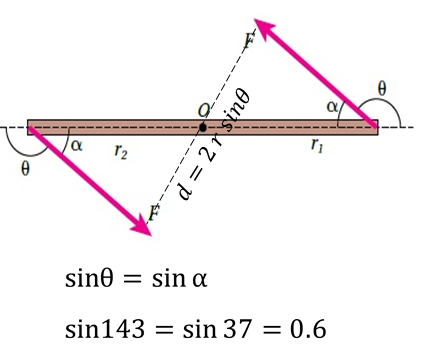
الاتزان 

درست في صفوف سابقة أن الأجسام الساكنة تكون في حالة اتزان سكوني، والأجسام

 المتحركة بسرعة ثابتة وبخط مستقيم تكون في حالة اتزان انتقالي، وفي الحالتين تكون

  القوة المحصلة المؤثرة فيها تساوي صفر؛ $\left(\sum F=0 \right)$.

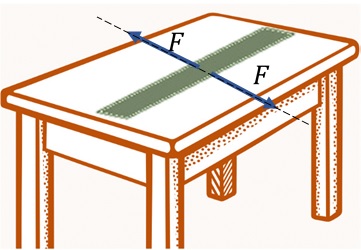
يبين الشكل (أ) مسطرة مترية موضوعة على طاولة، وتؤثر فيها قوتان متساويتان

 مقدارا  ومتعاكستان اتجاها، في الموقع نفسه، فتكون محصلة القوتان تساوي صفر

$\left(\sum F=0 \right)$، وتكون المسطرة في حالة اتزان سكوني. 

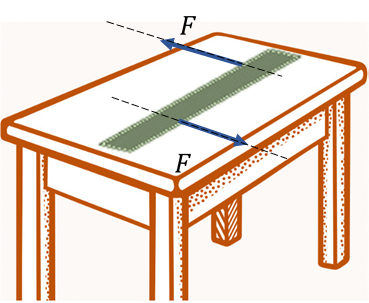
أما الشكل (ب) فيوضح المسطرة نفسها عند تأثير القوتين نفسيهما فيها عند موقعين

 مختلفين، هنا لا تكون المسطرة في حالة اتزان بالرغم من أن القوة المحصلة المؤثرة فيها

 تساوي صفر.. فالمسطرة في هذه الحالة تتحرك حركة دورانية؛ لأن خطي عمل القوتين

 المؤثرتين فيها غير متطابقين، فيكون العزم المحصل المؤثر فيها لا يساوي صفر.  

نستنتج مما سبق أنه كي يكون الجسم في حالة اتزان سكوني عندما تؤثر فيه قوى عدة،

 يجب أن يتحقق الشرطين الآتيين معا:

الشرط الأول: أن تكون القوة المحصلة المؤثرة فيه تساوي صفرا:

                                                                                .$\left(\sum F=0\right)$

                                                       $\underset{ }{\sum F_x= 0 , \sum _{ }{F}_y=0}$                                                 

الشرط الثاني: أن يكون العزم المحصل المؤثر فيه يساوي صفرا. $(\sum \tau =0)$

  الشكل(أ):المسطرة تتأثر بقوتين        متساويتين ومتعاكستين وخطا       عملها متطابقين فتكون في حالة       اتزان سكوني .   

 الشكل (ب): المسطرة تتأثر بقوتين   متساويتين ومتعاكستين وخطا   عملهما غير متطابقين، فتشكلان   ازدواجا يعمل على تدويرها، فتكون   غير متزنة. 

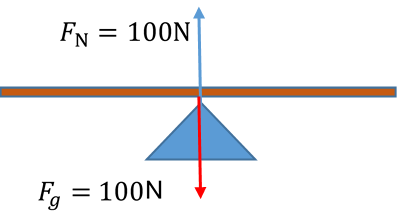
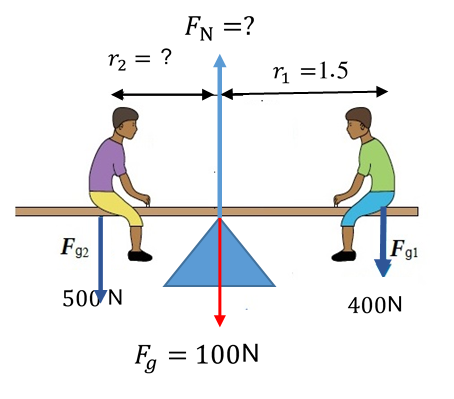
تطبيق شرطا الاتزان 

  تتكون لعبة (See-Saw) المبينة في الشكل المجاور من لوح خشبي منتظم، وزنه (100N)يؤثر

 في منتصفه، ويرتكز اللوح  على دعامة  موضوعة عند منتصفه، وهو في حالة اتزان سكوني. 

• ما القوى  المؤثرة في اللوح؟ وما مقدار كل منها؟

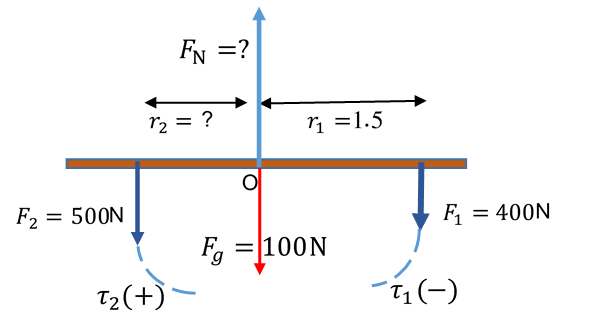
  يتأثر اللوح بقوتين هما الوزن $\left( {}_{g}F\right)$إلى الأسفل، والقوة العمودية $\left({}_{\mathrm{N}}F\right)$ التي تؤثر 

 بها الدعامة إلى الأعلى. وبما أن اللوح في حالة اتزان سكوني فإن: $\mathrm{N} 100= {}_{g}F={}_{\mathrm{N}}F$

يصعد على اللوح طفل وزنه $\left(\mathrm{N}400={}_{1g}F\right)$ ويجلس على بعد $\left(\mathrm{m} 5.1={}_{1}r\right)$ من نقطة 

الارتكاز، ثم يصعد طفل وزنه $\left( \mathrm{N}500={}_{2 g}F\right)$ فيتزن اللوح عندما يجلس على بعد $\left(r_2\right)$ من

 نقطة الارتكاز. أحسب:

أ. مقدار القوة العمودية$\left({}_{\mathrm{N}}F\right)$       ب. بعد الطفل الثاني عن نقطة الارتكاز $\left({}_{2}r\right)$

يتأثر اللوح بأربع قوى هي: $( {}_{2g}F ,{}_{1g}F,{}_{ g}F)$ اتجاهها للأسفل، $\left({}_{\mathrm{N}}F\right)$ اتجاهها للأعلى وبما أن اللوح

متزن ، إذا ينطبق عليه شرطا الاتزان:

• بتطبيق الشرط الأول $\left(\sum F=0\right)$ نحسب $\left(F_{\mathrm{N}}\right)$: 

$0=\left( {}_{2g}F+{}_{1g}F+{}_{g}F\right) -{}_{\mathrm{N}}F$

$\mathrm{N}1000=500+400+ 100= {}_{\mathrm{N}}F \Rightarrow {}_{2g}F +{}_{1g}F+ {}_{g}F={}_{\mathrm{N}}F$

• بتطبيق الشرط الثاني $(\sum \tau =0)$ نحسب $\left(r_2\right)$: 

     لتطبيق هذا الشرط  يجب تحديد موقع محور الدوران، وباختيار محور الدوران عند نقطة

    الارتكاز  (O)، يكون عزم كل من $\left({}_{\mathrm{N}}F\right),\left({}_{g}F\right)$ يساوي صفر ؛ لأن  عزم قوة حول محور يمر 

    في نقطة تأثيرها يساوي صفر.

$\sum \tau ={\tau }_1 +{\tau }_2 =0$

$-F_1 r_1 \sin 90+ F_2 r_2 \sin 90 =0$

$-400\times 1.5 + 500\times r_2 =0 \Rightarrow -600+500 r_{2 }=0$

$500 r_2 = 600 \Rightarrow r_2 = \frac{600}{500}=1.2 \mathrm{m}$

   اللوح قبل جلوس الأطفال عليه. تؤثر 

    فيه قوتان؛ الوزن والقوة العمودية.

  اللوح عند جلوس الأطفال عليه. تؤثر فيه 

  أربع قوى. 

  مخطط يبين القوى  المؤثرة في اللوح. 

  وموقع محور الدوران (O).

    ماذا نستنتج مما سبق؟ 

     1.القوة العمودية المؤثرة في اللوح الخشبي زادت عند جلوس الأطفال عليه، وذلك كي يحافظ اللوح على اتزانه.

     2. عزم قوة حول محور يمر في نقطة تأثيرها يساوي صفر، لأن طول ذراع القوة في هذه الحالة يساوي صفر.

    3.كي يتحقق الاتزان، فإن الطفل ذو الوزن الأكبر  يجلس عند نقطة أقرب إلى محور الدوران من الطفل ذو الوزن الأقل ؛

      وذلك كي  يكون مجموع عزميهما صفر، حيث$\left(F_1 r_1 = F_2 r_2\right)$، فالعلاقة بين $\left(F\right)و \left(r\right)$ عكسية بثبوت العزم.

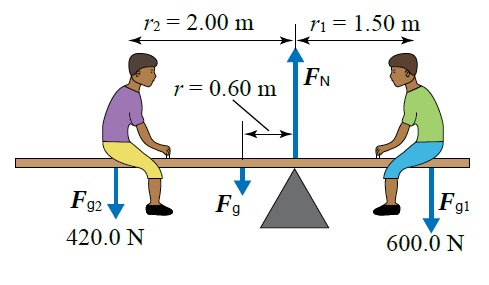
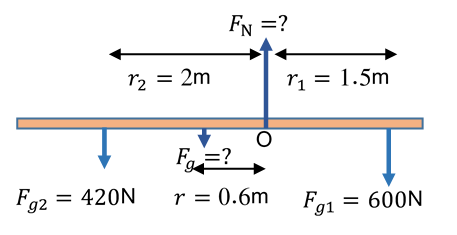
المثال (4) (صفحة 47 في الكتاب)

يجلس فادي$\left(F_{g1}\right)$ وصقر $\left(F_{g2}\right)$ على جانبي لعبة (see-sae)تتكون من لوح خشبي منتظم متماثل

 وزنه $\left(F_g\right)$ يؤثر في منتصفه. يرتكز اللوح على نقطة تبعد $\left(0.6\mathrm{m}\right)$ يمين منتصف اللوح الخشبي،

 كما هو موضح في الشكل. إذا كان النظام المكون من اللعبة والطفلين في حالة اتزان سكوني  

   واللوح الخشبي في وضع اتزان. أحسب ما يأتي: 

أ. وزن اللوح الخشبي $\left(F_g\right)$.  

ب. القوة التي تؤثر بها نقطة الارتكاز في اللوح الخشبي $\left(F_{\mathrm{N}}\right)$.

المعطيات:

 $F_{g1}=600\mathrm{N}, F_{g2}=420\mathrm{N}, r=0.60 \mathrm{m}, r_1=1.50 \mathrm{m}, r_2=2.00\mathrm{m}.$     

المطلوب:                                                                                $F_g=?, F_{\mathrm{N}} =?$

الحل: 

أ.مقداري $\left(F_{\mathrm{N}}\right)و \left(F_g\right)$ غير معلومين، ولحساب أي منهما نطبق الشرط الثاني للاتزان حول محور

ل يمر في إحدى نقطتي تأثير هاتين القوتين؛ فيكون عزم تلك  القوة يساوي صفر . 

( لأن ذراع القوة في هذه الحالة يساوي صفر).  

  $\sum \tau =0$

$F_{g2} \times r_2 +F_g\times r - F_{g1}\times r_1 =0$

$420\times 2+F_g \times 0.6 - 600\times 1.5=0$

$F_g\times 0.6= 900- 840 \Rightarrow F_g = \frac{60}{0.6}=100\mathrm{N}$

ب. نطبق شرط الاتزان الأول باتجاه محور (y)، لأنه لا توجد قوى باتجاه محور (x)

$$\begin{gathered} \sum F_y =m a=0 \\ {F}_{\mathrm{N}} -( F_g +F_{g1}+F_{g2}) =0 \end{gathered}$$

$F_{\mathrm{N} }=F_g +F_{g1}+ F_{g2} =100+600+ 420=1120 \mathrm{N}$

   اللوح يتأثر بأربع قوى. ونقطة الارتكاز     تقع على يمين نقطة المنتصف. 

 نختار  محور الدوران (O)عند نقطة ارتكاز    اللوح. فيكون عزم $\left(F_{\mathrm{N}}\right)$ يساوي صفر.

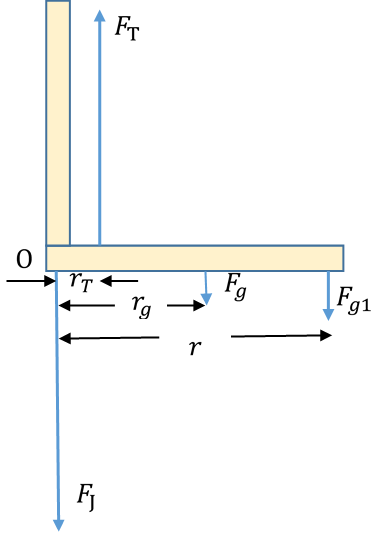
تمرين (صفحة 47 في الكتاب) 

ترفع جمان ثقلا وزنه $\left(40 \mathrm{N}\right)$ في أثناء ممارستها للتمارين الرياضية في ناد رياضي. إذا علمت أن 

 نقطة إلتقاء العضلة ثنائية الرأس بالساعد تبعد $\left(r_{\mathrm{T}} =5.0 \mathrm{cm}\right)$ عن المرفق. ووزن عظم الساعد

 والأنسجة $\left(30\mathrm{N}\right)$، ويؤثر على بعد $\left(r_g =15.0 \mathrm{cm}\right)$ عن المرفق، وبعد نقطة تأثير القوة في اليد

 $\left(r=35.0 \mathrm{cm}\right)$ عن المرفق. والساعد متزن أفقيا  في الوضع الموضح على الشكل.

فاحسب مقدار ما يأتي:

أ. قوة الشد في العضلة $\left(F_T\right)$ المؤثرة في الساعد بافتراضها رأسيا إلى الأعلى.

ب. القوة التي يؤثر بها المرفق في الساعد $\left(F_{\mathrm{J}}\right)$.

المعطيات: 

$\mathrm{cm} 5={}_{\mathrm{T}}r ,\mathrm{cm} 15= {}_{g}r ,\mathrm{cm} 35= r,\mathrm{N} 30={}_{g}F,\mathrm{N}40={}_{1g}F$

المطلوب: 

$?= {}_{\mathrm{J}}F,?={}_{\mathrm{T}}F$

الحل:  

أ. لحساب $\left({}_{\mathrm{T}}F\right)$ نطبق شرط الاتزان الثاني حول محور عمودي عبر  مفصل الساعد والمشار إليه

  بالرمز (O)، فيكون عزم القوة $\left({}_{\mathrm{J}}F\right)$ يساوي صفر. 

$\sum \tau =0$

$$\begin{gathered} F_{\mathrm{T}} r_{\mathrm{T}} - F_g r_g -F_{g1} r =0 \\ {F}_{\mathrm{T}} \times 0.05 -30\times 0.15 -40\times 0.35 =0 \\ 0.05 F_{\mathrm{T}} -4.5 - 14=0 \Rightarrow F_{\mathrm{T}} =\frac{18.5}{0.05}=370 \mathrm{N} \end{gathered}$$

ب. لحساب $\left({}_{\mathrm{J}}F\right)$نطبق شرط الاتزان الأول باتجاه محور (y) : 

$\sum F_y=0$

$$\begin{gathered} F_{\mathrm{T}} - ( F_{\mathrm{J}}+ F_g +F_{g1} ) =0 \\ 370 -F_{\mathrm{J}} -30-40=0 \Rightarrow F_{\mathrm{J}}=300\mathrm{N} \end{gathered}$$

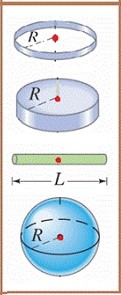
مركز الكتلة Centre of Mass 

يعرف مركز الكتلة  (CM)أنه؛ النقطة التي يمكن افتراض كتلة الجسم كاملة مركزة فيها.

وقد يقع مركز الكتلة داخل الجسم أو خارجه، اعتمادا على شكل الجسم. 

فكيف أحدد موقعه؟ 

 مركز الكتلة  لجسم متماثل منتظم توزيع الكتلة:  

ينطبق موقع مركز كتلة أي جسم متماثل منتظم توزيع الكتلة (متجانس) على 

 مركزه الهندسي. فمثلا ؛ يقع مركز كتلة قضيب فلزي منتظم داخله، وفي منتصف

 المسافة بين نهايتيه. ويقع مركز كتلة مسطرة، أو اسطوانة، أو كرة، أو مكعب في

المركز الهندسي لكل منها. 

المسافة بين نهايتيه.  الشكل المجاور أن مركز الكرة لحلقة دائرية  يقع عند مركزها ا

لهندسي بالرغم من عدم وجود مادة الحلقة عند تلك النقطة، وبالمثل فإن مركز كتلة

   كرة مجوفة يقع في مركزها بالرغم من عدم وجود مادة الحلقة عند تلك النقطة.

  ينطبق موقع مركز الكتلة لجسم 

  متماثل متجانس  على مركزه الهندسي.

حلقة دائرية 

قرص مصمت أو مجوف 

اسطوانة 

كرة مصمتة أو مجوفة 

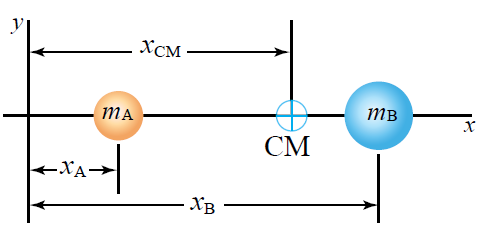
مركز الكتلة لنظام يتألف من جسمين

عندما يتكون النظام من جسمين متساويين في الكتلة، فإن مركز الكتلة للنظام يقع    

عند منتصف المسافة بينهما. فمثلا، يحمل رافع  الاثقال المبين في الشكل ثقلين  

متساويين متصلين بقضيب فلزي، فيكون مركز كتلة الثقلين عند منتصف

المسافة بينهما.أما النظام المكون من جسمين مختلفين في الكتلة؛ فإن مركز  

كتلة النظام يقععلى الخط الواصل بينهما ويكون أقرب إلى الجسم الأكبر كتلة.

يبين الشكل المجاور نظاما يتكون من جسيمين كتلتيهما $\left( {}_{\mathrm{B}}m,{}_{\mathrm{A}}m\right)$يتصلان معا

بقضيب فلزي خفيف مهمل الكتلة. لحساب مركز الكتلة لهذا النظام نختار

نظام محاور يقع فيه الجسيمان على محور  $\left(x\right)$ عند موقعين $\left({}_{\mathrm{B}}x,{}_{\mathrm{A}}x\right)$، ولتحديد

الاحداثي $\left(x\right)$ لموقع مركز كتلة النظام $\left( {}_{\mathrm{CM}}x\right)$ نستخدم العلاقة : 

$\frac{{}_{\mathbf{B}\mathbf{ }}\mathit{x}\mathbf{ }{}_{\mathbf{B}}\mathit{m}\mathbf{+}{}_{\mathbf{A}}\mathit{x}{}_{\mathbf{A}}\mathit{m}}{{}_{\mathbf{B}\mathbf{ }}\mathit{m}\mathbf{ }\mathbf{+}{}_{\mathbf{A}}\mathit{m}}\mathbf{=}\mathbf{ }{}_{\mathbf{M}\mathbf{C}}\mathit{x}$                                           

  مركز الكتلة لجسم غير منتظم الشكل 

يكون مركز الكتلة لجسم غير منتظم الشكل أقرب إلى المنطقة ذات الكتلة الأكبر .

ويمكن تحديد موقع الكتلة للجسم عمليا.  

مركز الكتلة لثقلين متساويين متصلين

بقضيب فلزي، يقع عند منتصف 

 المسافة بينهما.  

 مركز الكتلة لنظام يتكون من جسمين

 مختلفين في الكتلة يقع على الخط 

 الواصل بينهما، و يكون أقرب إلى 

 الجسم ذو الكتلة الأكبر. 

أتحقق (صفحة 50 في الكتاب) 

أين يقع مركز كتلة جسم منتظم متماثل؟ وأين يقع مركز كتلة جسم غير منتظم الشكل؟

 مركز كتلة الجسم المنتظم والمتماثل يقع في مركزه الهندسي، أما الجسم غير المنتظم وغير

المتماثل فيكون مركز كتلته أقرب إلى الجزء ذو الكتلة  الأكبر منه.

المثال (5) (صفحة 50 في الكتاب) 

نظام يتكون من كرتين$\left(m_{\mathrm{B}}= 3.0 kg ) و ( m_{\mathrm{A}} =1.0 kg \right)$،  

إذا علمت أن$( x_{\mathrm{B}}= 15.0 cm)و( x_{\mathrm{A}}=5.0 cm )$.أحدد موقع مركز كتلة النظام. 

المعطيات: 

$\mathrm{cm} 0.15={}_{\mathrm{B}}\mathrm{x} ,\mathrm{cm} 0.5={}_{\mathrm{A}}x, \mathrm{kg} 0.3={}_{\mathrm{B}}m, \mathrm{kg} 0.1={}_{\mathrm{A}}m$

المطلوب :                                                     $(? ={}_{\mathrm{M} \mathrm{C}} x )$

الحل:

أستخدم العلاقة الآتية: 

 $\frac{{}_{\mathrm{B}}x {}_{\mathrm{B}}m+ {}_{\mathrm{A}}x {}_{\mathrm{A}}m}{{}_{\mathrm{B}}m +{}_{\mathrm{A}}m}= {}_{\mathrm{M} \mathrm{C}} x$  

$\frac{ {}^{2-} 10\times 50}{4}= \frac{ {}^{2-} 10 \times 15\times 3+ {}^{2-} 10\times 5\times 1}{ 3+1}=$           

$\mathrm{cm} 5.12 =\mathrm{m} {}^{2-} 10\times 5 .12=$ 

ألا حظ أن موقع  مركز  الكتلة أقرب للكتلة الأكبر                                                         

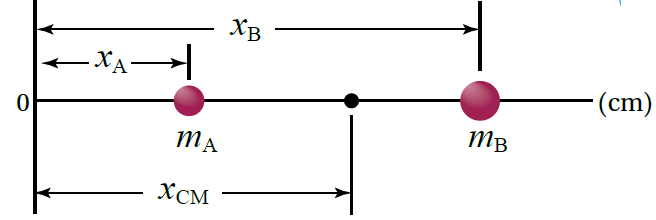تمرين (صفحة 50 في الكتاب)

أعيد حل المثال السابق إذا كانت  $\left( g\mathrm{k} 0.4= {}_{\mathrm{B}}m={}_{\mathrm{A}}m\right)$

الحل:

بما أن الكرتين متساويتين في الكتلة فإن مركز الكتلة في منتصف المسافة بينهما. 

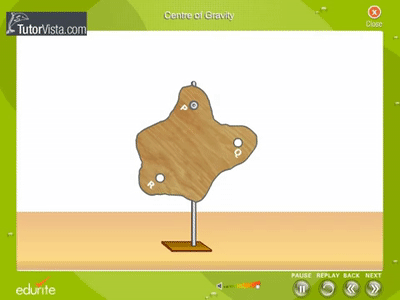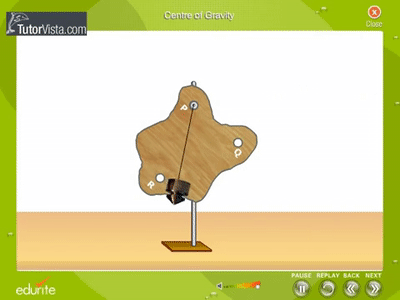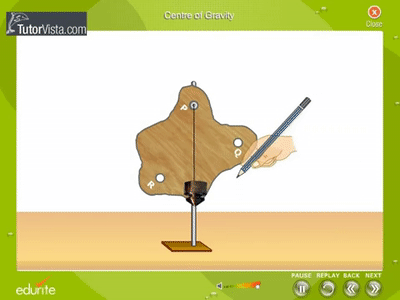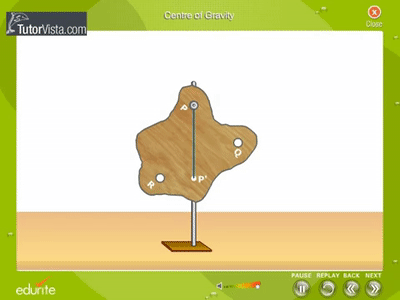
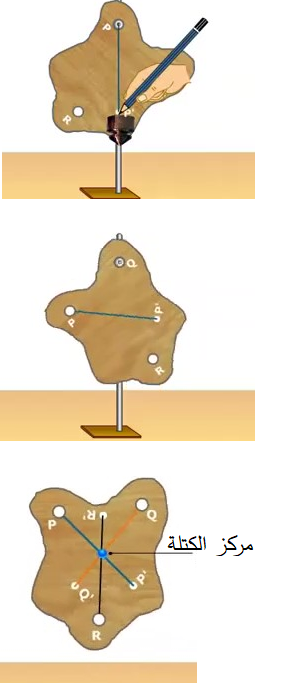
التجربة (1) : تحديد   مركز الكتلة  

الهدف من التجربة: تحديد مركز الكتلة لكل من جسم منتظم الشكل،  

وجسم غير منتظم الشكل.  

الجزء الأول: تحديد مركز الكتلة لمسطرة مترية 

عند تعليق مسطرة بخطاف، فإنها تتزن بوضع أفقي عند تعليقها من  

نقطة منتصف المسافة بين نهايتها (مركزها الهندسي). وهذه النقطة 

هي مركز كتلةالمسطرة (CM). 

الجزء الثاني : تحديد مركز الكتلة لقطعة ورق مقوى غير منتظمة الشكل

نقص قطعة الورق بشكل غير منتظم  ، ونحدث عند حافتها ثقوبا عدة 

 (ثقبين أو ثلاثة)، ونعلق المسطرة من أحد الثقوب في الحامل الرأسي،  

ثم نعلق خيط الشاقول، وننتظر إلى أن يتوقف عن التأرجح، ونرسم خطا 

رأسيا على امتداد خط الشاقول. ونكرر العملية السابقة بتعليق قطعة 

الورق من الثقب الثاني، ثم الثالث. وأحدد نقطة تقاطع الخطوط، حيث  

تمثل هذه النقطة مركز الكتلة للقطعة. 

تتزن المسطرة عند تعليقها من منتصف

المسافة بين  نهايتيها.

الاستنتاج والتحليل لنتائج التجربة:

1. تتزن المسطرة عند نقطة منتصفها (المركز الهندسي)، وهذه النقطة 

هي مركز كتلة المسطرة(CM). فنستنتج أن الأجسام المتماثلة متجانسة

الكتلة تقع مراكز كتلها في مراكزها الهندسية.

2.لتحديد مركز كتلة جسم غير منتظم يلزم تعليقه بشكل حر، من موقعين 

على الأقل، فيكون مركز الكتلة (CM) عند نقطة تقاطع الخطين. 

3. تقع مراكز كتل الأجسام المنتظمة والمتماثلة مثل المسطرة المترية،

في مراكزها الهندسية. أما الاجسام غير المتماثلة وغير المنتظمة مثل 

 قطعة الورق المقوى، فتكون مراكز كتلها أقرب للجزء الأكبر كتلة منها.

4. عند تعليق قطعة الورق المقوّى من نقطة تقاطع الخطوط، فإنها 

لا تدور؛إذ تمثّل هذه النقطة مركز كتلتها، وعند تعليق جسم من مركز

كتلته فإنه يكون متزنًا.

مما سبق نستنتج: مركز الكتلة لجسم منتظم يقع في مركزه الهندسي، 

أما مركز  الكتلة لجسم غير منتظم فيكون أقرب إلى الجزء الأكبر كتلة منه. 

وعند تعليق جسم من مركز كتلته فإنه يكون متزنا؛ لأن  العزم المحصل  

المؤثر فيه يساوي صفر. 

سؤال 

نظام يتكون من كرتين كتلتيهما $\left(m\right) و \left(m6\right)$ تتصلان بقضيب خفيف كتلته مهملة،

 والمسافة بين مركزيهما $\left(d\right)$، كما يبين الشكل المجاور. أحدد على القضيب 

 الواصل بين الكرتين موقع نقطة التعليق التي يكون عندها النظام متزنا.

الحل: 

يكون النظام متزنا عند تعليقه من موقع مركز الكتله. ولتحديد مركز كتلة النظام،

 نرسم محور ($x$) بحيث تقع الكرة الأولى ($m6$) عند نقطة الأصل $\left( 0={}_{1}x\right)$، فيكون

 بعد الكرة الثانية عن نقطة الأصل ($d={}_{2}x$)، ونفترض أن نقطة مركز الكتلة

($\mathrm{CM}$) على بعد (${}_{\mathrm{M} \mathrm{C} }x$) من نقطة الأصل. ونطبق العلاقة : 

 $\frac{ d\times m}{ m7}= \frac{ d\times m+ 0\times m6}{ m+m6}= \frac{{}_{2}x {}_{2}m +{}_{1}x {}_{1}m}{ {}_{2}m+{}_{1}m}= {}_{\mathrm{M} \mathrm{C}}x$ 

$\frac{d}{7}={}_{ \mathrm{CM}}x$ 

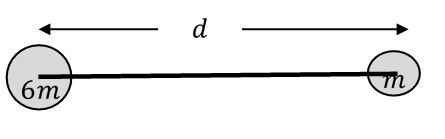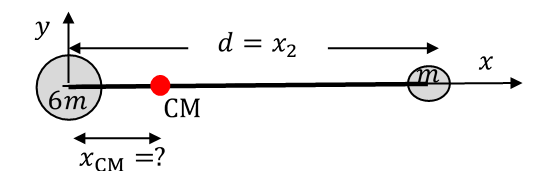أفكر  (صفحة 48 في الكتاب) 

يكون العزم المحصل لجزيئات نظام حول مركز كتلته يساوي صفرا. كيف  

يمكن استخدام هذه الطريقة لتحديد الاحداثي $\left(x_{\mathrm{CM}}\right)$ لمركز كتلة النظام

 الموضح في الشكل؟

الحل: 

$$\begin{gathered} \sum {\tau }_{\mathrm{CM}}=0 \Rightarrow m_{A}g (x_{\mathrm{CM}}- x_{\mathrm{A}}) - m_{\mathit{A}}g (x_B- x_{\mathrm{CM}})=0 \\ {m}_{\mathrm{A}}(x_{\mathrm{CM}}- x_{\mathrm{A}}) - m_{\mathrm{B}} (x_{\mathrm{B}} - x_{\mathrm{CM}}) =0 \\ m_{\mathrm{A}}{x}_{\mathrm{CM}}-m_{\mathrm{A}} x_{\mathrm{A}} - m_{\mathrm{B}} x_{\mathrm{B}} +m_{\mathrm{B}} x_{\mathrm{CM}}=0 \\ {x}_{\mathrm{CM}}(m_{\mathrm{A}}+m_{\mathrm{b}})=m_{\mathrm{A}} x_{\mathrm{A}}+m_{\mathrm{B}} x_{\mathrm{B}} \\ {x}_{\mathrm{CM}}=\frac{m_{\mathrm{A} }{x}_{\mathrm{A}}+m_{\mathrm{B}} x_{\mathrm{B}}}{m_{\mathrm{A}}+m_{\mathrm{B}}} \end{gathered}$$