العوامل
الفكرة الرئيسية : إيجاد عوامل عدد كلي .
* العامل : هو أحد الأعداد التي يقبل عدد ما القسمة عليه من دون باقي , ويسمى العاملان اللذان ناتج ضربهما يعطي العدد زوج عوامل العدد .
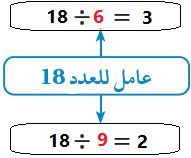
أي أن عوامل العدد : هي الأعداد جميعها التي يقبل العدد القسمة عليها من دون باقي .
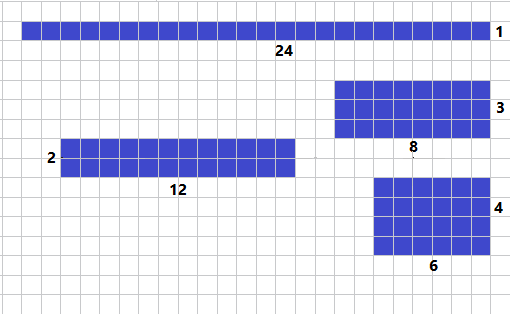
مثال 1 : استعمل الشبكات لإيجاد عوامل العدد 24 .
الجواب :
لإيجاد عوامل العدد 24 , أرسم على الشبكة الخيارات الممكنة جميعها لعددين ناتج ضربهما يساوي 24 , بحيث يشير الصف في كل شكل إلى عامل والعمود إلى عامل آخر .
 |
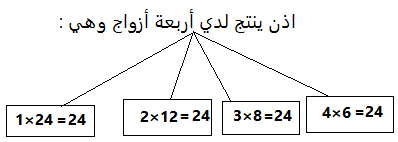 |
أي أن عوامل العدد 24 هي : 1 , 2 , 3 , 4 , 6 , 8, 12 , 24 وهي تشكل أربعة أزواج ناتج ضرب كل منها يساوي 24 .
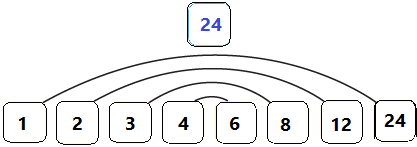
ويمكنني استعمال قواعد قابلية القسمة , لأجد عوامل عدد .
فمثلا : العدد الكلي الذي يقبل القسمة على 2 , يكون أحد عوامله 2 . والعدد الكلي الذي يقبل القسمة على 3 يكون أحد عوامله 3 , والعدد الكلي الذي آحاده
0 أو 5 يكون أحد عوامله 5 وهكذا .....
مثال 2 : جد عوامل العدد 45 جميعها .
الجواب :
باستعمال قواعد قابلية القسمة فإن :
العدد 45 يقبل القسمة على 3 وناتج القسمة 15 , لذا فإن العددين 3 و 15 عاملين للعدد 45 .
العدد 45 يقبل القسمة على 5 وناتج القسمة 9 , لذا فإن العددين 5 و 9 عاملين للعدد 45 .
إذن عوامل العدد 45 هي : 1 , 3 , 5 , 9 , 15 , 45 .
مثال 3 : في نشاط لمادة العلوم صمم طارق نموذجا لمزرعة رياح , ويريد توزيع 50 مروحة بشكل متساو في صفوف داخل النموذج , كم عدد الصفوف التي يمكن لطارق أن يرتب المراوح بشكل متساو فيها ؟ كم عدد المراوح في كل صف :
الجواب :
لإيجاد العدد الممكن للصفوف , أجد عوامل العدد 50 باستعمال قواعد قابلية القسمة :
العدد 50 يقبل القسمة على 2 وناتج القسمة 25 . لذا فإن العددين 2 و 25 عاملين للعدد 50 .
العدد 50 يقبل القسمة على 5 وناتج القسمة هو 10 , لذا فإن العددين 5 و 10 عاملين للعدد 50 .
إذن عوامل العدد 50 هي : 1 , 2 , 5 , 10 , 25 , 50
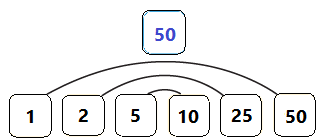
وبالنظر إلى أزواج العوامل بالشكل أعلاه , يمكن لطارق أن يرتب المراوح كما يأتي :
- صفان في كل منهما 25 مروحة , أو 25 صف في كل منها مروحتان .
- 5 صفوف في كل منها 10 مراوح , أو 10 صفوف في كل منها 5 مراوح .
- صف واحد فيه 50 مروحة .