القطعُ المُتوسِّطةُ والارتفاعاتُ في المُثلَّثِ
Medians and Altitudes in Triangle
فكرةُ الدرسِ : • تعرُّفُ نظريةِ مركزِ المُثلَّثِ، واستعمالُها لإيجادِ قياساتٍ مجهولةٍ.
• إيجادُ ملتقى ارتفاعاتِ المُثلَّثِ في المستوى الإحداثيِّ.
أولًا : القطعُ المُتوسِّطةُ في المُثلَّثِ
|
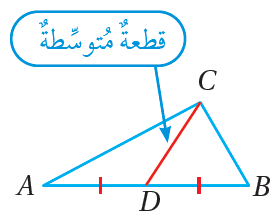
القطعةُ المُتوسِّطةُ للمُثلَّثِ: هيَ القطعةُ المستقيمةُ الواصلةُ بينَ أحدِ رؤوسِ المُثلَّثِ ومنتصفِ الضلعِ المُقابِلِ لهُ. • لكلِّ مُثلَّثٍ ثلاثُ قطعٍ مُتوسِّطةٍ تلتقي في نقطةٍ واحدةٍ تُسمّى مركزَ المُثلَّثِ. |
 |
نظريةٌ (مركزُ المُثلَّثِ)
|
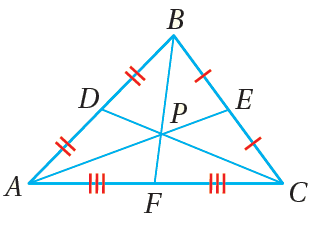
يبعدُ مركزُ المُثلَّثِ عنْ كلٍّ منْ رؤوسِهِ ثلثيْ طولِ القطعةِ المستقيمةِ الواصلةِ بينَ ذلكَ الرأسِ ومنتصفِ الضلعِ المُقابِلِ لهُ. مثالٌ: إذا كانَتِ النقطةُ هيَ مركزَ ، فإنَّ:
|
 |
مثال 1
إذا كانت النقطة D هي مركز ، وكان
فأجد كلّ مما يأتي:
1) طول
2) طول
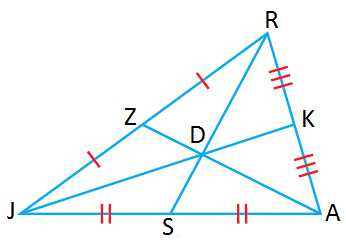
الحل:
1)
2)
•• يُمكِنُ إيجادُ مركزِ أيِّ مُثلَّثٍ في المستوى الإحداثيِّ إذا عُلِمَتْ إحداثياتُ رؤوسِهِ.
مثال 2
يظهرُ المُثلَّثُ ΔABC في المستوى الإحداثيِّ المُجاوِرِ.
أجدُ إحداثييْ مركزِ هذا المُثلَّثِ.
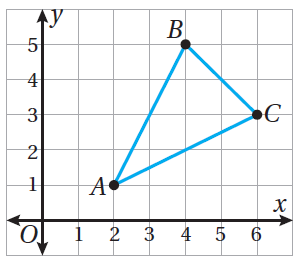
الحل:
الخطوةُ 1: أجدُ نقطةَ منتصفِ أحدِ أضلاعِ المُثلَّثِ.
أستعملُ صيغةَ نقطةِ المنتصفِ لإيجادِ منتصفِ ، ولتكنْ :
الخطوةُ 2 : أجدُ مركزَ المُثلَّثِ.
• أُعيِّنُ النقطةَ D في المستوى الإحداثيِّ، ثمَّ أرسمُ DB
· أُلاحِظُ أنَّ DB رأسيةٌ، وأنَّهُ يُمكِنُ إيجادُ طولِها على النحوِ الآتي:
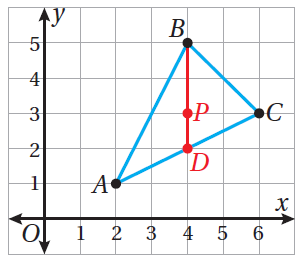
صيغةُ طولِ قطعةٍ مستقيمةٍ رأسيةٍ
بالتعويضِ:
بالتبسيطِ، وإيجادِ القيمةِ المُطلَقةِ
إذنْ، طولُ هوَ 3 وحداتٍ.
• أفترضُ أنَّ النقطةَ هيَ مركزُ . ومنْ ثَمَّ، فإنَّ ؛ لذا يقعُ المركزُ على بُعْدِ وحدةٍ أسفلَ الرأسِ
إذنْ، إحداثيّا مركزِ هذا المُثلَّثِ (إحداثيّا النقطةِ ) هما: .
•• أتعلَّمُ : يُمكِنُ التحقُّقُ منْ صحَّةِ الحَلِّ باستعمالِ قطعةٍ مُتوسِّطةٍ أُخرى لإيجادِ مركزِ المُثلَّثِ.
ثانيًا: ارتفاعاتُ المُثلَّثِ
ارتفاعُ المُثلَّثِ : هوَ القطعةُ المستقيمةُ العموديةُ النازلةُ منْ أحدِ رؤوسِ المُثلَّثِ إلى الضلعِ المُقابِلِ لها، أوْ إلى المستقيمِ الذي يحوي الضلعَ المُقابِلَ لها.
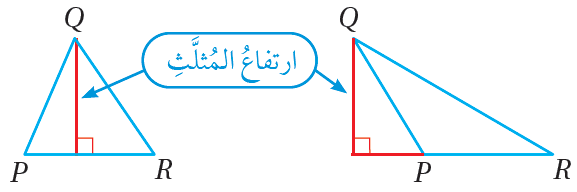
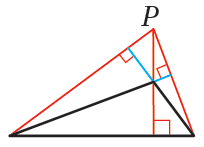
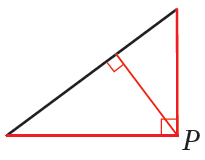
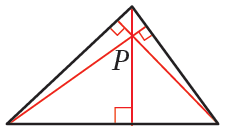
•• لكلِّ مُثلَّثٍ ثلاثةُ ارتفاعاتٍ تتقاطعُ في نقطةٍ مُشترَكةٍ تُسمّى ملتقى الارتفاعاتِ ويعتمدُ موقعُها على نوعِ المُثلَّثِ كما في الأشكالِ الآتيةِ:
 |
 |
 |
|
مُثلَّثٌ مُنفرِجُ الزاويةِ، وفيهِ تقعُ خارجَ المُثلَّثِ. |
مُثلَّثٌ قائمُ الزاويةِ، وفيهِ |
مُثلَّثٌ حادُّ الزوايا، وفيهِ تقعُ داخلَ المُثلَّثِ. |
مثال 3
إذا كانَتْ: ( 5 , K(0, 0), M(3, 12), L(10 ، فأجدُ إحداثييْ ملتقى ارتفاعاتِ رؤوسِ ΔKLM
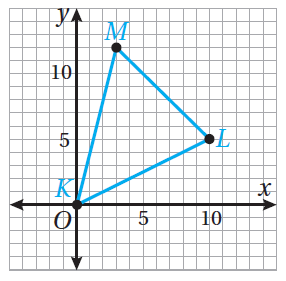
الحل:
الخطوةُ 1: أُمثِّلُ ΔKLM بيانيًّا.
الخطوةُ 2: أجدُ ميليْ ضلعينِ منْ أضلاعِ المُثلَّثِ.
الخطوةُ 3: أجدُ معادلةَ الارتفاعِ العموديِّ على كلٍّ منَ الضلعينِ اللذينِ اخترْتُهُما في الخطوةِ السابقةِ.
• معادلةُ الارتفاعِ العموديِّ على
بالتعويضِ:
أتعلم : الرأسُ M هوَ الرأسُ المُقابِلُ ل KL ؛ لذا يقعُ على الارتفاعِ العموديِّ على KL
ميلُ الارتفاعِ العموديِّ على KL يساوي سالبَ مقلوبِ ميلِ KL ؛ أيْ إنَّهُ يساوي 2-
• معادلةُ الارتفاعِ العموديِّ على
صيغةُ الميلِ ونقطةٍ:
بالتعويض:
أتعلم: الرأسُ K هوَ الرأسُ المُقابِلُ ل LM ؛ لذا يقعُ على الارتفاعِ العموديِّ على LM
ميلُ الارتفاعِ العموديِّ على LM يساوي سالبَ مقلوبِ ميلِ LM ؛ أيْ إنَّهُ يساوي 1
الخطوةُ 4 : أحُلُّ نظامَ المعادلتينِ الناتجَ لإيجادِ إحداثييْ ملتقى الارتفاعاتِ.
بما أنَّ المعادلةَ الثانيةَ مكتوبةٌ بالنسبةِ إلى y ، فإنَّني أُعوِّضُ x بدلًا منْ y في المعادلةِ الأولى :
| المعادلةُ الأولى | |
| بالتعويضِ عن y بـ x | |
| بجمعِ 2x لطرفيِ المعادلةِ | |
| بقسمةِ طرفيِ المعادلةِ على 3 |
بما أنَّ x = 6 ، فإنَّ y = 6 ، وذلكَ بتعويضِ قيمةِ x في أيٍّ منَ المعادلتينِ.
إذنْ، إحداثيّا ملتقى ارتفاعاتِ رؤوسِ ΔKLM هما : (6 , 6).
مُلخَّصُ المفهومِ (قطعٌ مستقيمةٌ ونقاطٌ خاصةٌ في المُثلَّثِ)
| المُنصِّفاتُ العموديةُ | مُنصِّفاتُ الزوايا | القطعُ المُتوسِّطةُ | الارتفاعاتُ | القطعُ الخاصةُ: |
| مركزُ الدائرةِ الخارجيةِ للمُثلَّثِ. |
مركزُ الدائرةِ الداخليةِ للمُثلَّثِ. |
مركزُ المُثلَّثِ | ملتقى الارتفاعاتِ. | نقطةُ التلاقي: |
| النقطةُ P مركزُ الدائرةِ الخارجيةِ لـ ΔABC وهيَ تقعُ على أبعادٍ متساويةٍ منْ رؤوسِهِ. |
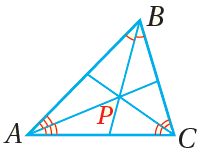
النقطةُ P مركزُ الدائرةِ الداخليةِ لـ ΔABC وهيَ تقعُ على أبعادٍ متساويةٍ منْ أضلاعِهِ. |
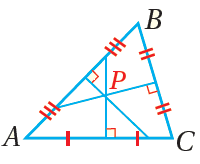
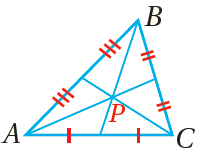
النقطةُ P مركزُ ΔABC ، وهيَ تبعدُ عنْ كلِّ رأسٍ ثلثيْ طولِ القطعةِ الواصلةِ بينَ ذلكَ الرأسِ ومنتصفِ الضلعِ المُقابِلِ لهُ. |
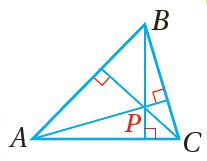
النقطةُ P هيَ ملتقى ارتفاعاتِ ΔABC |
الخاصيةُ: |
 |
 |
 |
 |
مثالٌ: |