أجد القِيّم القصوى المحلية والقِيّم القصوى المُطلّقة (إِن وُجدت) للاقتران المعطى تمثيله البياني في كل مما يأتي:
الحل:


أجد القيمة العظمى المُطلّقة والقيمة الصغرى المُطلّقة (إِنْ وُجدت) لكل اقتران ممّا يأتي في الفترة المعطاة:
ويمكن الاستعانة بما يعرف باختبار المشتقة الاولى والثانية
والتي ستتعرف عليها لاحقا لتحديد القيم القصوى .
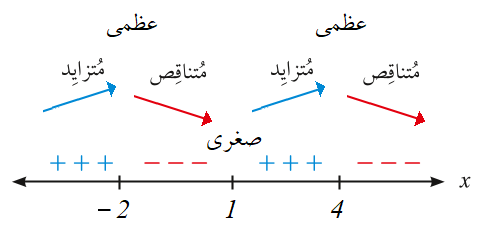
قيم الحرجة هي بحيث :
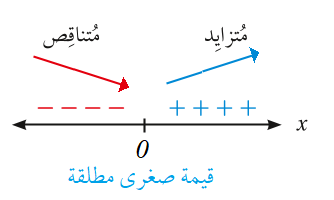
قيمة صغرى مطلقة
لا توجد قيمة قصوى محلية عندها
قيمة عظمى مطلقة

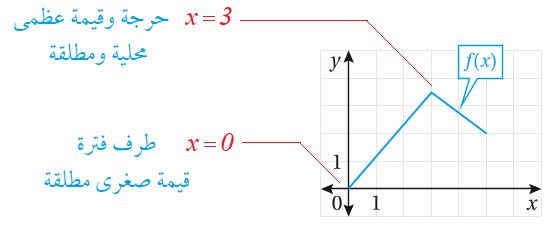
أجد القيّم القصوى المحلية (إنْ وُجدت) للاقتران:
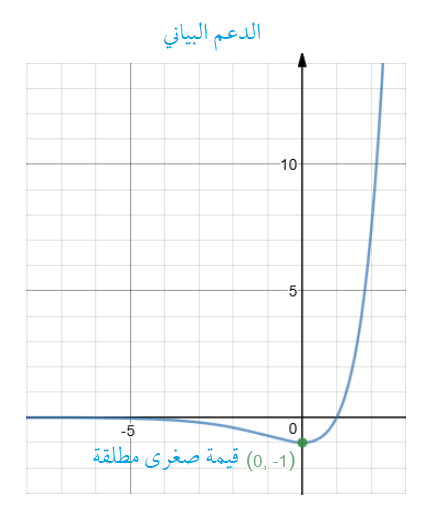
يوجد قيمة صغرى محلية مطلقة هي والشكل المجاور يوضح ذلك .

أجد القيمة العظمى المُطلّقة والقيمة الصغرى المُطلّقة (إِنْ وُجدت) للاقتران:
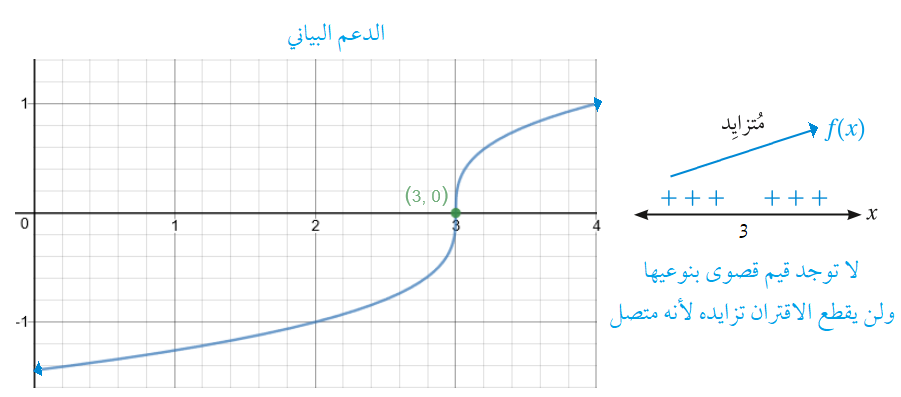 يوجد عند قيمة حرجة لأن غير موجودة .
يوجد عند قيمة حرجة لأن غير موجودة .

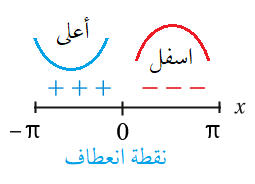
أجد فترات التقعر للأعلى وللأسفل ونقاط الانعطاف (إِنْ وُجدت) لمنحنى كل اقتران مما يأتي:
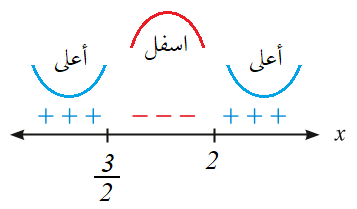 لذلك فإن منحنى الاقتران مقعر لأعلى في الفترة ومقعر لأسفل في الفترة
لذلك فإن منحنى الاقتران مقعر لأعلى في الفترة ومقعر لأسفل في الفترة
ونقاط الانعطاف هي :

وهذه المعادلة لا يوجد لها حل بالتالي فلا توجد نقطة إنعطاف
وسنبحث في إشارة المشتقة الثانية حول العدد (1) جذر المقام
ولا توجد نقطة انعطاف عند x=1 لانه غير معرّف عندها

إذا كان: فأستعمل اختبار المشتقة الثانية لإيجاد القِيّم القصوى المحلية للاقتران
إذن يوجد عند قيمة صغرى محلية وهي

يمثل الاقتران موقع جسم يتحرَّك في مسار مستقيم؛ حيث S الموقع بالأمتار و t الزمن بالثواني:
a) ما الفترات الزمنية التي يتحرَّك فيها الجسم في الاتجاه الموجب والاتجاه السالب؟
وسنبحث في إشارة المشتقة حول العدد (1) جذر المشتقة :
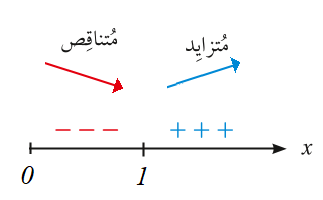 يتحرَّك الجسم في الاتجاه الموجب في الفترة
يتحرَّك الجسم في الاتجاه الموجب في الفترة
وفي الاتجاه السالب في الفترة .
b) ما الفترات التي تتزايد فيها سرعة الجسم ؟ وما الفترات التي تتناقص فيها سرعة الجسم ؟
وسنبحث في إشارة التسارع حول العدد (0) جذر المشتقة :
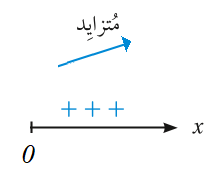
تتزايد السرعة في الفترة

أجد القيم الحرجة والقيم القصوى المحلية والمُطلّقة (إِنْ وُجدت) للاقتران الممثل بيانياً في كل مما يلي:
1
2
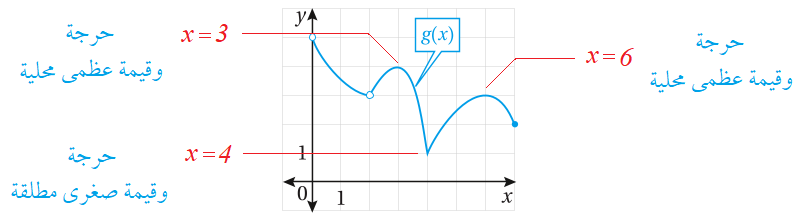
3
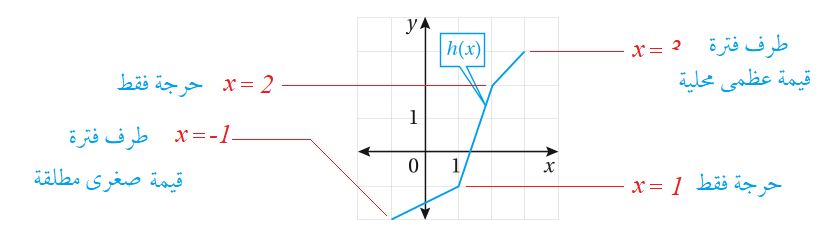
أجد القيمة العظمى المُطلّقة والقيمة الصغرى المُطلقة (إِنْ وُجدت) لكل اقتران مما يأتي في الفترة المعطاة:
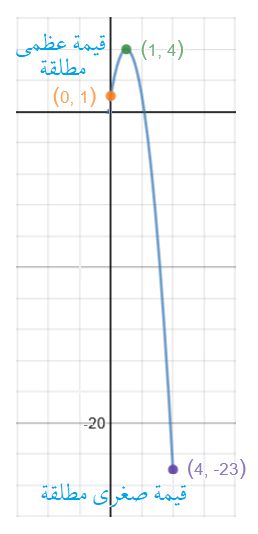
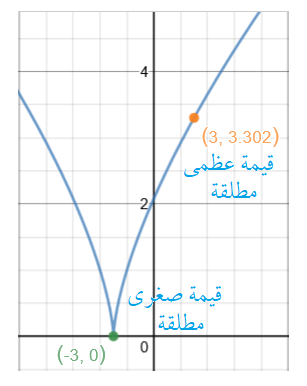
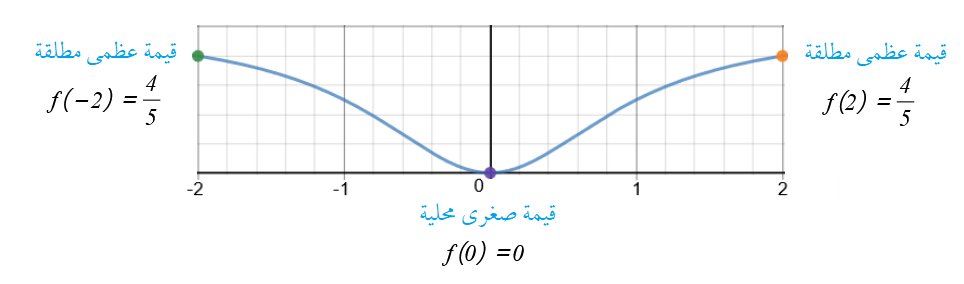
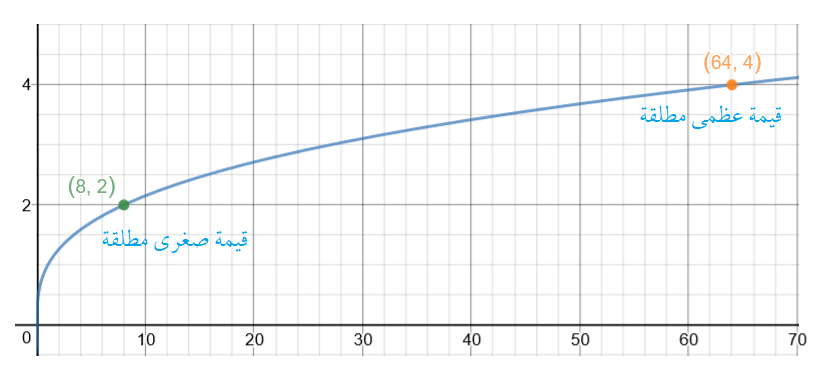
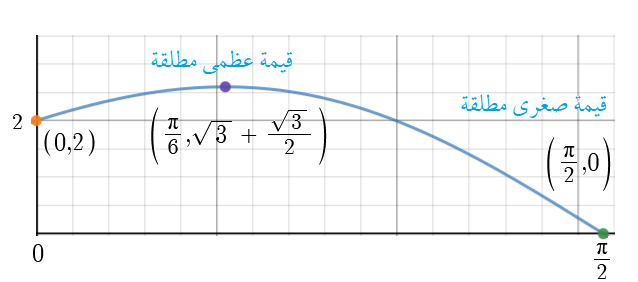

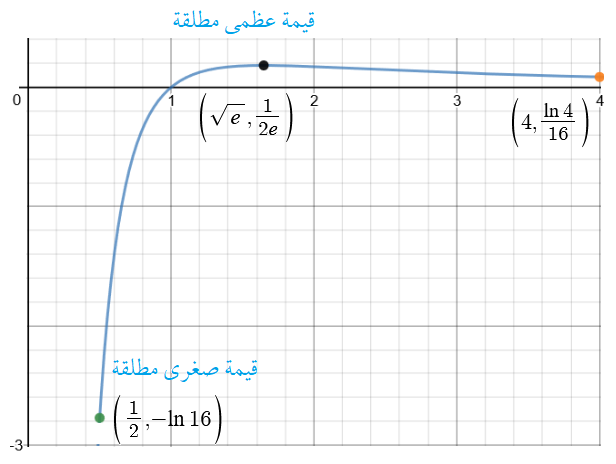
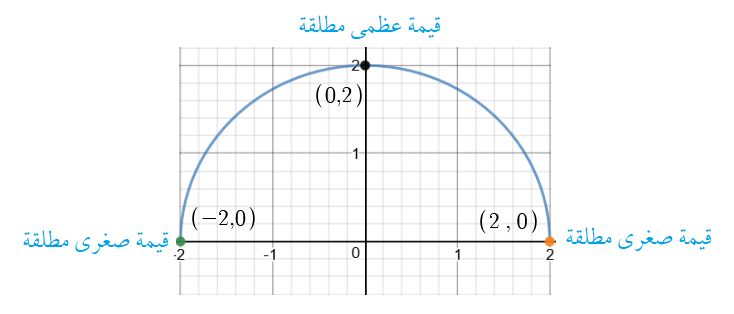
أجد فترات التزايد وفترات التناقص لكل اقتران ممّا يأتي ، ثم أجد القِيّم القصوى المحلية والمُطلقة (إِنْ وُجدت) لكل اقتران ممّا يأتي:
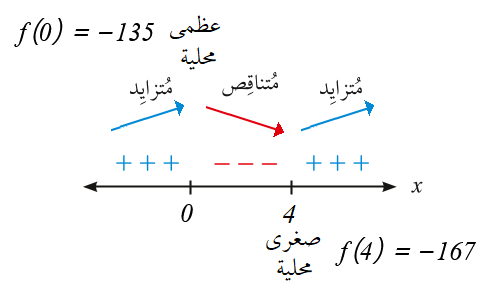
فترات التزايد : وفترات التناقص :
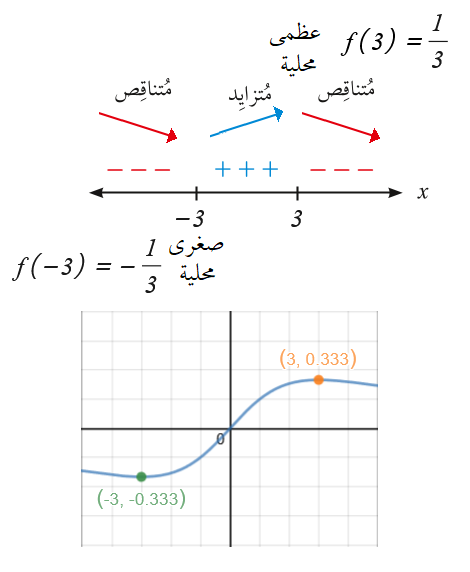
فترات التزايد : وفترات التناقص :
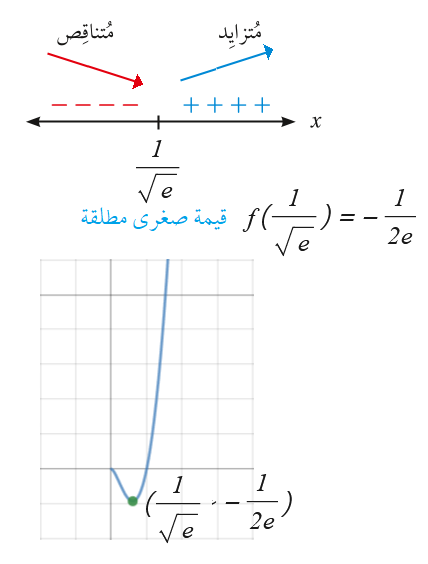
فترات التزايد : ، فترات التناقص :
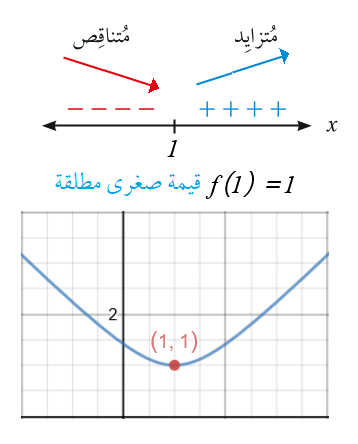
فترات التزايد : , فترات التناقص :
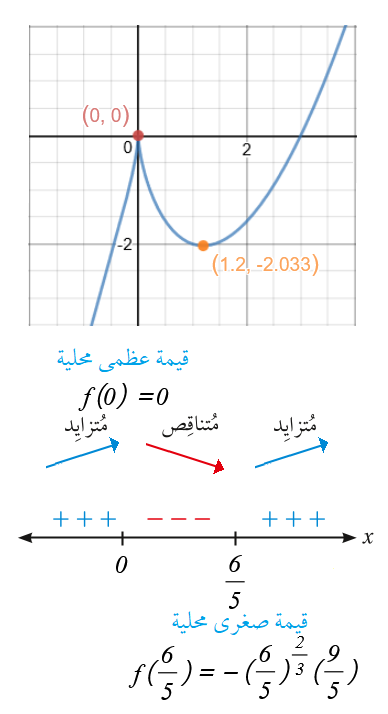
فترات التزايد : ، فترات التناقص :
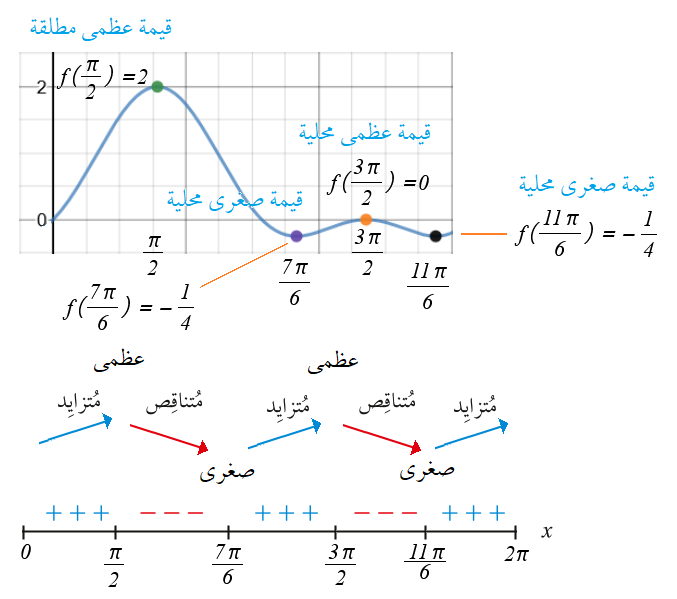
فترات التزايد : , فترات التناقص :
فترات التزايد :
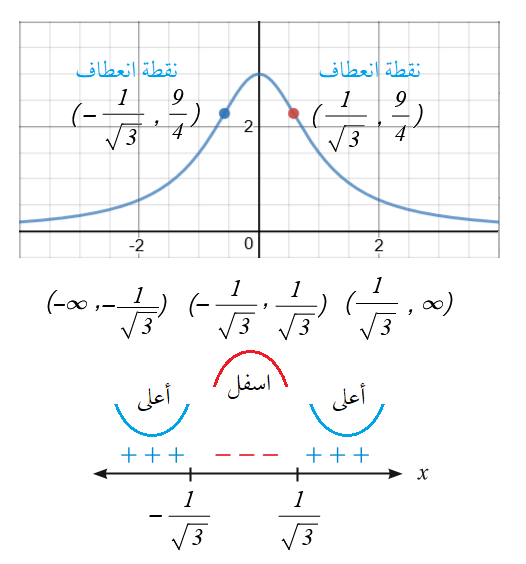
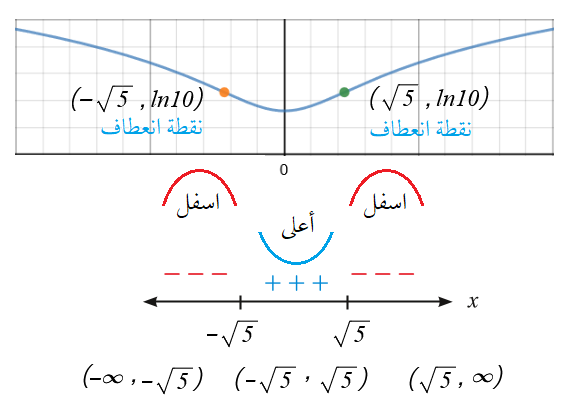
أجد فترات التقعّر للأعلى وللأسفل ونقاط الانعطاف (إنْ وُجدت) لمنحنى كل اقتران ممّا يأتي:
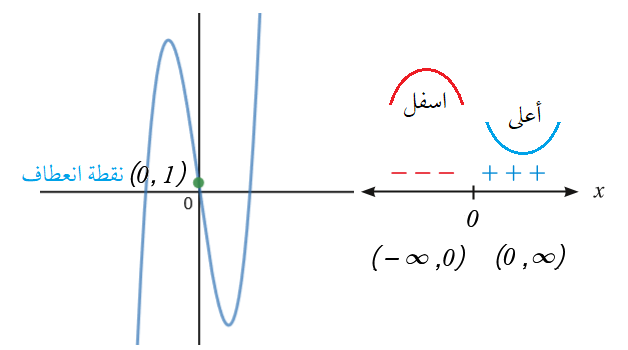
توجد نقاط انعطاف .
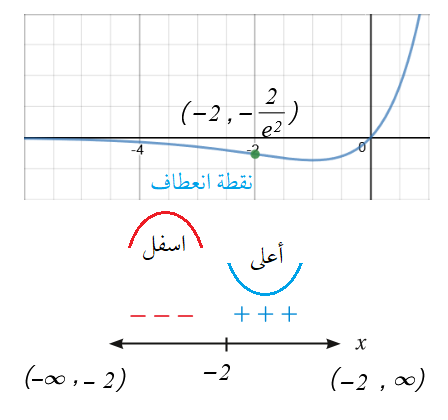
أجد القِيّم القصوى المحلية لكل اقتران مما يأتي ، مُستعملًا اختبار المشتقة الثانية (إنْ أمكن):

فيوجد للاقتران قيمة عظمى محلية مطلقة عند
لا توجد قيم قصوى مطلقة داخل الفترة فقط عند الاطراف
يوجد عند قيمة عظمى مطلقة .و يوجد عند قيمة صغرى مطلقة .
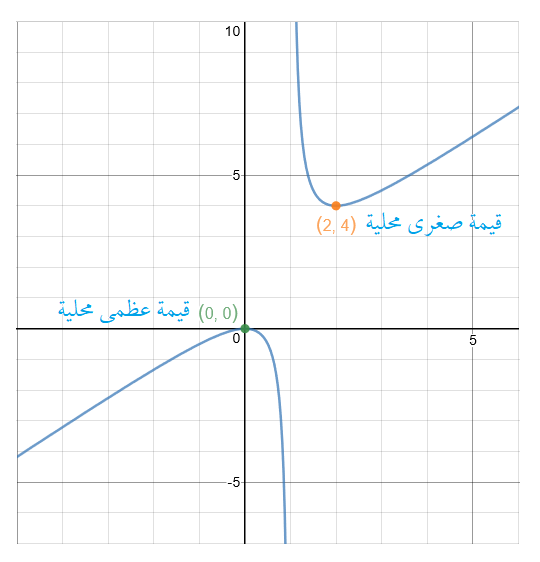
فيوجد للاقتران قيمة عظمى محلية عند ويوجد للاقتران قيمة صغرى محلية عند
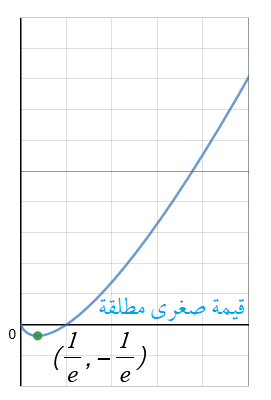
فيوجد للاقتران قيمة صغرى محلية مطلقة عند
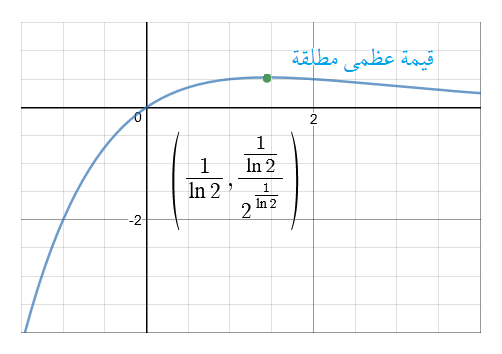
فيوجد للاقتران قيمة عظمى محلية مطلقة عند
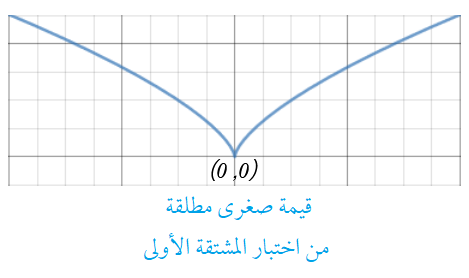
فهو مقعر لاسفل دائما ، ويوجد للاقتران قيمة صغرى محلية مطلقة عند
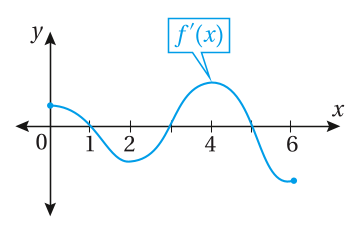
أستعمل التمثيل البياني المجاور لمنحنى لإيجاد كل مما يأتي:
32) قِيَم التي يكون عندها للاقتران قِيّم قصوى محلية ، مبينا نوعها.
الحل: 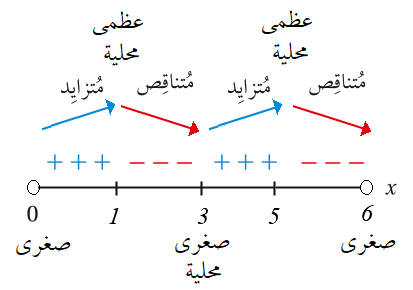
يوجد للاقتران قيمة عظمى محلية عند
يوجد للاقتران قيمة صغرى محلية عند
33) فترات التزايد وفترات التناقص للاقتران .
الحل:
الاقتران متزايد في الفترة :
الاقتران متناقص في الفترة :
34) إذا كان للاقتران: قيمة عظمى محلية عند ، وقيمة صغرى محلية عند النقطة فأجد قيمة كل من الثوابت .
وجود قيمة قصوى لاقتران كثير حدود تعني أن المشتقة عندها تساوي صفراَ .
35) إذا كان للاقتران: نقطة انعطاف عندما فأجد قيمة الثابت .
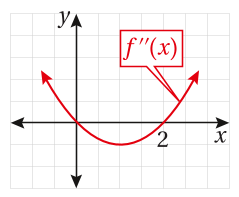 أستعمل التمثيل البياني المجاور لمنحنى لإيجاد كل مما يأتي:
أستعمل التمثيل البياني المجاور لمنحنى لإيجاد كل مما يأتي:
36) فترات التقّعر للأعلى وللأسفل لمنحنى الاقتران .
الاقتران مقعر لأعلى في الفترة لأن
الاقتران مقعر لأسفل في الفترة لأن
37) الإحداثي لنقاط انعطاف منحنى الاقتران .
الحل:
يوجد لمنحنى الاقتران نقطتي إنعطاف عند وذلك لأنه بدّل من إتجاه تقعره حول كل منهما .
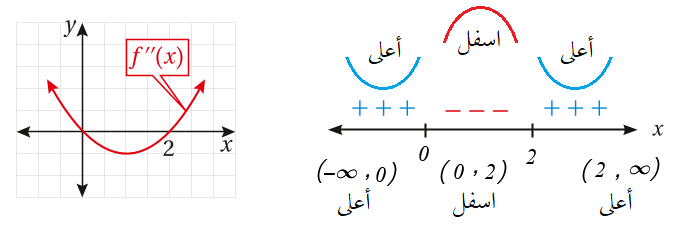
.
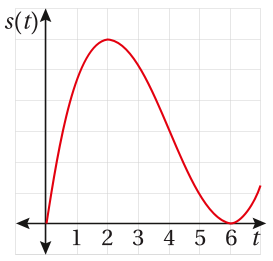
يمثل الاقتران الُمبيّن منحناه في الشكل المجاور
موقع جسم يتحرَّك في مسار مستقيم ،
حيث S الموقع بالأمتار و t الزمن بالثواني:
38) أجد قِيَم t التي يكون عندها الجسم في حالة سكون.
الحل:
سيكون الجسم في حالة سكون عندما تصبح سرعته المتجهة تساوي صفراً .
أي عندما ويوجد لمنحنى الاقتران مماساً أفقياً .
39) ما الفترات الزمنية التي يتحرّك فيها الجسم في الاتجاه الموجب والاتجاه السالب؟
الحل:
يتحرك الجسيم في الإتجاه الموجب في الفترة لأنَّ الاقتران في حالة تزايد ومشتقته موجبة .
يتحرك الجسيم في الإتجاه السالب في الفترة لأنَّ الاقتران في حالة تناقص ومشتقته سالبة
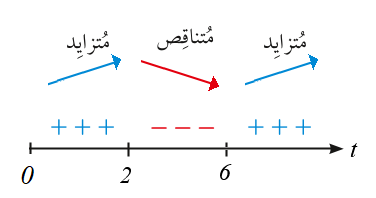
40) إذا كان تسارع الجسم صفرًا عندما فما الفترات التي تتزايد فيها سرعة الجسم المتجهة؟ وما الفترات التي تتناقص فيها سرعة الجسم المتجهة؟
الحل:
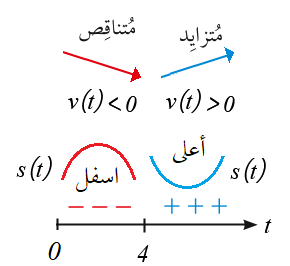 بما أن الاقتران مقعر لاسفل في الفترة مما يعني :
بما أن الاقتران مقعر لاسفل في الفترة مما يعني :
أنَّ المشتقة الثانية سالبة والمشتقة الأولى في حالة تناقص
أي أن السرعة المتجهة متناقصة في الفترة التي يكون فيها الاقتران مقعر لأسفل .
وكذلك بما أن الاقتران مقعر لاعلى في الفترة مما يعني:
أنَّ المشتقة الثانية موجبة والمشتقة الأولى في حالة تزايد
أي أن السرعة المتجهة متزايدة في الفترة التي يكون فيها الاقتران مقعر لأعلى .
41) مُكبّرات صوت:يُمثُل الاقتران الربح الأسبوعي (بالدينار) لأحد المصانع من إنتاجه حيث x عدد مكبرات الصوت المبيعة .
أجد عدد مُكبّرات الصوت الذي يُحقْقَ أكبر ربح مُمكن.
الحل:
سيُحقْقَ أكبر ربح مُمكن عند قيم التي يوجد عندها قيمة عظمى مطلقة .
سنجري أختبار المشتقة الأولى حول العدد
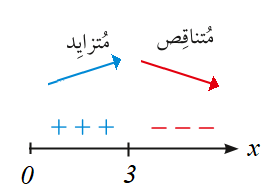
يوجد لمنحنى الاقتران قيمة عظمى مطلقة عند تجعل الربح أكبر ما يمكن .
يمُثلُ الاقتران موقع جسم يتحرَّك في مسار مستقيم ، حيث S الموقع بالأمتار ، وt الزمن بالثواني:
42) ما الفترات الزمنية التي يتحرَّك فيها الجسم في الاتجاه الموجب والاتجاه السالب؟
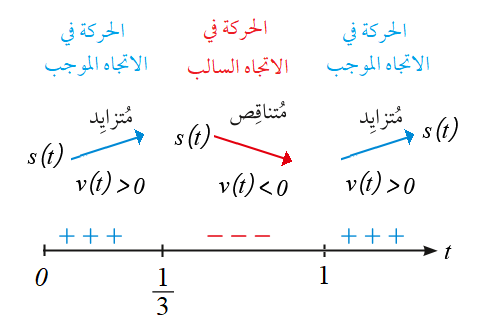 يتحرك الجسيم في الإتجاه الموجب في الفترة
يتحرك الجسيم في الإتجاه الموجب في الفترة
لأنَّ الاقتران في حالة تزايد ومشتقته موجبة .
يتحرك الجسيم في الإتجاه السالب في الفترة
لأنَّ الاقتران في حالة تناقص ومشتقته سالبة .
43) ما الفترات التي تتزايد فيها سرعة الجسم ؟ وما الفترات التي تتناقص فيها سرعة الجسم ؟
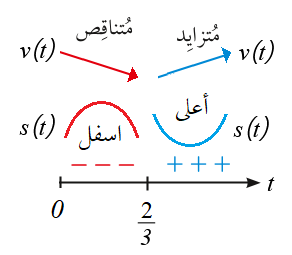 بما أن الاقتران مقعر لاسفل في الفترة مما يعني :
بما أن الاقتران مقعر لاسفل في الفترة مما يعني :
أنَّ المشتقة الثانية سالبة والمشتقة الأولى في حالة تناقص
أي أن السرعة المتجهة متناقصة في الفترة التي يكون فيها الاقتران مقعر لأسفل .
وكذلك بما أن الاقتران مقعر لاعلى في الفترة مما يعني:
أنَّ المشتقة الثانية موجبة والمشتقة الأولى في حالة تزايد
أي أن السرعة المتجهة متزايدة في الفترة التي يكون فيها الاقتران مقعر لأعلى .
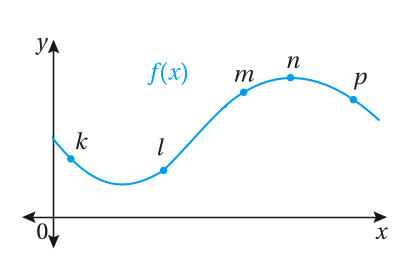 تبرير: يبين الشكل المجاور منحنى الاقتران . أحدَّد النقطة (النقاط) من بين
تبرير: يبين الشكل المجاور منحنى الاقتران . أحدَّد النقطة (النقاط) من بين
مجموعة النقاط : على منحنى الاقتران التي تُحققَ
كلا من الشروط الآتية . مُبرّرًا إجابتي:
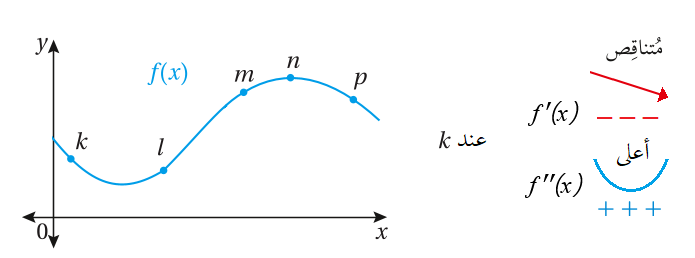
44) أن تكون إشارة كل من و موجبة.
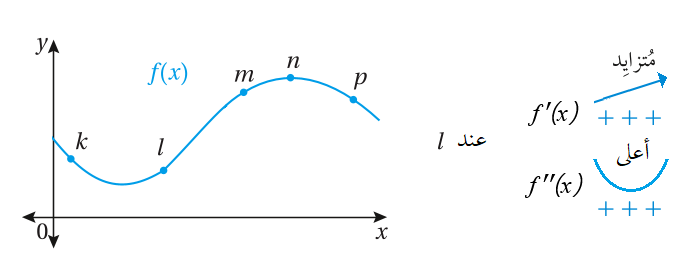
45) أن تكون إشارة كل من و سالبة.
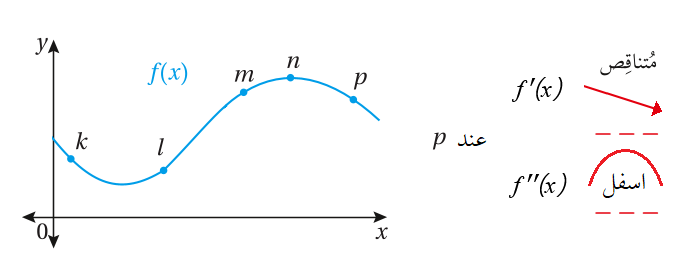
46) أن تكون إشارة سالبة ، وإشارة موجبة.
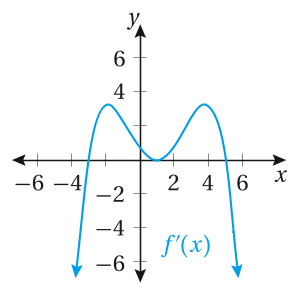 تبرير: أستعمل التمثيل البياني المجاور لمنحنى لإيجاد كل مما يأتي : مبررا إجابتي:
تبرير: أستعمل التمثيل البياني المجاور لمنحنى لإيجاد كل مما يأتي : مبررا إجابتي:
47) قِيّم التي يكون عندها للاقتران قِيّم قصوى محلية مُبيُنًا نوعها.
الحل: 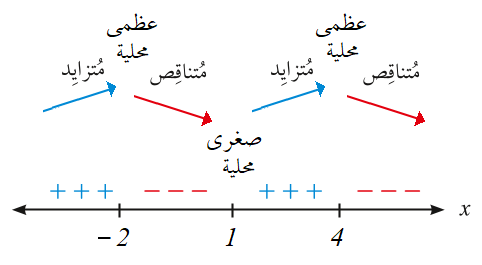
يوجد للاقتران قيمة عظمى محلية عند
يوجد للاقتران قيمة صغرى محلية عند
48) فترات التزايد وفترات التناقص للاقتران .
 الحل:
الحل:
الاقتران متزايد في الفترة :
الاقتران متناقص في الفترة :
49) فترات التقعر للأعلى وللأسفل لمنحنى الاقتران .
 الحل:
الحل:
الاقتران مقعر لاسفل في الفترة :
الاقتران مقعر لاعلى في الفترة :
50) الإحداثي لنقاط الانعطاف.
 الحل:
الحل:
يوجد لمنحنى الاقتران نقطتي إنعطاف عند قيمتي
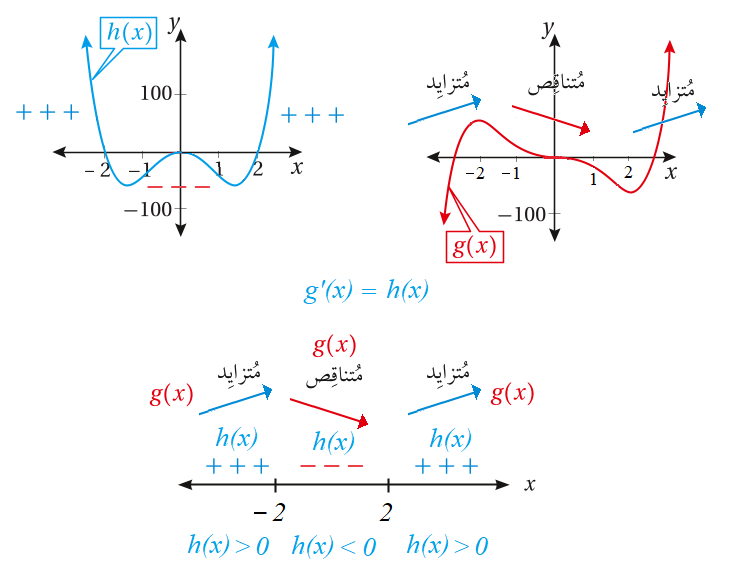
51) 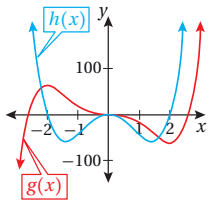 تحدٌ: أستعمل التمثيل البياني المجاور لمنحنيي الاقترانين
تحدٌ: أستعمل التمثيل البياني المجاور لمنحنيي الاقترانين
لتحديد الاقتران الذي يُمثَل مشتقة للآخر ، مُبرّرًا إجابتي.
الحل: