المتتاليات والمتسلسلات الحسابية - حل اسئلة الدرس - الصف الحادي عشر خطة جديدة - رياضيات فصل ثاني - مدرسة جواكاديمي

أتحقق من فهمي

ص: 166

أحدد إذا كانت كل متتالية مما يأتي حسابية أم لا:

$a) 7, 4, 1, - 2, . . .$

الفرق ثابت، حسابية أساسها 3-

$b) 0, 6, 13, 19, . . .$

الفرق غير ثابت، ليست حسابية

أتحقق من فهمي

ص: 168

أجد الحد العام لكل متتالية حسابية مما يأتي، ثم أجد الحد الخامس عشر منها:

$a) 1, - 2, - 5, . . .$

$a_{1} = 1, b = - 3 a_{n} = a_{1} + (n - 1) d 1 + (n - 1) - 3 a_{n} = - 3 n + 4 a_{15} = - 41$

$b) a_{10} = - 11, d = 2$

$a_{n} = a_{1} + (n - 1) d a_{n} = a_{1} + (n - 1) 2 a_{10} = a_{1} + 9 \times 2 = - 11 a_{1} = - 27 a_{n} = - 27 + (n - 1) 2 a_{n} = 2 n - 31 a_{15} = - 1$

أتحقق من فهمي

ص: 169

أجد الحد العام للمتتالية الحسابية التي فيها $a_{7} = 71$ ، و $a_{16} = 26$ .

$26 = a_{1} + 15 d, 71 = a_{1} + 6 d a_{1} = 101, d = - 5 a_{n} = - 5 n + 106$

أتحقق من فهمي

ص: 170

أجد 3 أوساط حسابية بين العددين 55 و 115.

$n = 5, a_{1} = 55, a_{5} = 115 a_{5} = 55 + 4 \times d = 115 d = 15 55, 70, 85, 100, 115$

أتحقق من فهمي

ص: 172

a) أجد مجموع حدود المتسلسلة الحسابية: 159+...+23+15+7.

$159 = 7 + 8 n (n - 1) n = 20 S_{20} = \frac{20}{2} (7 + 159) = 1660$

b) أجد مجموع الحدود السبعة عشر الأولى من المتسلسلة الحسابية: ...+2+5+8.

$d = 5 - 8 = - 3 S_{17} = \frac{17}{2} (2 (8) + 16 \times - 3) = - 272$

أتحقق من فهمي

ص: 173

بيئة: ضمن خطة إحدى المؤسسات الخيرية لزيادة المساحة الخضراء في المدينة، أنفقت المؤسسة 300 JD في السنة الأولى على حملات التوعية، وأخذت تخطط لزيادة إنفاقها السنوي على هذه الحملات بنحو 400 JD سنويا على مدار 10 أعوام:

a) أبين أن أنفاق الجمعية السنوي يمثل متتالية حسابية.

بما أن الزيادة السنوية ثابتة وتساوي 400، فإن إنفاق الجمعية السنوي يشكل متتالية حسابية أساسها 400.

b) أجد الحد العام للمتتالية الحسابية.

$a_{n} = a_{1} + (n - 1) d a_{n} = 300 + (n - 1) 400 a_{n} = 400 n - 100$

c) ما قيمة المبلغ الذي سوف تنفقه المؤسسة في آخر عام من الخطة؟

$a_{10} = 400 \times 10 - 100 a_{10} = 3900$

d) أجد مجموع ما سوف تنفقه المؤسسة في 10 أعوام.

$S_{10} = \frac{10}{2} (300 + 3900) = 21000$

أتدرب وأحل المسائل

أحدد إذا كانت كل متتالية مما يأتي حسابية أم لا:

$1) 10, 11, 14, 15, 18, 19, . . .$

ليست حسابية (الفرق غير ثابت)

$2) 12, 6, 0, - 6, - 12, . . .$

حسابية أساسها 6- (الفرق ثابت)

$3) 3, 5, 9, 15, 23, . . .$

ليست حسابية (الفرق غير ثابت)

أجد الحد العام لكل متتالية حسابية مما يأتي، ثم أجد الحد الثلاثين منها:

$4) 25, 58, 91, 124, . . .$

$a_{1} = 25, d = 33 a_{n} = a_{1} + (n - 1) d a_{n} = 25 + (n - 1) 33 a_{n} = 33 n - 8 a_{30} = 982$

$5) 48.7, 55.1, 61.5, 67.9, . . .$

$a_{1} = 48.7, d = 6.4 a_{n} = a_{1} + (n - 1) d a_{n} = 48.7 + (n - 1) 6.4 a_{n} = 6.4 n + 42.3 a_{30} = 234.3$

$6) 45, 57, 69, 81, . . .$

$a_{1} = 45, d = 12 a_{n} = a_{1} + (n - 1) d a_{n} = 45 + (n - 1) 12 a_{n} = 12 n + 33 a_{30} = 393$

$7) - 1, - \frac{1}{3}, \frac{1}{3}, 1, . . .$

$a_{1} = - 1, d = \frac{2}{3} a_{n} = a_{1} + (n - 1) d a_{n} = - 1 + (n - 1) \frac{2}{3} a_{n} = \frac{2}{3} n - \frac{5}{3} a_{30} = \frac{55}{3}$

$8) a_{5} = 27.6, a_{10} = 24.1$

$a_{n} = a_{1} + (n - 1) d a_{5} = a_{1} + 4 d = 27.6 a_{10} = a_{1} + 9 d = 24.1 = - 5 d = 3.5 d = - 0.7 a_{n} = a_{1} + (n - 1) d a_{10} = a_{1} + 9 \times - 0.7 = 24.1 a_{1} = 30.4 a_{n} = - 0.7 n + 31.1 a_{30} = 10.1$

$9) a_{17} = - 5, d = - \frac{1}{2}$

$a_{n} = a_{1} + (n - 1) d a_{17} = a_{1} + 16 \times - \frac{1}{2} = - 5 a_{1} = 3 a_{n} = 3 + (n - 1) - \frac{1}{2} a_{n} = - \frac{1}{2} n + \frac{7}{2} a_{30} = - \frac{23}{2}$

10) أجد 3 أوساط حسابية بين العددين 9 و 37.

$n = 5, a_{1} = 9, a_{5} = 37 a_{n} = a_{1} + (n - 1) d a_{5} = 9 + 4 \times d = 37 d = 7 9, 16, 23, 30, 37$

11) أجد 4 أوساط حسابية بين العددين 3 و 88.

$n = 6, a_{1} = 3, a_{6} = 88 a_{n} = a_{1} + (n - 1) d a_{6} = 3 + 5 \times d = 88 d = 17 3, 20, 37, 54, 71, 88$

20,37,54,71

12) أجد 5 أوساط حسابية بين العددين 62- و 8-.

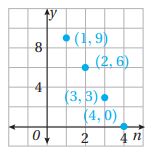
$n = 7, a_{1} = - 62, a_{7} = - 8 a_{n} = a_{1} + (n - 1) d a_{7} = - 62 + 6 \times d = - 8 d = 9 - 62, - 53, - 44, - 35, - 26, - 17, - 8$

13) أكتب قاعدة المتتالية الحسابية التي مثلت بعض حدودها بيانيا في المستوى الإحداثي المجاور.

$9, 6, 3, 0 a_{1} = 9, d = - 3 a_{n} = 9 + (n - 1) - 3 a_{n} = - 3 n + 12$

أجد مجموع المتسلسلات الحسابية الآتية:

$14) 1 + 5 + 9 + . . . + 401$

$401 = 1 + 4 (n - 1) n = 101, S_{101} = \frac{101}{2} (1 + 401) = 20301$

$15) 0.7 + 2.7 + 4.7 + . . . + 56.7$

$56.7 = 0.7 + 2 (n - 1) n = 29, S_{29} = \frac{29}{2} (0.7 + 56.7) = 832.3$

$16) \sum_{n = 1}^{80} (2 n - 2)$

$a_{1} = 0, a_{80} = 158, S_{80} = \frac{80}{2} (0 + 158) = 6320$

أجد المجاميع الجزئية لكل من المتسلسلات الحسابية الآتية:

17) الحدود العشرة الأولى من المتسلسلة: ...+35+30+25+20.

$n = 10, a_{1} = 20, d = 5 S_{10} = \frac{10}{2} (2 (20) + (10 - 1) \times 5) = 425$

18) الحدود الخمسة عشر الأولى من المتسلسلة: ...+16.5+14+11.5+9.

$n = 15, a_{1} = 9, d = 2 s_{15} = \frac{15}{2} (2 (9) + (15 - 1) \times 2.5) = 397.5$

19) الحدود العشرة الأولى من مضاعفات العد 6.

$n = 10, a_{1} = 6, d = 6 S_{10} = \frac{10}{2} (6 + 60) = 330$

20) أول 100 عدد فردي من مجموعة الأعداد الصحيحة الموجبة.

$n = 100, a_{1} = 1, d = 2 S_{100} = \frac{100}{2} (2 (1) + (100 - 1) \times 2) = 10000$

يبين الشكل المجاور نمطا هندسيا يمثل عدد النقاط في نماذجه متتالية:

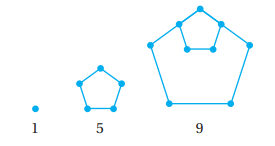
21) أبين أن عدد النقاط في النماذج يمثل متتالية حسابية.

1,5,9

ألاحظ أن الفرق بين كل حدين متتابعين ثابت، وأنه يساوي 4، أي أن المتتالية حسابية أساسها 4.

22) أجد الحد العام للمتتالية الحسابية.

$a_{n} = a_{1} + (n - 1) d a_{n} = 1 + (n - 1) 4 a_{n} = 4 n - 3$

23) هل يوجد نموذج يحوي 397 نقطة؟ أبرر إجابتي.

$397 = 4 n - 3 n = 100$

بما أن n عدد صحيح موجب، إذن يوجد نموذج يحوي 397 نقطة.

متسلسلة حسابية حدها الثالث 51، وحدها الحادي عشر 187:

24) أثبت أن المتسلسلة تمثل مضاعفات العدد 17.

$51 = a_{1} + 2 d 187 = a_{1} + 10 d d = 17, a_{1} = 17 a_{n} = 17 n$

25) أجد مجموع مضاعفات العدد 17 التي تقع بين 0 و 1000.

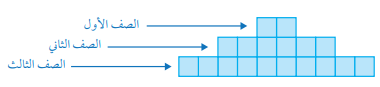
$1000 \div 17 \approx 58.8 S_{58} = \frac{58}{2} (17 + 17 \times 58) = 29087$

26) يبين الشكل المجاور الصفوف الثلاثة الأولى من نمط هندسي مكون من مربعات. أجد عدد المربعات الكلي في 20 صفا.

$2, 6, 10, . . . S_{20} = \frac{20}{2} (2 (2) + (20 - 1) \times 4) = 800$

27) متسلسلة حسابية منتهية، حدها الأول 10، وأساسها 4، ومجموع حدودها 792، ما عدد حدود هذه المتسلسلة؟

$792 = \frac{n}{2} (2 (10) + 9 n - 1 \times 4) n^{2} + 4 n - 396 = 0 (n - 18) (n + 22) = 0 n = 18$

28) إذا كان مجموع أول n حدا من حدود متسلسلة حسابية هو $n^{2} + 4 n$ ، فأجد حدها المئة.

$S_{n} = n^{2} + 4 n S_{1} = 5 a_{1} = 5 S_{2} = 12 a_{2} = 12 - 5 = 7 d = 7 - 5 = 2 a_{n} = 2 n + 3 a_{100} = 203$

أخذت حنين تقرأ صفحات من كتاب يوميا مدة 7 أيام، بدءا بيوم الأحد الذي قرأت فيه 15 صفحة، ثم قرأت في اليوم التالي 21 صفحة، ثم قرأت في اليوم الذي يليه 27 صفحة:

29) أبين ما تقرأه حنين يوميا من صفحات يمثل متتالية حسابية.

$15, 21, 27, . . .$

ألاحظ أن الفرق بين كل حدين متتابعين ثابت، وأنه يساوي 6، أي أن المتتالية حسابية أساسها 6.

30) كم صفحة قرأت حنين يوم الجمعة.

$a_{6} = 55$

31) أجد المجموع الكلي لعدد الصفحات التي قرأتها حنين في الأيام السبعة.

$S_{7} = 231$

متسلسلة حسابية، حدها الأول a، وأساسها d، ومجموع حدودها الثلاثين الأولى يساوي ضعف مجموع حدودها العشرين الأولى.

32) أثبت أن $a = \frac{11 d}{2}$ .

$S_{30} = 2 S_{20} \frac{30}{2} (2 a + 29 d) = 2 \times \frac{20}{2} (2 a + 19 d) a = \frac{11}{2} d$

33) إذا كان مجموع الحدود الثلاثين الأولى هو 400، فأجد قيمتي a و d.

$400 = \frac{30}{2} (2 a + 29 \times \frac{2}{11} a) a = \frac{11}{3}, d = \frac{2}{3}$

مهارات التفكير العليا

34) تبرير: متتالية حسابية، حدها العاشر ضعف حدها الرابع، وحدها الثامن عشر 50، أجد الحد الأول من المتتالية، مبررا إجابتي.

$a_{10} = 2 a_{4} a_{1} + 9 d = 2 (a_{1} + 3 d) a_{1} = 3 d a_{18} = 50 a_{1} = 17 d = 50 3 d + 17 d = 50 d = 2.5 a_{1} = 7.5$

35) تحد: إذا كان مجموع أول n حدا من حدود المتسلسلة هو $6 n^{2} + 8 n$ ، فأثبت أن هذه المتسلسلة حسابية.

$S_{n} = 6 n^{2} + 8 n a_{n} = S_{n} - S_{n - 1} = (6 n^{2} + 8 n) - (6 {(n - 1)}^{2} + 8 (n - 1)) = 12 n + 2$

ألاحظ أن الحد العام للمتتالية هو على صورة الحد العام للمتتالية الحسابية، إذن هذه المتتالية حسابية.

36) تحد: إذا كان $3, a - b, 3 a - 4 b, 2 a + 2 b$ تمثل الحدود الأربعة الأولى من متسلسلة حسابية، حيث a و b ثابتان، فأجد مجموع أول 25 حدا من المتسلسلة.

$3, a - b, 3 a - 4 b, 2 a + 2 b (a - b) - 3 = 3 a - 4 b - (a - b) a - 2 b = - 3 (2 a + 2 b) - (3 a - 4 b) = (3 a - 4 b) - (a - b) 3 a - 9 b = 0 a = 3 b b = - 3, a = - 9 3, - 6, - 15, - 24 a_{1} = 3, d = - 9 S_{25} = \frac{25}{2} (2 (3) - (24) \times - 9) = - 2625$

تبرير: متتالية حسابية فيها الحدان المتتاليان x و y:

37) أجد الحد التالي للحد y بدلالة x و y.

$. . ., x, y, . . . d = y - x a = y + (y - x) = 2 y - x$

38) إذا كان x يمثل الحد الثامن من المتتالية، فأجد الحد الأول بدلالة x و y.

$a_{8} = a_{1} + 7 d = a_{1} + 7 (y - x) x = a_{1} + 7 (y - x) a_{1} = 8 x - 7 y$

حل اسئلة كتاب التمارين

أجد الحد العام لكل متتالية حسابية مما يأتي، ثم أجد الحد العشرين منها:

$1) a_{6} = - 8, a_{15} = - 62$

$a_{n} = - 6 n + 28, a_{20} = - 92$

$2) a_{11} = 43, d = 5$

$a_{n} = 5 n - 12, a_{20} = 88$

$3) 25, 26.5, 28, 29.5, . . .$

$a_{n} = 1.5 n + 23.5, a_{20} = 53.5$

اذا كانت المتتالية الآتية:...,20,27,34,41 حسابية، فأجد:

4) الحد 100 من المتتالية.

$a_{n} = 7 n + 13 a_{100} = 713$

5)أكبر حد أقل من 200.

$a_{26} = 195$

6) مجموع الأعداد العشرة الأولى من المتتالية.

$S_{10} = 515$

أجد مجموع الحدود الثلاثين الأولى لكل مما يأتي:

7)متسلسلة حدها الأول 7، وحدها العام $1 + 6 n$ .

$S_{30} = 2820$

8) متتالية حدها الاول 13، وحدها العام $8 n + 5$ .

$S_{30} = 3870$

مسارح: مسرح في صفه الأول 10 مقاعد، وفي صفه الثاني 12 مقعد، وفي صفه الثالث 14 مقعد، وهكذا حتى الصف الأخير منه:

9) أبين أن عدد المقاعد في صفوف المسرح يشكل متتالية حسابية.

$14 - 12 = 2, 12 - 10 = 2$

متتالية حسابية أساسها 2 (الفرق ثابت)

10) أجد الحد العام للمتتالية الحسابية.

$a_{n} = 2 n + 8$

11) اذا كان في المسرح 14 صفا من القاعد، فكم مقعدا في المسرح؟

$S_{14} = 322$

متسلسلة حسابية مجموع حدودها العشرين الأولى 730، ومجموع حدودها الثلاثين الأولى 1545:

12) أجد الحد الأول من المتسلسلة.

$a_{1} = 8$

13) ما أساس المتسلسلة؟

$d = 3$

14) أجد عدد حدود المتسلسلة التي تقل عن 101.

$31$

رياضيات فصل ثاني

الحادي عشر خطة جديدة

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS