رياضيات فصل ثاني

أتحقق من فهمي

ص: 178

أحدد إذا كانت كل متتالية مما يأتي هندسية أم لا:

$a) 3,12,48,192,...$

$$\begin{gathered} \frac{a_2}{a_1}=\frac{12}{3}=4 \\ \frac{a_3}{a_2}=\frac{48}{12}=4 \\ \frac{a_4}{a_3}=\frac{192}{48}=4 \end{gathered}$$

المتتالية هندسية أساسها 4

$b) -10,10,-10,10,...$

$$\begin{gathered} \frac{a_2}{a_1}=\frac{10}{-10}=-1 \\ \frac{a_3}{a_2}=\frac{-10}{10}=-1 \\ \frac{a_4}{a_3}=\frac{10}{-10}=-1 \end{gathered}$$

المتتالية هندسية أساسها 1-

أتحقق من فهمي

ص: 180

أجد الحد العام لكل متتالية هندسية مما يأتي، ثم أجد الحد العاشر منها:

$a) 5,15,45,...$

$$\begin{gathered} a_1=5 , r=3 \\ {a}_n=a_1{\left(r\right)}^{n-1}{a}_n=5{\left(3\right)}^{n-1} , a_{10}=98415 \end{gathered}$$

$b) a_1=3; r=-2$

$a_n=a_1{\left(r\right)}^{n-1}{a}_n=3{(-2)}^{n-1} , a_{10}=-1536$

أتحقق من فهمي

ص: 181

أجد الحد العام لمتتالية هندسية التي فيها $a_4=3 و،a_2=12$.

$$\begin{gathered} a_4=a_1{\left(r\right)}^3=3.......\left(1\right) \\ {a}_2=a_1\left(r\right)=12 \\ {a}_1=\frac{12}{r}...........\left(2\right) \\ \frac{12}{r}{\left(r\right)}^3=3 \\ {r}^2=\frac{1}{4} \\ r=\pm \frac{1}{2} \\ {a}_1=\pm 24 \\ {a}_n=a_1{\left(r\right)}^{n-1}{a}_n=24{\left(\frac{1}{2}\right)}^{n-1} وأ a_n=-24{(-\frac{1}{2})}^{n-1} \end{gathered}$$

أتحقق من فهمي

ص: 182

أجد 4 أوساط هندسية بين العددين 9 و 288.

$$\begin{gathered} n=6 , a_1=9 , a_6=288 \\ {a}_6=a_1{\left(r\right)}^5=288 \\ =9{\left(r\right)}^5=288 \\ {r}^5=32 \\ r=2 \\ 9,18,36,72,144,288 \end{gathered}$$

أتحقق من فهمي

ص: 183

a) أجد مجموع الحدود السبعة الأولى من المتسلسلة الهندسية: $3-6+12-24+...$.

$$\begin{gathered} a_1=3 , r=-2 , n=7 \\ {S}_7=\frac{3(1-{(-2)}^7)}{1--2} \\ 129 \end{gathered}$$

b) أجد مجموع المتسلسلة الهندسية: $\sum _{k=1}^8 5{\left(2\right)}^{k-1}$.

$$\begin{gathered} n=8 , r=2 , a_1=5 \\ {S}_8=\frac{5(1-2^8)}{1-2} \\ 1275 \end{gathered}$$

أتحقق من فهمي

ص: 186

أجد مجموع المتسلسلات الهندسية اللانهائية الآتية (إن أمكن):

$a) 1+0.1+0.01+...$

$$\begin{gathered} a_1=1 , r=0.1(r<1) \\ {S}_{\infty }=\frac{a_1}{1-r} \\ {S}_{\infty }=\frac{100}{9} \end{gathered}$$

$b) 1-2+4-8+...$

المتسلسلة متباعدة لا يمكن إيجاد مجموع حدودها.

$c) \sum _{n=1}^{\infty } 9{(0.2)}^{n-1}$

$$\begin{gathered} a_1=9 , r=0.2 \\ {S}_{\infty }=\frac{9}{0.8} \\ {S}_{\infty }=\frac{45}{4} \end{gathered}$$

أتحقق من فهمي

ص: 187

أكتب العدد العشري الدوري $0.\overline{57}$ في صورة كسر عادي.

$$\begin{gathered} 0.\overline{57}=0.57+0.0057+0.000057+... \\ {a}_1=0.57 \\ r=\frac{0.0057}{0.57}=0.01 \\ {S}_{\infty }=\frac{a_1}{1-r}=\frac{0.57}{1-0.01}=\frac{0.57}{0.99}=\frac{57}{99}=\frac{19}{33} \end{gathered}$$

أتحقق من فهمي

ص: 188

كرة: أسقطت كرة سلة من ارتفاع 20m رأسيا في اتجاه أرض أفقية وقد ارتدت كل مرة مسافة تعادل ما نسبته $70\raisebox{1ex}{$ 0$}\!\left/ \!\raisebox{-1ex}{$0$}\right.$ من المسافة السابقة. بافتراض أن الكرة سقطت رأسيا ثم ارتدت رأسيا عددا لا نهائيا من المرات، أجد المسافة التي قطعتها الكرة حتى توقفت.

$$\begin{gathered} 20+2(14+9.8+6.86+...) \\ 20+2\left(\frac{14}{1-0.7}\right) \\ =113.33 m \end{gathered}$$

أتدرب وأحل المسائل

أحدد إذا كانت كل متتالية مما يأتي هندسية أم لا:

$1) 96,48,24,12,6,...$

المتتالية هندسية أساسها $\frac{1}{2}$( النسبة ثابتة بين كل حد والحد الذي يسبقه)

$2) \frac{1}{2},\frac{1}{6},\frac{1}{18},\frac{1}{54},\frac{1}{162},...$

المتتالية هندسية أساسها $\frac{1}{3}$( النسبة ثابتة بين كل حد والحد الذي يسبقه)

$3) 0.3,-1.5,7.5,-37.5,187.5,...$

المتتالية هندسية أساسها 5- ( النسبة ثابتة بين كل حد والحد الذي يسبقه)

أجد الحد العام لكل متتالية هندسية مما يأتي، ثم أجد الحد الثامن منها:

$4) 0.04,0.2,1,...$

$$\begin{gathered} a_1=0.04 , r=5 \\ {a}_n=a_1{\left(r\right)}^{n-1}{a}_n=0.04{\left(5\right)}^{n-1} , a_8=3125 \end{gathered}$$

$5) 20,24,28.8$

$$\begin{gathered} a_1=20 , r=\frac{6}{5} \\ {a}_n=20{\left(\frac{6}{5}\right)}^{n-1} , a_8\approx 71.7 \end{gathered}$$

$6) 0.005,0.01,0.02,...$

$$\begin{gathered} a_1=0.005 , r=2 \\ {a}_n=0.005{\left(2\right)}^{n-1} , a_8=0.64 \end{gathered}$$

$7) 3,-6,12,-24,...$

$$\begin{gathered} a_1=3 , r=-2 \\ {a}_n=3{(-2)}^{n-1} , a_8=-384 \end{gathered}$$

$8) e^2,e^4,e^6,e^8,...$

$$\begin{gathered} a_1=e^2 , r=e^2 \\ {a}_n=e^2{\left(e^2\right)}^{n-1} , a_8=e^{16} \end{gathered}$$

$9) 1,\sqrt{2},2,2\sqrt{2},...$

$$\begin{gathered} a_1=1 , r=\sqrt{2} \\ {a}_n={\left(\sqrt{2}\right)}^{n-1} , a_8=8\sqrt{2} \end{gathered}$$

أجد الحد العام لكل من المتتاليات الهندسية الآتية التي أعطي حدان من حدودها:

$10) a_2=12 , a_5=-768$

$$\begin{gathered} a_2=a_{1}r=12 \\ {a}_1=\frac{12}{r}.....\left(1\right) \\ {a}_5=a_1{r}^4=-768.......\left(2\right) \\ {r}^3=-64 \\ r=-4 \\ {a}_1=\frac{12}{-4}=-3 \\ {a}_n=-3{(-4)}^{n-1} \end{gathered}$$

$11) a_2=7 , a_4=1575$

$$\begin{gathered} a_2=a_{1}r=7 \\ {a}_1=\frac{7}{r}.....\left(1\right) \\ {a}_4=a_1{r}^3=1575 \\ {r}^2=225 \\ r=\pm 15 \\ {a}_1=\pm \frac{7}{15} \\ {a}_n=\frac{7}{15}{\left(15\right)}^{n-1} , \\ {a}_n=-\frac{7}{15}{(-15)}^{n-1} \end{gathered}$$

$12) a_3=\frac{1}{3} , a_6=\frac{1}{81}$

$$\begin{gathered} a_3=a_1{r}^2=\frac{1}{3} \\ {a}_1=\frac{1}{3r^2} \\ {a}_6=a_1{r}^5=\frac{1}{81} \\ =\frac{1}{3r^2}{r}^5=\frac{1}{81} \\ {r}^3=\frac{1}{27} \\ r=\frac{1}{3} \\ {a}_1=3 \\ {a}_n=3{\left(\frac{1}{3}\right)}^{n-1} \end{gathered}$$

13) أجد 3 أوساط هندسية بين العددين 7 و 189

$$\begin{gathered} n=5 , a_1=7 , a_5=189 \\ {a}_5=7r^4=189 \\ {r}^4=27 \\ r=\sqrt[4]{27} \\ 7\sqrt[4]{27} , 21\sqrt{3} , 63\sqrt[4]{3} \\ -7\sqrt[4]{27} , 21\sqrt{3} , -63\sqrt[4]{3} \end{gathered}$$

14) أجد 4 أوساط هندسية بين العددين 32 و 1

$$\begin{gathered} n=6 , a_1=72 , a_6=1 \\ {a}_6=32 r^5=1 \\ {r}^5=\frac{1}{32} \\ r=\frac{1}{2} \\ 16,8,4,2 \end{gathered}$$

15) أجد مجموع الحدود الاثني عشر الأولى من المتسلسلة الهندسية: $4-8+16-32+...$

$$\begin{gathered} a_1=4 , r=-2 , n=12 \\ {S}_{12}=\frac{4(1-{(-2)}^{12})}{1--2} \\ {S}_{12}=-5460 \end{gathered}$$

16) أجد مجموع الحدود العشرين الأولى من المتسلسلة الهندسية: $20+22+24.2+26.62+...$

$$\begin{gathered} a_1=20 , r=1.1 , n=20 \\ {S}_{20}=\frac{20(1-{(1.1)}^{20})}{1-1.1} \\ {S}_{20}=1145.49999 \end{gathered}$$

أجد مجموع المتسلسلات الهندسية الآتية:

$17) \sum _{k=1}^5 {\left(\frac{2}{3}\right)}^k$

$$\begin{gathered} a_1=\frac{2}{3} , r=\frac{2}{3} , n=5 \\ {S}_5=\frac{{\displaystyle \frac{2}{3}}(1-{\left({\displaystyle \frac{2}{3}}\right)}^5)}{1-{\displaystyle \frac{2}{3}}} \\ \frac{422}{243} \end{gathered}$$

$18) \sum _{k=0}^{10} 3{\left(\frac{1}{2}\right)}^k$

$$\begin{gathered} a_1=3 , r=\frac{1}{2} , n=10. \\ {S}_{10}=\frac{3(1-{\left({\displaystyle \frac{1}{2}}\right)}^{10})}{1-{\displaystyle \frac{1}{2}}} \\ .\frac{6141}{1024} \end{gathered}$$

$19) 1+3+9+...+2187$

$$\begin{gathered} a_1=1 ,r=3 \\ {a}_n=1{\left(3\right)}^{n-1}=2187 \\ {3}^{n-1}=3^7 \\ n=8 \\ {S}_8=\frac{1(1-3^8)}{1-3} \\ 3280 \end{gathered}$$

أجد مجموع المتسلسلات الهندسية الانهائية الآتية (إن أمكن):

$20) 2+\frac{2}{3}+\frac{2}{9}+\frac{2}{27}+...$

$$\begin{gathered} S_{\infty }=\frac{a_1}{r-1} \\ =\frac{2}{1-{\displaystyle \frac{1}{3}}} \\ {S}_{\infty }=3 \end{gathered}$$

$21) 6-4+\frac{8}{3}-\frac{16}{9}+...$

$$\begin{gathered} a_1=6 \\ r=\frac{-4}{6}=\frac{-2}{3} \\ {S}_{\infty }=\frac{6}{1-{\displaystyle \frac{-2}{3}}}=\frac{6}{{\displaystyle \frac{3}{5}}} \\ {S}_{\infty }=\frac{18}{5} \end{gathered}$$

$22) \sum _{k=1}^{\infty } \frac{1}{2}(3^{k-1})$

المتسلسلة متباعدة لا يمكن إيجاد مجموع حدودها.

أكتب كلا من الأعداد العشرية الدورية الآتية في صورة كسر عادي بأبسط صورة:

$23) 0.\overline{25}$

$$\begin{gathered} 0.\overline{25}=0.25+0.0025+0.000025+... \\ {a}_1=0.25 , r=0.01 \\ {S}_{\infty }=\frac{0.25}{1-0.01}=\frac{0.25}{0.99} \\ \frac{25}{99} \end{gathered}$$

$24) 0.\overline{625}$

$$\begin{gathered} 0.625=0.625+0.000625+0.000000625+... \\ {a}_1=0.625 , r=0.001 \\ {S}_{\infty }=\frac{0.625}{1-0.001}=\frac{0.625}{0.999} \\ \frac{625}{999} \end{gathered}$$

$25) 32.\overline{32}$

$$\begin{gathered} 32+0.\overline{32} \\ 0.\overline{32}=0.32+0.0032+0.000032+... \\ {a}_1=0.32 , r=0.01 \\ {S}_{\infty }=\frac{0.32}{1-0.01} \\ 32+\frac{32}{99}=\frac{3200}{99} \end{gathered}$$

طاقة متجددة: يزداد عدد المنازل التي تعتمد على الطاقة الشمسية في توليد الكهرباء بإحدى المدن عاما تلو الآخر كما في الجدول الآتي:

العام	1	2	3	4	5
عدد المنازل	7000	9800	13720

26) أجد الحد العام لمتتالية  التي تمثل عدد المنازل.

$$\begin{gathered} a_1=7000 , r=\frac{9800}{7000}=\frac{7}{5} \\ {a}_n=a_1{\left(r\right)}^{n-1}{a}_n=7000{\left(\frac{7}{5}\right)}^{n-1} \end{gathered}$$

27) أجد عدد المنازل التي تعتمد على الطاقة الشمسية في توليد الكهرباء  في العام الرابع والعام الخامس.

$$\begin{gathered} a_4=19208 \\ {a}_5=26891 \end{gathered}$$

ادخرت مريم مبلغا من المال في أحد البنوك، وقد بلغ مجموع ما ادخرته في السنة الأولى 2000 JD، ثم ادخرت في كل سنة لاحقة ما نسبته $25 \raisebox{1ex}{$0$}\!\left/ \!\raisebox{-1ex}{$0$}\right.$ أكثر من المبلغ الذي ادخرته في السنة السابقة:

28) ما المبلغ  الذي ستدخره مريم في السنة الثالثة؟

$a_3=2000{\left(\frac{5}{4}\right)}^2=3125$

29) بعد كم سنة سيكون مجموع مدخرات مريم أكثر من 50000 JD؟

$$\begin{gathered} 2000{\left(\frac{5}{4}\right)}^{n-1} >50000 \\ {(1.25)}^{n-1} >25n>1+lo{g}_{1.25}25\approx 15.4 \end{gathered}$$

أي بعد 16 سنة

ندفة الثلج: يمثل النمط الجاور عدد أضلاع ندفة ثلج في مراحلها المتتالية:

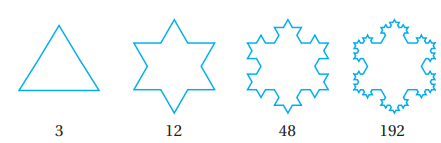
30) أكتب الحد العام لهذه المتتالية.

$$\begin{gathered} a_1=3 , r=4 \\ {a}_n=a_1{\left(r\right)}^{n-1}{a}_n=3{\left(4\right)}^{n-1} \end{gathered}$$

31) أجد عدد أضلاع ندفة الثلج في المرحلة السابعة.

$a_7=3{\left(4\right)}^6=12288$

32) متسلسلة هندسية لانهائية متقاربة، حدها الأول 80، ومجموعها 200، أجد عدد الحدود الأولى التي يلزم جمعها معا ليكون المجموع أكثر من 199

$$\begin{gathered} 200=\frac{80}{1-r} \\ r=\frac{3}{5} \\ \frac{80(1-{\left({\displaystyle \frac{3}{5}}\right)}^n)}{1-{\displaystyle \frac{3}{5}}} >199 \\ n>10.4 \end{gathered}$$

أي أن عدد الحدود المطلوبة هو 11

تمثل $6p+2, 4p+4 , 3p+3$  الحدود الثلاثة الأولى من متتالية هندسية، حيث $p\ne 0$:

33) أجد قيمة الثابت p.

$$\begin{gathered} \frac{4p+4}{6p+2}=\frac{3p+3}{4p+4} \\ \frac{4(p+1)}{2(3p+1)} \\ \frac{(p+1)}{(3p+1)}=\frac{3}{8} \\ 8p+8=9p+3 \\ p=5 \end{gathered}$$

34) أثبت أن المتسلسلة اللانهائية المعطى أول ثلاثة حدود منها متقاربة، ثم أجد مجموعها.

$$\begin{gathered} a_1=6\times 5+2=32 \\ {a}_2=4\times 5+4=24 \\ {a}_3=3\times 5+3=18 \\ 32,24,18 \\ r=\frac{3}{4} \end{gathered}$$

إذن المتتالية هندسية لا منتهية متقاربة

$S_{\infty }=128$

متتالية هندسية أساسها موجب، ومجموع حدودها الأربعة الأولى 105، ومجموع حدودها الثمانية الأولى 1785:

35) أجد الحد الأول من هذه المتتالية، وأساسها

$r=2 , a_1=7$

36) ما عدد حدود المتتالية التي تقل عن 1000؟

$n=8$

مهارات التفكير العليا

37) تحد: أجد الصيغة العامة لمجموع أول n حدا من حدود المتسلسلة: $1\frac{1}{2}+2\frac{1}{4}+3\frac{1}{8}+4\frac{1}{16}+...$

$\sum _{k=1}^{\infty } \frac{1+k{\left(2\right)}^k}{2^k}$

38) مسألة مفتوحة: أجد متتالية هندسية لانهائية متقاربة، مجموعها 1.5

$1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+...$

تبرير: يبين الشكل المجاور نمطا حلزونيا مكونا من قطع  مستقيمة في المستوى الإحداثي. إذا علمت أن القطعة المستقيمة الأولى $\overline{OA}$ طولها 20cm، وأن القطعة المستقيمة الثانية $\overline{AB}$ طولها 10cm، وهي موازية للمحور y، وأن القطعة المستقيمة الثالثة $\overline{BC}$ طولها 5cm، وهي موازية للمحور x، وأن هذا النمط استمر إلى ما لا نهاية، فأجد:

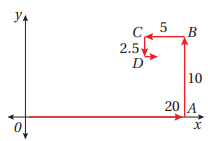
39) مجموع أطوال القطع المستقيمة المكونة للنمط.

$20+10+5+...=\frac{20}{1-0.5}=40$

40) إحداثيي نقطة نهاية النمط الحلزوني.

الإحداثيات x هي: ...-1.25+5-20

وهي تشكل متتالية هندسية حدها الأول 20 وأساسها 0.25-، فيكون مجموعها هو

$S_{\infty }=\frac{20}{1+0.25}=16$

الإحداثيات y هي: ...-0.625+2.5-10

وهي تشكل متتالية هندسية حدها الأول 10 وأساسها 0.25-، فيكون مجموعها هو

$S_{\infty }=\frac{10}{1+0.25}=8$

نقطة نهاية النمط الحلزوني (16,8).

تبرير: يبين الشكل المجاور نمطا هندسيا يمثل عدد المثلثات في نماذجه متتالية:

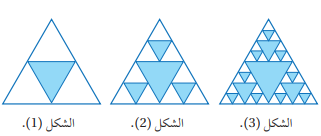
41) املأ الفراغ في الجدول المجاور اعتمادا على النمط.

رقم الشكل	1	2	3	4
عدد المثلثات البيضاء	3	9	27	81
عدد المثلثات الزرقاء	1	4	13	40

42) أكتب الحد العام لمتتالية عدد المثلثات البيضاء في كل شكل.

$a_n=3^n$

43) أكتب الحد العام لمتتالية عدد المثلثات الزرقاء

$a_n=\frac{1}{2}(3^n-1)$

حل أسئلة كتاب التمارين

أحدد إذا كانت كل متتالية مما يأتي هندسية أم لا:

$1) 729,243,81,27,9,....$

هندسة أساسها $\frac{1}{3}$

$2) -0.8,302,-12.8,51.2,-204.8,....$

هندسية أساسها 4-

أجد مجموع المتسلسلات الهندسية الانهائية الآتية:

$3) 1+\frac{3}{4}+\frac{9}{16}+\frac{27}{64}+...$

$S_{\infty }=4$

$4) 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...$

$S_{\infty }=2$

$5) \sum _{k=1}^{\infty } 4{\left(-\frac{1}{2}\right)}^{k-1}$

$S_{\infty }=\frac{8}{3}$

متتالية هندسية حدها الثالث $\frac{8}{3}$، وحدها الخامس $\frac{32}{27}$:

6) أجد الحد الأول من المتتالية.

$a_1=6$

7) ما المجموع اللانهائي لحدود المتتالية؟

$$\begin{gathered} r=\frac{2}{3} \\ {S}_{\infty }=18 \\ r=-\frac{2}{3} \\ {S}_{\infty }=\frac{18}{5} \end{gathered}$$

8) متتالية هندسية لانهائية متقاربة، حدها الأول a، ومجموعها ka، حيث $k>1$. أجد حدها الثاني بدلالة الثابتين a و k.

$a_2=a \left(\frac{k-1}{k}\right)$

9) إذا  كان الحد الأول لمتسلسلة هندسية لانهائية متقاربة x، وأساسها 3x ومجموعها 8، فما قيمة x.

$x=\frac{8}{25}$

10) حواسيب: اشترت رغد حاسوبا، واتفقت مع البائع على أن تدفع من ثمنه 100 JD في الشهر الأول، ثم تدفع في بقية الشهور ما نسبته $80 \raisebox{1ex}{$0$}\!\left/ \!\raisebox{-1ex}{$0$}\right.$ من قيمة دفعة الشهر السابق، مدة عام كامل. كم دينارا سعر الحاسوب؟

$S_{12}\approx 465.64$

بدأ ماهر العمل في إحدى الشركات، وبلغ راتبه الشهري في السنة الأولى 500 JD؛ على أن يزداد الراتب بنسبة $3\raisebox{1ex}{$0$}\!\left/ \!\raisebox{-1ex}{$0$}\right.$ سنويا بعد العام الأول:

11) أكتب قاعدة يمكن استعمالها لتحديد راتب ماهر بعد (n) من السنوات.

$a_n=500{(1.03)}^{n-1}$

12) كم دينارا سيبلغ راتبه الشهري في العام الخامس؟

$a_5=562.754$

13) إذا استمر ماهر في العمل بهذه الشركة 10 سنوات فما مجموع رواتبه في هذه السنوات؟

$S_{120}\approx 561849.786$