رياضيات أدبي فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة اتحقق من فهمي 

أتحقق من فهمي صفحة  62

أكتب كل متسلسلة ممّا يأتي باستعمال رمز المجموع :

a)  3 + 6 + 9 + … + 27

b)  3 + 5 + 7 + 9 + ... 

الحل : 

الحد الأول يساوي  ( 1) 3 ،   الحد الثاني يساوي ( 2) 3،   الحد الثالث يساوي  ( 3) 3 ، والحد الأخير  يساوي ( 9) 3  ،  إذن ، الحد العام :  $a_k = 3k$   ، عدد الحدود  = 9	$\underset{ k=1}{\overset{ 9}{\mathit{a}\mathbf{)} \sum }}\left(3k\right)$
الحد الأول يساوي  1 +( 1) 2 ،   الحد الثاني يساوي 1+( 2) 2 ،   الحد الثالث يساوي 1+ ( 3) 2 ، إذن الحد العام : $a_k = (2k + 1)$   وهي متسلسلة غير منتهية .	$\mathit{b}\mathbf{)}\mathbf{ }\sum _{k=1}^{\infty }(2k +1)$

 

---

أتحقق من فهمي صفحة  62

أجد مجموع المتسلسلة :  $\sum _{k=1}^{ 11}(5k - 3)$

الحل : 

تعويض القيم : $k = 1 , 2 , 3 , 4 , 5 . 6 , 7 . 8 , 9 , 10 , 11$ في الحد العام للمتسلسلة وهو  5k - 3

نحصل على حدود المتسلسلة  ، وهي : $2+7+12+17+22+27+32+37+42+47+52$

إذن مجموع المتسلسة  هو :

                                                     $$\begin{gathered} \underset{ }{\overset{ }{ \sum _{k=1}^{11}(5k-3) = }}2+7+12+17+22+27+32+37+42+47+52 \\ = 297 \end{gathered}$$      $$

---

 

أتحقق من فهمي صفحة  64

مكتبات : رُتِّبت الطاولات في مكتبة المدرسة بحيث تحيط بها الكراسي كما في الشكل الآتي : 

                                                                                                 

أكتب باستعمال رمز المجموع متسلسلة يُمثِّل مجموعها عدد الكراسي في المكتبة، ثم أجد مجموع المتسلسلة.

الحل : 

المتسلسلة  :  14 + 10 + 6 

الحد العام  : $a_k = 4k + 2$

عدد الحدود = 3

المتسلسلة باستخدام رمز المجموع :  $\sum _{k=1}^3(4k+2)$

مجموع المتسلسلة :   $\sum _{k=1}^3(4k+2)= 6 + 10 + 14 = 30$                                       

 

---

أسئلة أتدرب وأحل المسائل

أكتب كُلًا من المتسلسلات الآتية باستعمال رمز المجموع :

$\mathbf{1}\mathbf{)} 1 + 6 + 11 + 16$	$\mathbf{2}\mathbf{)}\mathbf{ }1 + 2 + 3 +... + 50$
$\mathbf{3}\mathbf{)}\mathbf{ }\mathbf{ }2 + 5 + 10 + 17 + 26$	$\mathbf{4}\mathbf{)}\mathbf{ }\frac{1}{2} + \frac{2}{3} + \frac{3}{4} + \frac{4}{5}$
$\mathbf{5}\mathbf{)}\mathbf{ }25 + 50 + 75 + ... + 200$	$\mathbf{6}\mathbf{)}\mathbf{ }5 + 5 + 5 + 5 + 5 + 5$

 

الحل : 

عدد الحدود 4 ، الحد العام : $a_k = 5k - 4$	$$\begin{gathered} \mathbf{1}\mathbf{)} 1 + 6 + 11 + 16 \\ \sum _{k=1}^4(5k-4) \end{gathered}$$
عدد الحدود 50 ، الحد العام : $a_k = k$	$$\begin{gathered} \mathbf{2}\mathbf{)}\mathbf{ }1 + 2 + 3 +... + 50 \\ \sum _{k=1}^{50} k \end{gathered}$$
عدد الحدود 5 ، الحد العام :$a_k = k^2 +1$	$$\begin{gathered} \mathbf{3}\mathbf{)}\mathbf{ }\mathbf{ }2 + 5 + 10 + 17 + 26 \\ \sum _{k=1}^5(k^2+1) \end{gathered}$$
عدد الحدود 4 ، الحد العام :$a_k = \left(\frac{k}{k+1}\right)$	$$\begin{gathered} \mathbf{4}\mathbf{)}\mathbf{ }\frac{1}{2} + \frac{2}{3} + \frac{3}{4} + \frac{4}{5} \\ \sum _{k=1}^4(\frac{k}{k+1}) \end{gathered}$$
الحد الاول  (1)25  ، الحد الثاني (2)25  ... الحد الأخير  (8)25 إذن عدد الحدود 8 ، الحد العام : $a_k = 25k$	$$\begin{gathered} \mathbf{5}\mathbf{)}\mathbf{ }25 + 50 + 75 + ... + 200 \\ \sum _{k=1}^8(25k) \end{gathered}$$
عدد الحدود 6 ، الحد العام : $a_k = 5$	$$\begin{gathered} \mathbf{6}\mathbf{)}\mathbf{ }5 + 5 + 5 + 5 + 5 + 5 \\ \sum _{k=1}^{6}5 \end{gathered}$$

 

---

أجد مجموع كلٍّا من المتسلسلات الآتية :

$\mathbf{7}\mathbf{)}\mathbf{ }\sum _{k=1}^5(k + 2)$	$\mathbf{8}\mathbf{)}\mathbf{ }\underset{k=1 }{\overset{10 }{\sum (k^2}}-1)$
$\mathbf{9}\mathbf{)}\mathbf{ }\sum _{k=1}^{40}-5$	$\mathbf{10}\mathbf{)}\mathbf{ }\sum _{k=1}^{5}k$
$\mathbf{11}\mathbf{)}\mathbf{ }\underset{k=1}{\overset{4}{\sum (}}3k + 1)$	$\mathbf{12}\mathbf{)}\mathbf{ }\sum _{k=1}^{55}9$

 

الحل : 

 

بتعويض القيم : $k = 1 , 2 , 3 , 4 , 5$   في الحد العام  : $a_k= k+2$	$7) \sum _{k=1}^5(k + 2) = 3 + 4 + 5 + 6 + 7 = 25$
بتعويض القيم  : $k = 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10$  في الحد العام : $a_k = k^2-1$	$\mathbf{8}\mathbf{)}\mathbf{ } \sum _{k=1}^{10} (k^2-1) =0 +3 +8 +15 +24 + 35 + 48 + 63 +80 +99 = 375$
مجموع الحد الثابت ( c) إلى نفسه ( n) من المرّات. $\sum _{k=1}^n c = n \times c$	$\mathbf{9}\mathbf{)}\mathbf{ }\sum _{k=1}^{40}-5 = 40 \times -5 = - 200$
مجموع الأعداد الصحيحة المتتالية من (1) إلى (n) .   $\underset{k=1}{\overset{n}{\sum }}K = \frac{n(n+1)}{2}$	$\mathbf{10}\mathbf{)}\mathbf{ }\sum _{k=1}^{5}k =\frac{5(5+1)}{2} =15$
بتعويض القيم  : $k = 1 , 2 , 3 , 4$ في الحد العام : $a_k = 3k + 1$	$\mathbf{11}\mathbf{)}\mathbf{ }\underset{k=1}{\overset{4}{\sum (}}3k + 1) = 4 + 7 + 10 +13 = 34$
.
مجموع الحد الثابت ( c) إلى نفسه ( n) من المرّات. $\sum _{k=1}^n c = n \times c$	$\mathbf{12}\mathbf{)}\mathbf{ }\sum _{k=1}^{55}9 = 55 \times 9 = 495$

 

---

13) بناء : بنى عامل جدارًا يحوي 20 صفًّا من الطوب، وقد أراد إضفاء لمسة جمالية عليه ، فوضع 80 طوبة مُلوَّنة في  الصف الأول (السفلي) ، ثم وضع في كل صف يعلوه عددًا من الطوب المُلوَّن يقل بمقدار طوبتين عن عدد الطوب المُلوَّن في الصف السابق له. أستعمل رمز المجموع لكتابة متسلسلة تُمثِّل مجموع الطوب المُلوَّن الذي استعمله  العامل في بناء الجدار ، ثم أجد مجموع المتسلسلة.

الحل : 

المتسلسلة  : $80 + 78 + 76 + 74 +...+ 42$

عدد الحدود  = 20 

المتسلسلة باستخدام رمز المجموع :  $\sum _{k=1}^{20}( 82 - 2k)$                     

مجموع المتسلسة :   

باستخدام صيغة جمع الثابت إلى نفسه من 1 إلى n من المرات  ، وصيغة جمع الاعداد الصحيحة المتتالية من 1 إلى n  من المرات.

$\sum _{k=1}^{20}( 82 - 2k) = (20 \times 82) - 2\left(\frac{20(20+1)}{2}\right) = 1220$

 

 

 

 

---

14) هندسة : أستعمل رمز المجموع لكتابة متسلسلة تُمثِّل مجموع المربعات في الشكل الآتي عندما يصبح عدد الصفوف فيه (n).  

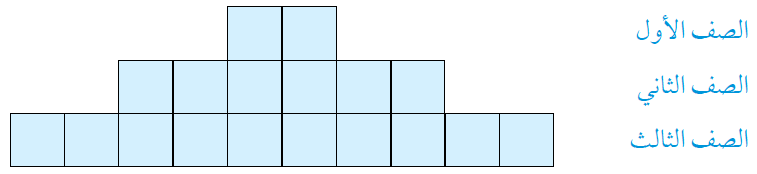
الحل : 

المتسلسلة  : $2 + 6 + 10 +...$

عدد الحدود  =  n 

المتسلسلة باستخدام رمز المجموع : $\sum _{k=1}^n(4k - 2)$

 

---

15) أحُلّ المسألة الواردة في بند (مسألة اليوم).

مسألة اليوم : يمارس هيثم تمارين الضغط بانتظام،وقد استطاع أداء 25 ضغطة في الأسبوع الأول ، ثم تمكَّن من زيادة عددها أسبوعيًّا بمقدار 10 ضغطات.ما عدد الضغطات التي يُمكِنه أداؤها بعد 16 أسبوعًا؟

 

 

 

 

 

الحل : 

المتسلسلة  : $25 + 35 +45 +... +175$

عدد الحدود  =  16

المتسلسلة باستخدام رمز المجموع : $\sum _{k=1}^{16}(10k + 15)$

مجموع المتسلسة :   

باستخدام صيغة جمع الثابت إلى نفسه من 1 إلى n من المرات  ، وصيغة جمع الاعداد الصحيحة المتتالية من 1 إلى n  من المرات.

$\sum _{k=1}^{16}( 10k +15) = 10 \left(\frac{16(16+1)}{2}\right) + (16 \times 15) =1600$

 

 

 

---

أسئلة مهارات التفكير العليا 

16) أكتشف الخطأ : أوجدت ولاء مجموع المتسلسلة :   $\sum _{ k=1}^5(2k + 7)$ على النحو الآتي : 

 

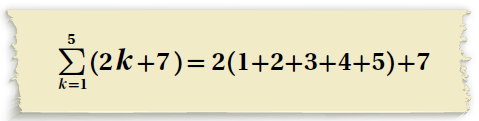
أكتشف الخطأ في حلّ ولاء ، ثم أُصحِّحه.

الحل : 

أخطأت ولاء في عملية التعويض في الحد العام  ، والصحيح  : 

$$\begin{gathered} \sum _{k=1}^5(2k+7) = 2\left(1\right) + 7 + 2\left(2\right)+ 7 + 2\left(3\right) + 7 + 2\left(4\right) +7 + 2\left(5\right) + 7 \\ \sum _{k=1}^5(2k+7) = 9 +11 +13 +15 + 17 = 65 \end{gathered}$$

 

17) أكتشف المختلف : أيُّ الآتية مختلف عن الثلاثة الأُخرى ، مُبررًا إجابتي؟

الحل : 

المختلف  :  $\sum _{k=1}^5{i}^2$ مجموعها = 55 ، بينما الثلاث الأخرى قيمة كل منها  = 91 

 

---

18) تحدّ : اثبت انّ : $\sum _{k=1}^{n}c = n \times c$ ، حيث c عدد حقيقي. 

الحل : 
 

(n مرة)	$\sum _{k=1}^{n}c =c + c +c +...+c$
إخراج c عامل مشترك	$\sum _{k=1}^{n}c =c ( 1 +1 +1 +1...+1)$
	$\sum _{k=1}^{n}c =c (n\times 1) \Rightarrow \sum _{k=1}^{n}c = n\times c$

 

 

 

 

 

 

 

---

 

أسئلة كتاب التمارين 

أكتب كل متسلسلة ممّا يأتي باستعمال رمز المجموع، ثم أُصنِّفها إلى منتهية وغير منتهية :

$\mathbf{1}\mathbf{)}\mathbf{ }5 + 11 + 17 + 23 + ...$	$\mathbf{2}\mathbf{)}\mathbf{ }- 10 - 4 + 2 + 8$
$\mathbf{3}\mathbf{)}\mathbf{ }5 + 23 + 53 + 95 + 149$	$\mathbf{4}\mathbf{)}\mathbf{ }7 + 7 + 7 + 7 +...$
$\mathbf{5}\mathbf{)}\mathbf{ }- 1 - 5 - 9 - 13 - ...$	$\mathbf{6}\mathbf{)}\mathbf{ }- 9 - 9 - 9 - 9 - 9 - 9$

الحل : 

متسلسلة غير منهية .	$$\begin{gathered} \mathbf{1}\mathbf{)}\mathbf{ }5 + 11 + 17 + 23 + ... \\ \sum _{k=1}^{\infty }(6k-1) \end{gathered}$$
متسلسلة منهية .	$$\begin{gathered} \mathbf{2}\mathbf{)}\mathbf{ }- 10 - 4 + 2 + 8 \\ \sum _{k=1}^4(6k-16) \end{gathered}$$
متسلسلة منهية .	$$\begin{gathered} \mathbf{3}\mathbf{)}\mathbf{ }5 + 23 + 53 + 95 + 149 \\ \sum _{k=1}^5(6k^2 -1) \end{gathered}$$
متسلسلة غير منهية .	$$\begin{gathered} \mathbf{4}\mathbf{)}\mathbf{ }7 + 7 + 7 + 7 +... \\ \sum _{k=1}^{\infty }7 \end{gathered}$$
متسلسلة غير منهية .	$$\begin{gathered} \mathbf{5}\mathbf{)}\mathbf{ }- 1 - 5 - 9 - 13 - ... \\ \sum _{k=1}^{\infty }(3-4k) \end{gathered}$$
متسلسلة منهية .	$$\begin{gathered} \mathbf{6}\mathbf{)}\mathbf{ }- 9 - 9 - 9 - 9 - 9 - 9 \\ \sum _{k=1}^6(-9) \end{gathered}$$

 

---

أجد مجموع كلٍّ من المتسلسلات الآتية :

$\mathbf{7}\mathbf{)}\mathbf{ }\sum _{k=1}^6(7k -5)$	$\mathbf{8}\mathbf{)}\mathbf{ }\sum _{k=1}^5(2k^3-4)$
$\mathbf{9}\mathbf{)}\mathbf{ }\sum _{k=1}^4(9 - k^2 )$	$\mathbf{10}\mathbf{)}\mathbf{ }\underset{k=1 }{\overset{6 }{\sum \mathbf{ }4k}}$
$\mathbf{11}\mathbf{)}\mathbf{ }\underset{\mathrm{k}=1 }{\overset{3 }{\sum \mathbf{ }(3\mathrm{k} - 3)}}$	$\mathbf{12}\mathbf{)}\mathbf{ }\sum _{k=1}^9(-2)$

الحل : 

بتعويض قيم $k = 1 , 2 , 3 , 4 ,5 , 6$ في الحد العام	$\mathbf{7}\mathbf{)}\mathbf{ }\sum _{k=1}^6(7k -5) =2 +9 +16 +23 +30 +37 = 119$
بتعويض قيم $k = 1 , 2 , 3 , 4 ,5$ في الحد العام	$\mathbf{8}\mathbf{)}\mathbf{ }\sum _{k=1}^5(2k^3-4) =-2 + 12 +50+124 + 246 = 430$
بتعويض قيم $k = 1 , 2 , 3 , 4$ في الحد العام	$\mathbf{9}\mathbf{)}\mathbf{ }\sum _{k=1}^4(9 - k^2 ) = 8 +5 +0 +(-7) = 6$
بتعويض قيم  $k = 1 , 2 , 3 , 4 ,5 , 6$ في الحد العام	$\mathbf{10}\mathbf{)}\mathbf{ }\underset{k=1 }{\overset{6 }{\sum \mathbf{ }4k}}\mathbf{ }= 4 +8 +12 +16 +20 +24 = 84$
بتعويض قيم  $k = 1 , 2 , 3$  في الحد العام	$\mathbf{11}\mathbf{)}\mathbf{ }\underset{\mathrm{k}=1 }{\overset{ 3 }{\sum (3\mathrm{k} - 3)}}= 0 + 3 + 6 = 9$
باستخدام صيغة جمع الثابت إلى نفسه من 1 إلى n من المرات	$\mathbf{12}\mathbf{)}\mathbf{ }\sum _{k=1}^9(-2) = 9 \times -2 = - 18$

 

 

13) رياضة : تدرَّب مازن على الجري مسافات طويلة ، فركض في الدقائق الست الأولى مسافة 1000 m ، ثم ركض في كل ست دقائق لاحقة مسافة أقل ب 10 m من تلك التي ركضها في الدقائق الست السابقة لها. أكتب متسلسلة تُمثِّل المسافة التي ركضها مازن في 60 دقيقة.

الحل : 

المتسلسلة  : $1000 + 990 + 980 +970 + 960 + 950 + 940 + 930 + 920 + 910$

عدد الحدود  =  10   $(60 ÷ 6 = 10)$

المتسلسلة باستخدام رمز المجموع : $\sum _{k=1}^{10}(1010 - 10k)$

---

 

14) أكتب متسلسلة تُمثِّل مجموع المربعات بعد n مرحلة للشكل الآتي :

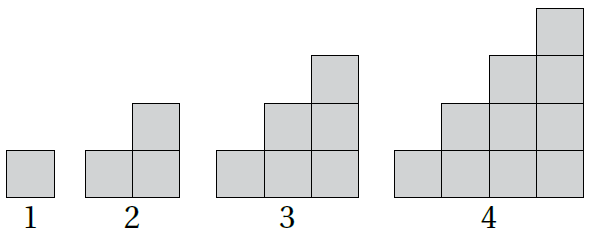
الحل : 

المتسلسلة باستخدام رمز المجموع  : $\sum _{k=1}^n\left(\frac{k (k+1)}{2}\right)$ 

---