المتتاليات والمتسلسلات
المتتاليات:
.
|
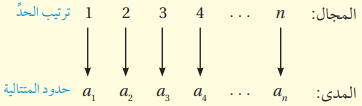
المتتالية اقتران مجاله مجموعة الأعداد الصحيحة الموجبة، أو مجموعة جزئية منها، ومداه مجموعة جزئية من مجموعة الأعداد الحقيقية، حيث يرتبط كل عدد صحيح في المجال بعدد صحيح في المدى، هو أحد حدود المتتالية.
حيث: : الحد الأول للمتتالية، و : الحد الثاني للمتتالية، و : الحد العام للمتتالية. |
ملاحظة: تكون المتتالية منتهية إذا حوت عددا منتهيا من الحدود وغير منتهية إذا حوت عددا لا نهائيا من الحدود.
مثال:
أجد الحدود الثلاثة الأولى لكل من المتتاليات الآتية:
ملاحظة: إذا كانت حدود المتتالية تتبع نمطا يمكن تعرفه فإنه يمكن إيجاد الحد العام للمتتالية () (أي إيجاد قاعدة النمط).
مثال:
أجد الحد العام لكل متتالية مما يأتي:
نلاحظ أن الحدود عبارة عن كسر مرفوعا كل مرة لقوة مختلفة.
نلاحظ أن حدود المتتالية هي عبارة عن الرقم (1) ويكون مرة موجبا ومرة سالبا.
المتسلسلات:
المتسلسلة هي مجموع حدود متتالية حيث يمكن إيجاد هذا المجموع بوضع إشارة الجمع (+) بين حدود المتتالية بدلا من الفواصل.
ملاحظة:
1) تكون المتسلسلة منتهية إذا حوت عددا منتهيا من الحدود وتكون المتسلسة غير منتهية إذا حوت عددا لا نهائيا من الحدود.
2) يمكن التعبير عن المتسلسلة بطريقة مختصرة باستعمال رمز المجموع () (يقرأ: سيغما) على النحو الآتي:
مثال:
أكتب كل متسلسة مما يأتي باستعمال رمز المجموع:
ملاحظة: يمكننا إيجاد مجموع متسلسلة منتهية بجمع حدودها فإذا كتبت المتسلسة باستعمال رمز المجموع فإننا نستعمل الحد العام لإيجاد حدودها ثم جمعها.
مثال:
أجد مجموع كل متسلسلة مما يأتي:
نعوض القيم k=1,2,3,4,5 في الحد العام للمتسلسلة وهو .
نعوض القيم k=1,2,3 في الحد العام للمتسلسلة.
مثال:
هندسة معمارية: صمم مهندس مبنى مكونا من 5 طوابق، أرضية كل منها على شكل مربع. إذا كان طول الضلع لأرضية الطابق الأول 30m، ونقص طول الضلع لأرضية كل طابق 2m عنه للطابق الذي يسبقه،فأجيب عما يأتي:
1) أكتب متسلسلة تمثل مجموع مساحة الأرضيات لطوابق المبنى باستعمال رمز المجموع.
أولا: ننشئ جدولا.
| الطابق | 1 | 2 | 3 | 4 | 5 |
| مساحة أرضية الطابق () | 900 | 784 | 676 | 576 | 484 |
ثانيا: نجد الحد العام للمتتالية
ثالثا: نستعمل رمز المجموع.
2) أجد مجموع مساحة الأرضيات لطوابق مبنى.
حالات خاصة من المتسلسلات:
هناك مجموعة من الخصائص المرتبطة برمز المجموع.
|
إذا كان و الحدين العامين للمتتاليتين، وكان c عددا حقيقيا، فإن:
|
أما إذا كان في المتسلسلة عدد كبير من الحدود فهناك قواعد يمكن استعمالها لإيجاد مجموع بعض المتسلسلات الخاصة بسهولة.
|
|
مثال:
أجد مجموع كل متسلسلة مما يأتي: