رياضيات فصل ثاني

أتحقق من فهمي

ص: 156

أجد الحدود الأربعة الأولى لكل من المتتاليات الآتية:

$a) a_n=\frac{n}{2n-1}$

$$\begin{gathered} a_1=\frac{1}{2\times 1-1} \\ {a}_2=\frac{2}{2\times 2-1}=\frac{2}{3} \\ {a}_3=\frac{3}{2\times 3-1}=\frac{3}{5} \\ {a}_4=\frac{4}{2\times 4-1}=\frac{4}{7} \end{gathered}$$

$b) a_n={(-2n)}^n$

$$\begin{gathered} a_1={(-2\times 1)}^1=-2 \\ {a}_2={(-2\times 2)}^2 \\ {a}_3={(-2\times 3)}^3=-216 \\ {a}_4={(-2\times 4)}^4=4096 \end{gathered}$$

$c) a_n=\left\{\begin{array}{l}2n , \mathrm{زوجي} \mathrm{عدد} n\\ n^2 , \mathrm{فردي} \mathrm{عدد} n\end{array}\right.$

$$\begin{gathered} a_1=1^2=1 \\ {a}_2=2\times 2=4 \\ {a}_3=3^2=9 \\ {a}_4=2\times 4=8 \end{gathered}$$

أتحقق من فهمي

ص: 156

أجد الحد العام لكل متتالية مما يأتي:

$a) \frac{1}{2}, \frac{3}{4}, \frac{5}{6}, \frac{7}{8}, ...$

$a_n=\frac{2n-1}{2n}$

$b) -3, 9, -27, 81, ...$

$a_n={(-3)}^n$

أتحقق من فهمي

ص: 157

أكتب كل متسلسة مما يأتي باستعمال رمز المجموع:

$a) 7+10+13+16+...+25$

$7+10+13+16+...+25=\sum _{k=1}^7 (3k+4)$

$b)1-2+3-4+...$

$1-2+3-4+...=\sum _{k=1}^{\infty } k{(-1)}^{k+1}$

أتحقق من فهمي

ص: 158

أجد مجموع كل متسلسة مما يأتي:

$a) \sum _{k=1}^7 \frac{5k-2}{2}$

$\frac{5\times 1-2}{2}+\frac{5\times 2-2}{2}+\frac{5\times 3-2}{2}+\frac{5\times 4-2}{2}+\frac{5\times 5-2}{2}+\frac{5\times 6-2}{2}+\frac{5\times 7-2}{2}=63$

$b) \sum _{k=1}^5 {(k+1)}^2$

${\left(1+1\right)}^2+{\left(2+1\right)}^2+{\left(3+1\right)}^2+{\left(4+1\right)}^2+{\left(5+1\right)}^2=90$

أتحقق من فهمي

ص: 159

مطاعم: يوجد في قاعة الطعام لأحد المطاعم طاولات على شكل شبه منحرف، وكراسي تحيط بها كما في الشكل الآتي:

أكتب باستعمال رمز المجموع متسلسلة يمثل مجموعها عدد الكراسي في المطعم، ثم أجد مجموع المتسلسلة.

$$\begin{gathered} n=1 / a_1=3\times 1+2=5 \\ n=2 / a_2=3\times 2+2=8 \\ n=3 / a_3=3\times 3+2=11 \\ 5+8+11=\sum _{k=1}^3 (3k+2)=24 \end{gathered}$$

أتحقق من فهمي

ص: 161

أجد مجموع كل متسلسلة مما يأتي:

$a) \sum _{k=1}^{10} 3k^2$

$$\begin{gathered} 3\sum _{k=1}^{10} k^2=3\frac{\left(10\right(10+1\left)\right(2\left(10\right)+1\left)\right)}{6} \\ =5\left(11\right)\left(21\right) \\ =1155 \end{gathered}$$

$b) \sum _{k=1}^{20}(7k-2)$

$$\begin{gathered} 7\sum _{k=1}^{20}-\sum _{k=1}^{20} 2 \\ 7\left(\frac{20(20+1)}{2}\right)-2\left(20\right) \\ =1470-40=1430 \end{gathered}$$

$c) \sum _{k=1}^5 (-4k^3)$

$$\begin{gathered} \sum _{k=1}^5 -4k^3=-900 \\ -4\sum _{k=1}^5 k^3=-4{\left(\frac{5(5+1)}{2}\right)}^2 \\ =-4{\left(15\right)}^2=-4\times 225 \\ =-900 \end{gathered}$$

أتدرب وأحل المسائل

أجد الحدود الأربعة الأولى لكل من المتتاليات الآتية:

$1) a_n=n^3-n$

$$\begin{gathered} a_1=1^3-1=0 \\ {a}_2=2^3-2=6 \\ {a}_3=3^3-3=24 \\ {a}_4=4^3-4=60 \end{gathered}$$

$2) a_n=9-3^n$

$$\begin{gathered} a_1=9-3^1=6 \\ {a}_2=9-3^2=0 \\ {a}_3=9-3^3=-18 \\ {a}_4=9-3^4=-27 \end{gathered}$$

$3) a_n=\frac{2^n}{3^n+1}$

$$\begin{gathered} a_1=\frac{2^1}{3^1+1}=\frac{1}{2} \\ {a}_2=\frac{2^2}{3^2+1}=\frac{2}{5} \\ {a}_3=\frac{2^3}{3^3+1}=\frac{2}{7} \\ {a}_4=\frac{2^4}{3^4+1}=\frac{8}{41} \end{gathered}$$

$4) a_n=\frac{n}{e^n}$

$$\begin{gathered} a_1=\frac{1}{e^1}=\frac{1}{e} \\ {a}_2=\frac{2}{e^2} \\ {a}_3=\frac{3}{e^3} \\ {a}_4=\frac{4}{e^4} \end{gathered}$$

$5) a_n=\frac{n-1}{n^2+n}$

$$\begin{gathered} a_1=\frac{1-1}{1^2+1}=0 \\ {a}_2=\frac{2-1}{2^2+2}=\frac{1}{6} \\ {a}_3=\frac{3-1}{3^2+3}=\frac{1}{6} \\ {a}_4=\frac{4-1}{4^2+4}=\frac{3}{20} \end{gathered}$$

$6) a_n={(-1)}^{n-1} (\frac{n}{2n-1})$

$$\begin{gathered} a_1={(-1)}^{1-1}\left(\frac{1}{2\times 1-1}\right)=1 \\ {a}_2={(-1)}^{2-1}\left(\frac{2}{2\times 2-1}\right)=-\frac{2}{3} \\ {a}_3={(-1)}^{3-1}\left(\frac{3}{2\times 3-1}\right)=\frac{3}{5} \\ {a}_4={(-1)}^{4-1}\left(\frac{4}{2\times 4-1}\right)=-\frac{4}{7} \end{gathered}$$

أجد الحد العام لكل متتالية مما يأتي:

$7) -\frac{1}{3}, \frac{1}{4},-\frac{1}{5},\frac{1}{6},...$

$a_n={(-1)}^n\frac{1}{n+2}$

$8) 3,\frac{9}{4},\frac{27}{9},\frac{81}{16},...$

$a_n=\frac{3^n}{n^2}$

$9) 1,\frac{1}{2},3,\frac{1}{4},5,\frac{1}{6},...$

$a_n=\left\{\begin{array}{l}n, n\mathrm{فردي}\\ \frac{1}{n} , n\mathrm{زوجي}\end{array}\right.$

$10) 58,-25,125,-625,...$

$a_n={(-1)}^{n-1} {\left(5\right)}^n$

$11) 1,-1,1,-1,1,... ..$

$a_n={(-1)}^{n-1}$

$12) \frac{1}{10},\frac{3}{20}.\frac{5}{30},\frac{7}{40},... .$

$a_n=\frac{2n-1}{10n}$

أعمدة إنارة: وضعت أعمدة إنارة في نهاية كل 100m على امتداد طريق سريع، كما في الشكل الآتي:

13) أجد الحد العام للمتتالية التي تمثل عدد أعمدة الإنارة على الطريق السريع.

$$\begin{gathered} 4,6,8 \\ {a}_1=2\times 1+2 \\ {a}_2=2\times 2+2 \\ {a}_3=2\times 3+2 \\ {a}_n=2n+2 \end{gathered}$$

14) أجد عدد أعمدة الإنارة على طريق طوله 8km.

$$\begin{gathered} n=\frac{8\times 1000}{100} \\ n=80 \\ {a}_{80}=2\times 80+2 \\ =160+2=162 \end{gathered}$$

162 عامودا

أكتب كل متسلسة مما يأتي باستعمال رمز المجموع:

$15) 1+4+9+.....+100$

$\sum _{k=1}^{10} k^2$

$16) 2+4+6+....+20$

$\sum _{k=1}^{10} 2k$

$17) \frac{1}{2}+\frac{2}{3}+\frac{3}{4}+...+\frac{13}{14}$

$\sum _{k=1}^{13} \frac{k}{k+1}$

$18) -\frac{2}{3}+\frac{4}{9}-\frac{8}{27}+...+\frac{64}{729}$

$\sum _{k=1}^6 {\left(\frac{-2}{3}\right)}^k$

$19) \frac{1}{2 \ln 2}-\frac{1}{3 \ln 3}+\frac{1}{4 \ln 4}-\frac{1}{5 \ln 5}+...+\frac{1}{100 \ln 100}$

$\sum _{k=1}^{10} \frac{{(-1)}^{k+1}}{(k+1) ln (k+1)}$

أجد مجموع كل متسلسلة مما يأتي:

$20) \sum _{n=1}^6 {(-2)}^n$

$$\begin{gathered} {(-2)}^1+{(-2)}^2+{(-2)}^3+{(-2)}^4+{(-2)}^5+{(-2)}^6 \\ -2+4-8+16-32+64 \\ =42 \end{gathered}$$

$21) \sum _{n=1}^4 \frac{n^2+1}{n+1}$

$$\begin{gathered} \sum _{n=1}^4 \frac{n^2+1}{n+1}=\frac{257}{30} \\ \frac{1^2+1}{1+1}+\frac{2^2+1}{2+1}+\frac{3^2+1}{3+1}+\frac{4^2+1}{4+1} \\ 1+\frac{5}{3}+\frac{10}{4}+\frac{17}{5}=\frac{257}{30} \end{gathered}$$

$22) \sum _{n=1}^2 \frac{1}{3^n+1}$

$$\begin{gathered} \sum _{n=1}^2 \frac{1}{3^n+1}=\frac{7}{20} \\ \frac{1}{3^1+1}+\frac{1}{3^2+1} \\ \frac{1}{4}+\frac{1}{7}=\frac{7}{20} \end{gathered}$$

$23) \sum _{k=1}^6 \frac{k^2}{2}$

$$\begin{gathered} \sum _{k=1}^6 \frac{k^2}{2}=\frac{91}{2} \\ \frac{1^2}{2}+\frac{2^2}{2}+\frac{3^2}{2}+\frac{4^2}{2}+\frac{5^2}{2}+\frac{6^2}{2} \\ \frac{1}{2}+2+\frac{9}{2}+8+\frac{25}{2}+18=\frac{91}{2} \end{gathered}$$

$24) \sum _{k=1}^9 (12k-24)$

$$\begin{gathered} 12\sum _{k=1}^{9}k-\sum _{k=1}^{9}24 \\ 12\left(\frac{9\times 10}{2}\right)-24\times 9=324 \end{gathered}$$

$25) \sum _{k=1}^{20} (k^3-1)$

$$\begin{gathered} \sum _{k=1}^{20}{k}^3-\sum _{k=1}^{20} 1 \\ ={\left(\frac{20\times 21}{2}\right)}^2-1\times 20=44080 \end{gathered}$$

26) يمارس هيثم تمارين الضغط بانتظام، وقد استطاع أداء 25 ضغطة بصورة مستمرة في الأسبوع الأول، ثم تمكن من زيادة عددها أسبوعيا بمقدار 5 ضغطات على نحو مستمر. ما عدد الضغطات التي يمكنه أداؤها بشكل مستمر بعد 16 أسبوعا؟

$$\begin{gathered} a_n=25+5(n-1) \\ {a}_{16}=25+5(16-1) \\ =25+5\times 15=100 \end{gathered}$$

بعد 16 أسبوع يمكنه اداء: 100+5=105 ضغطة

27) فنون: بنى جمال منزلا من أوراق اللعب مشابها للمنزل المجاور. من كم صفا يتكون منزل جمال إذا كان لديه 40 ورقة لعب؟

الصف الأول 3

الصف الثاني 6

الصف الثالث 9

الصف الرابع 12

الصف الخامس 10=5-15

40=3+6+9+12+10

عدد الصفوف 5

28) أحل المسألة الواردة في بند (مسألة اليوم).

19=10+6+3

مهارات التفكير العليا

29) تبرير: هل للمتسلسلتين: 9+7+5+3+1 و 1+3+5+7+9 المجموع نفسه؟ هل يمكن التعبير عنهما بالطريقة نفسها باستعمال رمز المجموع؟ أبرر إجابتي.

لهما المجموع نفسه لأن الجمع عملية تبديلية.

أما عند كتابتهما بصيغة المجموع فيكتبان بطريقتين مختلفتين لأنه يجب مراعاة ترتيب الحدود.

$$\begin{gathered} 1+3+5+7+9=\sum _{k=1}^5 (2k-1) \\ 9+7+5+3+1=\sum _{k=1}^5 (11-2k) \end{gathered}$$

30) تحد: أجد الحد العام للمتتالية الآتية: ...,2,4,10,28

$a_n=1+3^{n-1}$

31) تحد: أجد الحد العام للمتتالية الآتية: $\sqrt{2} , \sqrt{2\sqrt{2}} , \sqrt{2\sqrt{2\sqrt{2}}} , \sqrt{2\sqrt{2\sqrt{2\sqrt{2}}}} , ...$.

$$\begin{gathered} 2^{\frac{1}{2}} , 2^{\frac{3}{4}} , 2^{\frac{7}{8}} , 2^{\frac{15}{16}} , ... \\ {a}_n=2^{\frac{2^n-1}{2^n}} \end{gathered}$$

حل أسئلة كتاب التمارين

أجد الحدود الأربعة الأولى لكل من المتتاليات الآتية:

$1) a_n={(-\frac{1}{2})}^{n-1}$

$a_1=1 , a_2=-\frac{1}{2}, a_3=\frac{1}{4} , a_4=-\frac{1}{8}$

$2) a_n=-3n^2$

$a_1=-3 , a_2=-12 , a_3=-27 , a_4=-48$

$3) a_n={(n+1)}^2$

$a_1=4 , a_2=9 , a_3=16 , a_4=25$

$4) a_n=n(n-1)$

$a_1=0 , a_2=2 , a_3=6 , a_4=12$

$5) a_n=1+{(-1)}^n$

$a_1=0 , a_2=2 , a_3=0 , a_4=2$

$6) a_n=n^n$

$a_1=1 , a_2=4 , a_3=27 , a_4=64$

أكتب كلا مما يأتي من دون استعمال رمز المجموع:

$7) \sum _{k=1}^5 \sqrt{k}$

$1+\sqrt{2}+\sqrt{3}+2+\sqrt{5}$

$8) \sum _{k=1}^9 k(k+3)$

$4+10+18+28+40+54+70+88+108$

$9) \sum _{k=1}^4 \frac{2k-1}{2k+1}$

$\frac{1}{3}+\frac{3}{5}+\frac{5}{7}+\frac{7}{9}$

معتمدا الشكل المجاور الذي يمثل نمطا هندسيا، أجيب عن كل مما يأتي:

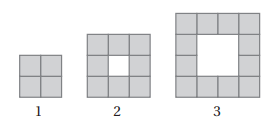
10) أكتب الحد العام للمتتالية التي تمثل عدد المربعات الملونة في كل شكل.

$a_n=4n$

11) أكتب باستعمال رمز المجموع متسلسلة يمثل مجموعها عدد المربعات الملونة في أول عشرين شكل من هذا النمط، ثم أجد مجموع المتسلسلة.

$\sum _{k=1}^{20} 4k=840$

12) اذا كان طول ضلع كل مربع ملون هو وحدة واحدة، فأجد الحد العام للمتتالية التي تمثل مساحة المربعات البيضاء، وسط كل شكل.

$a_n={(n-1)}^2$

أكتب كل متسلسلة مما يأتي باستعمال رمز المجموع:

$13) -1+4-9+...+36$

$\sum _{k=1}^6 k^2{(-1)}^k$

$14) 10.8+10.5+10.2+9.9$

$\sum _{k=1}^4 (11.1-0.3k)$

$15) 3+\frac{3}{2}+1+\frac{3}{4}+...+\frac{3}{8}$

$\sum _{k=1}^8 \frac{3}{k}$

$16) 1000+100+10+...+\frac{1}{100}$

$\sum _{k=1}^6 1000 {\left(\frac{1}{10}\right)}^{k-1}$