رياضيات فصل ثاني

تعاملنا سابقًا مع النقاط والمستقيمات والمنحنيات في المستوى الإحداثي ، وهو مستوى ذو بعدين : x و y .

ولدراسة النقاط في الفضاء ، يلزمنا إضافة محور ثالث ، المحور z ، يعامد المستوى الإحداثي المستوى xy ، فيصبح لدينا (نظام الإحداثيات

ثلاثي الأبعاد). والذي يمكننا من التعامل مع النقاط في الفضاء.

فالمحاور الثلاثة : المحور x ، والمحور y ، والمحور z ، محاور متعامدة ، تتقاطع معًا في نقطة الأصل . ويمكن تعيين أي نقطة في الفضاء عن

طريق ثلاثي مرتب $p(x,y,z)$.

وينتج من تقاطع كل محورين، مستوى يحويهما هي: المستوى xy والمستوى xz والمستوى yz ، والتي تقسم الفضاء إلى ثمن أجزاء يسمى

كل منها ثمناً .

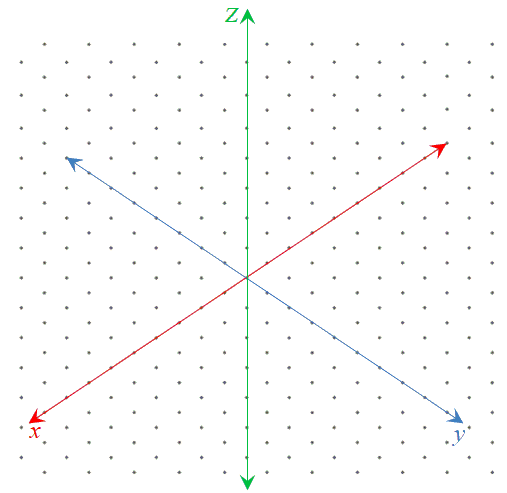
ولتعيين النقطة $p(a,b,c)$ في نظام الإحداثيات ثلاثي الأبعاد :

أولاً : نعين النقطة $(a,b)$ في المستوى xy .

ثانياً: ثم نتحرك إلى الأعلى (إذا كانت c موجبة) أو إلى الأسفل (إذا كانت c سالبة) مسافة |c| لتحديد النقطة p.

ويمكن الاستعانة بالورق المنقط في عملية التمثيل .

عيّن النقطة $(3,1,4)$ التالية في نظام الإحداثيات ثلاثي الأبعاد: 

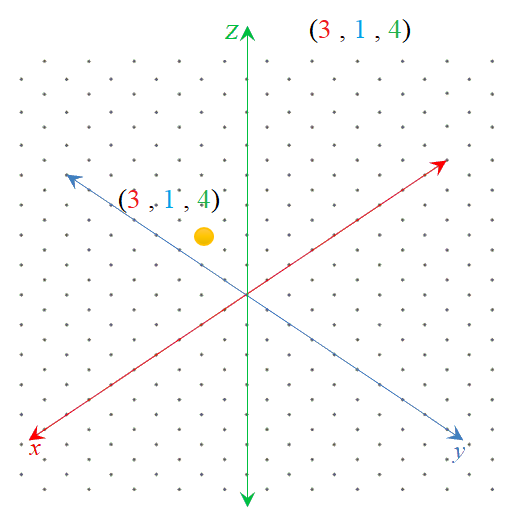
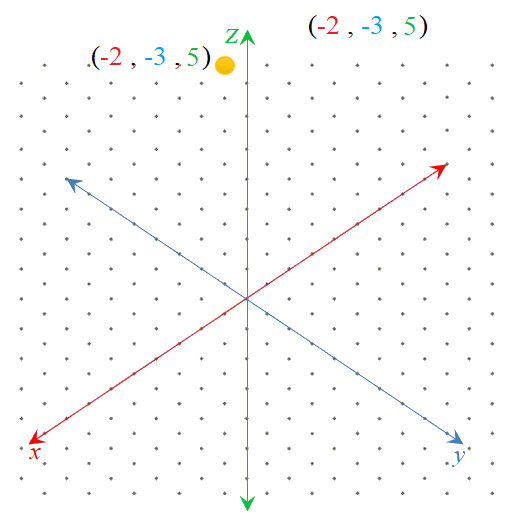
عيّن النقطة $\left(-2, -3 , -5\right)$ التالية في نظام الإحداثيات ثلاثي الأبعاد: 

يمكن تعميم صيغة المسافة بين نقطتين في المستوى ، وإحداثيات نقطة المنتصف ، للحصول على الصيغة التالية:

إذا كانت $B(x_2,y_2,z_2) و A(x_1,y_1,z_1)$ نقطتين في الفضاءفإن:

أولاً:  المسافة بين النقطتين A و B هي:

$AB=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2+{(z_2-z_1)}^2}$

ثانياً:  احداثيات نقطة من منتصف القطعة المستقيمة  $\overline{AB}$ هي: 

$M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2},\frac{z_1+z_2}{2})$

إذا كانت: $B(4,2,-1) , A(3,-1,4)$ فجد:

أولاً:  المسافة بين A و B

الحل:

$$\begin{gathered} AB=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2+{(z_2-z_1)}^2} \\ =\sqrt{{(4-3)}^2+{(2+1)}^2+{(-1-4)}^2} \\ AB=\sqrt{35} \end{gathered}$$

ثانياً:  إحداثيات نقطة منتصف  $\overline{ AB }$

         $$\begin{gathered} Solution: \\ M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2},\frac{z_1+z_2}{2})=M(\frac{4+3}{2},\frac{2+-1}{2},\frac{-1+4}{2}) \\ M(\frac{7}{2},\frac{1}{2},\frac{3}{2}) \end{gathered}$$

 

 

لا بد من دراسة المتجهات في الفضاء ، لأن كثيرًا من الكميات الفيزيائية هي كميات متجهة (مثل الإزاحة والسرعة).

ونرمز للمتجه بإحدى الطريقتين التاليتين:

أولاً:  حرف غامق فوقه الرمز $\rightharpoonup$  مثل المتجه:  $\stackrel{\mathbf{\rightharpoonup }}{\mathbf{ }\mathit{v}\mathbf{ }}$

ثانياً: حرفان (نقطة البداية A ، ونقطة النهاية B) فوقهما الرمز $\rightharpoonup$ مثل المتجه $\stackrel{\rightharpoonup }{ AB }$

والذي يمكن تمثيله في الإحداثيات ثلاثية الأبعاد كما يلي:

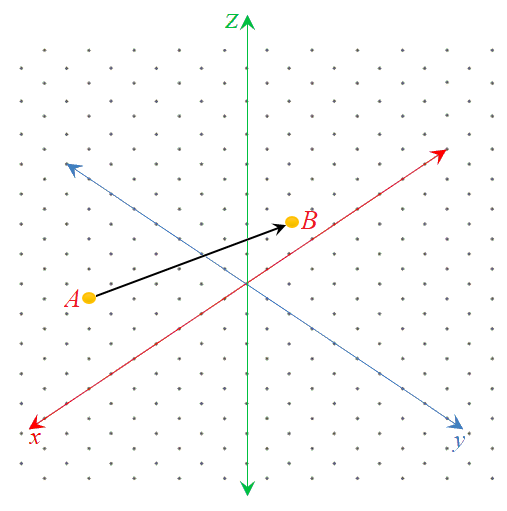
ويمكن كتابة المتجه بالصورة الإحداثية عن طريق طرح الإحداثيات للحصول على إحداثيات المتجه وهي $V_1 , V_2 , V_3$  بالصيغة:

_{$$\begin{gathered} \stackrel{\rightharpoonup }{\mathit{v}}=\stackrel{\rightharpoonup }{AB}=<x_2-x_1,y_2-y_1,z_2-z_1> \\ =<v_1,v_2,v_3> \end{gathered}$$}

حيث تمثل إحداثيات المتجه   $\stackrel{\rightharpoonup }{ V }$ مقدار الإزاحة بالنسبة إلى المحور المناظر فمثلا $V_1$ يمثل مقدار الإزاحة بالنسبة للمحور x وهكذا.

ويتم حساب مقدار المتجه (طول المتجه) (ويرمز له بالرمز  $\left|\stackrel{\rightharpoonup }{ AB }\right|$ أو $\left|\stackrel{\rightharpoonup }{\mathbf{ }\mathit{v}\mathbf{ }}\right|$ ) عن طريق صيغة المسافة بين نقطتين كالتالي:

 

$$\begin{gathered} \left|\stackrel{\rightharpoonup }{AB}\right|=\left|\stackrel{\rightharpoonup }{\mathit{v}}\right|=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2+{(z_2-z_1)}^2} \\ =\sqrt{v_1^2+v_2^2+v_3^2} \end{gathered}$$

جد مقدار المتجه  $\stackrel{\rightharpoonup }{ MN }$ حيث:$N(-3,1,4) , M(-1,4,2)$

الحل:

$$\begin{gathered} Solution: \\ \stackrel{\rightharpoonup }{ MN }=<-3+1,1-4,5-2> \\ =<-2,-3,3> :\mathrm{الإحداثية} \mathrm{الصورة} \\ \left|\stackrel{\rightharpoonup }{ MN }\right|=\sqrt{{(-2)}^2+{(-3)}^2+{\left(3\right)}^2}=\sqrt{22} \end{gathered}$$

أولاً : جمع المتجهات:  

لاحظ الشكلين التاليين:

ثانياً : طرح المتجهات:  

لاحظ الشكلين التاليين:

ثالثاً : ضرب المتجهات في عدد حقيقي: $R\stackrel{\rightharpoonup }{ v }$(حيث R عدد حقيقي):

هو متجه ، يوازي المتجه  $\stackrel{\rightharpoonup }{\mathit{v}}$ وطوله يساوي |R| مضروباً في طول  $\stackrel{\rightharpoonup }{\mathit{v}}$,

وسيكون في نفس الإتجاه الأصلي إذا كان $R>0$ ، وفي عكس الإتجاه إذا كان $R<0$  لاحظ الشكل التالي:

 

في المثلث $ABC$:

إذا كانت E منتصف $\stackrel{\rightharpoonup }{AB}=6\stackrel{\rightharpoonup }{n},\stackrel{\rightharpoonup }{CD}=4\stackrel{\rightharpoonup }{m}،DB = 2CD،\overline{AC}$ ،  فجد $\stackrel{\rightharpoonup }{AE }$ بدلالة  $\stackrel{\rightharpoonup }{ n }, \stackrel{\rightharpoonup }{ m }$

الحل:

 لاحظ الشكل أعلاه:

$$\begin{gathered} \stackrel{\rightharpoonup }{AE}=\frac{1}{2}\stackrel{\rightharpoonup }{AC} \mathrm{سنجد} \\ \stackrel{\rightharpoonup }{AC}=\stackrel{\rightharpoonup }{AB}+\stackrel{\rightharpoonup }{BC} \\ =\stackrel{\rightharpoonup }{AB}+-\stackrel{\rightharpoonup }{CB} \\ =6\stackrel{\rightharpoonup }{n}+-(CD+DB) \\ =6\stackrel{\rightharpoonup }{n}+-(4\stackrel{\rightharpoonup }{m}+8\stackrel{\rightharpoonup }{m}) \\ \stackrel{\rightharpoonup }{AC}=6\stackrel{\rightharpoonup }{n}-12\stackrel{\rightharpoonup }{m} \\ \stackrel{\rightharpoonup }{DB}=2\stackrel{\rightharpoonup }{CD} \mathrm{لأن}) \\ \stackrel{\rightharpoonup }{DB}=2(4\stackrel{\rightharpoonup }{m}) \\ \stackrel{\rightharpoonup }{DB}=8\stackrel{\rightharpoonup }{m} \\ \stackrel{\rightharpoonup }{AE}=\frac{1}{2}\stackrel{\rightharpoonup }{AC} \\ =\frac{1}{2}(6\stackrel{\rightharpoonup }{n}-12\stackrel{\rightharpoonup }{m}) (\stackrel{\rightharpoonup }{AC} \mathrm{منتصف} E) \\ =3\stackrel{\rightharpoonup }{n}-6\stackrel{\rightharpoonup }{m} \end{gathered}$$

يمكن اجراء عمليتي جمع وطرح المتجهات جبريًا، بجمع أو طرح الإحداثيات المتناظرة ، وكذلك ضربه في عدد حقيقي ،

بضرب الاحداثيات في هذا العدد كما يلي:

إذا كان:  $\stackrel{\rightharpoonup }{v}=<v_1,v_2,v_3>,\stackrel{\rightharpoonup }{w}=<w_1,w_2,w_3>$  ، R عدد حقيقي فإن:

$$\begin{gathered} \stackrel{\rightharpoonup }{v}+\stackrel{\rightharpoonup }{w}=<v_1+w_1,v_2+w_2,v_3+w_3> \\ \stackrel{\rightharpoonup }{v}-\stackrel{\rightharpoonup }{w}=<v_1-w_1,v_2-w_2,v_3-w_3> \\ R\stackrel{\rightharpoonup }{v}=<R{v}_1, R{v}_2, R{v}_3> \end{gathered}$$

إذا كان:   $\stackrel{\rightharpoonup }{b}=<-1,2,7> , \stackrel{\rightharpoonup }{a}=<4,-2,3>$ ،  فجد:

$$\begin{gathered} 1)\stackrel{\rightharpoonup }{b}+3\stackrel{\rightharpoonup }{a} \\ Solution: \\ \stackrel{\rightharpoonup }{b}+3\stackrel{\rightharpoonup }{a}=<-1,2,7>+3<4,-2,3> \\ =<11,-4,16> \\ 2)2\stackrel{\rightharpoonup }{a}-3\stackrel{\rightharpoonup }{b} \\ Solution: \\ 2\stackrel{\rightharpoonup }{a}-3\stackrel{\rightharpoonup }{b}=2<4,-2,3>-3<-1,2,7> \\ =<8,-4,6>+<3,-6,-21> \\ =<11,-10,-15> \\ 3\left)\frac{1}{2}\right(\stackrel{\rightharpoonup }{a}+2\stackrel{\rightharpoonup }{b}) \\ Solution: \\ \frac{1}{2}(\stackrel{\rightharpoonup }{a}+2\stackrel{\rightharpoonup }{b})=\frac{1}{2}(<4,-2,3>+2<-1,2,7>) \\ =\frac{1}{2}<2,2,17>=<1,1,\frac{17}{2}> \end{gathered}$$

يتساوى المتجهان $\stackrel{\rightharpoonup }{v}،\stackrel{\rightharpoonup }{w}$  ، إذا وفقط إذا كانت الإحداثيات المتناظرة لهما متساوية:

فإذا  كان :$\stackrel{\rightharpoonup }{w}=<w_1,w_2,w_3> , \stackrel{\rightharpoonup }{v}=<v_1,v_2,v_3>$

فإن $\stackrel{\rightharpoonup }{v}=\stackrel{\rightharpoonup }{w}$ إذا وفقط إذا كان $v_1=w_1 , v_2=w_2 , v_3=w_3$

إذا كان: $\stackrel{\rightharpoonup }{n}=<a+b,a+1, R> , \stackrel{\rightharpoonup }{m}=<1,-3,5>$ و كان $\stackrel{\rightharpoonup }{n}=2\stackrel{\rightharpoonup }{m}$ ، فجد كلا من الثوابت a,b,R.

$$\begin{gathered} Solution: \\ \stackrel{\rightharpoonup }{n}=2\stackrel{\rightharpoonup }{m} \\ <a+b,a+1,R>=<2,-6,10> \\ a+b=2 و a+1=-6 و R=10 \\ -7+b=2 | a=-7 | b=9 \end{gathered}$$

إذا كانت O هي نقطة الأصل $B\left(x_2, y_2 , z_2 \right) , A\left(x_1, y_1 , z_1\right)$ فإن:  
متجه الموقع: $\stackrel{\rightharpoonup }{OA }$ هو المتجه الذي يبدأ بنقطة الأصل وينتهي بالنقطة A.

متجه الموقع: $\stackrel{\rightharpoonup }{OB }$ هو المتجه الذي بدايته نقطة الأصل ونهايته النقطة B.

متجه الإزاحة: $\stackrel{\rightharpoonup }{AB }$ من النقطة A إلى النقطة B. ويكون:

$$\begin{gathered} \stackrel{\rightharpoonup }{OA}=<x_1,y_1,z_1>-<0,0,0>=<x_1,y_1,z_1> \\ \stackrel{\rightharpoonup }{OB}=<x_2,y_2,z_2>-<0,0,0>=<x_2,y_2,z_2> \\ \stackrel{\rightharpoonup }{AB}=\stackrel{\rightharpoonup }{OB}-\stackrel{\rightharpoonup }{OA}=<x_2-x_1,y_2-y_1,z_2-z_1> \end{gathered}$$

لاحظ أن: الموقع والإزاحة كميتان متجهتان ، أما المسافة فهي كمية قياسية ،

فالمسافة بين النقطتين A و B هي قيمة مقدار (طول) المتجه $\stackrel{\rightharpoonup }{AB }$.

إذا كانت: $Q(2,0,-8), P(1,2,-4)$ فجد: 

أولاً: متجه الموقع $\stackrel{\rightharpoonup }{OP }$

$$\begin{gathered} Solution: \\ \stackrel{\rightharpoonup }{OP}=<1,2,-4> \end{gathered}$$

ثانياً: متجه الإزاحة من النقطة Q إلى النقطة P.

          $$\begin{gathered} Solution: \\ \stackrel{\rightharpoonup }{PQ}=OQ-OP \\ =<2,0,-8>-<1,2,-4> \\ =<1,-2,-4> \end{gathered}$$

ثالثاً : المسافة بين النقطة Q و النقطة P

$$\begin{gathered} Solution: \\ \left|\stackrel{\rightharpoonup }{PQ}\right|=\sqrt{{\left(1\right)}^2+{(-2)}^2+{(-4)}^2} \\ =\sqrt{21} \mathrm{طول} \mathrm{وحدة} \end{gathered}$$

متجهات الوحدة الأساسية هي:

في اتجاه المحور x الموجب:  $\widehat{i }=<1,0,0>$

في اتجاه المحور y الموجب:  $\hat{j}=<0,1,0>$

في اتجاه المحور z الموجب:  $\hat{k}=<0,0,1>$

لاحظ الشكل التالي:

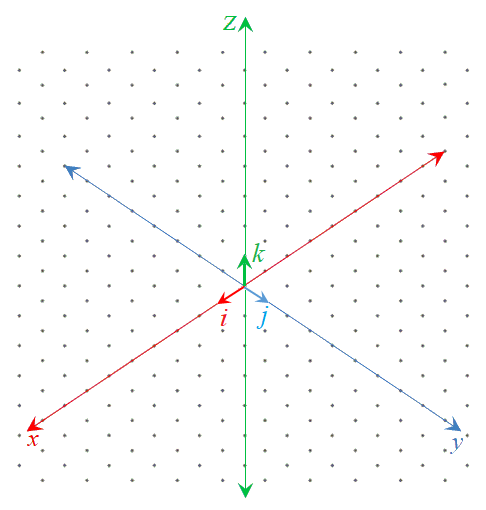
ونعبر عن متجه الوحدة (طوله وحدة واحدة) في اتجاه المتجه $\stackrel{\rightharpoonup }{v}$  بالرمز $\hat{v}$  ويُقرأ  v hat.

لذلك يمكن كتابة المتجه   $\stackrel{\rightharpoonup }{v}=<v_1,v_2,v_3>$ بدلالة متجهات الوحدة الأساسية بالصورة : $\stackrel{\rightharpoonup }{v}=v_1\hat{i}+v_2 \hat{j}+v_3\hat{k}$

و يمكن إيجاد متجه الوحدة في اتجاه أي متجه ، عن طريق قسمة هذا المتجه على مقدار المتجه ، أي أن: $\hat{v}=\frac{\stackrel{\rightharpoonup }{v}}{\left|\stackrel{\rightharpoonup }{v}\right|}$

إذا كان: $\stackrel{\rightharpoonup }{b}=3\hat{i}+4\hat{k} , \stackrel{\rightharpoonup }{a}=<1,-4,5>$

أولاً: اكتب   $\stackrel{\rightharpoonup }{a}$ بدلالة متجهات الوحدة الأساسية:

$$\begin{gathered} Solution: \\ \stackrel{\rightharpoonup }{a}=\hat{i}-4\hat{j}+5\hat{k} \end{gathered}$$

ثانياً: جد   $3\stackrel{\rightharpoonup }{a}-4\stackrel{\rightharpoonup }{b}$ بدلالة متجهات الوحدة الأساسية:

$$\begin{gathered} Solution: \\ 3\stackrel{\rightharpoonup }{a}-4\stackrel{\rightharpoonup }{b}=3(\hat{i}-4\hat{j}+5\hat{k})-4(3\hat{i}+4\hat{k}) \\ =-9\hat{i}-12\hat{j}-\hat{k} \end{gathered}$$

ثالثاً: متجه الوحدة في اتجاه المتجه $\stackrel{\rightharpoonup }{b}$

$$\begin{gathered} Solution: \\ \hat{b}=\frac{\stackrel{\rightharpoonup }{b}}{\left|\stackrel{\rightharpoonup }{b}\right|}=\frac{3\hat{i}+4\hat{k}}{\sqrt{3^2+4^2}} \\ =\frac{3}{5}\hat{i}+\frac{4}{5}\hat{k} \end{gathered}$$