رياضيات فصل ثاني

المتجهات في المستوى الإحداثي 

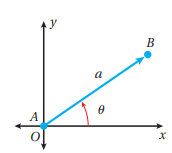
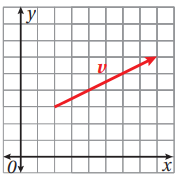
درست في الفيزياء، تمثيل المتجهات في صورة سهم ينطلق من نقطة إسناد ، مثل نقطة الأصل ، وبطول يحدده مقياس رسم مناسب ، واتجاهه تحدده الزاوية  θ التي يصنعها السهم مع محور مرجعي ، مثل محور x الموجب عكس عقارب الساعة . و لأن استعمال مقياس الرسم قد لا يكون دقيقا في بعض الأحيان، فإنه يتعين استعمال طريقة أكثر دقة لتمثيل  المتجهات . 

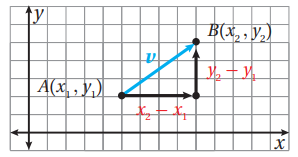
• يمكن تمثيل المتجه $\left( \stackrel{\rightharpoonup }{AB}\right)$في المستوى الإحداثي في صورة قطعة مستقيمة تمتد من نقطة بدايته $A \left( x_{1 } , y_1\right)$ إلى نقطة نهايته $B \left( x_{2 } , y_2\right)$ وفي اتجاه يحدده رمز السهم كما في الشكل ادناه .

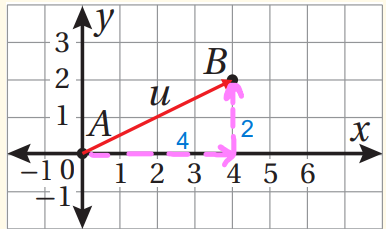
• تسمى المسافة الأفقية بين نقطة بداية المتجه ونقطة نهايته المركبة الأفقية و تساوي $\left( x_2 - x_1\right)$
• وتسمى المسافة الرأسية بينهما المركبة الرأسية  وتساوي $\left( y_2 - y_1\right)$
• يمكن كتابة المتجه بالصورة الإحداثية بدلالة مركبته الأفقية والرأسية ( العمودية ) كما يأتي :

$\mathit{v}\mathbf{ }\mathbf{=}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{AB}}\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }<x_2 - x_{1 } , y_2 - y_1 >\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }<a , b >$

 

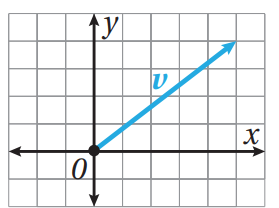
• إذا كانت نقطة بداية المتجه هي نقطة الأصل 0 ، كما في الشكل أدناه ، فإنه يكون في الوضع القياسي . 

مثال 

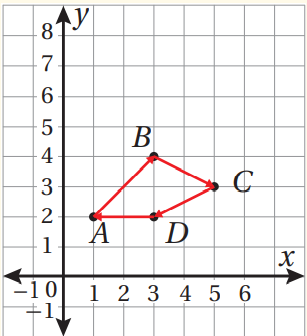
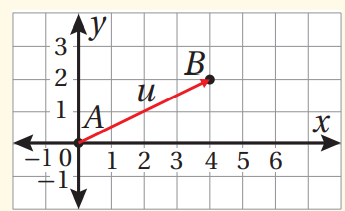
اعتمادا على الشكل الآتي ، اكتب المتجهات الآتية بالصورة الإحداثية : 

$\mathbf{1}\mathbf{.}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{A}\mathbf{B}}$

نقطة بداية المتجه $\left( x_1 , y_1\right)$ = A( 1 , 2)   ونقطة نهايته هي $\left(x_{2 , } y_2\right)$ = B ( 3 , 4 ) 

المركبة الأفقية 

$x_{2 } - x_1 = 3- 1 = 2$

المركبة الرأسية 

$y_{2 } - y_1 = 4 - 2 = 2$

إذا 

$\mathbf{2}\mathbf{.}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{B}\mathbf{C}}$

المركبة الأفقية 

x₂ - x₁  = 5 - 3 = 2

المركبة الرأسية  

y₂ - y₁ = 3 -4 = -1 

$\mathbf{3}\mathbf{.}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{C}\mathbf{D}}$

 

المركبة الأفقية 

x₂ - x₁  =  3 - 5  = -2

المركبة الرأسية  

y₂ - y₁ = 2 -3 = -1

 

$\mathbf{4}\mathbf{.}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{D}\mathbf{A}}$

المركبة الأفقية 

x₂ - x₁  = 1 -3  = -2 

المركبة الرأسية  

y₂ - y₁ = 2 - 2 = 0

---

• مقدار المتجه هو كمية قياسية تمثل طول القطعة المستقيمة الواصلة بين نقطتي بداية المتجه ونهايته .

فإذا كانت P₁ ( x₁ , y₁ ) هي نقطة بداية v  و P₂ ( x₂ , y₂ )  هي نقطة نهايته ، فإنه يمكن استعمال نظرية فيثاغورس لإيجاد الصيغة الآتية لمقدار المتجه $\left|v\right|$ : 

$\left|v\right|\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{ }{\left( x_{2 } - x_1\right)}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(y_2 - y_1\right)}^{\mathbf{2}\mathbf{ }}}$

 

مفهوم  أساسي :

مقدار المتجه : 

إذا كانت P₁ ( x₁ , y₁ ) هي نقطة بداية v  و P₂ ( x₂ , y₂ )  هي نقطة نهايته ، فإنه يمكن إيجاد  مقدار المتجه $\left|v\right|$  باستعمال الصيغة الآتية : 

$\left|v\right|\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{ }{\left(x_2 - x_1\right)}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }{\left( y_2 - y_1\right)}^{\mathbf{2}}}$

 و إذا كان المتجه v مكتوبا بالصورة الإحداثية  v = ( a , b)  ، فإنه يمكن إيجاد مقداره باستعمال الصيغة الآتية :

$\left|v\right|\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{ }{\mathbf{a}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{b}}^{\mathbf{2}}}$

 

مثال 

1 . أجد مقدار المتجه v  في الشكل التالي : 

نحدد إحداثيات كل من نقطة بداية المتجه ونقطة نهايته .

نقطة البداية  ( 3 , 2 ) 

نقطة النهاية ( 6 , 8 ) 

ثم نعوض الإحداثيات في صيغة مقدار المتجه 

$$\begin{gathered} \left|v\right| = \sqrt{ {\left(x_2 - x_1\right)}^2 + {\left( y_{2 } - y_1\right)}^2} \\ = \sqrt{ {\left(8 - 2\right)}^2 + {\left( 6 -3 \right)}^2} \\ = \sqrt{ 36 +9} \\ = 3\sqrt{5} \end{gathered}$$

1 . أجد مقدار المتجه

$$\begin{gathered} \left| \stackrel{\rightharpoonup }{AB}\right|\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{ }{\mathbf{a}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{b}}^{\mathbf{2}}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{ }{\mathbf{4}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{-}\mathbf{3}\mathbf{)}}^{\mathbf{2}}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{16}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{9}\mathbf{ }}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{25}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{5} \end{gathered}$$

---

• يمكن استعمال النسب المثلثية لإيجاد اتجاه المتجه ، وذلك باستعمال المثلث قائم الزاوية الذي يمثل المتجه وترا فيه.

 

مثال

أجد اتجاه $\stackrel{\rightharpoonup }{AB}$  في الشكل الآتي : 

 

نستعمل نسبة الظل في المثلث قائم الزاوية الذي يمثل u وترا فيه 

$$\begin{gathered} tan \theta =\frac{y}{x } \\ = \frac{2}{4} \\ = \frac{1}{2} \end{gathered}$$

باستعمال معكوس الظل 

$\mathit{\theta }\mathbf{ }\mathbf{=}\mathbf{ }\mathit{t}\mathit{a}\mathit{n}{\mathbf{ }}^{\mathbf{-}\mathbf{1}}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{26}\mathbf{.}{\mathbf{6}}^{\mathbf{\circ }}$

$\mathbf{26}\mathbf{.}\mathbf{6}\mathbf{°}$  مع محور x  الموجب 

---

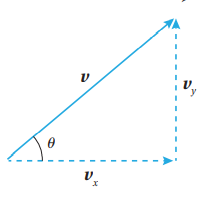
• ​​​​​​​السرعة المتجهة هي سرعة في اتجاه محدد ويمكن تمثيلها بمتجه. في الشكل اللآتي ، يمثل المتجه v  السرعة المتجهة لجسم تحرك في مسار مستقيم ، فصنع زاوية  قياسها $\theta$ مع محور x  الموجب ، وقد مثل مقدار المتجه $\left|v\right|$ سرعة هذا الجسم. 

​​​​​​​

 تمثل V_x المركبة الأفقية للسرعة المتجهة ، ويمثل v_y المركبة  الرأسية لهذه السرعة حيث : 

يمكن استعمال النسب المثلثية لكتابة المركبتين الأفقية و الرأسية للسرعة المتجهة بدلالة الزاوية $\theta$ التي تصنعها السرعة المتجهة مع محور x  الموجب كما يأتي : 

$$\begin{gathered} {\mathit{v}}_{\mathbf{x}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{\left|}\mathbf{v}\mathbf{\right|}\mathbf{ }\mathit{c}\mathit{o}\mathit{s}\mathbf{ }\mathit{\theta } \\ {\mathit{v}}_{\mathbf{y}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{\left|}\mathbf{y}\mathbf{\right|}\mathbf{ }\mathbf{sin}\mathbf{ }\mathit{\theta } \end{gathered}$$

 

عندئذ ، يمكن كتابة السرعة المتجهة بالصورة الإحداثية كما يأتي  :

$\mathbf{ }\mathbf{v}\mathbf{=}\mathbf{ }\mathbf{<}\mathbf{ }\left|v\right|\mathbf{ }\mathbf{cos\theta }\mathbf{ }\mathbf{,}\mathbf{ }\left|v\right|\mathbf{ }\mathbf{sin\theta }\mathbf{>}$

 

مثال 

كرة قدم :​​​​​​​ ركل ريان كرة بسرعة 25m/s ، كما في الشكل المجاور ، وبزاوية مقدارها $40°$  مع الأفقي . أكتب المتجه الذي يمثل السرعة المتجهة للكرة بالصورة الإحداثية . 

---