حلول أسئلة كتاب الطالب وكتاب التمارين
أسئلة أتحقق من فهمي
أتحقق من فهمي صفحة 82
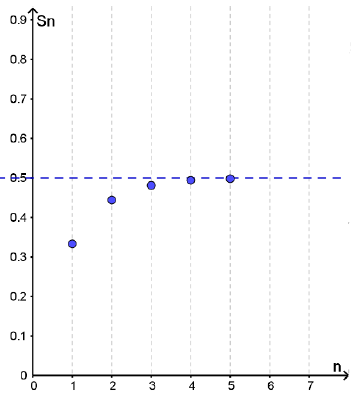
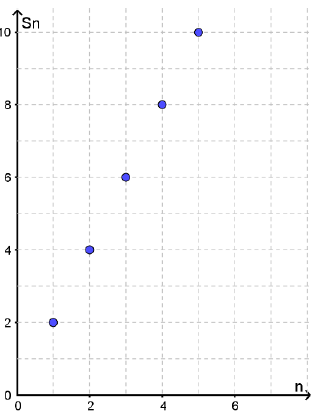
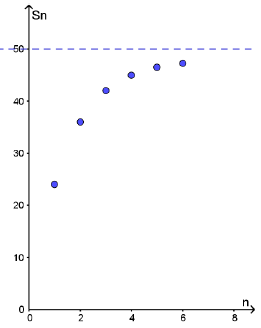
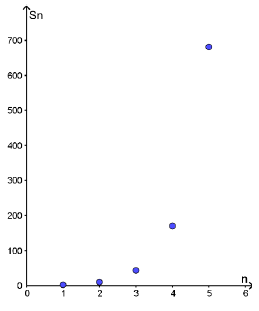
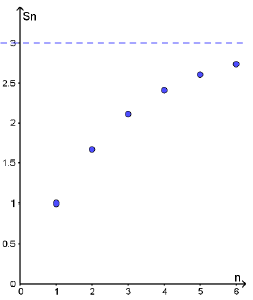
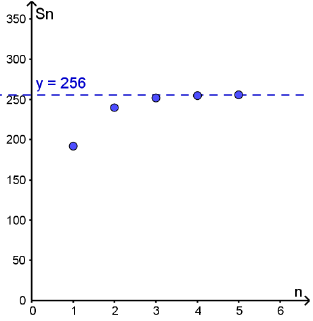
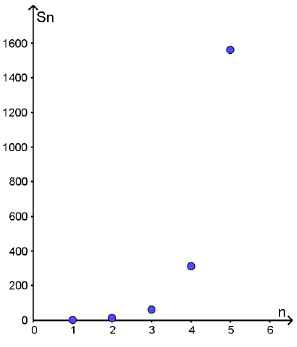
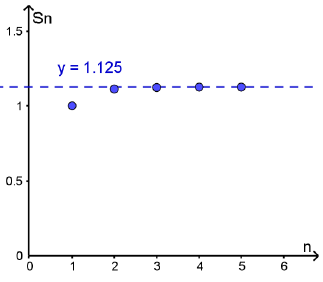
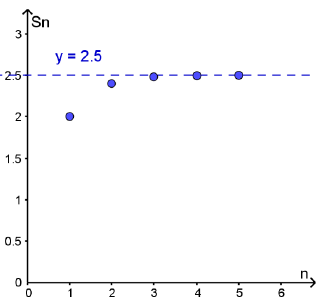
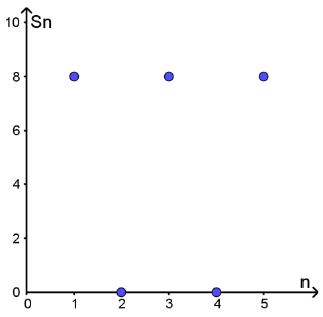
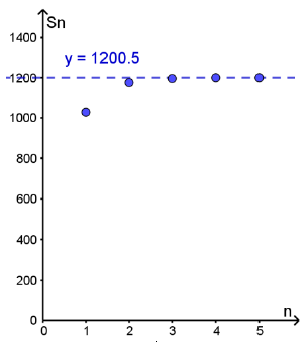
أجد المجاميع الجزئية للقيم : ، لكل متسلسلة هندسية لا نهائية ، ثم أمثلها بيانيًا :
الحل :
|
تمثيل الأزواج المرتبة :
|
|
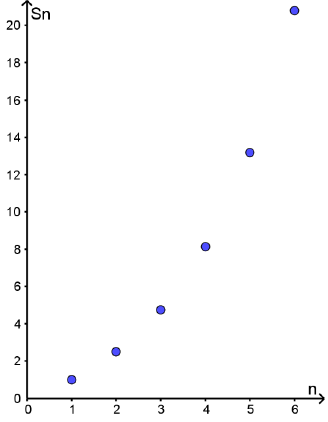
تمثيل الأزواج المرتبة :
|
أتحقق من فهمي صفحة 85
أُحدِّد إذا كانت المتسلسلات الهندسية اللانهائية الآتية متقاربة أم متباعدة، ثم أجد المجموع للمتقاربة منها :
الحل :
|
أجد قيمة الأساس r بقسمة الحد الثاني على الأول : بما أنّ ، فإن المتسلسلة متقاربة ويُمكن إيجاد مجموعها : صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
| أجد قيمة الأساس r بقسمة الحد الثاني على الأول : ، بما أن ، فإن المتسلسلة متباعدة ولا يمكن إيجاد مجموعها . | |
|
إيجاد الحد الأول بتعويض k = 1 في الحد العام للمتسلسلة : الأساس وبما أنّ ، فإن المتسلسلة متقاربة ويُمكن إيجاد مجموعها : صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
أتحقق من فهمي صفحة 86
أكتب العدد العشري الدوري في صورة كسر عادي.
الحل :
وهذا يُمثِّل متسلسلة لانهائية ، حدها الأول ، ويُمكِن إيجاد أساسها بقسمة الحد الثاني على الحد الأول
بما أنَّ 1 > 0.01 = | 0.01 | ، فإنَّ هذه المتسلسلة متقاربة، ويُمكِن إيجاد مجموعها على النحو الآتي:
صيغة مجموع المتسلسة الهندسية المتقاربة :
بتعويض
أتحقق من فهمي صفحة 87
أراجيح : دفع هُمام أرجوحة ابنته ، فلاحظ أنَّها قطعت مسافة 2 mبين أبعد نقطتين تصلهما ، ثم قطعت في كل مرَّة تالية % 95 من المسافة التي
قطعتها في المرَّة السابقة. أجد مجموع المسافات التي قطعتها الأرجوحة حتى توقَّفت عن الحركة.
الحل :
المسافات التي قطعتها الأرجوحة يساوي مجموع المتسلسلة : ، وهي متسلسلة هندسية أساسها r = 0.95 ، وهي متسلسلة هندسية متقاربة يمكن إيجاد مجموعها لأن
صيغة مجموع المتسلسة الهندسية المتقاربة :
أسئلة أتدرب وأحل المسائل
أجد المجاميع الجزئية لقيَم n الصحيحة ، حيث ، لكل من المتسلسلات الهندسية اللانهائية الآتية ، ثم أُمثّلها بيانيًّا :
الحل :
| الحد العام للمتسلسلة | |
|
بتمثيل الأزواج المرتبة :
|
|
| الحد العام للمتسلسلة | |
|
بتمثيل الأزواج المرتبة :
|
| الحد العام للمتسلسلة | |
|
تمثيل الأزواج المرتبة :
|
| الحد العام للمتسلسلة | |
|
تمثيل الأزواج المرتبة :
|
| الحد العام للمتسلسلة | |
|
تمثيل الأزواج المرتبة :
|
| الحد العام للمتسلسلة | |
|
تمثيل الأزواج المرتبة :
|
أُحدِّد إذا كانت المتسلسلات الهندسية اللانهائية الآتية متقاربة أم متباعدة، ثم أجد المجموع للمتقاربة منها :
الحل :
| أجد قيمة الأساس r بقسمة الحد الثاني على الأول : بما أنّ ، فإن المتسلسلة متقاربة
ويُمكن إيجاد مجموعها : صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
| أجد قيمة الأساس r بقسمة الحد الثاني على الأول : بما أنّ ، فإن المتسلسلة متباعدة ولا يمكن إيجاد مجموعها |
|
|
أجد قيمة الأساس r بقسمة الحد الثاني على الأول : بما أنّ ، فإن المتسلسلة متقاربة ويُمكن إيجاد مجموعها : صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
|
أجد قيمة الأساس r بقسمة الحد الثاني على الأول : بما أنّ ، فإن المتسلسلة متقاربة ويُمكن إيجاد مجموعها : صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
|
أجد قيمة الأساس r بقسمة الحد الثاني على الأول : بما أنّ ، فإن المتسلسلة متقاربة ويُمكن إيجاد مجموعها : صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
|
أجد قيمة الأساس r بقسمة الحد الثاني على الأول : بما أنّ ، فإن المتسلسلة متقاربة ويُمكن إيجاد مجموعها : صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
أكتب كُلًّا من الأعداد العشرية الدورية الآتية في صورة كسر عادي:
الحل :
|
متسلسلة هندسية متقاربة لأن أساسها r = 0.1 أقل من 1 تعويض في صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
متسلسلة هندسية متقاربة لأن أساسها r = 0.01 أقل من 1 تعويض في صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
متسلسلة هندسية متقاربة لأن أساسها r = 0.1 أقل من 1 تعويض في صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
متسلسلة هندسية متقاربة لأن أساسها r = 0.1 أقل من 1 تعويض في صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
متسلسلة هندسية متقاربة لأن أساسها r = 0.01 أقل من 1 تعويض في صيغة مجموع المتسلسة الهندسية المتقاربة : |
|
متسلسلة هندسية متقاربة لأن أساسها r = 0.1 أقل من 1 تعويض في صيغة مجموع المتسلسة الهندسية المتقاربة : |
كرات : سقطت كرة مطّاطية من ارتفاع 20 m رأسيًّا في اتجاه أرض أفقية . وعند اصطدامها بالأرض ارتدَّت إلى أعلى مسافة تُعادل ما نسبته % 70 من الارتفاع الذي
سقطت منه في المرَّة السابقة . بافتراض أنَّ الكرة سقطت رأسيًّا ثم ارتدَّت رأسيًّا عددًا لانهائيًّا من المرّات :
19) أجد الحد العام الذي يمثل المسافات التي قطعتها الكرة عندما ارتدت عن الأرض n مرة .
الحل :
المتسلسلة : ،
الحد العام :
20) أجد
الحل :
21) مراوح : تدور مروحة بسرعة مقدارها 12 دورة في الثانية الواحدة . وعند فصل التيار الكهربائي عنها تتباطأ سرعتها بما نسبته % 75 من دوراتها في كل ثانية لاحقة.
أجد عدد الدورات التي ستدورها المروحة قبل أنْ تتوقَّف عن الدوران بصورة كلية.
الحل :
المتسلسلة :
عدد الدورات = 48 دورة .
22) أحُلُّ المسألة الواردة في بند (مسألة اليوم).
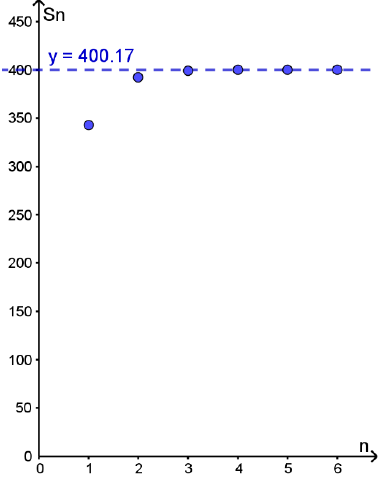
مسألة اليوم لدى ماجد شاحن كهربائي مُتنقِّل، يستمر في الشحن مدَّة 8 ساعات إذا كان مشحونًا شحنًا كاملاً. لاحظ ماجد أنَّ الشاحن أخذ يعمل بما نسبته % 98 من
عدد ساعات الشحن في اليوم السابق له بسبب عطل فيه. كيف يُمكِن تحديد مجموع ساعات عمل هذا الشاحن قبل تعطُّله بصورة كاملة؟
الحل :
عدد الساعات = 400 ساعة .
أسئلة مهارات التفكير العليا
23) أكتشف الخطأ : أوجد سفيان قيمة : على النحو الآتي :
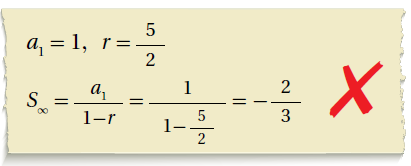
أكتشف الخطأ في حَلِّ سفيان، ثم أُصحِّحه.
الحل :
الخطأ في حل سفيان أنه لم يلاحظ أن ، لذا : المتسلسلة متباعدة ولا يمكن إيجاد مجموعها .
24) مسألة مفتوحة : أجد متسلسلة هندسية لانهائية مجموعها 6، مُبرِّرًا إجابتي.
الحل :
إجابة محتملة :
25) تحدٍّ : إذا كان الحد الأول لمتسلسلة هندسية لانهائية متقاربة هو a حيث a > 0 ، والحد الثالث فيها هو 4 ، فأجد جميع الاحتمالات المُمكِنة لمجموع المتسلسلة
بدلالة a .
الحل :
المتسلسلة هي :
الحد الثالث = 4 ، إذن :
وبحل المعادلة :
الاحتمالات الممكنة لمجموع المتسلسلة :
إما :
أو :
أسئلة كتاب التمارين
أجد المجاميع الجزئية لقِيَم n الصحيحة ، حيث : ، لكلٍّ من المتسلسلات الآتية، ثم أُمثِّلها بيانيًّا :
الحل :
|
تمثيل الأزواج المرتبة :
|
|
|
تمثيل الأزواج المرتبة :
|
|
|
تمثيل الأزواج المرتبة :
|
|
|
تمثيل الأزواج المرتبة :
|
|
|
تمثيل الأزواج المرتبة :
|
|
|
تمثيل الأزواج المرتبة :
|
|
أُحدِّد إذا كانت المتسلسلات الآتية متقاربة أم متباعدة، ثم أجد المجموع للمتقاربة منها :
الحل :
| متباعدة | |
| متقاربة |
|
| متقاربة |
|
| متقاربة |
|
| متقاربة |
|
| متباعدة |
أكتب كُلًّا من الأعداد العشرية الدورية الآتية في صورة كسر عادي :
الحل :
| 19) كراسي : حرَّك يوسف كرسيا هزازًا مرّة واحدة، وقد لاحظ أنّ قاعدة الكرسي المُقوَّسة مثَّلت مسافة 1.1 m أول مرَّة، ثم مثَّلت في كل مرَّة تالية ما نسبته % 68 من المسافة التي مثَّلتها في المرَّة التي سبقتها. أجد مجموع المسافات التي مثَّلتها قاعدة الكرسي الهزّاز في هذه الأثناء حتى توقَّف عن الحركة بصورة كاملة. |  |
الحل :