المثلثات متطابقة الضلعين والمثلثات متطابقة الأضلاع

 

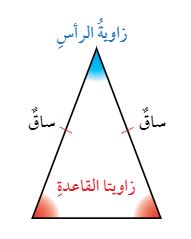
تعلمت سابقا أن المثلث المتطابق الضلعين هو المثلث الذي فيه ضلعان متطابقان على الأقل.

إن لأجزاء المثلث المتطابق الضلعين أسماء خاصة،

1- إذ يسمى الضلعان المتطابقان الساقين

2- وتسمى الزاوية التي ضلعاها الساقان زاوية الرأس

3- ويسمى الضلع الثالث القاعدة

4- والزاويتان المكونتان من القاعدة والضلعين المتطابقين تسميان زاويتي القاعدة

 

 

 

---

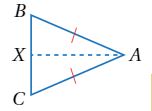
مثال 1 : في $∆ABC$  إذا علمت أن $\overline{AB} \cong \overline{AC}$ فأثبت أن $\angle B \cong \angle C$ باستعمال البرهان ذي العامودين 

 

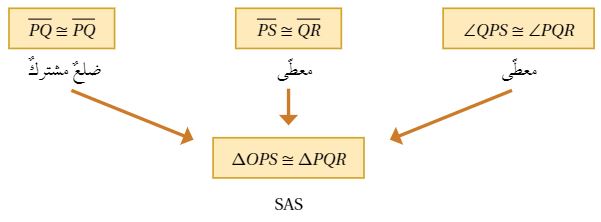
العبارات	المبررات
1- افرض أن X نقطة المنتصف $\overline{BC}$	1- كل قطعة مستقيمة لها نقطة منتصف واحدة
2- أرسم قطعة مساعدة $\overline{AX}$	2- كل نقطتين تحددان مستقيماً
3-$\overline{BX} \cong \overline{CX}$	3- X نقطة منتصف $\overline{BC}$
4-$\overline{AB} \cong \overline{AC}$	4- معطى
5-$\overline{AX}$	5- ضلع مشترك
6-$△ABX \cong ACX$	6- SSS
7-$\angle B \cong \angle C$	7- زاويتان متناظرتان في مثلثين متطابقين

 

 

 

---

أتعلم :

يمكنني استعمال نظريات المثلثات المتطابقة الضلعين في تحديد القطع المستقيمة  المتطابقة والزوايا المتطابقة في أشكال هندسية تحتوي مثلثات متطابقة الضلعين

 

 

 

---

مثال 2 : 

1- أسمي زاويتين متطابقتين غير مشار إلى تطابقهما في الشكل : 

  $\angle AFC \cong \angle ACF \mathrm{فإن} \mathrm{لذا} , \overline{AF} \mathrm{تقابل} \angle ACF و \overline{AC} \mathrm{تقابل} \angle AFC$

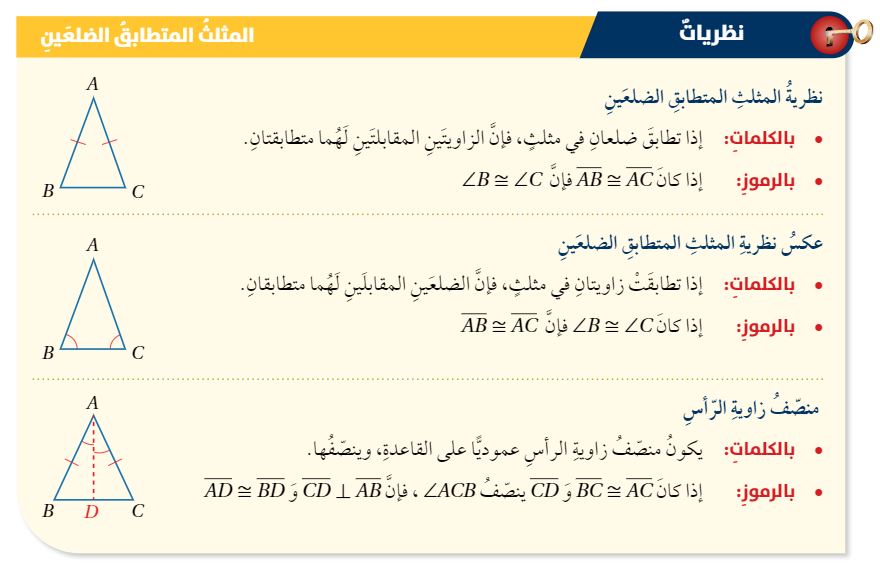
 ( نظرية المثلث المتطابق الضلعين )

 

 

 

2- أسمي قطعتين مستقيمتين متطابقتين غير مشار إلى تطابقهما في الشكل 

$\overline{BC} \cong \overline{BF} \mathrm{فإن} \mathrm{لذا} , \angle BCF \mathrm{تقابل} \overline{BF} و \angle BFC \mathrm{تقابل} \overline{BC}$

 ( عكس نظرية المثلث المتطابق الضلعين )

 

---

النتيجة هي نظرية يكون برهانها مبنيا على نظرية أخرى.

ويمكن استعمال النتيجة لتبرير خطوات البراهين، أو حل أسئلة ذات علاقة. وفي ما يأتي نتيجتان لنظرية المثلث المتطابق الضلعين، وعکس نظرية المثلث المتطابق الضلعين:

 

---

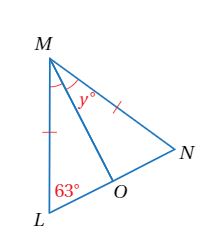
مثال 3 : 

1 - أجد قيمة  y  في الشكل المجاور  

بما أن $\angle NMO \cong \angle LMO$ إذن $\overline{MO}$ منصف لزاوية الرأس في مثلث متطابق الضلعين

وبذلك فإن $\overline{MO} \perp \overline{LN}$ ومنه  $m\angle MON = 90°$

وبما أن$△MLN$ متطابق الضليعن فإن $\angle L \cong \angle N$ ومنه فإن $m\angle N = 63°$

                                                                    $m\angle N + m\angle MON + Y = 180°$

                                                                              $63° + 90° + Y = 180°$

                                                                      $153°+ Y = 180°\Rightarrow Y = 27°$

 

إذن قيمة Y  تساوي $27°$

 

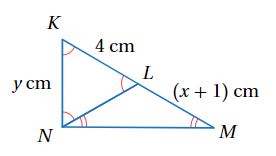
2- أجد قيمة كل من x و  y  في الشكل المجاور  

الخطوة 1 : أجد قيمة  y

بما أن $\angle KLN \cong \angle KNL \cong \angle LNK$ فإن $△KLN$ متطابق الأضلاع 

ومنه فإن $y = 4 cm$

 

.الخطوة 2 : أجد قيمة X

بما أن $\angle LMN \cong LNM$ فإن $\overline{LM} \cong \overline{LN}$ ومنه فإن $△LMN$ متطابق الضلعين

وبما أن $△KLN$ متطابق الأضلاع فإن $LN = 4$

                                    $LM=LN \Rightarrow 4=x+1\Rightarrow x=3$ 

إذن قيمة Y  تساوي $3 cm$

 

 

---

 

مثال 4 : 

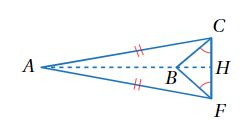
برج المنقذ : في برج المنقذ المجاور إذا علمت $\angle QPS \cong \angle PQR و \overline{PS} \cong \overline{QR}$ فأثبت أن : 

 

 

 

 

 

1- $∆QPS \cong ∆ PQR$

 

                                     

 

 

2-$∆QPT$ متطابق الضلعين 

 

العبارات	المبررات
1- $\angle PTS \cong \angle QTR$	1- زاويتان متقابلتان بالرأس
2-$\angle PSQ \cong \angle QRP$	2- زاويتان متناظرتان في مثلثين متطابقين
3- $\overline{PS} \cong \overline{QR}$	3-معطى
4- $△QTR \cong △PTS$	4-  AAS
5- $\overline{PT}\cong \overline{QT}$	5- ضلعان متناظران في مثلثين متطابقين
6- $△QPT$ متطابق الضلعين	6-تعريف المثلث المتطابق الضلعين