الرياضيات فصل ثاني

مسألة اليوم صفحة 31:

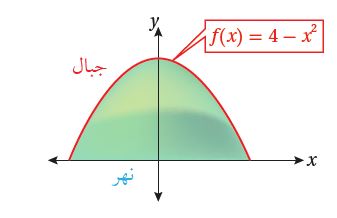
يمثل الجزء المظلل بالأخضر في الشكل الآتي حقول منطقة زراعية تحيط بها سلسلة من الجبال،

ويمثل منحنى الاقتران: $f\left(x\right) = 4-x^2$ الحد الفاصل بين سلسلة الجبال والمنطقة الزراعية،

ويمثل المحور $x$ حافة النهر الذي يطل على المنطقة الزراعية.

أجد المساحة الكلية للمنطقة الزراعية، علمًا بأن $x$ و $y$ مقيسان بالكيلومتر.

 

 

الحل:

أولًا:جد حدود التكامل، بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة: 

                                                                              $$\begin{gathered} 4-x^2 = 0 \\ \left(2-x\right)\left(2+x\right)=0 \\ (2-x)=0 or (2+x)=0 \\ \to x= 2 , x = -2 \end{gathered}$$      

إذن، حدود التكامل هي : $-2, 2$

 

ثانيًا:جد المساحة الكلية للمنطقة الزراعية باستخدام قانون التكامل

        (المنطقة تقع فوق المحور $x$ من الرسم):

                                                                                                                         $$\begin{gathered} {\int }_{-2}^2\left(4-x^2\right) dx = \left(4x - \frac{x^3}{3}\right) \overline{)\begin{array}{c} 2\\ -2\end{array} } \\ = \left(4\left(2\right) - \frac{2^3}{3}\right)-\left(4\left(-2\right) - \frac{{\left(-2\right)}^3}{3}\right) \\ =\left(8-\frac{8}{3}\right)-\left(-8 -\left(\frac{-8}{3}\right)\right) \\ =8-\frac{8}{3}+8-\frac{8}{3} \\ = 16-\frac{16}{3} \\ = \frac{48}{3} -\frac{16}{3} =\frac{32}{3} \end{gathered}$$

 

إذن، المساحة تقريبًا 10.67 كيلو متر مربع.

---

                                                                                     

أتحقق من فهمي صفحة 33:

أجد مساحة المنطقة المحصورة بين منحنى الاقتران:$f\left(x\right)=x+3$، والمحور $x$،

والمستقيمين : $x=-1$ ، و $x=3$ .

 

الحل:

الخطوة 1: جد الإحداثي $x$  لنقاط تقاطع منحنى الاقتران مع المحور $x$

                  بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                 $$\begin{gathered} x+3 = 0 \\ \to x=-3 \end{gathered}$$

 الإحداثي $x=-3$ لا يقع ضمن الفترة المعطاة $\left[-1 , 3\right]$ لذلك نهمله.

 

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور $x$

                  باختيار عدد يقع ضمن الفترة $\left[-1 , 3\right]$ وتعويضه بالاقتران، وليكن 0 :

                                        $$\begin{gathered} f\left(0\right)=0+3 \\ = 3>0 \end{gathered}$$

إذن منحنى الاقتران يقع فوق المحور  $x$ لأن نتيجة التعويض موجبة.

 

الخطوة 3: جد المساحة عن طريق التكامل

                  $$\begin{gathered} A = {\int }_{-1}^{ 3} (x+3) dx \\ = \left(\frac{x^2}{2}+3x\right) \overline{)\begin{array}{c} 3\\ -1\end{array}} \\ =(\frac{{\left(3\right)}^2}{2}+3\left(3\right))-(\frac{{(-1)}^2}{2}+3(-1)) \\ =\left(\frac{9}{2}+9\right)-(\frac{1}{2}-3) \\ =(\frac{9}{2}+\frac{18}{2})-(\frac{1}{2}-\frac{6}{2}) \\ =\frac{27}{2}-\left(-\frac{5}{2}\right)=\frac{32}{2}=16 \end{gathered}$$

إذن، المساحة هي : 16 وحدة مربعة.

 

---

أتحقق من فهمي صفحة 34:

أجد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right) = x^2-4$، والمحور $x$ ،

والمستقيمين: $x=-1$ ، و $x=1$ .

الحل:

الخطوة 1: جد الإحداثي $x$ لنقاط تقاطع منحنى الاقتران مع المحور $x$

                                     بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                                      $$\begin{gathered} x^2 - 4 = 0 \\ (x-2)(x+2)=0 \\ (x-2)=0 or (x+2)=0 \\ x = 2 or x = -2 \end{gathered}$$

إذن الإحداثي $x=2 , x=-2$ لا يقع ضمن الفترة المعطاة $\left[-1 , 1\right]$ لذلك نهمله.

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور $x$

                   باختيار عدد يقع ضمن الفترة $[-1 , 1]$ وتعويضه بالاقتران، وليكن 0 :

                                          $$\begin{gathered} f\left(0\right) =0^2-4 \\ = -4 <0 \end{gathered}$$

إذن منحنى الاقتران يقع تحت المحور $x$ لأن نتيجة التعويض سالبة.

 

 

الخطوة 3: جد المساحة عن طريق التكامل

                   $$\begin{gathered} A =- {\int }_{-1}^{ 1} (x^2-4) dx \\ =-(\frac{x^3}{3}-4x) \overline{)\begin{array}{c} 1\\ -1\end{array}} \\ =- (\left(\frac{{\left(1\right)}^3}{3}-4\left(1\right)\right)-\left(\frac{{\left(-1\right)}^3}{3}-4\left(-1\right)\right)) \\ =- (\left(\frac{1}{3}-4\right)-\left(\frac{-1}{3}+4\right)) \\ =-(\frac{1}{3}-4+\frac{1}{3}-4) \\ =-(\frac{2}{3}-8) \\ =-\frac{2}{3}+\frac{24}{3} \\ =\frac{22}{3} \end{gathered}$$

إذن، المساحة هي : $\frac{22}{3}$ وحدة مربعة.

---

 

أتحقق من فهمي صفحة 36:

جد مساحة المنطقة المحصورة بين منحنى الاقتران:$f\left(x\right)=x^2+2x$، والمحور $x$ ،

والمستقيمين: $x=-1$, ,   $x=-3$.

 

الحل:

الخطوة 1: جد الإحداثي $x$  لنقاط تقاطع منحنى الاقتران مع المحور $x$

                                        بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                                         $$\begin{gathered} x^2+2x = 0 \\ x(x+2)=0 \\ x=0 or x+2 = 0 \\ x=0 or x=-2 \end{gathered}$$

إذن الإحداثي $x=0$ لا يقع ضمن الفترة المعطاة $\left[-3 , -1\right]$ لذلك نهمله.

ولكن العدد $-2$ يقع ضمن الفترة$[-3 , -1]$ ، لذلك نقسم الفترة إلى فترتين هما:

$[-3 , -2] , [-2 , -1]$

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور $x$

                   باختيار عدد يقع ضمن الفترة $[-3 , -2]$ وتعويضه بالاقتران، وليكن $\left(-\frac{5}{2}\right)$ :

                                          $$\begin{gathered} f(-\frac{5}{2})={(-\frac{5}{2})}^2+2(-\frac{5}{2}) \\ = \frac{25}{4}-5 \\ = \frac{25}{4}-\frac{20}{4} \\ = \frac{5}{4} >0 \end{gathered}$$

بما أن ناتج التعويض موجب ، فإن منحنى الاقتران يقع فوق المحور $x$ في الفترة $[-3 , -2]$

 

وباختيار عدد يقع ضمن الفترة $[-2 , -1]$ وتعويضه بالاقتران، وليكن $\left(-\frac{3}{2}\right)$:

                              $$\begin{gathered} f(-\frac{3}{2})={(-\frac{3}{2})}^2+2(-\frac{3}{2}) \\ = \frac{9}{4}-3 \\ = \frac{9}{4}-\frac{12}{4} \\ = -\frac{3}{4} <0 \end{gathered}$$

بما أن ناتج التعويض سالب ، فإن منحنى الاقتران يقع تحت المحور $x$ في الفترة $[-2 , -1]$ .

 

 

الخطوة 3: جد المساحة عن طريق التكامل:

                   $$\begin{gathered} A = {\int }_{-3}^{-2} (x^2+2x) dx - {\int }_{-2}^{-1} (x^2+2x) dx \\ =(\frac{x^3}{3}+\frac{2x^2}{2}) \overline{)\begin{array}{c}-2\\ -3\end{array}} - (\frac{x^3}{3}+\frac{2x^2}{2}) \overline{)\begin{array}{c}-1\\ -2\end{array}} \\ =(\frac{x^3}{3}+x^2) \overline{)\begin{array}{c}-2\\ -3\end{array}} - (\frac{x^3}{3}+x^2) \overline{)\begin{array}{c}-1\\ -2\end{array}} \\ =\left((\frac{{\left(-2\right)}^3}{3}+{\left(-2\right)}^2)-(\frac{{\left(-3\right)}^3}{3}+{\left(-3\right)}^2)\right) - \left((\frac{{\left(-1\right)}^3}{3}+{\left(-1\right)}^2)-(\frac{{\left(-2\right)}^3}{3}+{(-2)}^2)\right) \\ = \left((\frac{\left(-8\right)}{3}+4)-(\frac{\left(-27\right)}{3}+9)\right) - \left((\frac{\left(-1\right)}{3}+1)-(\frac{-8}{3}+4)\right) \\ =\left(\left(\frac{-8}{3}+4\right)-\left(-9+9\right))\right) - \left(-\frac{1}{3}+1+\frac{8}{3}-4)\right) \\ = -\frac{8}{3}+4 -\left(\frac{7}{3}-3\right) \\ =-\frac{8}{3}+4 -\frac{7}{3}+3 \\ =-\frac{15}{3}+7 \\ = -5+7 \\ =2 \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

إذن، المساحة هي :2 وحدة مربعة.

---

 

أتحقق من فهمي صفحة 38:

a) أجد مساحة المنطقة المحصورة بين منحنى الاقتران $f\left(x\right) = x^2 +5x + 4$  ، والمحور $x$

 

 

الحل:

الخطوة 1: جد الإحداثي $x$ لنقاط تقاطع منحنى الاقتران مع المحور $x$

                 بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                 $$\begin{gathered} x^2 +5x + 4=0 \\ \left(x+4\right)\left(x+1\right)=0 \\ (x+4)=0 or (x+1)=0 \\ \to x=-4 or x=-1 \end{gathered}$$

هذه الإحداثيات تمثل حدود التكامل.

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور $x$

                  باختيار عدد يقع ضمن الفترة $\left[-4 , -1\right]$ وتعويضه بالاقتران، وليكن$\left(-2\right)$:

                  $$\begin{gathered} f(-2) ={\left( -2\right)}^2 +5\left(-2\right) + 4 \\ = 4 -10 +4 \\ = -2 <0 \end{gathered}$$

بما أن ناتج التعويض سالب ، فإن منحنى الاقتران يقع تحت المحور $x$ في الفترة $[-4 , -1]$

 

الخطوة 3: جد المساحة عن طريق التكامل:

                                           $$\begin{gathered} A =- {\int }_{-4}^{-1} (x^2+5x+4) dx \\ =-(\frac{x^3}{3}+\frac{5x^2}{2}+4x) \overline{)\begin{array}{c}-1\\ -4\end{array}} \\ =- ((\frac{{\left(-1\right)}^3}{3}+\frac{5{\left(-1\right)}^2}{2}+4\left(-1\right))-(\frac{{\left(-4\right)}^3}{3}+\frac{5{(-4)}^2}{2}+4\left(-4\right))) \\ =- ((\frac{-1}{3}+\frac{5}{2}-4)-(\frac{-64}{3}+\frac{80}{2}-16)) \\ =-(-\frac{1}{3}+\frac{5}{2}-4+\frac{64}{3}-40+16) \\ =-(\frac{63}{3}+\frac{5}{2}-28) \\ =-(21+2.5-28) \\ =-\left(-4.5\right)=4.5 \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

إذن، المساحة هي :4.5 وحدة مربعة.

---

 

b) أجد مساحة المنطقة المحصورة بين منحنى الاقتران $f\left(x\right) = x^3 - 9x$  ، والمحور $x$

 

الحل:

الخطوة 1: جد الإحداثي $x$ لنقاط تقاطع منحنى الاقتران مع المحور $x$

                   بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                                           $$\begin{gathered} x^3 - 9x = 0 \\ x(x^2-9)=0 \\ x\left(x-3\right)\left(x+3\right)=0 \\ \to x=0 , x=3 , x=-3 \end{gathered}$$

هذه الإحداثيات تمثل حدود التكامل.

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور $x$

                  باختيار عدد يقع ضمن الفترة $\left[-3 , 0\right]$ ، وليكن $-1$ وتعويضه بالاقتران:

                  $$\begin{gathered} f(-1) ={( -1)}^3 - 9(-1) \\ =-1+9 \\ =8 >0 \end{gathered}$$

                                     بما أن ناتج التعويض موجب ، فإن منحنى الاقتران يقع فوق المحور $x$ بالفترة $[-3 , 0]$

 

               وباختيار عدد يقع ضمن الفترة $\left[0 , 3\right]$، وليكن $1$وتعويضه بالاقتران:

               $$\begin{gathered} f\left(1\right) ={( 1)}^3 - 9\left(1\right) \\ =1-9 \\ =-8 <0 \end{gathered}$$

             بما أن ناتج التعويض سالب ، فإن منحنى الاقتران يقع تحت المحور $x$ بالفترة $[0 , 3]$

 

الخطوة 3: جد المساحة عن طريق التكامل:

                                       

                  $$\begin{gathered} A = {\int }_{-3}^0 (x^3-9x) dx - {\int }_0^3 (x^3-9x) dx \\ =(\frac{x4}{4}-\frac{9x^2}{2}) \overline{)\begin{array}{c} 0\\ -3\end{array}} - (\frac{x4}{4}-\frac{9x^2}{2}) \overline{)\begin{array}{c}3\\ 0\end{array}} \\ =\left((\frac{\left(0\right)4}{4}-\frac{9{\left(0\right)}^2}{2})-(\frac{{\left(-3\right)}^4}{4}-\frac{9{\left(-3\right)}^2}{2})\right) - \left((\frac{{\left(3\right)}^4}{4}-\frac{9{\left(3\right)}^2}{2})-(\frac{{\left(0\right)}^4}{4}-\frac{9{\left(0\right)}^2}{2})\right) \\ = \left(-(\frac{}{4}-\frac{81}{2})\right) - (\frac{}{4}-\frac{81}{2}) \\ =-\frac{81}{4}+\frac{81}{2}-\frac{81}{4}+\frac{81}{2} \\ = -\frac{162}{4}+\frac{162}{2} \\ =-\frac{162}{4}+\frac{324}{4} \\ =\frac{ 162}{4}=\frac{81}{2}=40.5 \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

إذن، المساحة هي :40.5 وحدة مربعة

 

---

 

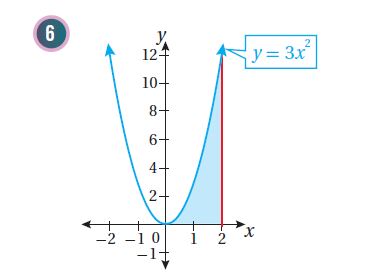
أتدرب وأحل المسائل صفحة 29:

 

أجد مساحة المنطقة المظللة في كل من التمثيلات البيانية الآتية:

 

 

                                                                                                            $$\begin{gathered} A={\int }_{-2}^1 (x^2+2) dx \\ = \left(\frac{x^3}{3}+2x\right) \overline{)\begin{array}{c} 1\\ -2\end{array} } \\ = \left(\frac{1^3}{3}+2\left(1\right)\right)- \left(\frac{{\left(-2\right)}^3}{3}+2\left(-2\right)\right) \\ = \left(\frac{1}{3}+2\right)- \left(\frac{-8}{3}-4\right) \\ = \left(\frac{1}{3}+\frac{6}{3}\right)- \left(\frac{-8}{3}-\frac{12}{3}\right) \\ = \frac{7}{3}-\left(\frac{-20}{3}\right) \\ = \frac{7}{3}+\frac{20}{3}=\frac{27}{3}=9 \end{gathered}$$

 

---

 

                                         

 

                                                                                                                                                                  $$\begin{gathered} A={\int }_4^9 \left(x^{\frac{3}{2}}\right) dx \\ = \left(\frac{x^{{\displaystyle \frac{5}{2}}}}{{\displaystyle \frac{5}{2}}}\right) \overline{)\begin{array}{c}9\\ 4\end{array} } \\ = \left(\frac{2}{5}\sqrt{x^5}\right)\overline{)\begin{array}{c}9\\ 4\end{array} } \\ =\frac{2}{5} \left(\sqrt{9^5} - \sqrt{4^5}\right) \\ = \frac{2}{5}(3^5 - 2^5) \\ = \frac{2}{5}(243 - 32) \\ = \frac{2}{5}\left(211\right)=\frac{422}{5} \end{gathered}$$

---

                                                                                                                                      $$\begin{gathered} A=-{\int }_2^4 \left(\frac{2}{x^2}-3\right) dx \\ =-{\int }_2^4 \left(2 x^{-2}-3\right) dx \\ =-(\frac{2x^{-1}}{-1}-3x) \overline{)\begin{array}{c}4\\ 2\end{array} } \\ =- (-\frac{2}{x}-3x)\overline{)\begin{array}{c}4\\ 2\end{array} } \\ = (\frac{2}{x}+3x)\overline{)\begin{array}{c}4\\ 2\end{array} } \\ = (\frac{2}{4}+3\left(4\right)) - (\frac{2}{2}+3\left(2\right)) \\ = (0.5+12) - (1+6) \\ = 12.5 -7 \\ = 5.5 \end{gathered}$$

---

 

                   

                 $$\begin{gathered} A = {\int }_{-1}^0 (x^3-3x) dx - {\int }_0^1 (x^3-3x) dx \\ =(\frac{x^4}{4}-\frac{3x^2}{2}) \overline{)\begin{array}{c} 0\\ -1\end{array}} - (\frac{x^4}{4}-\frac{3x^2}{2}) \overline{)\begin{array}{c}1\\ 0\end{array}} \\ =\left((\frac{{\left(0\right)}^4}{4}-\frac{3{\left(0\right)}^2}{2})-(\frac{{\left(-1\right)}^4}{4}-\frac{3{(-1)}^2}{2})\right) - \left((\frac{{\left(1\right)}^4}{4}-\frac{3{\left(1\right)}^2}{2})-(\frac{{\left(0\right)}^4}{4}-\frac{3{\left(0\right)}^2}{2})\right) \\ = \left(-(\frac{1}{4}-\frac{3}{2})\right) - (\frac{1}{4}-\frac{3}{2}) \\ =-\frac{1}{4}+\frac{3}{2}-\frac{1}{4}+\frac{3}{2} \\ = -\frac{2}{4}+\frac{6}{2} \\ =-\frac{1}{2}+\frac{6}{2} \\ =\frac{5}{2}=2.5 \end{gathered}$$

---

    

 

 

                                                                                                                                                   $$\begin{gathered} A={\int }_0^3 (x+1) dx \\ = (\frac{x^2}{2}+x) \overline{)\begin{array}{c} 3\\ 0\end{array} } \\ = (\frac{3^2}{2}+3)- (\frac{{\left(0\right)}^2}{2}+0) \\ = (\frac{9}{2}+3)- 0 \\ = 4.5+3 \\ = 7.5 \end{gathered}$$

---

 

                                                                $$\begin{gathered} A={\int }_0^2 \left(3x^2\right) dx \\ = \left(\frac{3x^3}{3}\right) \overline{)\begin{array}{c} 2\\ 0\end{array} }=\left(x^3\right) \overline{)\begin{array}{c} 2\\ 0\end{array} } \\ = 2^3 - 0^3 \\ = 8-0 \\ = 8 \end{gathered}$$                                                                        

---

 

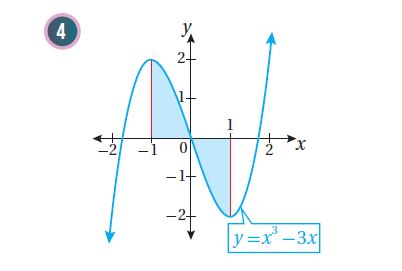
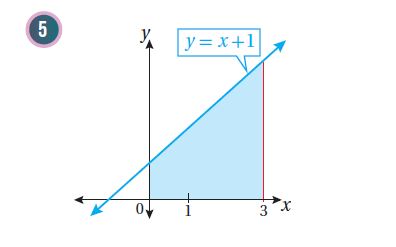
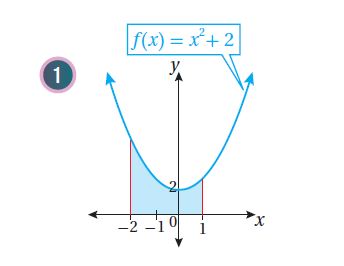
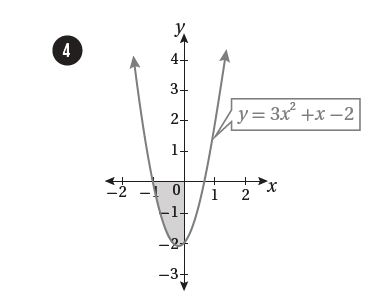
7)أجد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right) = 3x^2 -2x +2$، والمحور $x$ ،

   والمستقيمين: $x=0$، و $x=2$

 

الحل:

الخطوة 1: جد الإحداثي $x$  لنقاط تقاطع منحنى الاقتران مع المحور $x$

                  بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

 

                  $3x^2 -2x +2=0$

                 وبحساب المميز للمعادلة التربيعية:

                 $$\begin{gathered} ∆=b^2-4ac \\ = {\left(-2\right)}^2- 4\left(3\right)\left(2\right) \\ = 4-24 \\ = -20 \end{gathered}$$

 

            بما أن المميز سالب، فلا يوجد حل لهذه المعادلة،

            حدود التكامل هي: $2 , 0$

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور

                  باختيار عدد يقع ضمن الفترة $\left[0 , 2\right]$ ، وليكن 1 ونعوضه في قاعدة الاقتران:

                  $$\begin{gathered} f\left(1\right) = 3{\left(1\right)}^2 -2\left(1\right) +2 \\ = 3 -2+2 \\ =3 >0 \end{gathered}$$

                                   بما أن ناتج التعويض موجب ، فإن منحنى الاقتران يقع فوق المحور $x$ في الفترة $[0 , 2]$

 

 

الخطوة 3: جد المساحة عن طريق التكامل:

                   $$\begin{gathered} A={\int }_0^2 (3x^2-2x+2) dx \\ = (\frac{3x^3}{3}-\frac{2x^2}{2}+2x) \overline{)\begin{array}{c} 2\\ 0\end{array} }=(x^3-x^2+2x) \overline{)\begin{array}{c} 2\\ 0\end{array} } \\ = (2^3-2^2+2\left(2\right))-(0^3-0^2+2\left(0\right)) \\ = 8 - 4+4 \\ = 8 \end{gathered}$$

إذن المساحة هي: 8 وحدات مربعة.

---

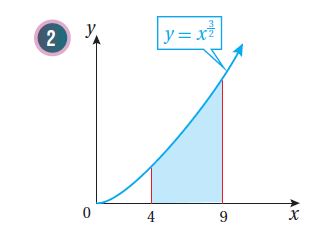
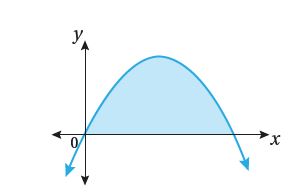
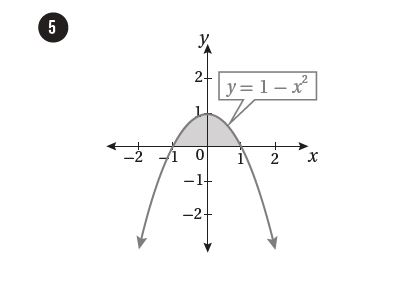
8)أجد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right) = 9-x^2$، والمحور $x$.

الحل:

الخطوة 1: جد الإحداثي $x$  لنقاط تقاطع منحنى الاقتران مع المحور $x$

                  بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                 

                $$\begin{gathered} 9-x^2 =0 \\ \left(3-x\right)\left(3+x\right)=0 \\ \left(3-x\right)=0 or \left(3+x\right)=0 \\ \to x=3 , x=-3 \end{gathered}$$

             هذه الإحداثيات تمثل حدود التكامل.

 

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور

                  باختيار عدد يقع ضمن الفترة $\left[-3, 3\right]$ وليكن 0 ونعوضه في قاعدة الاقتران:

                                    $$\begin{gathered} f\left(0\right) = 9-{\left(0\right)}^2 \\ = 9 > 0 \end{gathered}$$

 

    بما أن ناتج التعويض موجب ، فإن منحنى الاقتران يقع فوق المحور $x$ في الفترة $[-3, 3]$

 

الخطوة 3: جد المساحة عن طريق التكامل:

                  $$\begin{gathered} A={\int }_{-3}^3 (9-x^2) dx \\ = (9x - \frac{x^3}{3}) \overline{)\begin{array}{c} 3\\ -3\end{array} } \\ = (9\left(3\right) - \frac{{\left(3\right)}^3}{3})- (9\left(-3\right) - \frac{{\left(-3\right)}^3}{3}) \\ = (27-9)-(-27+9) \\ = 18 - \left(-18\right) \\ = 18 + 18 \\ = 36 \end{gathered}$$

 

إذن المساحة هي: 36 وحدة مربعة.

 

---

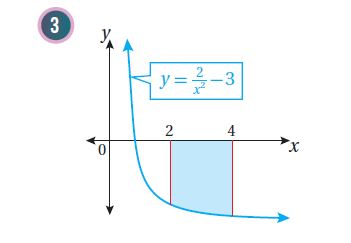
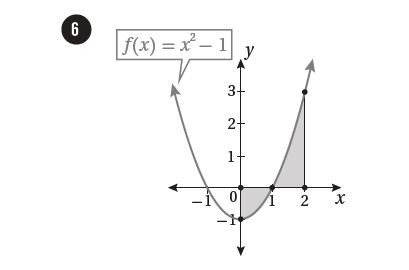
9)أجد مساحة المنطقة المحصورة بين منحنى الاقتران:$f\left(x\right) = x^3 +4x$، والمحور $x$ ،

    والمستقيمين: $x=-1$ ، و $x=2$

الحل:

الخطوة 1: جد الإحداثي $x$  لنقاط تقاطع منحنى الاقتران مع المحور $x$

                  بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                  $$\begin{gathered} x^3 +4x=0 \\ x(x^2+4)=0 \\ x= 0 \end{gathered}$$

                مميز العبارة $\left(x^2+4\right)$سالب ، لذلك لا أصفار لها .

                وحدود التكامل هي $-1, 2$

 

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور باختيار عدد:

                  1) يقع ضمن الفترة $\left[-1 , 0\right]$ ، وليكن $\left(-\frac{1}{2}\right)$ ونعوضه في قاعدة الاقتران: 

                      $$\begin{gathered} f(-\frac{1}{2}) = {\left(-\frac{1}{2}\right)}^3 +4\left(-\frac{1}{2}\right) \\ =-\frac{1}{8} - 2 \\ = -\frac{17}{8}< 0 \end{gathered}$$

 

                             بما أن ناتج التعويض سالب ، فإن منحنى الاقتران يقع تحت المحور $x$ في الفترة $[-1 , 0]$

 

            2) يقع ضمن الفترة $\left[0 , 2\right]$ ، وليكن $\left(1\right)$ ونعوضه في قاعدة الاقتران: 

                 $$\begin{gathered} f\left(1\right) = {\left(1\right)}^3 +4\left(1\right) \\ =1 + 4 \\ = 5> 0 \end{gathered}$$

                  بما أن ناتج التعويض موجب ، فإن منحنى الاقتران يقع فوق المحور $x$ في الفترة $[0 , 2]$

 

 

الخطوة 3: جد المساحة عن طريق التكامل:

                   $$\begin{gathered} A =- {\int }_{-1}^0 (x^3+4x) dx + {\int }_0^2 (x^3+4x) dx \\ =-(\frac{x^4}{4}+\frac{4x^2}{2}) \overline{)\begin{array}{c} 0\\ -1\end{array}} + (\frac{x^4}{4}+\frac{4x^2}{2}) \overline{)\begin{array}{c}2\\ 0\end{array} } \\ =(-\frac{x^4}{4}-2 x^2) \overline{)\begin{array}{c} 0\\ -1\end{array}} + (\frac{x^4}{4}+2 x^2) \overline{)\begin{array}{c}2\\ 0\end{array}} \\ =\left((-\frac{{\left(0\right)}^4}{4}-2 {\left(0\right)}^2)-(-\frac{{\left(-1\right)}^4}{4}-{2(-1)}^2)\right) + \left((\frac{{\left(2\right)}^4}{4}+2{\left(2\right)}^2)-(\frac{{\left(0\right)}^4}{4}+2 {\left(0\right)}^2)\right) \\ = \left(-(-\frac{1}{4}-2)\right) + (\frac{16}{4}+8) \\ =\frac{1}{4}+2+4+8 \\ = \frac{1}{4}+14 \\ =14\frac{1}{4} \\ =14.25 \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

إذن المساحة هي: 14.25 وحدات مربعة.

---

10)أجد مساحة المنطقة المحصورة بين منحنى الاقتران:$f\left(x\right) =-7+2x- x^2$، والمحور $x$،

    والمستقيمين: $x=4 , x=1$.

 

الحل:

الخطوة 1: جد الإحداثي $x$  لنقاط تقاطع منحنى الاقتران مع المحور $x$

                  بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

 

                                          $-7+2x- x^2 =0$

 

                                     وبحساب المميز للمعادلة التربيعية:

                                   $$\begin{gathered} ∆=b^2-4ac \\ = {\left(2\right)}^2- 4(-1)(-7) \\ = 4-28 \\ = -24 \end{gathered}$$

                              

             بما أن المميز سالب، فلا يوجد حل لهذه المعادلة،

             حدود التكامل هي: $1 , 4$

 

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور

                  باختيار عدد يقع ضمن الفترة $[1 , 4]$ وليكن $\left(2\right)$ ونعوضه في قاعدة الاقتران: 

                  $$\begin{gathered} f\left(2\right) =-7+2\left(2\right)- {\left(2\right)}^2 \\ = -7 + 4 -4 \\ = -7 <0 \end{gathered}$$

 

                              بما أن ناتج التعويض سالب ، فإن منحنى الاقتران يقع تحت المحور $x$ في الفترة $[1 , 4]$

 

الخطوة 3: جد المساحة عن طريق التكامل:

                   $$\begin{gathered} A=-{\int }_1^4 (-7+2x-x^2) dx \\ =-(-7x +\frac{2x^2}{2}-\frac{x^3}{3}) \overline{)\begin{array}{c}4\\ 1\end{array} } \\ = (7x -x^2 + \frac{x^3}{3})\overline{)\begin{array}{c}4\\ 1\end{array} } \\ = (7\left(4\right) -{\left(4\right)}^2 + \frac{{\left(4\right)}^3}{3}) - \left(7\right(1) -{\left(1\right)}^2 + \frac{{\left(1\right)}^3}{3}) \\ = (28-16+\frac{64}{3}) - (7-1+\frac{1}{3}) \\ = 12 +\frac{64}{3}-6-\frac{1}{3} \\ = 6 +\frac{63}{3} \\ = 6 +21 \\ = 27 \end{gathered}$$

 

إذن المساحة هي: 27 وحدات مربعة.

 

---

11)أجد مساحة المنطقة المحصورة بين منحنى الاقتران:$f\left(x\right) =5-x$ ، والمحور $x$ ،

    والمستقيمين:$x=5 , x=3$

الحل:

الخطوة 1: جد الإحداثي $x$  لنقاط تقاطع منحنى الاقتران مع المحور $x$

                  بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                  $$\begin{gathered} 5-x=0 \\ \to x=5 \end{gathered}$$

                   إذن تمثل الإحداثيات $3 , 5$ حدود التكامل.

 

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور

                  باختيار عدد يقع ضمن الفترة $\left[3 , 5\right]$ وليكن $\left(2\right)$ونعوضه في قاعدة الاقتران: 

                                         $$\begin{gathered} f\left(2\right) =5-2 \\ =3 > 0 \end{gathered}$$

 

                                        بما أن ناتج التعويض موجب ، فإن منحنى الاقتران يقع فوق المحور $x$ في الفترة $\left[3 ,5\right]$

 

 

الخطوة 3: جد المساحة عن طريق التكامل:

                  $$\begin{gathered} A={\int }_3^5 (5-x) dx \\ =(5x -\frac{x^2}{2}) \overline{)\begin{array}{c}5\\ 3\end{array} } \\ = (5\left(5\right) -\frac{{\left(5\right)}^2}{2}) - (5\left(3\right) -\frac{{\left(3\right)}^2}{2}) \\ = (25-\frac{25}{2}) - (15-\frac{9}{2}) \\ = 25 -\frac{25}{2}-15+\frac{9}{2} \\ = 10 -\frac{16}{2} \\ = 10-8 \\ = 2 \end{gathered}$$

 

 

إذن المساحة هي: 2 وحدة مربعة.

---

12)أجد مساحة المنطقة المحصورة بين منحنى الاقتران:$f\left(x\right) =\left(x+1\right)\left(x-4\right)$ ، والمحور $x$

الحل:

الخطوة 1: جد الإحداثي $x$  لنقاط تقاطع منحنى الاقتران مع المحور $x$

                  بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                   $$\begin{gathered} (x+1)(x-4)=0 \\ \left(x+1\right)=0 or \left(x-4\right)=0 \\ \to x = -1 , x=4 \end{gathered}$$

                   إذن تمثل الإحداثيات $-1 , 4$  حدود التكامل.

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور $x$

                  باختيار عدد يقع ضمن الفترة $\left[-1 , 4\right]$ وليكن $\left(0\right)$ ونعوضه في قاعدة الاقتران: 

                                          $$\begin{gathered} f\left(0\right) =(0+1)(0-4) \\ = \left(1\right)\left(-4\right) \\ = -4 < 0 \end{gathered}$$

 

                        بما أن ناتج التعويض سالب ، فإن منحنى الاقتران يقع تحت المحور $x$ في الفترة $[-1 , 4]$

 

الخطوة 3: جد المساحة عن طريق التكامل:

                   $$\begin{gathered} A=-{\int }_{-1}^4\left(x+1\right)\left(x-4\right) dx \\ =-{\int }_{-1}^4\left(x^2-4x + x -4\right) dx \\ =-{\int }_{-1}^4\left(x^2-3x -4\right) dx \\ =-(\frac{x^3}{3}-\frac{3x^2}{2}-4x) \overline{)\begin{array}{c} 4\\ -1\end{array} } \\ = (-\frac{x^3}{3}+\frac{3x^2}{2}+4x)\overline{)\begin{array}{c} 4\\ -1\end{array} } \\ = (-\frac{{\left(4\right)}^3}{3}+\frac{3{\left(4\right)}^2}{2}+4\left(4\right)) - (-\frac{{\left(-1\right)}^3}{3}+\frac{3{\left(-1\right)}^2}{2}+4\left(-1\right)) \\ = (-\frac{64}{3}+24+16) - (\frac{1}{3}+\frac{3}{2}-4) \\ = -\frac{64}{3}+40-\frac{1}{3}-\frac{3}{2}+4 \\ = -\frac{65}{3}-\frac{3}{2}+44 \\ = -\frac{ 130}{6}-\frac{9}{6}+\frac{ 264}{6} \\ = \frac{ 125}{6} \end{gathered}$$

 

إذن المساحة هي: $\left(\frac{125}{6}\right)$ وحدة مربعة.

 

---

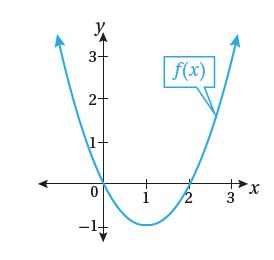
يبين الشكل الآتي منحنى الاقتران: $f\left(x\right) = x^2 -2x$ :

 

13)أجد مساحة المنطقة المحصورة بين منحنى الاقتران ، والمحور $x$ .

 

          الحل:

         يبين الشكل أن منحنى الاقتران يقع تحت المحور $x$ في الفترة $\left[0 , 2\right]$

    $$\begin{gathered} A=-{\int }_0^2(x^2-2x) dx \\ =-(\frac{x^3}{3}-\frac{2x^2}{2}) \overline{)\begin{array}{c}2\\ 0\end{array} } \\ = (-\frac{x^3}{3}+x^2)\overline{)\begin{array}{c}2\\ 0\end{array} } \\ = (-\frac{{\left(2\right)}^3}{3}+{\left(2\right)}^2) - (-\frac{{\left(0\right)}^3}{3}+{\left(0\right)}^2) \\ = (-\frac{8}{3}+4) - 0 \\ = -\frac{8}{3}+\frac{12}{3} \\ = \frac{ 4}{3} \end{gathered}$$

   إذن المساحة هي:$\left(\frac{4}{3}\right)$ وحدة مربعة.

 

 

14)أجد مساحة المنطقة المحصورة بين منحنى الاقتران، والمحور $x$ ، والمستقيم $x=3$ .

 

               الحل:

             يبين الشكل أن منحنى الاقتران يقع فوق المحور $x$ في الفترة $\left[2 , 3\right]$

      $$\begin{gathered} A={\int }_2^3(x^2-2x) dx \\ =(\frac{x^3}{3}-\frac{2x^2}{2}) \overline{)\begin{array}{c}3\\ 2\end{array} } \\ = (\frac{x^3}{3}-x^2)\overline{)\begin{array}{c}3\\ 2\end{array} } \\ = (\frac{{\left(3\right)}^3}{3}-{\left(3\right)}^2) - (\frac{{\left(2\right)}^3}{3}-{\left(2\right)}^2) \\ = (\frac{27}{3}-9) - \left(\frac{8}{3}-4\right) \\ = \left(9-9\right)-\left(\frac{8}{3}-\frac{12}{3}\right) \\ = \frac{ 4}{3} \end{gathered}$$

    إذن المساحة هي:$\left(\frac{4}{3}\right)$ وحدة مربعة.

 

15)أجد مساحة المنطقة المحصورة بين منحنى الاقتران، والمحور $x$ ، والمستقيم $x=-1$ .

 

             الحل:

          يبين الشكل أن منحنى الاقتران يقع فوق المحور $x$، في الفترة $\left[-1 , 0\right]$

    $$\begin{gathered} A={\int }_{-1}^{ 0}(x^2-2x) dx \\ = (\frac{x^3}{3}-x^2)\overline{)\begin{array}{c} 0\\ -1\end{array} } \\ = (\frac{{\left(0\right)}^3}{3}-{\left(0\right)}^2) - (\frac{{\left(-1\right)}^3}{3}-{(-1)}^2) = 0 - (\frac{-1}{3}-1) \\ = \frac{1}{3}+1 \\ =\frac{1}{3}+\frac{3}{3} \\ = \frac{4}{3} \end{gathered}$$

 

        إذن المساحة هي: $\left(\frac{4}{3}\right)$ وحدة مربعة.

 

---

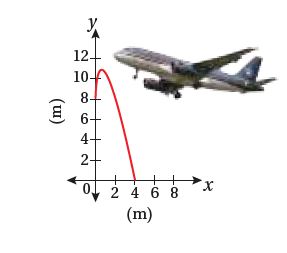
16)يبين التمثيل البياني الآتي شكل السطح العلوي لجناح طائرة،

     ممثلًا بالمعادلة: $y = 8 + 8\sqrt{x} -6x$،حيث:$0 \le x \le 4$ .

     أجد مساحة السطح العلوي لجناح الطائرة.

     الحل:

     يبين الشكل أن منحنى الاقتران يقع فوق المحور $x$ ، في الفترة $\left[0 , 4\right]$

 

   $$\begin{gathered} A={\int }_0^{4 }\left(8+8\sqrt{x}-6x\right) dx \\ ={\int }_0^{4 } \left(8+8\left(x^{\frac{1}{2}}\right)-6x\right) dx \\ = (8x + \frac{8 x^{{\displaystyle \frac{3}{2}}}}{{\displaystyle \frac{3}{2}}}-\frac{6x^2}{2})\overline{)\begin{array}{c}4\\ 0\end{array} } \\ = (8x +\frac{16}{3}\sqrt{x^3} -3x^2)\overline{)\begin{array}{c}4\\ 0\end{array} } \\ =(8\left(4\right) +\frac{16}{3}\sqrt{{\left(4\right)}^3} -3{\left(4\right)}^2)-\left(8\right(0) +\frac{16}{3}\sqrt{{\left(0\right)}^3} -3{\left(0\right)}^2) =32 +\frac{16}{3}\left(8\right)-3\left(16\right) \\ =32 + \frac{128}{3}-48 \end{gathered}$$

                                                                                                                                                                                                                                                                     $$\begin{gathered} = -16+\frac{128}{3} \\ = -\frac{48}{3}+\frac{128}{3} \\ =\frac{80}{3} \end{gathered}$$

إذن مساحة السطح العلوي لجناح الطائرة هي: $\left(\frac{80}{3}\right)$ متر مربع.

 

 

---

مهارات التفكير العليا:

 

17) تحدٍّ: يبين الشكل التالي منحنى الاقتران : $y= kx\left(4-x\right)$.

              إذا كانت مساحة المنطقة المحصورة بين منحنى الاقتران  والمحور $x$ هي 32 وحدة مربعة ،

             فأجد قيمة الثابت $k$.

الحل:

الخطوة 1: جد الإحداثي $x$ لنقاط تقاطع منحنى الاقتران مع المحور $x$

                  بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                  $$\begin{gathered} kx(4-x)=0 \\ kx=0 or 4-x=0 \\ \to x=0 , x= 4 \end{gathered}$$

                 إذن تمثل الإحداثيات $0 , 4$ حدود التكامل.

                 

الخطوة 2:  يبين الشكل أن منحنى الاقتران يقع فوق المحور $x$ في الفترة $\left[0 , 4\right]$

 

الخطوة 3: جد قيمة الثابت $k$ مستخدمًا المساحة عن طريق التكامل:

                   $$\begin{gathered} A ={\int }_0^4 kx (4-x) dx \\ ={\int }_0^4 (4k x-k{x}^2) dx \\ = (\frac{4k x^2}{2}-\frac{k{x}^3}{3})\overline{)\begin{array}{c}4\\ 0\end{array} } \\ = (2 k x^2-\frac{k}{3}{x}^3)\overline{)\begin{array}{c}4\\ 0\end{array} } \\ 32=(2 k {\left(4\right)}^2-\frac{k}{3}{\left(4\right)}^3)-(2 k {\left(0\right)}^2-\frac{k}{3}{\left(0\right)}^3) \\ 32= (32 k -\frac{64}{3}k)-0 \\ 32=32 (k -\frac{2}{3}k) \\ 1=\frac{1}{3}k \\ \to k = 3 \end{gathered}$$

 

---

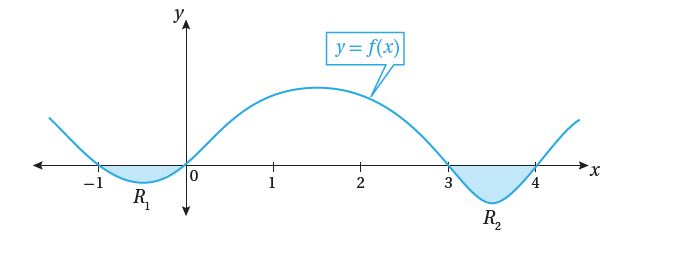
18) تبرير: يبين الشكل التالي منحنى الاقتران $f\left(x\right)$ .إذا كانت مساحة المنطقة $R_1$ هي وحدتين مربعتين ،

                ومساحة المنطقة $R_2$  هي 3 وحدات مربعة ، وكان:${\int }_0^{4}f\left(x\right) dx = 10$ ،

                فأجد ${\int }_{-1}^{ 3}f\left(x\right) dx$ ، مبررًا إجابتي.

 

الحل:

الخطوة 1: استخدم المساحة $R_1$ المعطاة بالسؤال لإيجاد ${\int }_{-1}^0 f\left(x\right) dx$.

                 من الشكل  $R_1$ تقع تحت المحور $x$ ،لذلك:

                  $$\begin{gathered} R_1 =- {\int }_{-1}^{0}f\left(x\right) dx \\ 2 = - {\int }_{-1}^{0}f\left(x\right) dx \\ -2 = {\int }_{-1}^{0}f\left(x\right) dx \end{gathered}$$

 

الخطوة 2: استخدم المساحة $R_2$ المعطاة بالسؤال لإيجاد ${\int }_3^4 f\left(x\right) dx$.

                  من الشكل $R_2$ تقع تحت المحور $x$ ، لذلك:

                 $$\begin{gathered} R_2 =- {\int }_3^{4}f\left(x\right) dx \\ 3=- {\int }_3^{4}f\left(x\right) dx \\ -3 = {\int }_3^{4}f\left(x\right) dx \end{gathered}$$

 

الخطوة 3: جد ${\int }_0^{3}f\left(x\right) dx$ باستخدام تجزئة التكامل :

                 $$\begin{gathered} {\int }_0^{4}f\left(x\right) dx = {\int }_0^{3}f\left(x\right) dx + {\int }_3^{4}f\left(x\right) dx \\ 10 = {\int }_0^{3}f\left(x\right) dx + \left(-3\right) \\ 10+3 = {\int }_0^{3}f\left(x\right) dx \\ 13 = {\int }_0^{3}f\left(x\right) dx \end{gathered}$$

 

الخطوة 4: جد ${\int }_{-1}^{ 3}f\left(x\right) dx$باستخدام تجزئة التكامل :

                  $$\begin{gathered} {\int }_{-1}^{ 3}f\left(x\right) dx = {\int }_{-1}^{ 0}f\left(x\right) dx + {\int }_0^{3}f\left(x\right) dx \\ = \left(-2\right) + \left(13\right) \\ = 11 \end{gathered}$$

 

 

---

كتاب التمارين صفحة 12 :

 

أجد مساحة المنطقة المظللة في كل من التمثيلات البيانية الآتية:

 

 

 

$$\begin{gathered} A = - {\int }_0^1 (x^2-x) dx + {\int }_1^2 (x^2-x) dx \\ =-(\frac{x^3}{3}-\frac{x^2}{2}) \overline{)\begin{array}{c}1\\ 0\end{array}} + (\frac{x^3}{3}-\frac{x^2}{2}) \overline{)\begin{array}{c}2\\ 1\end{array}} \\ =\left((-\frac{{\left(1\right)}^3}{3}+\frac{{\left(1\right)}^2}{2})-\left(0\right)\right) + \left((\frac{{\left(2\right)}^3}{3}-\frac{{\left(2\right)}^2}{2})-(\frac{{\left(1\right)}^3}{3}-\frac{{\left(1\right)}^2}{2})\right) \\ = (-\frac{1}{3}+\frac{1}{2}) + (\frac{8}{3}-\frac{4}{2}-\frac{1}{3}+\frac{1}{2}) \\ =-\frac{1}{3}+\frac{1}{2}+\frac{7}{3}-\frac{3}{2} \\ = \frac{6}{3}-\frac{2}{2} \\ =2-1 \\ =1 \end{gathered}$$

 

---

 

 

 

$$\begin{gathered} A = {\int }_4^9 \frac{1}{\sqrt{x}} dx ={\int }_4^9 x^{-\frac{1}{2}} dx \\ =\left(\frac{x^{{\displaystyle \frac{1}{2}}}}{{\displaystyle \frac{1}{2}}}\right) \overline{)\begin{array}{c}9\\ 4\end{array}} =\left(2 \sqrt{x}\right) \overline{)\begin{array}{c}9\\ 4\end{array}} \\ =2 \left(\sqrt{9} -\sqrt{4}\right) \\ =2 (3 - 2) \\ =2 \end{gathered}$$

 

---

 

 

$$\begin{gathered} A = {\int }_{-1}^{ 4} \left(4+3x-x^2\right) dx \\ =(4x +\frac{3x^2}{2}-\frac{x^3}{3}) \overline{)\begin{array}{c} 4\\ -1\end{array}} \\ =\left(4\left(4\right)+\frac{3{\left(4\right)}^2}{2}-\frac{{\left(4\right)}^3}{3}\right)- (4\left(-1\right)+\frac{3{\left(-1\right)}^2}{2}-\frac{{\left(-1\right)}^3}{3}) \\ =\left(16 + 24-\frac{64}{3}\right)- \left(-4 +\frac{3}{2}+\frac{1}{3}\right) \\ = 40 - \frac{64}{3}+4 -\frac{3}{2} -\frac{1}{3} \\ = 44 -\frac{65}{3}-\frac{3}{2} \\ = \frac{264}{6}-\frac{130}{6}-\frac{9}{2} \\ =\frac{125}{6} \end{gathered}$$

 

---

 

 

$$\begin{gathered} A =- {\int }_{-1}^{ 0} (3x^2+x-2) dx \\ =-(\frac{3x^3}{3}+\frac{x^2}{2}-2x) \overline{)\begin{array}{c} 0\\ -1\end{array}} \\ = \left(-x^3-\frac{x^2}{2}+2x\right) \overline{)\begin{array}{c} 0\\ -1\end{array}} \\ =0-\left(-{\left(-1\right)}^3-\frac{{\left(-1\right)}^2}{2}+2\left(-1\right)\right) \\ =-\left(1-\frac{1}{2}-2\right) \\ =-(\frac{1}{2}-\frac{4}{2}) \\ = - \left(-\frac{3}{2}\right) \\ =\frac{3}{2} \end{gathered}$$

---

 

 

 

$$\begin{gathered} A = {\int }_{-1}^{ 1} (1-x^2) dx \\ =(x -\frac{x^3}{3}) \overline{)\begin{array}{c} 1\\ -1\end{array}} \\ =(1-\frac{{\left(1\right)}^3}{3})- (-1-\frac{}{3}) \\ =(\frac{3}{3} -\frac{1}{3})- (-\frac{3}{3} +\frac{1}{3}) \\ = \frac{2}{3}-\left(-\frac{2}{3}\right) \\ = \frac{2}{3}+\frac{2}{3} \\ =\frac{4}{3} \end{gathered}$$

---

 

 

$$\begin{gathered} A = - {\int }_0^1 (x^2-1) dx + {\int }_1^2 (x^2-1) dx \\ =-(\frac{x^3}{3}-x) \overline{)\begin{array}{c}1\\ 0\end{array}} + (\frac{x^3}{3}-x) \overline{)\begin{array}{c}2\\ 1\end{array}} \\ =\left((-\frac{}{3}+1)-0\right) + \left((\frac{{\left(2\right)}^3}{3}-2)-(\frac{{\left(1\right)}^3}{3}-1)\right) \\ = (-\frac{1}{3}+\frac{3}{3}) + (\frac{8}{3}-\frac{4}{2}-\frac{1}{3}+\frac{3}{3}) \\ =\frac{2}{3}+\frac{10}{3}-\frac{4}{2} \\ = \frac{12}{3}-\frac{4}{2} \\ =4-2 \\ =2 \end{gathered}$$

 

---

 

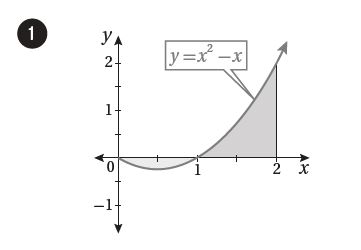
7) أجد مساحة المنطقة المحصورة بين منحنى الاقتران:$f\left(x\right)=3x^2 - 3$ ، و المحور $x$

الحل:

الخطوة 1: جد الإحداثي $x$  لنقاط تقاطع منحنى الاقتران مع المحور $x$

                 بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                  $$\begin{gathered} 3x^2-3 =0 \\ 3(x^2-1)=0 \\ (x-1)\left(x+1\right)=0 \\ \left(x-1\right)=0 or \left(x+1\right)=0 \\ \to x=1 , x=-1 \end{gathered}$$

             هذه الإحداثيات تمثل حدود التكامل.

 

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور x

                  باختيار عدد يقع ضمن الفترة وليكن $0$ ونعوضه في قاعدة الاقتران:

                    $$\begin{gathered} f\left(0\right)=3{\left(0\right)}^2 - 3 \\ f\left(0\right)= -3 < 0 \end{gathered}$$

                 إذن منحنى الاقتران يقع تحت المحور x لأن نتيجة التعويض سالبة.

 

الخطوة 3: جد المساحة عن طريق التكامل:

                  $$\begin{gathered} A =- {\int }_{-1}^{ 1} (3x^2-3) dx \\ =-(\frac{3x^3}{3}-3x) \overline{)\begin{array}{c} 1\\ -1\end{array}} \\ = (-x^3+3x) \overline{)\begin{array}{c} 1\\ -1\end{array}} \\ =\left(-{\left(1\right)}^3+3\left(1\right)\right)-(-{\left(-1\right)}^3+3\left(-1\right)) \\ =(-1+3) -\left(1-3\right) \\ =2-\left(-2\right) \\ =4 \end{gathered}$$

 

---

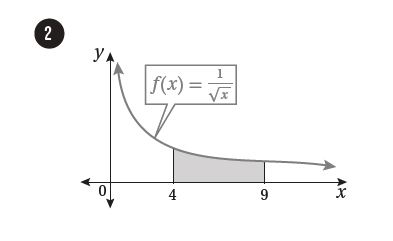
8) أجد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right)=x^3 - 5x^2 -6x$، و المحور $x$

الحل:

الخطوة 1: جد الإحداثي $x$ لنقاط تقاطع منحنى الاقتران مع المحور $x$

                   بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

                    $$\begin{gathered} x^3-5x^2 -6x=0 \\ x(x^2-5x-6)=0 \\ x(x-6)(x+1)=0 \\ x=0 or (x-6)=0 or \left(x+1\right)=0 \\ \to x=0 , x=6 , x=-1 \end{gathered}$$

                هذه الإحداثيات تمثل حدود التكامل.

 

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور x

                  باختيار عدد يقع ضمن الفترة $\left[-1 , 0\right]$ وليكن$\left(-\frac{1}{2}\right)$ ونعوضه في قاعدة الاقتران:

                  $$\begin{gathered} f\left(x\right)={\left(x\right)}^3-5{\left(x\right)}^2 -6\left(x\right) \\ f(-\frac{1}{2})={(-\frac{1}{2})}^3-5{(-\frac{1}{2})}^2 -6(-\frac{1}{2}) \\ =-\frac{1}{8}-\frac{5}{4}+3 \\ = -\frac{1}{8}-\frac{10}{8}+\frac{24}{8} \\ = \frac{13}{8}>0 \end{gathered}$$

 

               إذن منحنى الاقتران في الفترة $[-1 , 0]$ يقع فوق المحور x لأن نتيجة التعويض موجبة.

 

             وباختيار عدد يقع ضمن الفترة $\left[0 , 6\right]$ وليكن 1 ونعوضه في قاعدة الاقتران:

                              $$\begin{gathered} f\left(x\right)={\left(x\right)}^3-5{\left(x\right)}^2 -6\left(x\right) \\ f\left(1\right)={\left(1\right)}^3-5{\left(1\right)}^2 -6\left(1\right) \\ =1-5-6 \\ = -4-6 \\ = -10<0 \end{gathered}$$

                           إذن منحنى الاقتران يقع تحت المحور x  في الفترة $[0 , 6]$ لأن نتيجة التعويض سالبة.

 

 

الخطوة 3: جد المساحة عن طريق التكامل:

                   $$\begin{gathered} A = {\int }_{-1}^{ 0} (x^3-5x^2-6x) dx- {\int }_1^6 (x^3-5x^2-6x) dx \\ =(\frac{x^4}{4}-\frac{5x^3}{3}-\frac{6x^2}{2}) \overline{)\begin{array}{c} 0\\ -1\end{array}} -(\frac{x^4}{4}-\frac{5x^3}{3}-\frac{6x^2}{2}) \overline{)\begin{array}{c} 6\\ 0\end{array} } \\ = (\frac{x^4}{4}-\frac{5x^3}{3}-3x^2) \overline{)\begin{array}{c} 0\\ -1\end{array}} +(-\frac{x^4}{4}+\frac{5x^3}{3}+3x^2) \overline{)\begin{array}{c} 6\\ 0\end{array} } \\ = 0-(\frac{{\left(-1\right)}^4}{4}-\frac{5{\left(-1\right)}^3}{3}-3{\left(-1\right)}^2) +(-\frac{{\left(6\right)}^4}{4}+\frac{5{\left(6\right)}^3}{3}+3{\left(6\right)}^2)-0 \\ =-(\frac{1}{4}+\frac{5}{3}-3)+(-\frac{ 1296}{4}+\frac{ 1080}{3}+108) \\ = \left(-\frac{3}{12}-\frac{20}{12}+\frac{36}{12}\right)+\left(-324+360+108\right) \\ =\frac{13}{12}+144 \\ =\frac{ 13}{12}+\frac{ 1728}{12} \\ =\frac{1741}{12} \end{gathered}$$

 

---

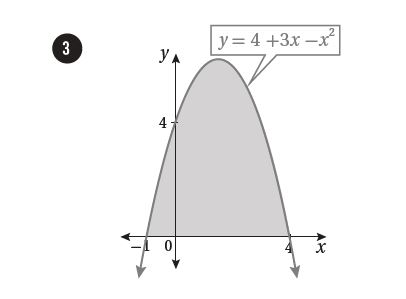
9) أجد مساحة المنطقة المحصورة بين منحنى الاقتران:$f\left(x\right)=x^2 \left(2-x\right)$ ، و المحور $x$

الحل:

الخطوة 1: جد الإحداثي $x$ لنقاط تقاطع منحنى الاقتران مع المحور $x$

                  بمساواة قاعدة الاقتران بالصفر وحل المعادلة الناتجة:

 

                   $$\begin{gathered} x^2 \left(2-x\right)=0 \\ {x}^2=0 or (2-x)=0 \\ \to x=0 , x=2 \end{gathered}$$

               هذه الإحداثيات تمثل حدود التكامل.

 

 

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور x

                  باختيار عدد يقع ضمن الفترة $\left[0 , 2\right]$ وليكن 1 ونعوضه في قاعدة الاقتران:

                  $$\begin{gathered} f\left(1\right)=1^2 (2-1) \\ f\left(1\right)=1>0 \end{gathered}$$

 

                 إذن منحنى الاقتران يقع فوق المحور x لأن نتيجة التعويض موجبة.

 

الخطوة 3: جد المساحة عن طريق التكامل

                                         $$\begin{gathered} A = {\int }_0^2 \left(x^2\left(2-x\right)\right) dx = {\int }_0^2 (2x^2-x^3) dx \\ =(\frac{2x^3}{3}-\frac{x^4}{4}) \overline{)\begin{array}{c} 2\\ 0\end{array}} \\ =(\frac{2{\left(2\right)}^3}{3}-\frac{{\left(2\right)}^4}{4})-0 \\ =\frac{16}{3}-\frac{16}{4} \\ =\frac{64}{12}-\frac{48}{12} \\ =\frac{16}{12}=\frac{4}{3} \end{gathered}$$

 

---

أتدرب:صفحة 41:

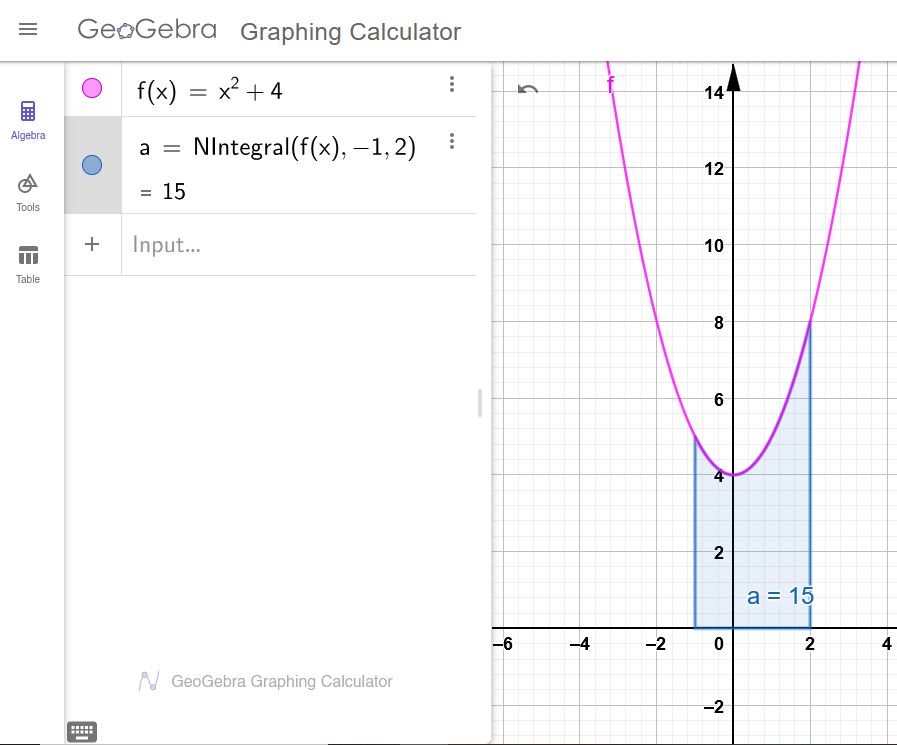
1) أجد مساحة المنطقة المحصورة بين منحنى الاقتران:  $f\left(x\right)=x^2+4$ ،

    والمحور $x$ ، والمستقيمين: $x=-1$ و $x=2$

 

الحل: باستخدام برمجية جيوجبرا :

 

إذن مساحة المنطقة هي تقريبًا: 15 وحدة مربعة.

---

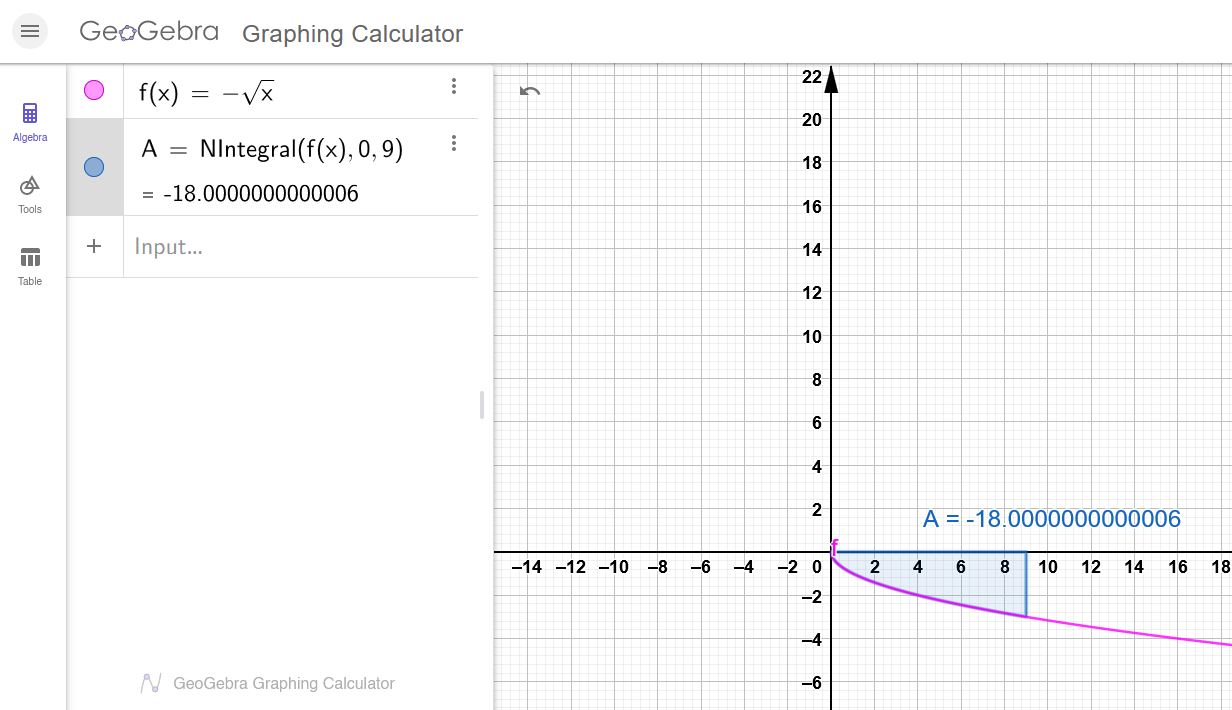
2) أجد مساحة المنطقة المحصورة بين منحنى الاقتران:  $f\left(x\right)=-\sqrt{x}$ ، والمحور $x$ ، والمستقيم: $x=9$

 

الحل: باستخدام برمجية جيوجبرا :

    إذن مساحة المنطقة هي تقريبًا: 18 وحدة مربعة.

---

تمت الأسئلة