رياضيات9 فصل أول

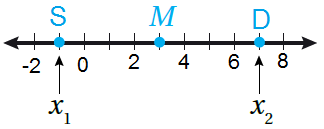
المسافة في المُستوى الإحداثيّ

Distance in the Coordinate Plane

فكرة الدرس :  •  إيجادُ المسافةِ بين نقطتين في المُستوى الإحداثيِّ.

                        •  إيجاد نقطة مُنتصف قطعة مستقيمة في المُستوى الإحداثِيّ.

 

أولًا  : المسافة بين نقطتين

المسافةُ بينَ نقطتَيْنِ على خطِّ الأعدادِ هِيَ طولُ القطعةِ المستقيمةِ الواصلةِ بين هاتين النقطتين بحيث تُمثّلان نهايتيِ القطعة ، ويمكن

استعمال إحداثِيّ كلّ من النقطتين لإيجاد المسافةِ بينَهُما.

•• مفهومٌ أساسيٌّ (صيغةُ المسافةِ على خطِّ الأعدادِ)

بالكلماتِ : المسافة بين نقطتَيْن على خطِّ الأعدادِ هِيَ القيمةُ المُطلقةُ للفرقِ بين إحداثِيَّيْهِما. بالرُّموز : إذا كانَ إحداثيُّ النقطة A على خطِّ  الأعداد هو x1 وإحداثيُّ النقطة B هو x2  ، فإنَّ :   $AB = |x_2 - x_1| or AB = |x_1 - x_2|$

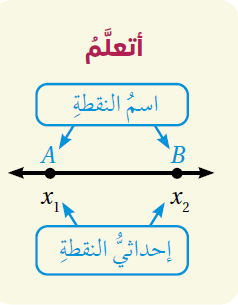•• رُموز رياضيّة :  يُرمَز للقطعة المستقيمة التي نقطة بدايتِها A ونهايتِها B بالرَّمز $\overline{AB}$ أمّا طولُها فيُرمز له بالرَّمز AB

مثال : 

أستعمل خطّ الأعداد الآتي لأجد AE . 

الحل : 

بما أنّ إحداثِيّ النقطة A هُوَ 8 - ، وإحداثِيَّ النقطة E هُو 2 ، فإنّ : 

$AE=|x_2-x_1|$	صيغةُ المسافةِ على خطِّ الأعدادِ
$AE=|2-(-8\left)\right|$	بتعويض
$AE=10$	بالتبسيطِ

---

•• مفهوم أساسي (صيغةُ المسافةِ في المُستوى الإحداثِيِّ)

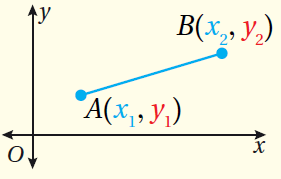المسافةُ بينَ النقطتَيْنِ ( A(x1 , y1 وَ ( B(x2 , y2 ، هِيَ :           $AB = \sqrt{{(x_2 - x_1)}^2 + {(y_2 - y_1)}^2}$

•• أتعلَّمُ : مِنَ الأسهل إيجاد طول القطعة المُستقيمة الأُفقيَّةِ في المُستوى الإحداثيِّ باستعمال صيغة المسافة على خطِّ الأعداد ، وذلك بإيجادِ القيمةِ المُطلقةِ للفرقِ بينَ الإحداثِيِّ x لكلٍّ مِنْ نُقطَتَيْ نهايَتَيِ القطعة، ولإيجاد طول القطعة المستقيمةِ العموديَّة أَجِدُ القيمة المُطلقة للفرق بين الإحداثيِّ y لكلٍّ مِن نقطَتَيْ نهايَتَيِ القطعة.

مثال : 

أَجِدُ المسافة بين النقطتين ( 4 , B (-3 وَ ( 1 , A (5 ، مُقَرِّبًا إجابتي لأقرب جُزء من عشرة.

الحل : 

$AB = \sqrt{{(x_2 - x_1)}^2 + {(y_2 - y_1)}^2}$	صيغةُ المسافةِ في المُستوى الإحداثِيِّ
$AB = \sqrt{{(-3 - 5)}^2 + {(4 - (1\left)\right)}^2}$	بتعويضِ $(x_1, y_1)=(5,1) , (x_2 , y_2)=(-3,4)$
$AB = \sqrt{{(-8)}^2 + {\left(3\right)}^2}$	بالتبسيطِ
$AB = \sqrt{73}$	بإيجادِ مُرَبَّعِ كلِّ عددٍ، والجمعِ
$AB \approx 8.5$	باستعمالِ الآلةِ الحاسبةِ

إذنْ، المسافةُ بينَ النقطتَيْنِ A وَ B هِيَ 8.5 وحدةً تقريبًا.

---

•• أتعلَّمُ : عندَ إيجادِ المسافةِ بينَ نقطتَيْنِ في المُستوى الإحداثِيِّ لا يكونُ ترتيبُ الإحداثِيَّيْنِ x وَ y في كلِّ مجموعةٍ مِنَ الأقواسِ مهمًّا.

ثانيًا : نقطةُ مُنتصفِ القطعةِ المستقيمةِ

نقطةُ مُنتصفِ القطعةِ المستقيمةِ هِيَ النقطةُ التي تقعُ في مُنتصفِ المسافةِ بينَ نقطتَيْ نهايَتَيِ القطعةِ المستقيمةِ.

•• مفهومٌ أساسيٌّ (صيغةُ نقطةِ المُنتصفِ على خطِّ الأعدادِ)

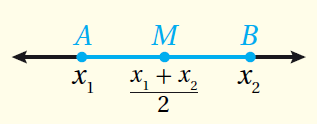إذا كانَ إحداثِيُّ النقطةِ A على خطِّ الأعدادِ هُوَ x1  وَإحداثِيُّ النقطةِ B هُوَ x2 ، وكانتْ M نقطةَ مُنتصفِ AB ، فإنَّ  إحداثِيَّ M هُوَ :                                         $\frac{x_1 + x_2}{2}$

مثال : 

إذا كانَ إحداثيّا نقطتَيْ نهايَتَيْ $\overline{SD}$ هُما 1- وَ 7، فَأَجِدُ إحداثِيَّ نقطةِ مُنتصفِ$\overline{SD}$

الحل : 

	$\frac{x_1 + x_2}{2}$	صيغةُ نقطةِ المُنتصفِ على خطِّ الأعدادِ
	$= \frac{7 + (-1)}{2}$	بتعويضِ $x_1=7, x_2=-1$
	$= \frac{6}{2} = 3$	بالتبسيطِ

إذن ، إحداثِيُّ نقطة المُنتصف هُو 3 

---

مثال : 

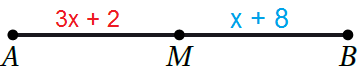في الشكلِ المُجاورِ ، إذا كانتْ M نقطةَ مُنتصفِ $\overline{AB }$ ، فَأَجِدُ طولَ AM

 

 

 

 الحل : 

الخُطوة 1 : أجد قيمة x   

$\overline{AM} \cong \overline{MB}$	تعريفُ نقطةِ مُنتصفِ قطعةٍ مستقيمةٍ
$AM = MB$	تعريفُ تطابقِ القطعِ المستقيمةِ
$3x + 2 = x + 8$	بالتعويضِ
$3x = x + 6$	بطرح 2 من طَرَفَيِ المُعادلةِ
$2x = 6$	بطرحِ x مِنْ طَرَفَيِ المُعادلةِ
$x = 3$	بقسمة طرفي المعادلة على 2

 

 

 

 

 

 

الخُطوةُ 2 : أَجِدُ طولَ $\overline{AM}$

$AM = 3x + 2$	طول $\overline{AM}$
$= 3\times 3 + 2$	بتعويض x = 3
$= 11$	بالتبسيط

إذن ، طول $\overline{MB}$ هوَ 11 وحدة طول.

---

يمكنُ إيجادُ إحداثِيَّيْ نقطةِ مُنتصفِ قطعةٍ مستقيمةٍ في المُستوى الإحداثِيِّ بإيجادِ الوسطِ الحسابيِّ لكلٍّ مِنَ الإحداثِيِّ x والإحداثِيِّ y لِنُقطتَيْ نهايَتَيْهِ.

•• مفهومٌ أساسيٌّ (صيغةُ نقطةِ المُنتصفِ في المُستوى الإحداثِيِّ)

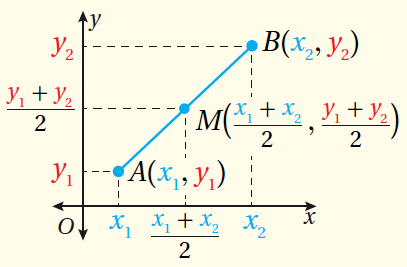إذا كانت $B(x_2 , y_2) و A(x_1 , y_1)$ نقطتَيْنِ في المُستوى الإحداثِيِّ ، وَ M نقطةَ مُنتصفِ AB ، فإنَّ إحداثِيَّيْ M  هُما                         $M (\frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2})$

مثال  : 

أَجِدُ إحداثيّيِ النقطة M ، التي تُمَثلُ مُنتصف AB ؛ حيث $B(5 , 7) و A(1 , 3)$.

الحل : 

$M (\frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2})$	صيغةُ نقطةِ المُنتصفِ في المُستوى الإحداثِيِّ
$M (\frac{1 + 5}{2} , \frac{3 + 7}{2})$	بتعويض $(x_1, y_1)=(1,3),(x_2, y_2)=(5,7)$
$M (3 , 5)$	بالتبسيطِ

 

 

 

 

 

•• أتعلَّمُ : ترتيبُ إحداثِيَّيْ نقطتَيْ نهايَتَيِ القطعةِ المستقيمةِ ليس مهمًّا عندَ إيجادِ إحداثِيَّيْ نقطةِ مُنتصفِ قطعةٍ مستقيمةٍ.

---

يمكن إيجاد إحداثِيَّيْ نقطة نهاية قطعة مستقيمة إذا عُلم إحداثِيّا نقطة النهاية الأُخرى للقطعة وإحداثيّا نقطة المُنتصف.

مثال :

إذا كانتْ ( 5 , M (3 نقطةَ مُنتصفِ $\overline{RT}$ ؛ حيثُ ( 6 , R (-2  ، فأجِد إحداثيَّي النقطة T.

الحل : 

الخطوة 1 : أُعَوِّضُ الإحداثياتِ المعلومة في صيغةِ نقطة المُنتصف في المُستوى الإحداثِيِّ.

أفترِضُ أنَّ $R (x_{2 }, y_2) و T (x_1 , y_1)$

$M (\frac{x_1 + x_2}{2} , \frac{y_2 +y_2}{2}) = M (3 , 5)$	صيغةُ نقطةِ المُنتصفِ في المُستوى الإحداثِيِّ
$M (\frac{-2 + x_2}{2} , \frac{6 +y_2}{2}) = M (3 , 5)$	بتعويض $(x_1,y_1)=(-2,6)$

 

 

 

 

الخطوة 2 : أكتبُ مُعادلَتَيْنِ ، وَأَحُلُّهُما لإيجادِ إحداثِيَّيْ T

أجد y2	أجد x2
$\frac{6+y_2}{2}=5\to 6+y_2=10\to y_2=4$	$\frac{-2+x_2}{2}=3\to -2+x_2=6\to x_2=8$

إذنْ، إحداثيّا النقطةِ T هُما ( 4 , 8).

---

 

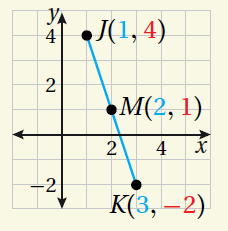•• أتعلَّمُ :  يُمكِنُني التحقُّقُ مِنْ معقوليَّةِ الإجابةِ بتمثيلِ النقاطِ الثلاثةِ في المُستوى الإحداثِيِّ ، وملاحظةِ أنَّ  المسافةَ بينَ J  وَ M تَظهَرُ مساويةً للمسافةِ بينَ M وَ K