رياضيات 9 فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 41

أجدُ قِيَمَ النسبِ المُثلَّثيةِ الثلاثِ للزاويةِ T في المُثلَّثِ المُجاوِرِ.   الحل:  الخطوةُ 1: أستعملُ نظريةَ فيثاغورس لإيجادِ t

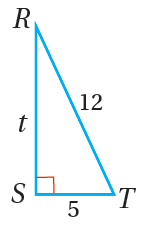نظريةُ فيثاغورس	$s^2=r^2+t^2$
بتعويض $s=12,r=5$	${12}^2=5^2+t^2$
بالتبسيطِ	$144=25+t^2$
بطرح 25 من طرفي المعادلة	$t^2=119$
بأخذِ الجذرِ التربيعيِّ لطرفيِ المعادلةِ	$t^{ }=\pm \sqrt[]{119}$

بما أنَّ الطولَ لا يُمكِنُ أنْ يكونَ سالبًا، فإنَّ $t^{ }=\sqrt[]{119}$

الخطوةُ 2: أجدُ النسبَ المُثلَّثيةَ الثلاثَ.

$\tan T=\frac{t}{r}=\frac{\sqrt{119}}{ 5}$

$\cos T=\frac{r}{s}=\frac{5}{12}$

$\sin T=\frac{t}{s}=\frac{\sqrt[]{119}}{12}$

---

أتحقق من فهمي صفحة 43

أجدُ قيمةَ كلٍّ ممّا يأتي باستعمالِ الآلةِ الحاسبةِ، مُقرِّبًا إجابتي إلى أقربِ ثلاثِ منازلَ عشريةٍ: 

$\mathit{a}\mathbf{)} \sin 36°=0.588 \mathbf{ }\mathit{b}\mathbf{)} \cos 70°=0.342 \mathbf{ }\mathit{c}\mathbf{)} \tan 82°=7.115$

---

أتحقق من فهمي صفحة 44

أجدُ قياسَ $\angle A$ في كلٍّ ممّا يأتي، مُقرِّبًا إجابتي إلى أقربِ منزلةٍ عشريةٍ واحدةٍ:

$\mathit{a}\mathbf{)} \sin A=\frac{ 4}{9}$

$m\angle A= {\sin }^{-1}\left(\frac{4}{9}\right)=26.4°$

 

$\mathit{b}\mathbf{)} \cos A=0.64$

$m\angle A={\cos }^{-1}( 0.64)=50.2°$

 

$\mathit{c}\mathbf{)} \tan A=0.707$

$m\angle A={\tan }^{-1}(0.707)=35.3°$

---

أتحقق من فهمي صفحة 46 

في المُثلَّثِ المُجاوِرِ، إذا كانَ $\cos A=\frac{4}{5}$ ، فأجدُ  sin A .

الحل : 

مُتطابِقةُ فيثاغورس	$si{n}^{2}A+co{s}^{2}A=1$
بتعويضِ $\cos A=\frac{4}{5}$	$si{n}^{2}A+{\left(\frac{4}{5}\right)}^2=1$
بالتربيعِ	$si{n}^{2}A+\frac{16}{25}=1$
بطرحِ $\frac{16}{25}$  من طرفي المعادلة	$si{n}^{2}A=\frac{9}{25}$
بأخذِ الجذرِ التربيعيِّ للطرفينِ	$sinA=\pm \frac{3}{5}$

بما أنَّ جيبَ الزاويةِ A في المُثلَّثِ قائمِ الزاويةِ ABC هوَ ناتجُ قسمةِ طولِ الضلعِ المقابل على الوترِ، وبما أنَّ الأطوالَ لا يُمكِنُ أنْ تكونَ سالبةً، فإنَّ sin A قيمةٌ موجبةٌ ؛ أيْ $sinA=\frac{3}{5}$

---

أتحقق من فهمي صفحة 46 

إذا كانَ $\sin 70°=0.9397$، فأجدُ $\cos 20°$

الحل: 

تعريفُ الجيبِ وجيبِ التمامِ للزوايا المُتتامَّةِ	$\sin A=\cos (90°-A)$
بتعويضِ $A=70°$	$\sin 70°=\cos (90°-70°)$
بالتبسيطِ	$\sin 70°=\cos 20°$
بتعويضِ $\sin 70°=0.9397$	$\therefore cos20°=0.9397$

---

أسئلة أتدرب وأحل المسائل 

أجدُ قِيَمَ النسبِ المُثلَّثيةِ الثلاثِ للزاويةِ A في كلٍّ ممّا يأتي، تاركًا إجابتي في صورةِ كسرٍ :

الحل : 

1) أجد طول AB باستخدام نظرية فيثاغورس : AB = 12  

$\tan A=\frac{BC}{AB}=\frac{5}{12}$

$\cos A=\frac{AB}{AC}=\frac{12}{13}$

$\sin A=\frac{BC}{AC}=\frac{5}{13}$

 

2) أجد طول AB باستخدام نظرية فيثاغورس : AB = 25  

$\tan A=\frac{BC}{AC}=\frac{7}{24}$

$\cos A=\frac{AC}{AB}=\frac{24}{25}$

$\sin A=\frac{BC}{AB}=\frac{7}{25}$

 

3) أجد طول AB باستخدام نظرية فيثاغورس : $AB=\sqrt[]{161}$

$\tan A=\frac{BC}{AB}=\frac{8}{\sqrt[]{161}}$

$\cos A=\frac{AB}{AC}=\frac{\sqrt[]{161}}{15}$

$\sin A=\frac{BC}{AC}=\frac{8}{15}$

---

أجدُ قيمةَ كلٍّ ممّا يأتي باستعمالِ الآلةِ الحاسبةِ، مُقرِّبًا إجابتي إلى أقربِ ثلاثِ منازلَ عشريةٍ : 

$\mathbf{6}\mathbf{)} \sin 90° = 1$	$\mathbf{5}\mathbf{)}\mathbf{ }\sin 67.2° \approx 0.913$	$\mathbf{4}\mathbf{)} \sin 43° \approx 0.682$
$\mathbf{ }\mathbf{9}\mathbf{)} \cos 90° = 0$	$\mathbf{8}\mathbf{)} \cos 22° \approx 0.927$	$\mathbf{7}\mathbf{)}\mathbf{ }\cos 80° \approx 0.174$
$\mathbf{12}\mathbf{)}\mathbf{ }\tan 30° \approx 0.577$	$\mathbf{11}\mathbf{)} \tan 45° = 1$	$\mathbf{10}\mathbf{)} \tan 20° \approx 0.364$
$\mathbf{15}\mathbf{)} 9 \cos 8° \approx 8.912$	$\mathbf{14}\mathbf{)} 7 \tan 52° \approx 8.96$	$\mathbf{13}\mathbf{)} 4 \sin 63° \approx 3.564$
$\mathbf{18}\mathbf{)}\mathbf{ }\frac{7}{cos 60°}=14$	$\mathbf{17}\mathbf{)}\mathbf{ }\frac{3}{tan 64°}\approx 1.463$	$\mathbf{16}\mathbf{)}\mathbf{ }\frac{5}{sin 31°}\approx 9.708$

 

---

أجدُ قياسَ $\angle B$  في كلٍّ ممّا يأتي، مُقرِّبًا إجابتي إلى أقربِ منزلةٍ عشريةٍ واحدةٍ :

$\mathbf{19}\mathbf{)} \sin B=0.5$

$m\angle B={\sin }^{-1}(0.5)=30°$

 

$\mathbf{20}\mathbf{)} \sin B=0.999$

$m\angle B={\sin }^{-1}(0.999)\approx 87.4°$

 

$\mathbf{21}\mathbf{)} \sin B=0.877$

$m\angle B=s{\mathrm{in}}^{-1}(0.877)\approx 61.3°$

---

أجدُ قياسَ  $\angle N$في كلٍّ ممّا يأتي، مُقرِّبًا إجابتي إلى أقربِ منزلةٍ عشريةٍ واحدةٍ : 

$\mathbf{22}\mathbf{)}\mathbf{ }\cos N=0.2$

$m\angle N={\cos }^{-1}(0.2)\approx 78.5°$

 

$\mathbf{23}\mathbf{)}\mathbf{ }\cos N=0.5$

$m\angle N={\cos }^{-1}(0.5)=60°$

 

$\mathbf{24}\mathbf{)}\mathbf{ }\cos N=0.999$

$m\angle N={\cos }^{-1}(0.999)\approx 2.6°$

---

أجدُ قياسَ  $\angle M$ في كلٍّ ممّا يأتي، مُقرِّبًا إجابتي إلى أقربِ منزلةٍ عشريةٍ واحدةٍ:

$\mathbf{25}\mathbf{)} \tan M=0.6$

$m\angle M={\tan }^{-1}(0.6)\approx 31°$

 

$\mathbf{26}\mathbf{)} \tan M=2.67$

$m\angle M={\tan }^{-1}(2.67)\approx 69.5°$

 

$\mathbf{27}\mathbf{)} \tan M=4.38$

$m\angle M={\tan }^{-1}(4.38)\approx 77.1°$

---

28)  في المُثلَّثِ المُجاوِرِ، إذا كانَ $\sin A=\frac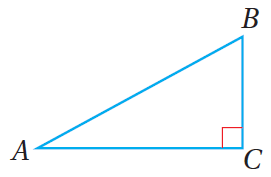{8}{17}$ ، فأجدُ  cos A.

الحل : 

$si{n}^{2}A+co{s}^{2}A=1$

${\left(\frac{8}{17}\right)}^2+co{s}^{2}A=1$

$\frac{64}{289}+co{s}^{2}A=1$

$co{s}^{2}A=\frac{225}{289}$

$cosA=\pm \frac{15}{17}$

ولأنّ A زاوية حادة فإنّ $cosA=\frac{15}{17}$

---

29)  إذا كانَ 0.57358 = °cos 55 ، فأجدُ $\sin 35°$. 

الحل : 

تعريفُ الجيبِ وجيبِ التمامِ للزوايا المُتتامَّةِ	$\cos A=\sin (90°-A)$
بتعويضِ $A=55$	$\cos 55=\sin (90°-55)$
بالتبسيطِ	$\cos 55=\sin 35$
بتعويضِ 0.57358=°cos 55	$\therefore sin35°=0.57358$

---

30) إذا كانَ 0.9781 = °sin 78 ، فأجدُ °cos 12 ، و $\sin 12°$.

الحل : 

$\cos 12°=\sin 78°=0.9781$   (تعريفُ الجيبِ وجيبِ التمامِ للزوايا المُتتامَّةِ)

الآن أجد $\sin 12°$ من متطابقة فيثاغورس 

$si{n}^{2}A+co{s}^{2}A=1$

$si{n}^{2}12°+co{s}^{2}12°=1$

$si{n}^{2}12°+{(0.9781)}^2=1$

$si{n}^{2}12°+0.95667961=1$

$si{n}^{2}12°=0.04332039$

$sin12°=\pm \sqrt{0.04332039}\approx 0.208$

---

مهاراتُ التفكيرِ العليا

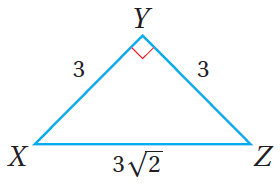
تبريرٌ: أستعملُ المعلوماتِ المعطاةَ في الشكلِ المُجاوِرِ للإجابةِ عنِ الأسئلةِ الآتيةِ، مُبرِّرًا إجابتي: 31) أُحدِّدُ النسبَ المُثلَّثيةَ المتساويةَ في الشكلِ. 32) ما قياسُ كلٍّ منَ الزاويةِ X ، والزاويةِ Z؟ 33) أكتبُ استنتاجًا بناءً على إجابتي عنِ السؤالينِ السابقينِ.

الحل : 

31) $m\angle X=m\angle Z$ (زوايا القاعدة في مثلث متطابق الضلعين ) ، إذن الزاويتين لهما نسب متساوية . 

$\sin X=\frac{YZ}{XZ}=\frac{3}{3\sqrt[]{2}}=\frac{1}{\sqrt[]{2}}$

$\sin Z=\frac{XY}{XZ}=\frac{3}{3\sqrt[]{2}}=\frac{1}{\sqrt[]{2}}$

$\cos X=\frac{YX}{XZ}=\frac{3}{3\sqrt[]{2}}=\frac{1}{\sqrt[]{2}}$

$\cos Z=\frac{YZ}{XZ}=\frac{3}{3\sqrt[]{2}}=\frac{1}{\sqrt[]{2}}$

 

32) بما أنّ المثلث XYZ قائم الزاوية ، إذن مجموع زوايا القاعدة يساوي $90°$ ، وبما أنهما زاويتين متطابقتين في القياس ، إذن قياس كل من الزاويتين يساوي $45°$ 

33) أستنتج أنّ :  $sin45°=cos45°=\frac{1}{\sqrt[]{2}}$ 

---

تبريرٌ: إذا كانَ ΔLMN قائمَ الزاويةِ في M، فأُثبِتُ صحَّةَ كلِّ متباينةٍ ممّا يأتي:

$\mathbf{34}\mathbf{)} \sin L<1 \mathbf{ }\mathbf{ }\mathbf{35}\mathbf{)} \cos L<1$

الحل: 

34) $\sin L=\frac{l}{m}$ وبما أنّ الضلع المقابل للزاوية L أقل من طول الوتر ، أي جيب الزاوية L هو عبارة عن كسر عادي بسطه أقل من مقامه فقيمته أقل من 1 إذن؛ $\sin L<1$ 35) $\cos L=\frac{n}{m}$  وبما أنّ الضلع المجاور للزاوية L أقل من طول الوتر ، أي جيب تمام الزاوية L هو عبارة عن كسر عادي بسطه أقل من مقامه فقيمته أقل من 1 إذن؛ $\cos L<1$

---

36) تحدٍّ: مُعتمِدًا الشكلَ الآتيَ، أُثبِتُ أنَّ $\tan A=\frac{\sin A}{\cos A}$

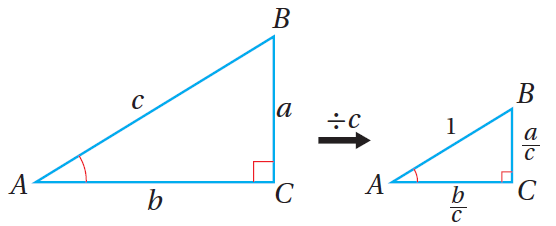
الحل : 

في المثلث ABC 

$\sin A=\frac{a}{c} \cos A=\frac{b}{c} tanA=\frac{a}{b}$

الشق الأيمن للمعادلة : 

$\frac{\sin A}{\cos A}=\frac{\frac{a}{\cancel{c}}}{\frac{b}{\cancel{c}}}=\frac{a}{b}=tanA$

أجد النسب المثلثية الثلاثة عند قسمة أطوال أضلاع المثلث على c 

$\sin A=\frac{\frac{a}{c}}{1}=\frac{a}{c} \cos A=\frac{\frac{b}{c}}{1}=\frac{b}{c} tanA=\frac{\frac{a}{\cancel{c}}}{\frac{b}{\cancel{c}}}=\frac{a}{b}$

الشق الأيمن للمعادلة : 

$\frac{\sin A}{\cos A}=\frac{\frac{a}{\cancel{c}}}{\frac{b}{\cancel{c}}}=\frac{a}{b}=t\mathrm{an}A$

---

أسئلة كتاب التمارين

أجدُ قِيَمَ النسبِ المُثلَّثيةِ الثلاثِ للزاويةِ E في كلٍّ ممّا يأتي، تاركًا إجابتي في صورةِ كسرٍ : 

الحل : 

1) أجد طول DF باستخدام نظرية فيثاغورس: DF = 9 

$\tan E=\frac{DF}{FE}=\frac{9}{12}=\frac{3}{4}$

$\cos E=\frac{EF}{DE}=\frac{12}{15}=\frac{4}{5}$

$\sin E=\frac{DF}{DE}=\frac{9}{15}=\frac{3}{5}$

 

2) أجد طول DE باستخدام نظرية فيثاغورس: DE = 37 

$\tan E=\frac{DF}{FE}=\frac{12}{35}$

$\cos E=\frac{EF}{DE}=\frac{35}{37}$

$\sin E=\frac{DF}{DE}=\frac{12}{37}$

 

3) أجد طول DE باستخدام نظرية فيثاغورس: $EF=\sqrt[]{507}$

$\tan E=\frac{DF}{EF}=\frac{13}{\sqrt[]{507}}$

$\cos E=\frac{EF}{DE}=\frac{\sqrt[]{507}}{26}$

$\sin E=\frac{DF}{DE}=\frac{13}{26}=\frac{1}{2}$

---

أجدُ قيمةَ كلٍّ ممّا يأتي باستعمالِ الآلةِ الحاسبةِ، مُقرِّبًا إجابتي إلى أقربِ ثلاثِ منازلَ عشريةٍ : 

$\mathbf{6}\mathbf{)} \sin 72°\approx 0.951$	$\mathbf{5}\mathbf{)} \sin 17°\approx 0.292$	$\mathbf{4}\mathbf{)} \sin 0°=0$
$\mathbf{9}\mathbf{)} \cos 29°\approx 0.875$	$\mathbf{8}\mathbf{)} \cos 82°\approx 0.139$	$\mathbf{7}\mathbf{)}\mathbf{ }\cos 7°\approx 0.993$
$\mathbf{12}\mathbf{)} \tan 78°\approx 4.705$	$\mathbf{11}\mathbf{)} \tan 59°\approx 1.664$	$\mathbf{10}\mathbf{)}\mathbf{ }\tan 15°\approx 0.267$
$\mathbf{15}\mathbf{)} 7\cos 52°\approx 4.31$	$\mathbf{14}\mathbf{)} \frac{7}{\cos 32°}\approx 8.254$	$\mathbf{13}\mathbf{)}\mathbf{ }5\tan 80°\approx 28.356$

---

أجدُ قياسَ الزاويةِ في كلٍّ ممّا يأتي، مُقرِّبًا إجابتي إلى أقربِ منزلةٍ عشريةٍ واحدةٍ :  

$\mathbf{16}\mathbf{)} \sin B=0.7245$

$m\angle B={\sin }^{-1}(0.7245)\approx 46.4°$

 

$\mathbf{17}\mathbf{)} \cos C=0.2493$

$m\angle C={\cos }^{-1}(0.2493)\approx 75.6°$

 

$\mathbf{18}\mathbf{)} \tan E=9.4618$

$m\angle E={\tan }^{-1}(9.4618)\approx 84°$

---

19) مُعتمِدًا المعلوماتِ المعطاةَ في الشكلِ المُجاوِرِ، أُحدِّدُ النسبَ المُثلَّثيةَ التي تساوي $\frac{1}{2}$ مما يأتي (أُحدِّدُ جميعَ الخياراتِ المُمكِنةِ):

$sinL cosL sinJ cosJ$

الحل: 

(جيب الزاوية L يساوي 0.5): $\sin L=\frac{JK}{JL}=\frac{2}{4}=\frac{1}{2}$ 

(جيب التمام للزاوية L لا يساوي 0.5) : $\cos L=\frac{LK}{JL}=\frac{2\sqrt[]{3}}{4}=\frac{\sqrt[]{3}}{2}$

(جيب الزاوية J  لا يساوي 0.5): $\sin J=\frac{LK}{JL}=\frac{2\sqrt[]{3}}{4}=\frac{\sqrt[]{3}}{2}$

(جيب التمام للزاوية J يساوي 0.5):  $\cos J=\frac{JK}{JL}=\frac{2}{4}=\frac{1}{2}$

---

20)  أكتشفُ الخطأَ : أُبيِّنُ الخطأَ في الحَلِّ المُجاوِرِ، ثمَّ أُصحِّحُهُ.

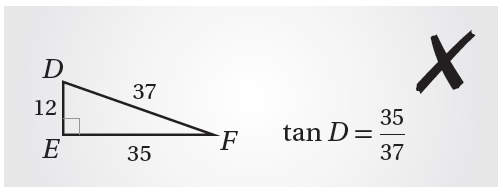
الحل: 

الخطأ بقسمة طول الضلع المقابل للزاوية D على طول الوتر  ، والصحيح : ظل الزاوية D ينتج من قسمة طول الضلع المقابل الزاوية D على طول الضلع المجاور لها ، أي : 

$\tan D=\frac{EF}{ED}=\frac{35}{12}$