رياضيات فصل أول

تعرفنا في الدرس السابق كيفية إيجاد النسب المثلثية لزاوية مرسومة في الوضع القياسي باستعمال احداثيي نقطة تقاطع ضلع انتهائها مع دائرة الوحدة، وسنتعرف في هذا الدرس كيف نجد النسب المثلثية إذا علم قياس الزاوية بالدرجات 

إذا وقع ضلع انتهاء الزاوية $\theta$ في الربع الأول( أي كانت $0°<\theta <90°$)، فإنه يمكن إيجاد النسب المثلثية لهذه الزاوية باستعمال الآلة الحاسبة، أو بما نحفظه من نسب مثلثية للزوايا الخاصة: $\left(30°,45°,60°\right)$

مراجعة المفاهيم 

النسب المثلثية للزاويا الخاصة: 

أما إذا وقع ضلع انتهاء الزاوية $\theta$ المرسومة في الوضع القياسي في أي من الأرباع الثلاثة الأخرى، فإن نسبها المثلثية تكون مرتبطة بالنسب المثلثية للزاوية المرجعية $\theta \text{'}$، وهي الزاوية الحادة المحصورة بين ضلع انتهاء الزاوية $\theta$ والمحور x 

مفهوم أساسي 

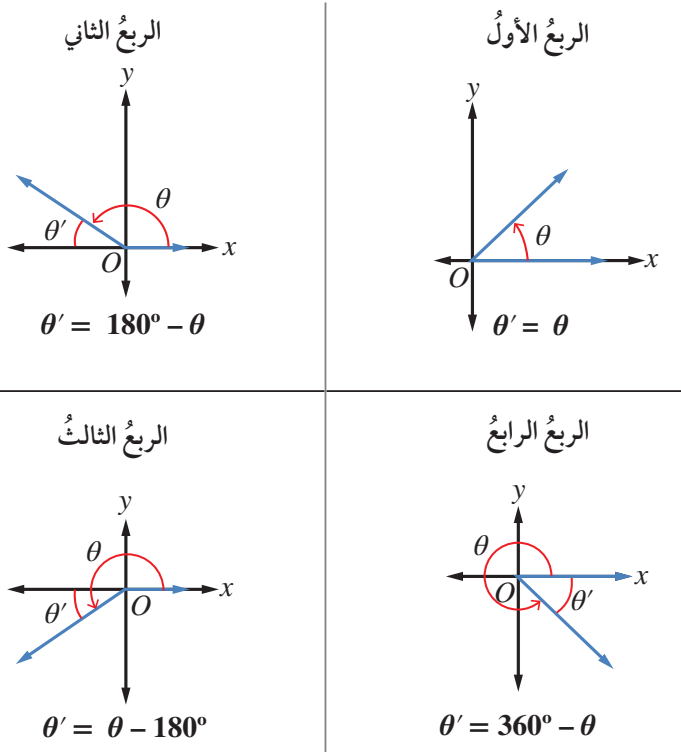
النسب المثلثية للزاوية $\theta$ تساوي النسب المثلثية لزاويتهاالمرجعية $\theta \text{'}$ مع اختلاف الإشارة أحيانا بحسب الربع الذي يقع فيه ضلع انتهاء الزاوية $\theta$

لإيجاد النسب المثلثية لأي زاوية $\theta$، فإننا نتبع الخطوات الثلاث الآتية:  

الخطوة 1: إيجاد الزاوية المرجعية $\theta \text{'}$

الخطوة 2: إيجاد النسبة المثلثية للزاوية المرجعية $\theta \text{'}$

الخطوة 3: تحديد إشارة النسبة المثلثية للزاوية $\theta$ بحسب الربع الذي يقع فيه ضلع انتهائها 

مثال 

أجد قيمة كل مما يأتي: 

$1) \sin 150°$

يقع ضلع الانتهاء للزاوية $150°$ في الربع الثاني؛ لذا استعمل زاويتها المرجعية: 

$$\begin{gathered} \theta \text{'}=180°-\theta \\ =180°-150° \\ =30° \\ sin 150°=sin 30°=0.5 \end{gathered}$$

$2) \cos 225°$

يقع ضلع الانتهاء للزاوية $225°$ في الربع الثالث؛ لذا نستعمل زاويتها المرجعية: 

$$\begin{gathered} \theta \text{'}=\theta -180° \\ =225°-180° \\ =45° \\ cos 225°=-cos 45° \\ =-\frac{\sqrt{2}}{2} \end{gathered}$$

$3) \tan 300°$

يقع ضلع الانتهاء للزاوية $300°$ في الربع الرابع؛ لذا نستعمل زاويتها المرجعية:

$$\begin{gathered} \theta \text{'}=360°-\theta \\ \theta \text{'}=360°-300° \\ =60° \\ tan 300°=-tan 60° \\ =-\sqrt{3} \end{gathered}$$

جميع الزوايا في المثال السابق مرتبطة بزاوية مرجعية مألوفة، مثل: $،60° \mathrm{او،}45°\mathrm{او،}30°$وهي زوايا خاصة عرفنا قيم النسب المثلثية لها. ولكن،كيف نجد النسب المثلثية لأي زوايا أخرى؟ يمكن إيجاد النسبة المثلثية للزاوية المرجعية بالستعمال الآلة الحاسبة، ثم تحديد الإشارة المنسبة تبعا للربع الذي يقع فيه ضلع انتهاء الزاوية 

مثال 

أجد قيمة كل مما يأتي: 

$1) sin 255°$

يقع ضلع الانتهاء للزاوية $255°$ في الربع الثالث؛ لذا استعمل زاويتها المرجعية: 

$$\begin{gathered} \theta \text{'}=\theta -180° \\ \theta \text{'}=255°-180° \\ =75° \\ sin 255°=-sin 75° \end{gathered}$$

ولأن، استعمل الآلة الحاسبة لإيجاد $\sin 75°$ كما يأتي: 

اضغط على مفتاح ، ثم أدخل القيمة 75، ثم اضغط على مفتاح  ، فتظهر النتيجة: 

بالتقريب إلى منزل عشرية، تكون النتيجة: $0.966$

إذن، $\sin 255°\approx -0.966$

يمكن أيضا إيجاد $\sin 255°$ مباشرة باستعمال الآلة الحاسبة من دون إيجاد الزاوية المرجعية على النحو الآتي: 

اضغط على مفتاح ، ثم أدخل القيمة 255، ثم اضغط على مفتاح ، فتظهر النتيجة: 

بالتقريب إلى ثلاث منازل عشرية، تكون النتيجة $-0.966$، وهي النتيجة نفسها التي توصلت إليها آنفا 

$2) \tan 168°$

اضغط على مفتاح ، ثم أدخل القيمة 168، ثم اضغط على مفتاح ، فتظهر النتيجة: 

بالتقريب إلى ثلاث منازل عشرية، تكون النتيجة: $-0.213$

إذن، $\tan 168°\approx -0.213$

يمكن استعمال الآلة الحاسبة لإيجاد قياس أي زاوية حادة (في الربع الأول) علمت إحدى نسبها المثلثية، وذلك باستعمال معكوس النسبة المثلثية. فإذا علم جيب الزاوية استعمل معكوس الجيب $\left({\sin }^{-1}\right)$، وإذا علم جيب تمام الزاوية استعمل معكوس جيب التمام $\left({\cos }^{-1}\right)$، وإذا علم ظل الزاوية استعمل معكوس الظل $\left({\tan }^{-1}\right)$. وبالطريقة نفسها، يمكن إيجاد قياس أي زاوية في الأرباع الثلاثة الباقية باستعمال مفهوم الزاوية المرجعية وإشارات النسب المثلثية في الأرباع الأربعة 

مثال 

أجد قيمة (أو قيم) $\theta$ في ما يأتي، علما بأن $:0°\le \theta \le 360°$

$$\begin{gathered} 1) \sin \theta =0.98 \\ \theta ={\sin }^{-1}\left(0.98\right) \end{gathered}$$

ولأن، استعمل الآلة الحاسبة لإيجاد ${\sin }^{-1}\left(0.98\right)$ كما يأتي: 

وبالقريب إلى منزلة عشرية واحدة، تكون النتيجة:$78.5°$، وهي زاوية مرجعية لزاوية أخرى، لأنها تقع في الربع الأول. وبما أن الجيب موجب في ربعين (الأول والثاني فقط)، فإن الزاوية الأخرى $\theta$ تكون في الربع الثاني، ويمكن إيجادها باستعمال العلاقة بين الزاوية المرجعية والزاوية المناظرة في الربع الثاني التي تعرفتها آنفا 

$$\begin{gathered} \theta \text{'}=180°-\theta \\ \theta \text{'}=78.5° \\ 78.5°=180°-\theta \\ \theta =101.5° \end{gathered}$$

إذن، $\theta =101.5°\mathrm{او،}\theta =78.5°$

$$\begin{gathered} 2) \tan \theta =-1.2 \\ \theta ={\tan }^{-1}\left(-1.2\right) \end{gathered}$$

ولأن، استعمل الآلة الحاسبة لإيجاد ${\tan }^{-1}\left(-1.2\right)$ كما يأتي: 

وبالتقريب إلى منزلة عشرية واحدة، تكون النتيجة: $50.2°$؛ ولأن الظل يكون سالبا في ربعين فقط (الثاني والرابع)؛ فإن الزاوية $50.2°$ ليست من الحلول، وإنما زاوية مرجعية لها 

إذا استعملنا العلاقة بين الزاوية المرجعية والزوايا المناظرة في الربعين الثاني والرابع، فإننا سنجد هاتين الزاويتين: 

$$\begin{gathered} \mathrm{زاوية} \mathrm{الربع} \mathrm{الثاني}: °8.129=°2.50-°180 \\ \mathrm{زاوية} \mathrm{الربع} \mathrm{الرابع}: °8.309=°2.50-°360 \end{gathered}$$

مثال:

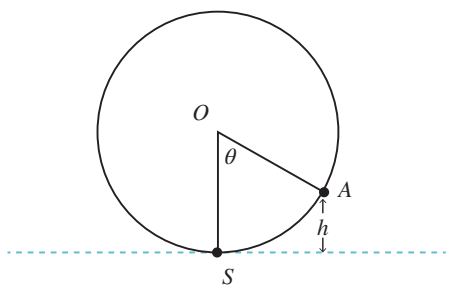
يمثل الشكل الاتي ناعورة ماء تدور بسرعة ثابتة وتمثل$S$  في الشكل اخفض نقطة تبلغها الناعورة تحت الماء في حين تمثل النقطة  $O$مركز الناعورة اذا دارت الناعورة بزاوية $\theta$ فان  ارتفاع صندوق الماء الذي موقعه النقطة $A$ عن اخفض نقطة تبلغها الناعورة يعطى بالعلاقة : $h=7.5-7.5\cos \theta$ حيث$\left(h\right)$   الارتفاع بالامتار   اجد طول قطر الناعورة.

الحل : عندما يصل الصندوق الى النقطة الواقعة فوق ممم  مباشرة فان ارتفاعه عن اخفض موقع له  يساوي طول قطر الناعورة ويكون قياس $\theta$ في تلك اللحظة $180°$ :

$$\begin{gathered} h=7.5-7.5cos180 \\ =7.5-7.5\left(-1\right) \\ =7.5+7.5=15 \end{gathered}$$

اذا طول قطر الناعورة هو  :  $15m$