الدرس الثاني: النمو والاضمحلال الأسي
سنتعرف في درس النمو والاضمحلال الأسي إلى:
1. اقتران النمو الأسي وخصائصه.
2. اقتران الاضمحلال الأسي وخصائصه.
3. الربح المركب والربح المركب المستمر.
4. الاقتران الأسي الطبيعي
أولا: اقتران النمو الأسي
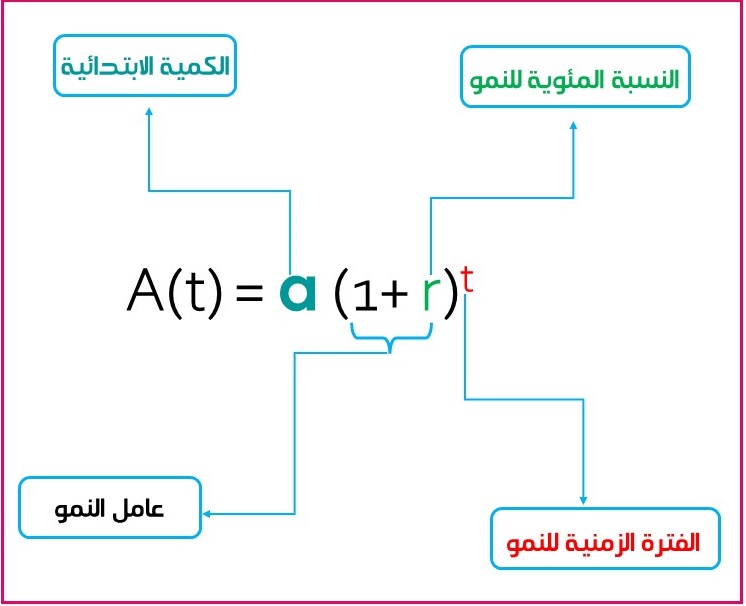
هو اقتران أسي يتزايد بنسبة مئوية ثابتة في فترات زمنية متساوية.
ويعبر عنه بالرموز :
حيث: : الكمية الابتدائية
: الفترة الزمنية
:النسبة المئوية للنمو في فترة زمنية محددة
: هو أساس العبارة الأسية: عامل النمو
اقتران النمو الأسي : هو إحدى صور الاقتران الأسي ، حيث استعمل المقدار بدلًا من ، واستعمل بدلًا من
|
اقتران النمو الأسي: بالكلمات: هو كل اقتران أسي يتزايد بنسبة مئوية ثابتة في فترات زمنية متساوية
بالرموز:
|
مثال: في دراسة شملت الزيادة السكانية في أحد الأحياء السكنية، تبين أن عدد السكان يزداد بنسبة تبلغ نحو %23 سنويًا:
a) اكتب اقتران النمو الأسي الذي يمثل عدد سكان الحي بعد t سنة، علمًا بأن عددهم عند بدء الدراسة هو 425 نسمة.
b) جد عدد السكان بعد 8 سنوات من بدء الدراسة
الحل:
a) اكتب اقتران النمو الأسي الذي يمثل عدد السكان بعد t سنة
ألاحظ أن: (عند قسمة عدد على 100 تتحرك الفاصلة العشرية الى اليسار بمقادر منزلتين - بعدد أصفار المقام).
| اقتران النمو الأسي | |
| بتعويض a=425, r=0.23 | |
| بالتبسيط |
اقتران النمو الأسي الذي يمثل عدد السكان بعد t سنة هو:
b) جد عدد السكان بعد 8 سنوات من بدء الدراسة:
لإيجاد عدد السكان بعد 8 سنوات، عوض t=8 باقتران النمو الأسي:
| اقتران النمو الأسي للسكان | |
| بتعويض t=8 | |
| باستعمال الآلة الحاسبة |
عدد السكان بعد 8 سنوات تقريبا 2227 نسمة.
ثانيا: اقتران الاضمحلال الأسي
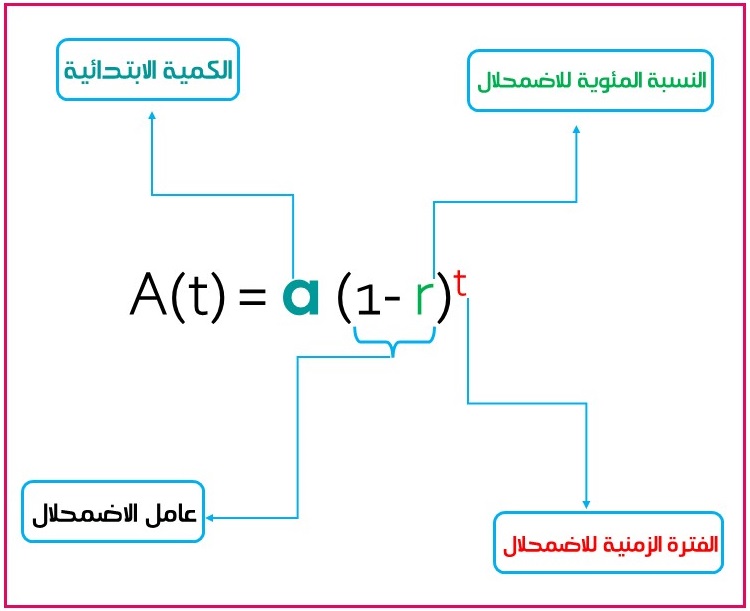
هو اقتران أسي يتناقص بنسبة مئوية ثابتة في فترات زمنية متساوية.
ويعبر عنه بالرموز :
حيث: : اقتران الاضمحلال الأسي
: الكمية الابتدائية
: الفترة الزمنية
: النسبة المئوية للاضمحلال في فترة زمنية محددة
: هو أساس العبارة الأسية: عامل الاضمحلال
|
اقتران الاضمحلال الأسي: بالكلمات: هو اقتران أسي يتناقص بنسبة مئوية ثابتة في فترات زمنية متساوية
بالرموز:
|
مثال: اشترى أحمد دراجة نارية بمبلغ 8950 JD. إذا كان ثمن الدراجة يقل بنسبة %4.5 سنويًا، فأجب عن السؤالين الآتيين:
a) اكتب اقتران الاضمحلال الأسي لثمن السيارة بالدنانير بعد t سنة.
b) جد ثمن السيارة بعد 6 سنوات .
الحل:
a) اقتران الاضمحلال الأسي لثمن السيارة بعد t سنة.
ألاحظ أن:
( عند قسمة العدد العشري على 100، تتحرك الفاصلة باتجاه اليسار منزلتين -بعدد أصفار المقام)
| اقتران الاضمحلال الأسي | |
| بتعويض | |
| بالتبسيط |
اقتران الاضمحلال الأسي لثمن الدراجة بعد t سنة هو:
b) ثمن الدراجة بعد 6 سنوات.
| اقتران الاضمحلال الأسي | |
| بتعويض t=6 | |
| باستعمال الآلة الحاسبة |
ثمن الدراجة بعد 6 سنوات هو تقريبًا 6790 JD
ثالثا: الربح المركب
أحد التطبيقات الحياتية للنمو الأسي، وهو الفائدة المستحقة على مبلغ الاستثمار الأصلي الذي يسمى رأس المال، والفوائد المستحقة سابقًا.
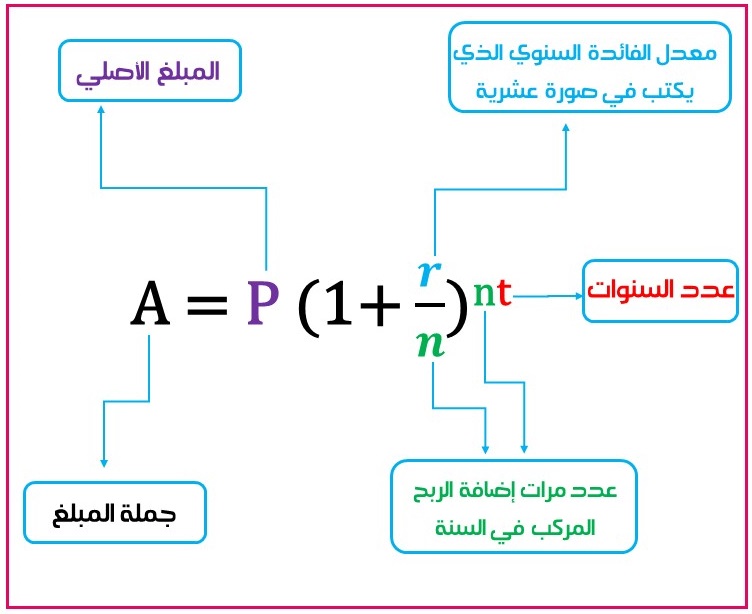
بالرموز:
حيث: : جملة المبلغ
: المبلغ الأصلي
: معدل الفائدة السنوي الذي يكتب في صورة عشرية
: عدد مرات إضافة الربح المركب في السنة.
: عدد السنوات
|
الربح المركب: بالكلمات: يمكن حساب جملة المبلغ المستحق في حالة الربح المركب باستعمال الصيغة الآتية:
بالرموز:
|
مثال: يستثمر ماجد مبلغ 8500 JD في شركة عقارية، بنسبة ربح مركب تبلغ % 6.5 ، وتضاف كل 4 أشهر.جد جملة المبلغ بعد 7 سنوات.
الحل:
تضاف نسبة الربح كل 4 أشهر، يعني 3 مرات في السنة أي إن:
|
P=8500, r=6.5%=0.065 n= t=7 |
بتحديد المعطيات |
| صيغة الربح المركب | |
| بتعويض المعطيات | |
| بالتبسيط باستخدام الآلة الحاسبة |
جملة المبلغ بعد 7 سنوات تقريبًا 13342 JD
رابعا: الاقتران الأسي الطبيعي
الاقتران الأسي الطبيعي هو اقتران أسي أساسه الأساس الطبيعي (العدد النيبيري)الذي يساوي تقريبًا ...2.718281828 والذي رمزه .
الاقتران الأسي الطبيعي بالرموز:
خصائص الاقتران الأسي الطبيعي هي نفسها خصائص الاقتران ، حيث
1) الاقتران متزايد لأن
2)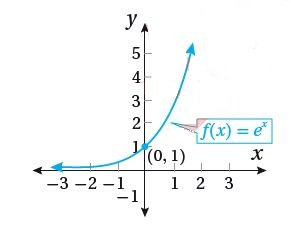
3) له مقطع عند 1
4) خط التقارب الأفقي هو محور
5) وهو اقتران واحد لواحد باستخدام اختبار الخط الأفقي.
من تطبيقات الاقتران الأسي الطبيعي: الربح المركب المستمر
خامسا: الربح المركب المستمر
الربح المركب المستمر هو عملية حساب جملة المبلغ بعد إضافة الربح المركب إلى رأس المال عددًا لا نهائيًّا من المرات في السنة.
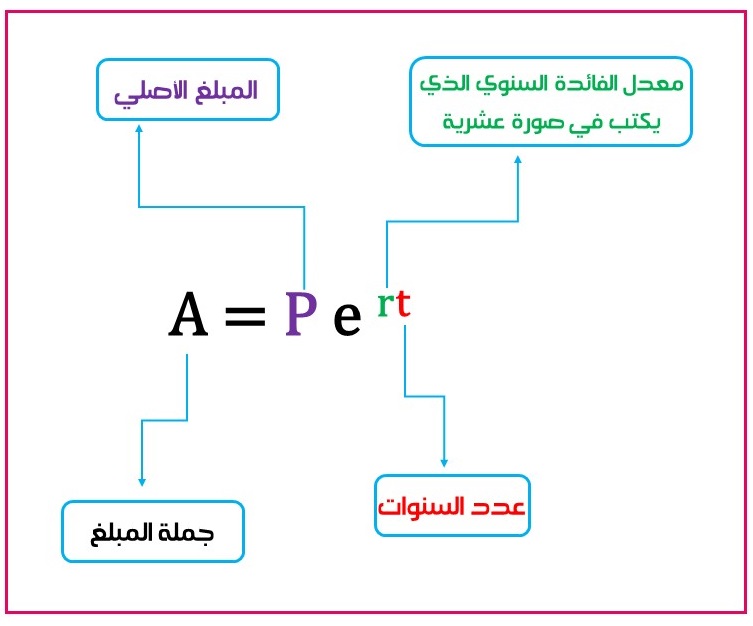
يمكن حساب الربح المركب المستمر باستخدام الصيغة الآتية:
حيث:
:جملة المبلغ
: المبلغ الأصلي
: معدل الفائدة المستمر الذي يكتب في صورة عشرية
: عدد السنوات
|
الربح المركب المستمر : بالكلمات: يمكن حساب جملة المبلغ المستحق في حالة الربح المركب المستمر باستعمال الصيغة الآتية:
بالرموز:
|
مثال: أودعت رؤى مبلغ 7900 JD في حساب بنكي، بنسبة ربح مركب مستمر مقدارها % 5.3 ، جد جملة المبلغ بعد 10 سنوات.
الحل:
| صيغة الربح المركب | |
|
بالتعويض:
|
|
| باستعمال الآلة الحاسبة |
إذن جملة المبلغ بعد 10 سنوات تقريبًا: 13422 JD