النهايات والاتصال - حل اسئلة الدرس - الصف الأول ثانوي أدبي - رياضيات أدبي فصل ثاني - مدرسة جواكاديمي

حلول أسئلة كتاب الطالب وكتاب التمارين

حلول أسئلة أتحقق من فهمي

أتحقق من فهمي صفحة 30

أجد قيمة كل نهاية ممّا يأتي (إنْ وُجِدت) بيانيًا وعدديًا :

a) $\lim_{x \to 1} f (x)$ ، حيثُ: $f (x) = x^{2}$ . b) $\lim_{x \to - 3} h (x)$ ، حيثُ: $h (x) = {\begin{cases} x + 2, - 5 \leq x < - 3 \\ 1, x > - 3 \end{cases}$

الحل:

تعويض مباشر في الاقتران

$a) \lim_{x \leftarrow 1} f (x) = \lim_{x \to 1} (x^{2})$ $= {(1)}^{2} = 1$

النهاية من جهة اليمين

النهاية من جهة اليسار

بما أن $\lim_{x \to - 3^{+}} h (x) \neq \lim_{x \to - 3^{-}} h (x)$

إذن النهاية غير موجودة عند $(x = - 3)$

$b) \lim_{x \to - 3^{+}} h (x) = \lim_{x \to - 3^{+}} (1) = 1 \lim_{x \to - 3^{-}} h (x) = \lim_{x \to - 3^{-}} (x + 2) = - 3 + 2 = - 1$

أتحقق من فهمي صفحة 32

أستعمل الخصائص الجبرية للنهايات لإيجاد قيمة كل نهاية ممّا يأتي:

$a) \lim_{x \to - 1} (3 x^{2} - 4 x - 2) b) \lim_{x \to 1} \frac{\sqrt{3 x^{2} + 1}}{2 x - 5}$

الحل :

$a) \lim_{x \to - 1} (3 x^{2} - 4 x - 2) = \lim_{x \to - 1} (3 x^{2}) - \lim_{x \to - 1} (4 x) - \underset{x \to - 1}{\lim (2)} = 3 {(\underset{x \to - 1}{\lim x})}^{2} - 4 \lim_{x \to - 1} x - \lim_{x \to - 1} 2 = 3 {(- 1)}^{2} - 4 (- 1) - 2 = 3 + 4 - 2 = 5$

b) \lim_{x \to 1} \frac{\sqrt{3 x^{2} + 1}}{2 x - 5} = \frac{\lim_{x \to 1} \sqrt{3 x^{2} + 1}}{\lim_{x \to 1} (2 x - 5)} = \frac{\sqrt{\lim_{x \to 1} (3 x^{2} + 1)}}{\lim_{x \to 1} (2 x - 5)} = \frac{\sqrt{4}}{- 3} = \frac{- 2}{3}

أتحقق من فهمي صفحة 34

أجد قيمة كل نهاية ممّا يأتي باستعمال التعويض المباشر إنْ كان ذلك مُمكِنًا، وإلّا فأذكر السبب :

$a) \lim_{x \to - 2} (5 x^{2} - 6 x - 15) b) \lim_{x \to 2} \frac{x^{2} - x - 2}{x + 3} c) \lim_{x \to 5} \frac{x^{2} - 25}{x - 5}$

الحل :

a) \underset{x \to - 2}{\lim (5 x^{2} - 6 x - 15)} = 5 {(- 2)}^{2} - 6 (- 2) - 15 = 20 + 12 - 15 = 17

b) \lim_{x \to 2} \frac{x^{2} - x - 2}{x + 3} = \frac{2^{2} - 2 - 2}{2 + 3} = \frac{0}{5} = 0

$c) \lim_{x \to 5} \frac{x^{2} - 25}{x - 5} = \frac{0}{0}$

لا يمكن إيجاد النهاية باستخدام التعويض المباشر لأن ناتج التعويض = $\frac{0}{0}$

أتحقق من فهمي صفحة 35

أجد قيمة كل نهاية ممّا يأتي:

$a) \lim_{x \to - 2} \frac{x^{2} - x - 6}{x + 2} b) \lim_{x \to 4} \frac{16 - x^{2}}{2 x - 8}$

الحل :

$a) \lim_{x \to - 2} \frac{x^{2} - x - 6}{x + 2}$

$= \lim_{x \to - 2} \frac{(x - 3) (x + 2)}{x + 2} = \lim_{x \to - 2} (x - 3) = - 2 - 3 = - 5$

التعويض المباشر يعطي

\frac{0}{0}

، لذا نلجأ للتحليل ، واختصار العوامل المشتركة بين البسط والمقام ، ثم التعويض بقيمة x = - 2

$b) \lim_{x \to 4} \frac{16 - x^{2}}{2 x - 8}$

$= \lim_{x \to 4} \frac{\overset{- 1}{(4 - x)} (4 + x)}{2 (x - 4)}$

$= \lim_{x \to 4} \frac{- 1 (4 + x)}{2}$

$= \frac{- 1 (4 + 4)}{2} = - 4$

التعويض المباشر يعطي

\frac{0}{0}

، لذا نلجأ للتحليل إلى العوامل واختصار العوامل المشتركة بين البسط والمقام ، ثم التعويض بقيمة x = 4

أتحقق من فهمي صفحة 37

أُحدِّد إذا كان كل اقتران ممّا يأتي متصلً عند قيمة $x$ المعطاة، مُبرِّرًا إجابتي:

$a) g (x) = \frac{x^{3} + 1}{x + 1}, x = - 1 b) h (x) = \{\begin{cases} x - 1, x < 3 \\ 5 - x, x \geq 3 \end{cases}, x = 3$

الحل :

$(x = - 1)$ لا تنتمي لمجال الاقتران g(x) ؛ لأنها صفرًا للمقام ، لذا الاقترانg(x) غير متصل عند $(x = - 1)$	$a) g (x) = \frac{x^{3} + 1}{x + 1}, x = - 1$

	$b) h (x) = \{\begin{cases} x - 1, & x < 3 \\ 5 - x, & x \geq 3 \end{cases}, x = 3$
نجد قيمة الاقتران عند $(x = 3)$	$h (3) = 5 - 3 = 2$
نجد النهاية من جهة اليمين	$\lim_{x \to 3^{+}} h (x) = \lim_{x \to 3^{+}} (5 - x) = 5 - 3 = 2$
نجد النهاية من جهة اليسار	$\lim_{x \to 3^{-}} h (x) = \lim_{x \to 3^{-}} (x - 1) = 3 - 1 = 2$
بما أن : $h (3) = \lim_{x \to 3} h (x)$ ، إذن الاقتران h(x) متصل عند $(x = 3)$

حلول أسئلة أتدرب وأحل المسائل

أستعمل التمثيل البياني المجاور لإيجاد قيمة كل نهاية ممّا يأتي (إنْ وُجِدت):

$2) \lim_{x \to 2^{-}} h (x)$	$1) \lim_{x \to 2^{+}} h (x)$

$\underset{x \to 1}{4) \lim} h (x)$	$3) \lim_{x \to 2} h (x)$

$6) \lim_{x \to - 3} h (x)$	$5) \lim_{x \to - 2} h (x)$

الحل :

$1) \underset{x \to 2^{+}}{l i m} h (x) = 2$	$2) \underset{x \to 2^{-}}{l i m} h (x) = 1$

$3) \underset{x \to 2}{l i m} h (x)$ غير موجودة	$\underset{x \to 1}{4) l i m} h (x) = - 1$

$5) \underset{x \to - 2}{l i m} h (x) = 0.5$	$6) \underset{x \to - 3}{l i m} h (x) = 1$

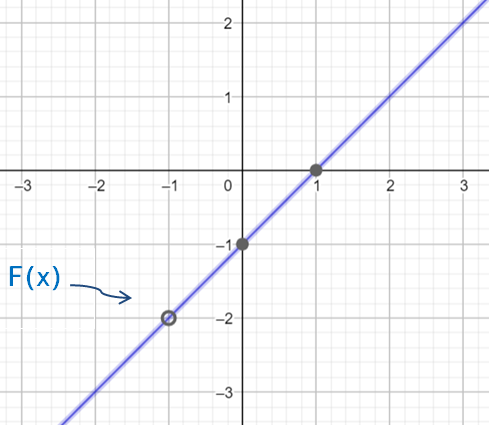
أجد قيمة كل نهاية ممّا يأتي (إن وُجدت) بيانيًا وعدديًا :

$7) \lim_{x \to 2} (x + 3)$	$8) \lim_{x \to 1} (x^{2} - 1)$

$9) \underset{x \to 3}{l i m} f (x), f (x) = \{\begin{cases} 2 x, & x \geq 3 \\ x + 3, & x < 3 \end{cases}$	$10) \underset{x \to 1}{l i m} g (x), g (x) = \{\begin{cases} - x + 1, & x \leq - 1 \\ x - 1, & x > - 1 \end{cases}$

الحل :

7) \lim_{x \to 2} (x + 3)

كلما اقتربت قيم x من العدد 2 من جهة اليمين اقتربت قيم الاقتران من العدد 5 ، وكذلك كلما اقتربت قيم x من العدد 2 من جهة اليسار اقتربت قيم الاقتران من العدد 5 ، إذن :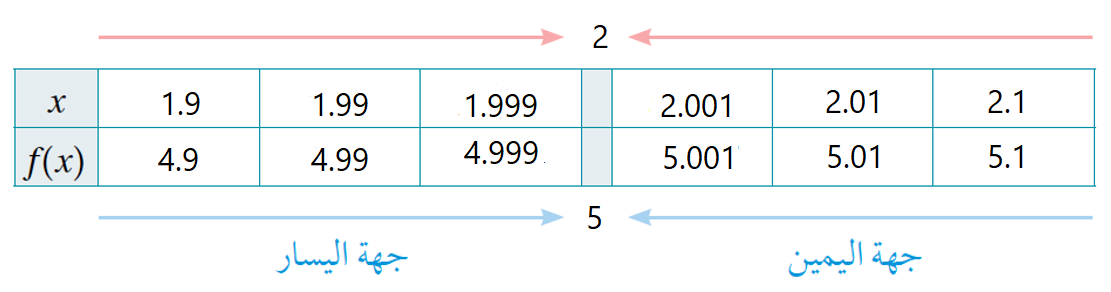

\lim_{x \to 2} (x + 3) = 5

أُلاحظ من التمثيل البياني المجاور أنّه كلما اقتربت قيم x من العدد 2 من جهة اليمين فإن قيم الاقتران تقترب من العدد 5 ، وهذا يعني أنّ :

$\lim_{x \to 2^{+}} (x + 3) = 5$

وكذلك : كلما اقتربت قيم x من العدد 2 من جهة اليسار اقتربت قيم الاقتران من العدد 5 ، وهذا يعني : $\lim_{x \to 2^{-}} (x + 3) = 5$

إذن : $\lim_{x \to 2} (x + 3) = 5$

8) \lim_{x \to 1} (x^{2} - 1)

كلما اقتربت قيم x من العدد 1 من جهتي اليمين واليسار تقترب قيم الاقتران من العدد 0 ، إذن :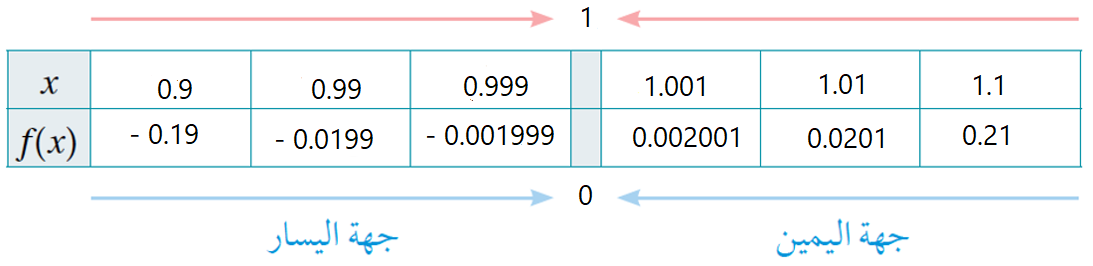

\lim_{x \to 1} (x^{2} - 1) = 0

أُلاحظ من التمثيل البياني المجاور أنّه كلما اقتربت قيم x من العدد 1 من جهة اليمين فإن قيم الاقتران تقترب من العدد 0 ، وهذا يعني أنّ :

$\lim_{x \leftarrow 1^{+}} (x^{2} - 1) = 0$

وكذلك : كلما اقتربت قيم x من العدد 1 من جهة اليسار اقتربت قيم الاقتران من العدد 0 ، وهذا يعني : $\lim_{x \to 1^{-}} (x^{2} - 1) = 0$ ، إذن :

$\lim_{x \to 1} (x^{2} - 1) = 0$

9) \underset{x \to 3}{l i m} f (x), f (x) = {\begin{cases} 2 x, & x \geq 3 \\ x + 3, & x < 3 \end{cases}

كلما اقتربت قيم x من العدد 3 من جهتي اليمين واليسار تقترب قيم الاقتران من العدد 6 ، إذن :

\lim_{x \to 3} f (x) = 6

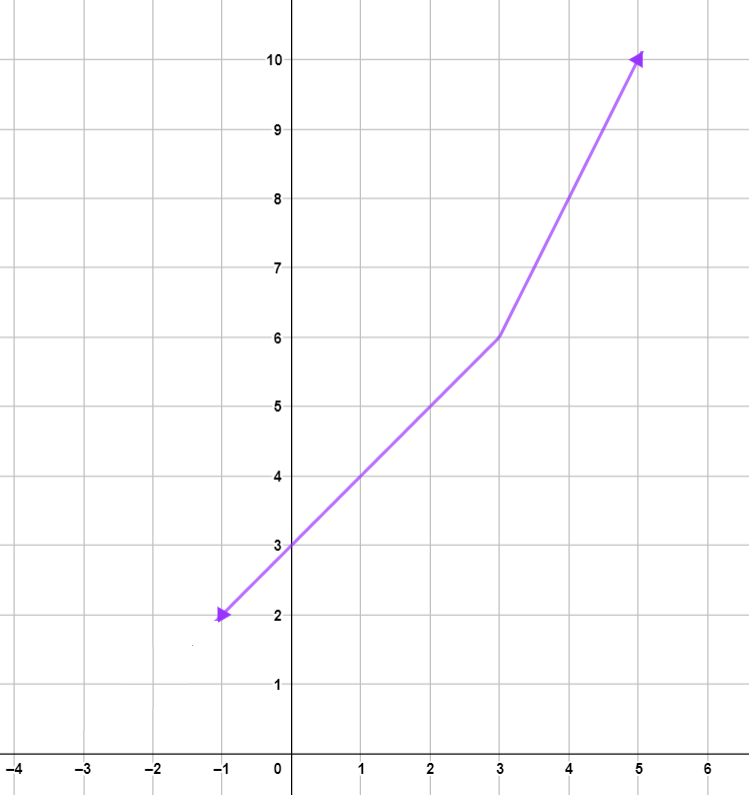
أُلاحظ من التمثيل البياني المجاور أنّه كلما اقتربت قيم x من العدد 3 من جهة اليمين فإن قيم الاقتران تقترب من العدد 6 ، وهذا يعني أنّ :

$\lim_{x \to 3^{+}} f (x) = 6$

وكذلك : كلما اقتربت قيم x من العدد 3 من جهة اليسار اقتربت قيم الاقتران من العدد 6 ، وهذا يعني :

$\lim_{x \to 3^{-}} f (x) = 6$

إذن : $\lim_{x \to 3} f (x) = 6$

10) \underset{x \to - 1}{l i m} g (x), g (x) = {\begin{cases} - x + 1, & x \leq - 1 \\ x - 1, & x > - 1 \end{cases}

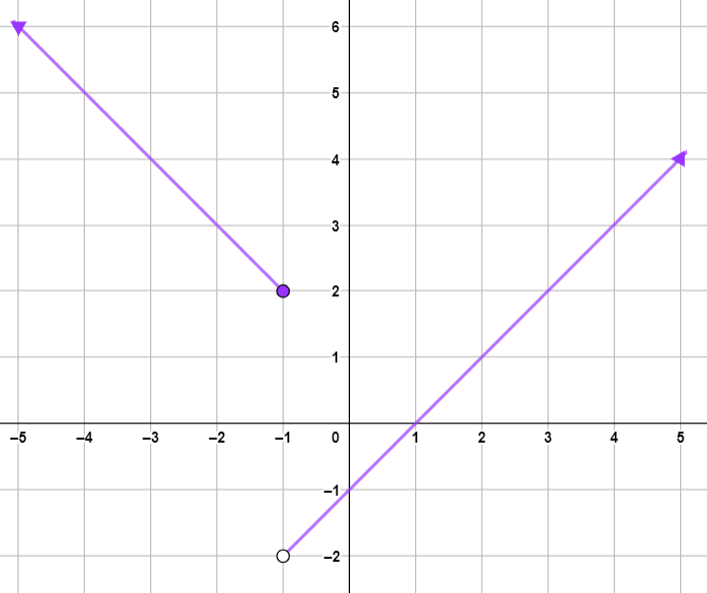
كلما اقتربت قيم x من العدد 1- من جهة اليمين ، اقتربت قيم الاقتران من العدد 2-

وهذا يعني أنّ : $\lim_{x \to - 1^{+}} g (x) = - 2$

وكلما اقتربت قيم x من العدد 1- من جهة اليسار ، اقتربت قيم الاقتران من العدد 2

وهذا يعني أنّ : $\lim_{x \to - 1^{-}} g (x) = 2$ ، وبما أنّ $\lim_{x \to - 1^{+}} g (x) \neq \lim_{x \to - 1^{-}} g (x)$ ، فإنّ : $\lim_{x \to - 1} g (x)$ غير موجودة .

أُلاحظ من التمثيل البياني المجاور أنّه كلما اقتربت قيم x من العدد 1- من جهة اليمين فإن قيم الاقتران تقترب من العدد 2- ، وهذا يعني أنّ : $\lim_{x \to - 1^{+}} g (x) = - 2$

وكذلك : كلما اقتربت قيم x من العدد 1- من جهة اليسار اقتربت قيم الاقتران من العدد 2 ، وهذا يعني : $\lim_{x \to - 1^{-}} g (x) = 2$ ، وبما أنّ : $\lim_{x \to - 1^{+}} g (x) \neq \lim_{x \to - 1^{-}} g (x)$

إذن : $\lim_{x \to - 1} g (x)$ غير موجودة.

أستعمل الخصائص الجبرية للنهايات لإيجاد قيمة كل نهاية ممّا يأتي :

13) \lim_{x \to 3} \sqrt[3]{\frac{2 x + 2}{x^{2} + 18}}

12) \lim_{x \to 4} (\sqrt{x} + \frac{4}{x})

11) \lim_{x \to - 1} (x^{2} + 2 x + 1)

الحل :

11) \lim_{x \to - 1} (x^{2} + 2 x + 1) = \lim_{x \to - 1} (x^{2}) + \lim_{x \to - 1} (2 x) + \lim_{x \to - 1} 1 = {(\lim_{x \to - 1} x)}^{2} + 2 \times \lim_{x \to - 1} x + \lim_{x \to - 1} 1 = {(- 1)}^{2} + 2 (- 1) + 1 = 0

12) \lim_{x \to 4} (\sqrt{x} + \frac{4}{x}) = \lim_{x \to 4} \sqrt{x} + \lim_{x \to 4} \frac{4}{x} = \sqrt{\lim_{x \to 4} x} + \frac{\lim_{x \to 4} 4}{\lim_{x \to 4} x} = \sqrt{4} + \frac{4}{4} = 3

13) \lim_{x \to 3} \sqrt[3]{\frac{2 x + 2}{x^{2} + 18}} = \sqrt[3]{\lim_{x \to 3} (\frac{2 x + 2}{x^{2} + 18})} = \sqrt[3]{\frac{\lim_{x \to 3} 2 x + 2}{\lim_{x \to 3} x^{2} + 18}} = \sqrt[3]{\frac{\lim_{x \to 3} 2 x + \lim_{x \to 3} 2}{\lim_{x \to 3} x^{2} + \lim_{x \to 3} 18}} = \sqrt[3]{\frac{2 \times \lim_{x \to 3} x + \lim_{x \to 3} 2}{{(\lim_{x \to 3} x)}^{2} + \lim_{x \to 3} 18}} = \sqrt[3]{\frac{2 \times 3 + 2}{3^{2} + 18}} = \sqrt[3]{\frac{8}{27}} = \frac{2}{3}

أجد قيمة كل نهاية ممّا يأتي (إنْ وُجِدت):

14) \lim_{x \to 1} \frac{x^{2} - 2 x + 1}{x - 1}

15) \lim_{x \to 1} \frac{x^{3} - x}{x - 1}

16) \underset{x \to 2}{l i m} \frac{x^{2} - 5 x + 6}{x^{2} - 4}

الحل:

14) \underset{x \to 1}{l i m} \frac{x^{2} - 2 x + 1}{x - 1} = \lim_{x \to 1} \frac{(x - 1) (x - 1)}{x - 1} = \lim_{x \to 1} (x - 1) = 0

15) \underset{x \to 1}{l i m} \frac{x^{3} - x}{x - 1} = \lim_{x \to 1} \frac{x (x^{2} - 1)}{x - 1} = \lim_{x \to 1} \frac{x (x - 1) (x + 1)}{x - 1} = \lim_{x \to 1} x (x + 1) = 1 (1 + 1) = 2

16) \lim_{x \to 2} \frac{x^{2} - 5 x + 6}{x^{2} - 4} = \lim_{x \to 2} \frac{(x - 2) (x - 3)}{(x - 2) (x + 2)} = \lim_{x \to 2} \frac{x - 3}{x + 2} = \frac{2 - 3}{2 + 2} = \frac{- 1}{4}

أبحث اتصال كل من الاقترانات الآتية عند قيمة x المعطاة إزاء كل منها:

$17) f (x) = \{\begin{cases} 2 x, & x < 2 \\ x^{2}, & x \geq 2 \end{cases}, x = 2$	$18) f (x) = \{\begin{cases} 2 x + 1, & x < - 1 \\ x^{3}, & x \geq - 1 \end{cases}, x = - 1$
$19) f (x) = x^{2} + 2 x + 3, x = 0$	$20) h (x) = \frac{x^{3} + 8}{2}, x = 2$
$21) g (x) = \frac{x^{2} + 3 x + 2}{x + 2}, x = - 2$	$22) q (x) = \frac{3 x^{2} + x}{x}, x = 0$

الحل :

$17) f (x) = {\begin{cases} 2 x, & x < 2 \\ x^{2}, & x \geq 2 \end{cases}, x = 2 f (2) = {(2)}^{2} = 4 \lim_{x \to 2^{+}} f (x) = \lim_{x \to 2^{+}} x^{2} = 4 \lim_{x \to 2^{-}} f (x) = \lim_{\to \infty} 2 x = 4$	بما أنّ : $f (2) = \lim_{x \to 2} f (x)$ إذن الاقتران f(x) متصل عند x = 2
$18) f (x) = {\begin{cases} 2 x + 1, & x < - 1 \\ x^{3}, & x \geq - 1 \end{cases}, x = - 1 f (- 1) = {(- 1)}^{3} = - 1 \underset{x \to - 1^{+}}{l i m} f (x) = \underset{x \to - 1^{+}}{l i m (x^{3}) = {(- 1)}^{3}} = - 1 \underset{x \to - 1^{-}}{l i m} f (x) = \underset{x \to - 1^{-}}{l i m} (2 x + 1) = 2 (- 1) + 1 = - 1$	بما أنّ: $f (- 1) = \lim_{x \to - 1} f (x)$ إذن الاقتران f متصل عند x = -1

$19) f (x) = x^{2} + 2 x + 3, x = 0 f (0) = 0^{2} + 2 (0) + 3 = 3 \underset{x \to 0}{l i m} f (x) = \underset{x \to 0}{l i m} (x^{2} + 2 x + 3) = 3$	بما أنّ: $f (0) = \lim_{x \to 0} f (x)$ إذن الاقتران f متصل عند x = 0

$20) h (x) = \frac{x^{3} + 8}{2}, x = 2 h (2) = \frac{2^{3} + 8}{2} = \frac{16}{2} = 8 \underset{x \to 2}{l i m} h (x) = \underset{x \to 2}{l i m} \frac{x^{3} + 8}{2} = \frac{2^{3} + 8}{2} = 8$	بما أنّ: $h (2) = \lim_{x \to 2} h (x)$ إذن الاقتران f متصل عند x = 0

$21) g (x) = \frac{x^{2} + 3 x + 2}{x + 2}, x = - 2$	بما أنّ الاقتران g غير مُعرف عند x = -2 ، إذن الاقتران g غير متصل عند x = -2

$22) q (x) = \frac{3 x^{2} + x}{x}, x = 0$	بما أنّ الاقتران q غير مُعرف عند x = 0 ، إذن الاقتران q غير متصل عند x = 0

عمل: تعمل سميرة في محل لبيع الحُلِيِّ والجواهر لقاء راتب شهري وعمولة إضافية تعتمد على قيمة مبيعاتها الشهرية. يُمكِن تمثيل المبلغ الذي تحصل عليه سميرة شهريًّا بالاقتران الآتي ، حيث x قيمة مبيعاتها الشهرية بالدينار:

$p (x) = \{\begin{cases} 500 + 0.1 x, 0 \leq x \leq 8000 \\ 660 + 0.08 x, x > 8000 \end{cases}$

23) أجد راتب سميرة في شهر حزيران إذا كانت مبيعاتها فيه .JD 8000

الحل :

تعويض x = 8000 في القاعدة الأولى للاقتران

p (8000) = 5 00 + 0.1 (8000) = 1300

24) أُبيِّن أنَّ الاقتران p متصل عندما $x = 8000$ .

الحل :

بما أنّ : $p (8000) = \lim_{x \to 8000} p (x)$

إذن الاقتران p(x) متصل عند x = 8000

$p (x) = {\begin{cases} 500 + 0.1 x, 0 \leq x \leq 8000 \\ 660 + 0.08 x, x > 8000 \end{cases}$

$p (8000) = 500 + 0.1 (8000) = 1300 \lim_{x \to 8000^{+}} p (x) = \lim_{x \to 8000^{+}} (660 + 0.08 x) = 660 + 0.08 (8000) = 1300 \lim_{x \to 8000^{-}} p (x) = \lim_{x \to 8000^{-}} (500 + 0.1 x) = 550 + 0.1 (8000) = 1300$

25) ابحث اتصال الاقتران: $f (x) = \{\begin{cases} x^{2} - 1, x < - 1 \\ x^{3} + 1, x > - 1 \end{cases}$ عندما $x = - 1$ .

الحل :

الاقتران f(x) غير مُعرف عند x = - 1 ، إذن f(x) غير متصل عند x = - 1

f (x) = {\begin{cases} x^{2} - 1, x < - 1 \\ x^{3} + 1, x > - 1 \end{cases}, x = - 1

حلول أسئلة مهارات التفكير العليا

26) مسألة مفتوحة : أكتب اقترانًا نسبيًا f(x) ، بحيث يكونf(-1) غير مُعرَف ، وتكون $\lim_{x \to - 1} f (x) = - 2$ ، مبررًا إجابتي بيانيًا.

الحل

الاقتران f(x) غير مُعرف عند x = - 1

$f (x) = \frac{x^{2} - 1}{x + 1}$

$\lim_{x \to - 1} f (x) = \lim_{x \to - 1} \frac{x^{2} - 1}{x + 1}$

$= \lim_{x \to - 1} \frac{(x - 1) (x + 1)}{x + 1}$

$= \lim_{x \to - 1} (x - 1) = - 1 - 1 = - 2$

27) تبرير : إذا كان : $f (x) = \{\begin{cases} x + 3, & x < 3 \\ 2 + \sqrt{k}, & x > 3 \end{cases}$ ، وكانت $\lim_{x \to 3} f (x)$ موجودة ، فأجد قيمة الثابت k ، مُبررًا إجابتي .

الحل :

بما أنّ النهاية موجودة ، إذن نهاية الاقتران من جهة اليمين تساوي نهاية الاقتران من جهة اليسار .

بالتعويض بقيمة x = 3 ، وحل المعادلة الناتجة فإنّ قيمة k = 16

\lim_{x \to 3^{+}} f (x) = \lim_{x \to 3^{-}} f (x) \lim_{x \to 3^{+}} (2 + \sqrt{k}) = \lim_{x \to 3^{-}} (x + 3) 2 + \sqrt{k} = 6 \sqrt{k} = 4 {(\sqrt{k})}^{2} = {(4)}^{2} k = 16

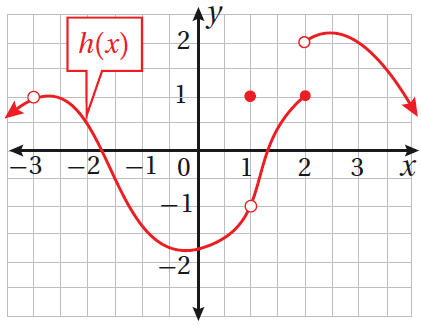
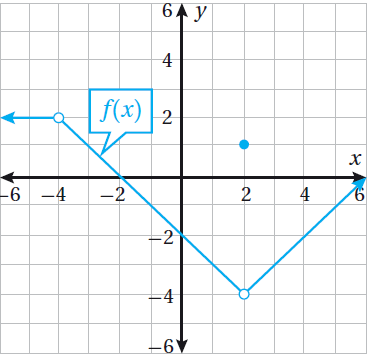
28) تبرير : أبيّن الفرق بين عدم اتصال الاقتران f المُمثّل بيانيًا في الشكل

المجاور عندما x = 2 ، وعدم اتصاله عندما x = - 4 ، مُبررًا إجابتي .الحل:

عند x = 2 ، الاقتران مُعرف عند x = 2 ولكنه غير متصل عند x = 2 لأن :

$\lim_{x \to 2} f (x) \neq f (2)$

إنما عند x = - 4 ، فالاقتران غير مُعرف عند x = - 4 ، لذا فهو غير متصل عند x = - 4

29) تحدِّ : إذا كان الاقتران : $h (x) = \{\begin{cases} x + 3, & x \neq 3 \\ x^{2} + k, & x = 3 \end{cases}$ متصلًا عندما x = 3 ، فأجد فيمة الثابت k.

الحل :

بما أنّ الاقتران h متصل عندما x = 3 ، إذن نهاية الاقتران

عند x = 3 تساوي قيمة الاقتران عند x = 3 ، بالتعويض وحل المعادلة الناتجة ، فإن k = - 3

$\lim_{x \to 3} h (x) = h (3) \lim_{x \to 3} (x + 3) = {(3)}^{2} + k 6 = 9 + k \to k = - 3$

حلول أسئلة كتاب التمارين

أجد قيمة كل نهاية ممّا يأتي (إنْ وُجِدت) اعتمادًا على التمثيل البياني المعطى:

1) \underset{x \to - 2}{l i m} h (x) 2) \lim_{x \to - 1} h (x) 3) \underset{x \to 1}{l i m} h (x)

الحل :

3) \lim_{x \to 1} h (x) = 3

2) \lim_{x \to - 1} h (x) = 3

1) \lim_{x \to - 2} h (x)

غير موجودة

أجد قيمة كل نهاية مما يأتي (إن وُجِدت) بالطريقتين البيانية والعددية :

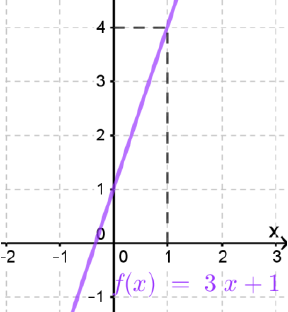
5) \underset{x \to 0}{l i m} h (x), h (x) = \{\begin{cases} x - 2, & - 2 \leq x < 0 \\ x - 1, & x \geq 0 \end{cases}

4) \underset{x \to 1}{l i m} (3 x + 1)

الحل :

$4) \underset{x \to 1}{l i m} (3 x + 1)$

بيانيًا : من الرسم المجاور يتبين أنّ :

$\lim_{x \to 1^{+}} h (x) = \lim_{x \to 1^{-}} h (x) = 4 \lim_{x \to 1} h (x) = 4$

عدديًا : ألاحظ أنه كلما اقتربت قيم x من جهني اليمين واليسار من العدد 1 تقترب قيم الاقتران من العدد 4 ، أي :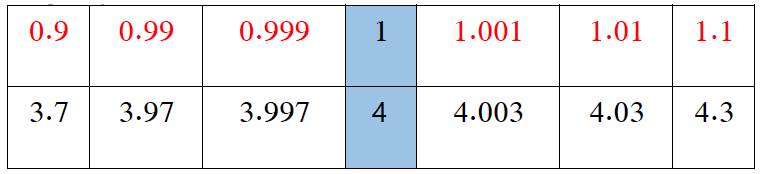

\lim_{x \to 1} h (x) = 4

$5) \underset{x \to 0}{l i m} h (x), h (x) = {\begin{cases} x - 2, & - 2 \leq x < 0 \\ x - 1, & x \geq 0 \end{cases}$

الحل :

بيانيًا : من الرسم المجاور يتبين أنّ :

$\lim_{x \to 0^{+}} h (x) = - 1$

$\lim_{x \to 0^{-}} h (x) = - 2$

وبما أن النهاية من جهة اليمين لا تساوي النهاية من جهة اليسار ، إذن : $\lim_{x \to 0} h (x)$ غير موجودة.

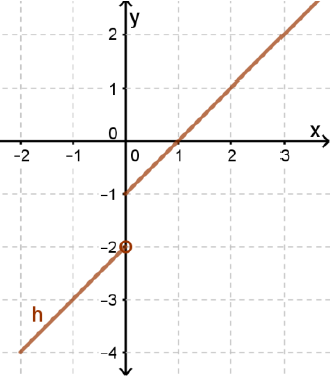عدديًا : ألاحظ من الجدول أنه كلما اقتربت قيم x من العدد 0 من جهة اليمين اقتربت قيم الاقتران h من العدد 2 - ، وكلما اقتربت قيم x من العدد 0 من جهة اليسار اقتربت قيم الاقتران h من العدد 1 - ، إذن :

\lim_{x \to 0} h (x)

غير موجودة.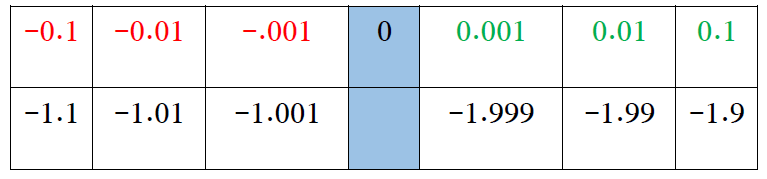

أستعمل الخصائص الجبرية للنهايات لإيجاد قيمة كل نهاية مما يأتي :

7) \underset{x \to 2}{l i m} \sqrt{2 x^{2} + 8}

6) \lim_{x \to 1} (3 x^{2} + x - 1)

الحل :

$6) \underset{x \to 1}{l i m} (3 x^{2} + x - 1) = \lim_{x \to 1} (3 x^{2}) + \underset{}{\lim_{x \to 1} (x) - \lim_{x \to 1} (1)} = 3 {(\lim_{x \to 1} x)}^{2} + \lim_{x \to 1} (x) - \lim_{x \to 1} (1) = 3 {(1)}^{2} + 1 - 1 = 3$

7) \underset{x \to 2}{l i m} \sqrt{2 x^{2} + 8} = \sqrt{\underset{x \to 2}{\lim (2 x^{2}} + 8)} = \sqrt{\lim_{x \to 2} (2 x^{2}) + \underset{x \to 2}{\lim (8)}} = \sqrt{2 (\lim_{x \to 2} {(x)}^{2} + \lim_{x \to 2} (8)} = \sqrt{2 (\underset{x \to 2}{\lim x)^{2}} + \lim_{x \to 2} (8)} = \sqrt{2 {(2)}^{2} + 8} = \sqrt{16} = 4

أجد قيمة كل نهاية ممّا يأتي (إن وُجدت) :

10) \underset{x \to 1}{l i m} \frac{x^{3} - x^{2}}{x^{2} - 1}

9) \underset{x \to - 1}{l i m} \frac{x^{2} + 2 x + 1}{x + 1}

8) \underset{x \to 4}{l i m} \frac{5 x - 20}{x - 4}

الحل :

10) \underset{x \to 1}{l i m} \frac{x^{3} - x^{2}}{x^{2} - 1} = \lim_{x \to 1} \frac{x^{2} (x - 1)}{(x - 1) (x + 1)} = \lim_{x \to 1} \frac{x^{2}}{x + 1} = \frac{1}{2}

9) \underset{x \to - 1}{l i m} \frac{x^{2} + 2 x + 1}{x + 1} = \lim_{x \to - 1} \frac{(x + 1) (x + 1)}{x + 1} = \lim_{x \to - 1} (x + 1) = 0

8) \underset{x \to 4}{l i m} \frac{5 x - 20}{x - 4} = \lim_{x \to 4} \frac{5 (x - 4)}{x - 4} = \lim_{x \to 4} 5 = 5

أبحث اتصال كل اقتران مما يأتي عند قيمة x المعطاة إزاءه :

$12) g (x) = \{\begin{cases} 3 x, & x < 1 \\ 4 x - 1, & x > 1 \end{cases}, x = 1$	$11) f (x) = \{\begin{cases} 2 x^{2}, & x < 1 \\ x + 1 & x \geq 1 \end{cases}, x = 1$

$14) q (x) = \{\begin{cases} \frac{8 - x^{3}}{x - 2}, & x \neq 2 \\ - 12, & x = 2 \end{cases}, x = 2$	$13) h (x) = {\begin{cases} 2 x, & x = - 2 \\ x + 2, & x \neq - 2 \end{cases}, x = - 2$

الحل :

بما أنّ : $f (1) = \lim_{x \to 1} f (x)$ ، إذن الاقتران f(x) متصل عند x = 1	$11) f (x) = {\begin{cases} 2 x^{2}, & x < 1 \\ x + 1 & x \geq 1 \end{cases}, x = 1 f (1) = 1 + 1 = 2 \underset{x \to 1^{+}}{l i m} f (x) = \underset{x \to 1^{+}}{l i m} (x + 1) = 1 + 1 = 2 \underset{x \to 1^{-}}{l i m} f (x) = \underset{x \to 1^{-}}{l i m} (2 x^{2}) = 2 {(1)}^{2} = 2$

الاقتران g(x) غير معرف عند x = 1 ، لذا هو غير متصل عند x = 1	$12) g (x) = {\begin{cases} 3 x, & x < 1 \\ 4 x - 1, & x > 1 \end{cases}, x = 1$

الاقتران h(x) غير متصل عند x = - 2 ، لأن : $h (- 2) \neq \lim_{x \to - 2} h (x)$	$13) h (x) = {\begin{cases} 2 x, & x = - 2 \\ x + 2, & x \neq - 2 \end{cases}, x = - 2 h (- 2) = 2 \times - 2 = - 4 \underset{x \to - 2}{l i m} h (x) = - 2 + 2 = 0$

بما أنّ : $q (2) = \lim_{x \to 2} q (x)$ فالاقتران q(x) متصل عند x = 2	$14) q (x) = {\begin{cases} \frac{8 - x^{3}}{x - 2}, & x \neq 2 \\ - 12, & x = 2 \end{cases}, x = 2 q (2) = - 12 \underset{x \to 2}{l i m} q (x) = \underset{x \to 2}{l i m} \frac{8 - x^{3}}{x - 2} = \underset{x \to 2}{l i m} \frac{\overset{- 1}{(2 - x)} (4 + 2 x + x^{2})}{x - 2} = \underset{x \to 2}{l i m} - 1 (4 + 2 x + x^{2}) = - 12$

رياضيات أدبي فصل ثاني

الأول ثانوي أدبي

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS