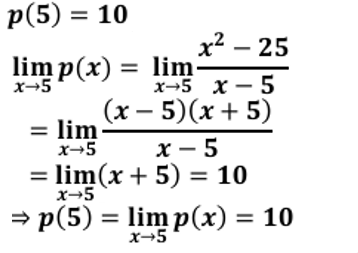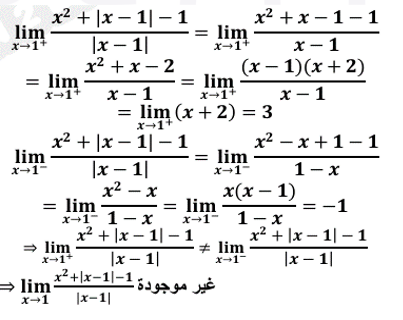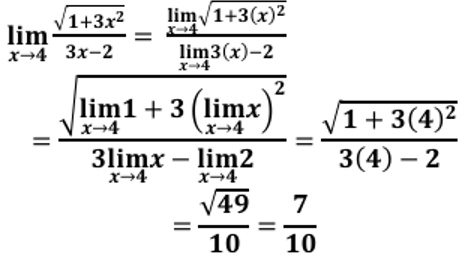النهايات والاتصال
أتحقق من فهمي صفحة 54
أجد كلًًّّا من النهايات الآتية بيانيًّا وعدديًّا:
|
|
الحل:
|
a) عدديا
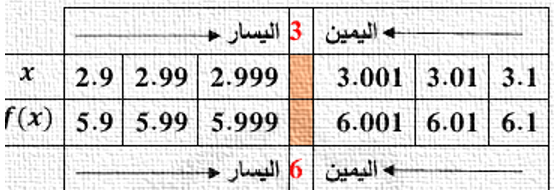
|
بيانيا
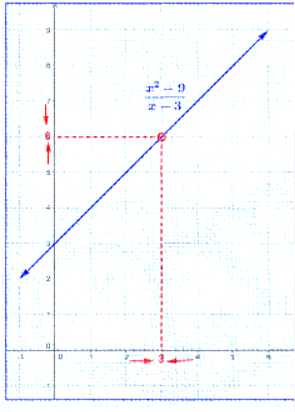
|
|
b) عدديا
|
بيانيا
|
أتحقق من فهمي صفحة 56
أجد كلًًّّا من النهايات الآتية بيانيًّا:
|
|
الحل:
|
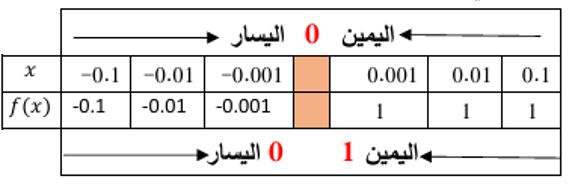
a)
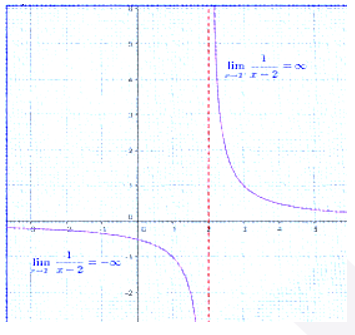
|
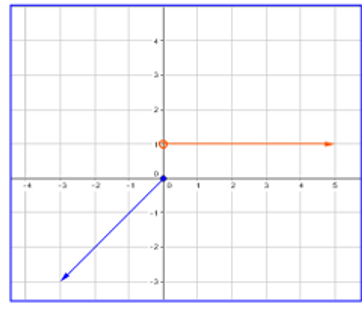
b)
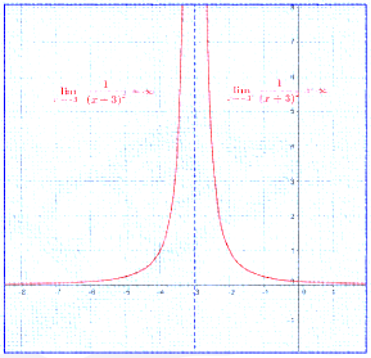
|
أتحقق من فهمي صفحة 58
أستعملُ خصائص النهايات لحساب كلّ نهاية ممّا يأتي:
|
|
الحل:
|
a)
|
|
b)
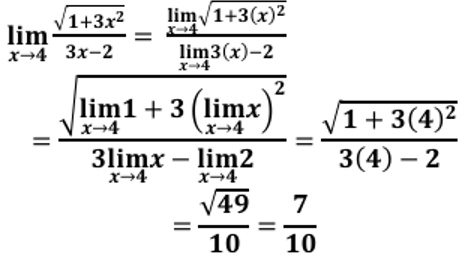
|
أتحقق من فهمي صفحة 59
أجد كلّ نهاية ممّا يأتي باستعمال التعويض المباشر إذا كان ممكنًا، وإلّّا فأذكرُ السبب:
|
|
|
|
الحل:

أتحقق من فهمي صفحة 61
أجد كلّ نهاية ممّا يأتي:
|
|
|
الحل:
| a) |
|
| b) |
c) |
أتحقق من فهمي صفحة 64
أُحدّد إذا كان كلّ اقتران ممّا يأتي متّصلًًا عند قيمة x المعطاة، وأبرّر إجابتي:
|
|
|
|
الحل:
a) الاقتران متصل عند x=1 لأن .
b) الاقتران غير متصل عند x=5 لأن الاقتران غير معرف عند x=5
c)
إذن الاقتران متصل عند x=3.
d)
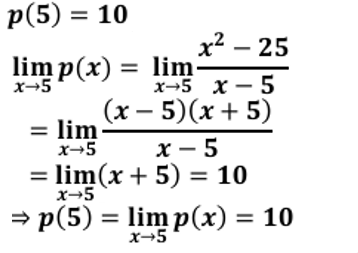
أتدرّب وأحلّ المسائل (صفحة 64)
أجد كلا من النهايات الآتية بيانيًّا وعدديًّا:
|
|
|
|
|
|
|
|
الحل:
|
1)
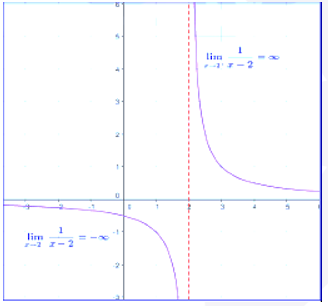
|
2)
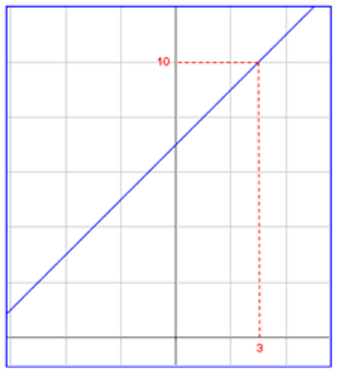
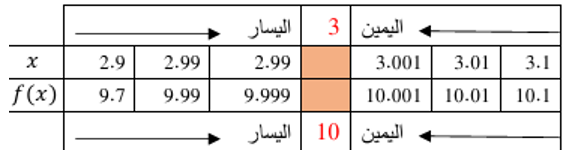
|
|
3)
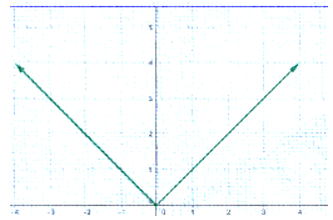
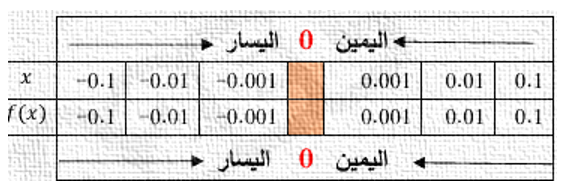
|
4)
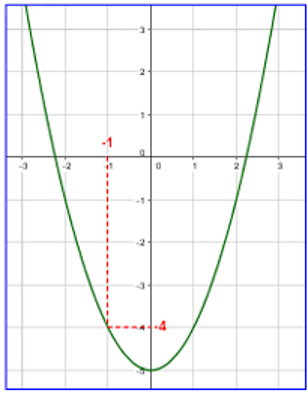
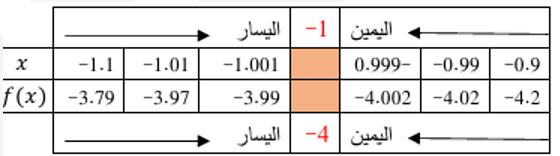
|
|
5)
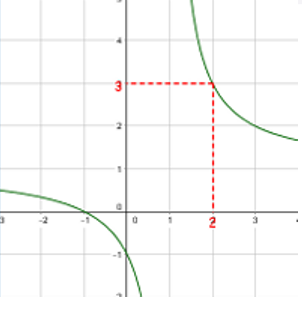
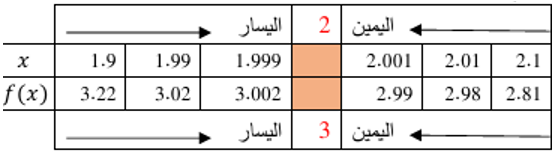
|
6)
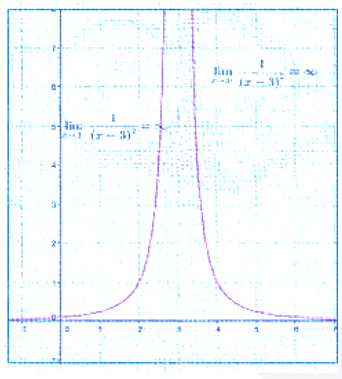
|
|
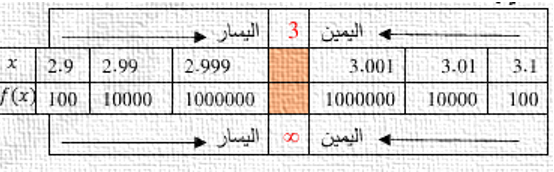
7)
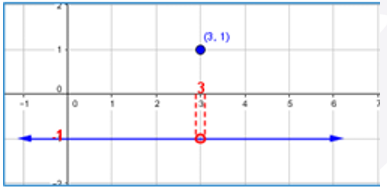
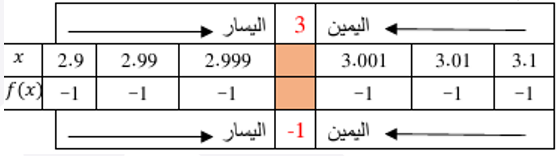
|
8)
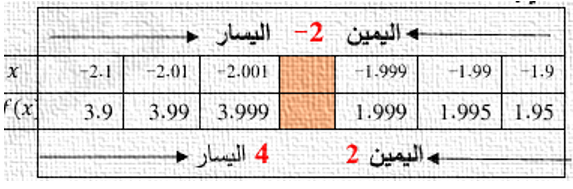
|
أجد كلّ نهاية ممّا يأتي:
|
|
|
|
|
|
|
|
|
|
|
|
الحل:
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
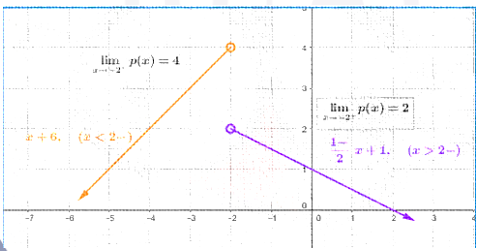
أستعملُ التمثيل البياني؛ لأجد كلّ نهاية ممّا يأتي:
 |
|
|
الحل:
21) 4
22) غير موجودة
أستعملُ التمثيل البياني؛ لأجد كلّ نهاية ممّا يأتي:
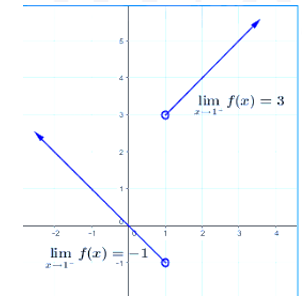
| |
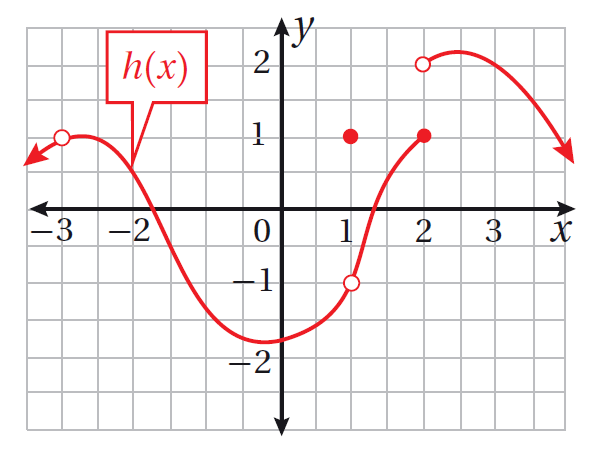 |
| |
|
الحل:
23)
24) غير موجودة
25)
26) إذا كان ، حيثُ ، وكان ، ، ؛ فأجد قيم الثوابت a و b و c.
الحل:
بما أن الاقتران كثير حدود فإنّ:
|
|
بح حل نظام المعادلات الخطية الناتج بالحذف او التعويض نجد أنّ:
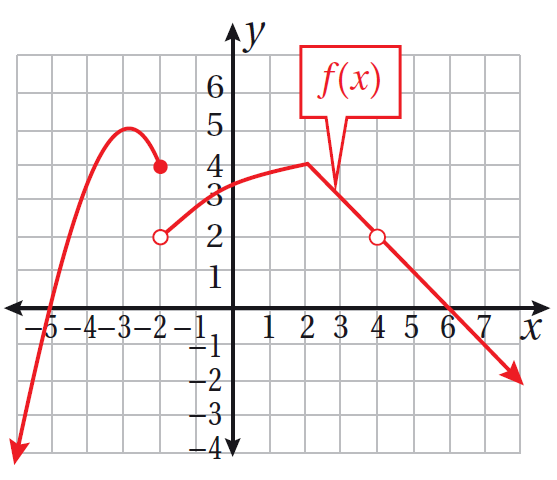
أستعملُ التمثيلين البيانيين المجاورين؛ لأجد كلّ نهاية ممّا يأتي:
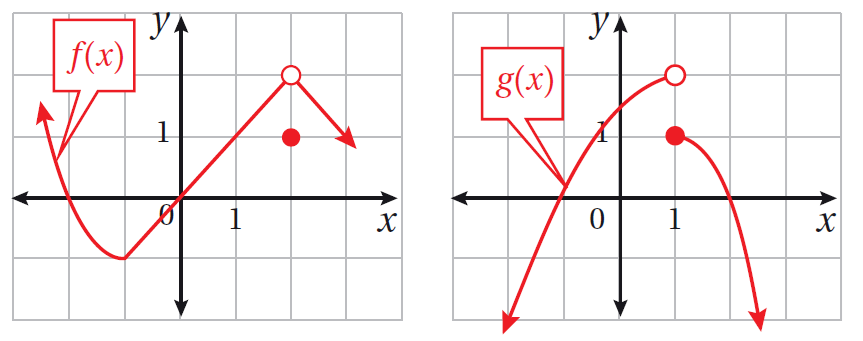
|
|
|
الحل:
| 27) |
| 28) |
| 29) |
أُحدّد إذا كان كلّ اقتران ممّا يأتي متّصلًًا عند قيمة x المعطاة، وأبرّر إجابتي:
|
|
|
الحل:
30) متصل لأنه كثير حدود
31) متصل لأن الاقتران نسبي معرف عند
32)
غير موجودة
إذن الاقتران غير متصل عند
33) إذا كان متّصلًًا عند x = 3 ؛ فأجد قيمة الثابت
الحل:
الاقتران متصل عند ، إذن:
مهارات التفكير العليا
34) تحدّ: أجد بيانيًّا وجبريًّا.
الحل:
35) تبرير: أجد قيمتَي الثابتين m و b اللتين تجعلان ، وأبرّر إجابتي.
الحل:
بما أن المقام صفر والنهاية موجودة اذن البسط صفر
36) تبرير: أجد قيمة الثابت a التي تجعل موجودة، وأبرّر إجابتي.
الحل:
بتحليل البسط :
بما أن المقام عند x=1 صفر والنهاية موجودة اذن البسط عند x=1 يجب أن يكون صفر