رياضيات فصل ثاني

فِكرةُ الدّرس

•أَتعرَّفُ النِّسبةَ، وَأَكتُبها بِصُوَرٍ مُخْتَلفة.
•أَجِدُ المُعَدَّلَ، وَمُعَدَّلَ الْوَحْدَةِ.

 

الْمُصْطَلَحاتُ:

النِّسبَةُ، المُعَدَّلُ، مُعَدَّلُ الْوَحْدَةِ.
 

النِّسبَةُ هِيَ طَريقَةٌ لِمُقارَنةِ عدَدٍ مَعَ آخَرَ أَوْ كَمّيَّة معَ أُخْرى. وَتُكتبُ النِّسبَةُ بِثَلاث طَرائِقَ؛ فَمثَلًا يُمكِنُ كِتابَةُ نِسبَةِ الأزْرارِ الحَمراءِ إِلى الزَّرقاءِ في الشَّكْلِ الْمُجاوِرِ عَلى النَّحْوِ الآتي: $3 : 2 \frac{3}{2} 2 \mathrm{إلى} 3$ وَيُمكِنُ تَبسيطُ النِّسبَةِ كَما في الكُسورِ بِقِسمَةِ طَرَفَيها عَلى العامِلِ المُشْتَرَكِ الأكْبَرِ بَينَهُما.

 

 

 

 

 

 

 

مثال

اعْتِمادًا عَلى الشَّكلِ المُجاورِ، أَكْتُبُ في أَبْسَطِ صورَةٍ:                                        1) نِسْبَةَ الْمُرَبَّعاتِ إِلى الْمُثَلَّثاتِ. 2) نِسْبَةَ الدَّوائِرِ إِلى الْمُرَبَّعاتِ. 3) نِسْبَةَ الْمُثَلَّثاتِ إِلى الدَّوائِرِ . 4) نِسْبَةَ الْمُثَلَّثاتِ إِلى الْمُرَبَّعاتِ إِلى الدَّوائِرِ .

 

 

 

 

 

 

 

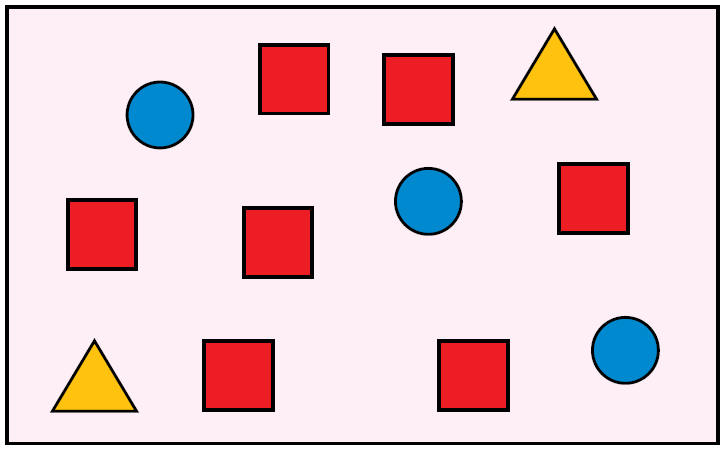الجواب:

أَكْتُبُ النِّسْبَةَ بَيْنَ الْكَمِّيَّات حَسَبَ تَرْتيبِ وُرودِهِم في نَصِّ السُّؤالِ بَدْءًا مِنَ الْيَسارِ.

1) توجَدُ 7 مُرَبَّعاتٍ وَمُثَلَّثٌان.

$\mathbf{7} : \mathbf{2}$

2) توجَدُ 3 دَّوائِرِ و 7 مُرَبَّعاتٍ.

$\mathbf{3} : \mathbf{7}$

3) يوجَدُ مُثَلَّثٌان و 3 دَّوائِرِ .

$\mathbf{2} : \mathbf{3}$

4) يوجَدُ مُثَلَّثٌان و 7 مُرَبَّعاتٍ و 3 دَّوائِرِ.

$\mathbf{2} : \mathbf{7} : \mathbf{3}$

---

وأحيانا نقوم بتَبسيطُ النِّسبَةِ كَما في الكُسورِ إذا كان هناك عامِلِ مُشْتَرَكِ أكْبَرِ بَينَهُما.

مثال

اعْتِمادًا عَلى الشَّكلِ المُجاورِ، أَكْتُبُ في أَبْسَطِ صورَةٍ نِسْبَةَ الأزرار الزرقاء إِلى الأزرار الحمراء. الجواب النسبة هي: $\mathbf{6}\mathbf{ }\mathbf{:}\mathbf{ }\mathbf{4}$ وهنا نبَسِّطُ النِّسْبَةِ بِالْقِسْمَةِ عَلى الْعامِلِ الْمُشْتَرَكِ الأكْبَرِ وهُوَ 2 . $\mathbf{6} ÷2 : \mathbf{4} ÷2 \to \mathbf{3} : \mathbf{2}$ إذن؛ نِسْبَةَ الأزرار الزرقاء إِلى الأزرار الحمراء هي: $\mathbf{3}\mathbf{ }\mathbf{:}\mathbf{ }\mathbf{2}$

 

 

 

 

 

 

 

 

تَتَطَلَّبُ كَثيرٌ مِنَ المَواقِفِ تَوزيعَ كَمِّيَّةٍ بَيْنَ عَدَدٍ مِنَ الأشْخاصِ وَفْقَ نِسبَةٍ مُحَدَّدَةٍ.

مثال

وزعت مُنى 160 JD  بَيْنَ أخواتها ريم وفاتن بِنِسْبَةِ 3 : 5، فَكَمْ أَخَذَت كُلٌّ مِنْهُما؟

الحل:

النِّسبَةُ 3 : 5 تَحْتَوي 8 أَجْزاءٍ مُتَساوِيَةٍ؛ لأنَّ 8 = 3 + 5

الخُطوَةُ 1: أَقْسِمُ الْعَدَدَ 160 عَلى 8؛ لأجِدَ قيمَةَ كُلِّ جُزْءٍ.

عدد الأجزاء

$\frac{160}{8}=20$

الخُطوَةُ 2: أُوزِّع الأجزاءَ الثمانية في مَجموعَتَيْنِ بِنِسْبَةِ 3 : 5، ثُمَّ أَجِدُ مَجْموعَ قِيَمِ الأجْزاءِ في كُلِّ مَجْموعَةٍ.

160
1 جُزْءًا	1 جُزْءًا	1 جُزْءًا	1 جُزْءًا	1 جُزْءًا	1 جُزْءًا	1 جُزْءًا	1 جُزْءًا
20	20	20	20	20	20	20	20
سَتحْصُلُ فاتن عَلى 3 أجزْاء $3 \times 20 = 60$			سَتحْصُلُ ريم على 5 أَجْزاءٍ  $5 \times 20 = 100$

يجب الانتباه أن ريم ستكون لها 5 أجزاء لأنها ذُكرت أولا في السؤال، أما فاتن سيكون لها 3 أجزاء.

إِذَنْ، أَخَذَت ريم JD 100 ، وَأَخَذَت فاتن JD 60.

---

المُعَدلُ هُوَ نِسبَةٌ تُقارِنُ بَيْنَ كَمِّيَّتَيْنِ لَهُما وَحْدَتانِ مُخْتَلِفَتانِ. عِنْدَ تَبْسيطِ الْمُعَدَّلِ لِيُصْبِحَ مَقامُهُ وَحْدَةً واحِدَةً، فَإِنَّهُ يُسَمّى مُعَدلَ الوَحدةِ.

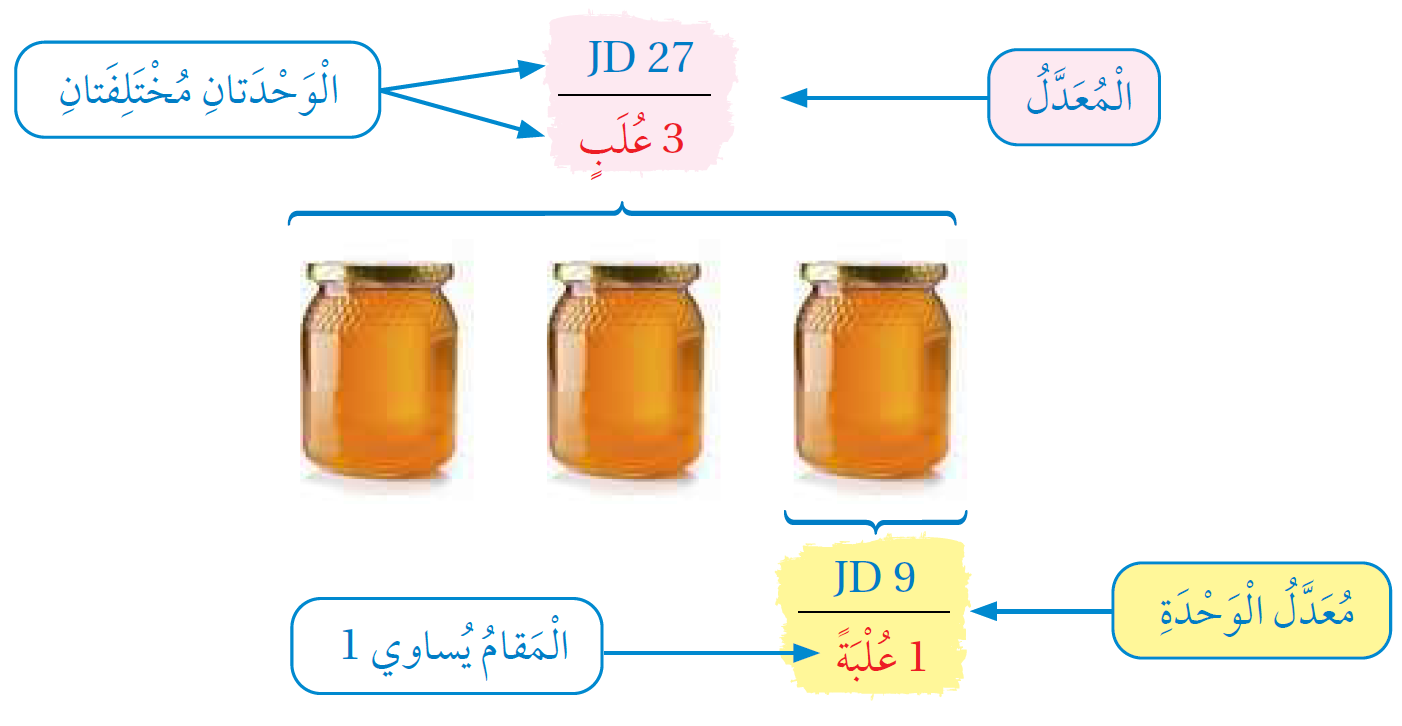
• ومن مُعدَّلات الوَحدَةِ الشّائعة في الحياةِ اليومِيَّةِ عَددُ الْكيلومِتراتِ المقطوعَةِ لِكُلِّ ساعةٍ$(km/h)$، وثَمنُ الْكيلوغِرام الواحدِ بِالدّينارِ $(JD/kg)$ 
• يُمكنُ حِسابُ مُعدَّل الوَحدةِ بِكتابَة المُعدَّل أَوّلا، ثُمَّ قِسْمَةِ كُلٍّ منَ البسطِ وَالمقام على المقام حَتّى يُصبِحَ المَقامُ مُساوِيًا الواحد.

 

مثال

أَكْتُبُ الْمُعَدَّلَ عَلى صورَةِ كَسْرٍ، ثُمَّ أَجِدُ مُعَدَّلَ الْوَحْدَةِ في كُلٍّ مِمّا يَأْتي:

1) تَقْطَعُ مَرْكَبَةٌ فَضائِيَّةٌ$112000 km$ في $5 h$ .

$\frac{112000 km}{5 h}$	أَكْتُبُ الْمُعَدَّلَ عَلى صورَةِ كَسر
$\frac{112000 km÷5}{5 h÷5}=\frac{22400 km}{1 h}$	أَجِدُ مُعَدَّلَ الْوَحْدَةِ: أَقْسِمُ الْبَسْطَ وَالْمَقامَ على 5؛ حَتّى يُصْبِحَ الْمَقامُ 1

إِذَنْ، مُعَدَّلُ الْوَحْدَةِ هُوَ $\frac{22400 km}{1 h}$ أَوْ $22400 km$ في السّاعَةِ الْواحِدَةِ.

 

2) تقطع سيارة$50 km$ في $2 h$.

أَكْتُبُ الْمُعَدَّلَ عَلى صورَةِ كَسر	$\frac{50 km}{2 h}$
أَجِدُ مُعَدَّلَ الْوَحْدَةِ: أَقْسِمُ الْبَسْطَ وَالْمَقامَ على 5؛ حَتّى يُصْبِحَ الْمَقامُ 1	$\frac{50 km÷2}{2 h÷2}=\frac{25 km}{1 h}$

 

إِذَنْ، مُعَدَّلُ الْوَحْدَةِ هُوَ $\frac{25 km}{1 h}$ أو $25 km$ في السّاعة الواحدة.

---

يُستَعملُ مُعدَّلُ الوَحدَةِ لمُقارنَة أَسعارِ السِّلعِ في العُروضِ التِّجارِيةِ المُختَلفَة.

مثال

أَيُّ العَرضَين الآتِيَين سعرُ الكُرسِيِّ الواحدِ فيه أَقَلُّ؟

الحل:

لإيجادِ سِعرِ الكُرسِيِّ الواحِدِ، أَحسبُ مُعدَّلَ الوَحدةِ.

الْعَرْضُ الأوَّلُ

أَكتُبُ المُعَدَّلَ عَلى صورَةِ كَسْرٍ. أُقارِنُ السِّعرَ الْكُلِّيَّ بِعَدَدِ الْكَراسي.

أَكتُبُ المُعَدَّل على صورَة كَسرٍ

$\frac{JD 88 }{\mathrm{كراسي} 4}$

أَجِدُ مُعَدَّلَ الوحدَةِ بِقِسمَةِ البَسطِ وَالمَقامِ عَلى 4

أَجِدُ مُعَدَّلَ الْوَحدَةِ: أَقسِمُ البسطَ وَالمَقامَ عَلى 4؛ حَتّى يُصبِح المَقامُ 1

$\frac{JD 88÷4}{ \mathrm{كراسي} 4÷4}=\frac{JD 22}{\mathrm{كرسيا} 1}$

إِذَن، مُعَدَّلُ الوَحدَةِ في العَرضِ الأوَّلِ 22 دينارًا لِكُلِّ كُرْسِيٍّ.

 

الْعَرْضُ الثّاني

أَكْتُبُ الْمُعدَّلَ عَلى صورَة كَسْرٍ. أُقارِنُ السِّعْرَ الْكُلِّيَّ بِعَدَدِ الْكَراسي.

أَكْتُبُ الْمُعَدَّلَ عَلى صورَةِ كَسْرٍ

$\frac{JD 228 }{\mathrm{كراسي} 12}$

أَجِدُ مُعَدَّلَ الْوَحْدَةِ بِقِسْمَةِ الْبَسْطِ وَالْمَقامِ عَلى 12

أَجِدُ مُعَدَّلَ الْوَحْدَةِ: أَقْسِمُ الْبَسْطَ وَالْمَقامَ عَلى 12؛ حَتّى يُصْبِحَ الْمَقامُ 1

$\frac{JD 228÷12}{ \mathrm{كراسي} 12÷12}=\frac{JD 19}{\mathrm{كرسيا} 1}$

إِذَنْ، مُعَدَّلُ الوَحدَةِ في العَرْضِ الثّاني 19 دينارًا لِكُلِّ كُرْسِيٍّ.

بِمُقارَنَةِ مُعَدَّلِ الوَحدَةِ في العَرضَيْنِ أُلاحِظُ أَنَّ سِعرَ الكُرسِيِّ الواحِد في العَرْضِ الثّاني أَقَلُّ.