رياضيات فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين

حلول أسئلة أتحقق من فهمي

أتحقق من فهمي صفحة 54

أَكْتُبُ نِسْبَةً تُكافِئُ النِّسْبَةِ المُوَضَّحَةِ في كُلٍّ مِمَّا يَأْتِي:

$\mathbf{3}\mathbf{)}\mathbf{ }14 : 10 \stackrel{÷2}{\to } 7 : 5$

$\mathbf{4}\mathbf{)} 5 : 7 \stackrel{\times 3}{\to } 15 : 21$

---

أتحقق من فهمي صفحة 55

أُكْمِلُ جَدْوَلَ النِّسْبَةِ في كُلٍّ مِمّا يَأْتي، ثُمَّ أَكْتُبُ النِّسَبَ الْمُتَكافِئَةَ:

3) 

18	6	عدد الدفاتر
39	13	عدد الأقلام

 

 

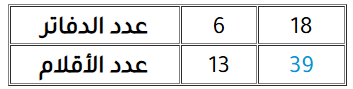
بمقارنة الأعمدة نُلاحظ أنّ عدد الدفاتر في العمود الثاني يُمثل عدد الأولاد في العمود الأول ضرب 3. أي أنّ: $6 \times 3 = 18$

إذن؛ عدد الأقلام في العمود الثاني؛ $13 \times 3 = 39$

 

4) 

147	21	3	عدد الأولاد
245	35	5	عدد البنات

 

 

بمقارنة الأعمدة نُلاحظ أنّ عدد الأولاد في العمود الثاني يُمثل عدد الأولاد في العمود الأول ضرب 7. أي أنّ: $3 \times 7 = 21$

إذن؛ عدد الأولاد في العمود الثالث؛ $21 \times 7 = 147$  ، وعدد البنات في العمود الثاني للصف الثاني؛ $5 \times 7 = 35$

---

أتحقق من فهمي صفحة 56

2) حَلْوَياتٌ: تَحْتَوي كُلُّ $200 g$ في طَبقٍَ مِنْ حَلاوَة الجُْبنِْ $14 g$ مِنَ السُّكَّرِ، ما كُتْلَةُ السُّكَّرِ الَّتي تَحْتَويها$300 g$ مِنَ الطبَّقَِ؟

الحل:

الْخُطْوَةُ 1: أُنْشِئُ جَدْوَلَ نِسْبَةٍ.

نِسْبَةُ عَدَدِ غرامات حلاوة الجبن إِلى عَدَدِ غرامات السكر هِيَ 14 : 200

وهنا أَكْتُبُ الْقِيَمَ الْمُعْطاةَ في جَدْوَلِ النِّسْبَةِ.

300		200	كتلة حلاوة الجبن (g)
		14	كتلة السكر (g)

 

 

الْخُطْوَةُ 2: أُكْمِلُ جَدْوَلَ النِّسْبَةِ.

لا يوجَدُ عَدَدٌ صَحيحٌ يُمْكِنُ ضَرْبُهُ في 200 لِلْحُصولِ عَلى 300 ؛ لِذا أُقَلِّصُ الْعَدَدَ 200 بِاسْتِعْمالِ الْقِسْمَةِ؛ لأحْصُلَ عَلى عَدَدٍ يُمْكِنُ ضَرْبُهُ في عَدَدٍ صَحيحٍ لِلْحُصولِ عَلى 300

وهنا أَقْسِمُ طَرَفَيِ النِّسْبَةِ الأولى عَلى 2

300	100	200	كتلة حلاوة الجبن (g)
	7	14	كتلة السكر (g)

 

 

 

بِما أَنَّ $100 \times 3 = 300$ ، إذن؛ أَضْرِبُ 7 في 3؛ لأحْصُلَ عَلى الْعَدَدِ الْمُقابِلِ في النِّسْبَةِ الثّالِثَةِ.

وهنا أَضْرِبُ طَرَفَيِ النِّسْبَةِ الثّانِيَةِ في 3

300	100	200	كتلة حلاوة الجبن (g)
21	7	14	كتلة السكر (g)

 

 

إِذَنْ، كُتْلَةُ كُتْلَةُ السُّكَّرِ الَّتي تَحْتَويها $300 g$ من الجبن تُساوي $21 g$

---

حلول أسئلة أتدرب وأحل المسائل

أَجِدُ نِسْبَةً تُكافِئُ كُلًّ مِنَ النِّسَبِ الآتِيَةِ:

1) 6 : 11                 12: 22                             ضرب طرفي النسبة بالعدد 2

2) 9 : 15                 3 : 5                      قسمة طرفي النسبة على العدد 3                           

  3) 21: 18              7: 6                         قسمة طرفي النسبة على العدد 3                          

  4) ضرب طرفي النسبة بالعدد2                         38 :26            19: 13   

 

أُكْمِلُ كُلَّ جَدْوَلِ نِسْبَةٍ مِمّا يَأْتي، ثُمَّ أَكْتُبُ النِّسَبَ الْمُتَكافِئَةَ:

5) 

8	2	عَدَدُ قَواريرِ الْماءِ
12	3	عَدَدُ اللِّتْراتِ

 

 

بِما أَنَّ $2 \times 4 = 8$، إذن؛ أَضْرِبُ 3 في 4 ؛ لأحْصُلَ عَلى الْعَدَدِ الْمُقابِلِ في النِّسْبَةِ الثانية. $3 \times 4 = 12$

النسب المُتكافئة:   $2 : 3 , 8 : 12$

6) 

1	2	عَدَدُ الْقِطَعِ
3	6	الثَّمَنُ بِالدّينارِ

 

 

بِما أَنَّ $6 ÷ 2 = 3$ ، إذن؛ يكون عدد الدفاتر في العمود الأول (2) حيثُ أن $2 ÷2 = 1$ 

النسب المُتكافئة:   $2 : 6 , 1 : 3$

7) 

100	20	240	عَدَدُ الْحَواسيبِ
15	3	36	عَدَدُ الطّابِعاتِ

 

 

بِما أَنَّ $240 ÷ 12 = 20$ ، إذن؛ أقسمُ 36 على 12 ؛ لأحْصُلَ عَلى الْعَدَدِ الْمُقابِلِ في النِّسْبَةِ الثانية. $36 ÷ 12 = 3$

وألاحظ أنّ في العمود الثالث العدد (15) جاء من ضرب (النسبة الثانية) العدد (3) في 5 حيثُ أنّ: $3 \times 5 = 15$

إذن؛ يكون عدد الحواسيب في العمود الأول (100) حيثُ أنّ: $20 \times 5 = 100$

النسب المُتكافئة:   $240 : 36 , 20 : 3 , 100 : 15$

8) 

40	10	5	عَدَدُ السَّيّاراتِ
32	8	4	عَدَدُ الْحافِلاتِ

 

 

بِما أَنَّ $5 \times 2 = 10$ ، إذن؛ أَضْرِبُ 4 في 2 ؛ لأحْصُلَ عَلى الْعَدَدِ الْمُقابِلِ في النِّسْبَةِ الثانية. $4 \times 2 = 8$

وألاحظ أنّ في العمود الثالث العدد (32) جاء من ضرب (النسبة الثانية) العدد (8) في 4 حيثُ أنّ: $8 \times 4 = 32$

إذن؛ يكون عدد السيارات في العمود الأول (40) حيثُ أنّ: $10 \times 4 = 40$

النسب المُتكافئة:   $5 : 4 , 10 : 8 , 40 : 32$

9) 

54	6	36	الطُّلابُ
99	11	66	الطّالِباتُ

 

 

 

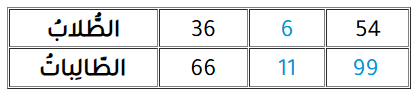
لا يوجد عدد صحيح يُمكن ضربهُ في 36 للحُصول على 54 ؛ لِذا أُقلّص العدد 36 بِاسْتِعمالِ الْقِسْمَةِ؛ لأحصلَ على عددٍ يُمكن ضربهُ في عَدد صحيحٍ للحُصول على 54

وهنا أَقْسمُ طرفيِ النّسبَةِ الأولى عَلى 6 ؛   $36 ÷ 6 = 6 , 66 ÷ 6 = 11$

بِما أَنَّ $6 \times 9 = 54$ ، إذن؛ أَضْرِبُ 11 في 9 ؛ لأحْصُلَ عَلى الْعَدَدِ الْمُقابِلِ في النِّسْبَةِ الثالثة. $11 \times 9 = 99$

النسب المُتكافئة:   $36 : 66 , 6 : 11 , 54 : 99$

10) 

200	20	100	عَدَدُ الْقُمْصانِ
70	7	35	عَدَدُ الْبَناطيلِ

 

 

 

هنا يوجد عدد صحيح يُمكِن ضربه في 35 للحصولِ عَلى 70 وهو (2) ؛ فيُمكننا ضرب النسبة الأولى في (2) للحصول على النسبة الثالثة ؛ إذن: $100 \times 2 = 200$ 

ولمعرفة النسبة الثانية؛ نفكر في عملية تصلّح إذا نُفذت على النسبة الأولى دون التأثير على النسبة الثالثة. 

فمثلا نُبسط النسبة الأولى بالقسمة على (5) فيكون: $35 ÷ 5 = 7 , 100 ÷ 5 = 20$

وألاحظ أنّ إذا ضربت النسبة الثانية في (10) سنحصل على النسبة الثانية.

النسب المُتكافئة:   $100 : 35 , 20 : 7 , 200 : 70$

ويُمكن حل السؤال بالحصول على النسبة الثانية أولا وذلك بتبسيط النسبة ثم القيام بضرب النسبة الثانية في (10).

 

11) أَلْوانٌ: يُحَضِّرُ رَسّامٌ دَرَجَةً مِنْ دَرَجاتِ اللَّوْنِ الْبَنَفْسَجِيِّ بِإِضافَةِ قَطَراتٍ مِنَ اللَّوْنِ الأزْرَقِ إِلى قَطَراتٍ مِنَ اللَّوْنِ الأحْمَرِ بِنِسْبَةِ 5 : 3، كَمْ قَطْرَةً مِنَ اللَّوْنِ الَْزْرَقِ سَيَحْتاجُ إِلى إِضافَتِها إِلى 45 قَطْرَةً مِنَ اللَّوْنِ الأحْمَرِ؟ الجواب     27          3          اللون الأزرق     45 5 اللون الأحمر نقوم بإنشاء جدول النسب و بمقارنة أعمدة النسب نُلاحظ $5 \times 9 = 45$  ، إذن سيحتاج إلى 27 قطرة من اللون الأزرق. حيثُ أنّ: $3 \times 9 = 27$

 

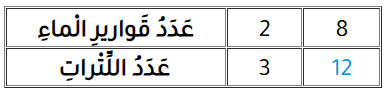
12) عَصائِرُ: يَضَعُ عامِلٌ في مَحَلٍّ لِلْعَصيرِ 12 مُكَعَّبَ سُكَّرٍ في $600 \mathrm{mL}$ مِنْ عَصيرِ الْكَرْكَديهْ. كَمْ مُكَعَّبَ سُكَّرٍ يَضَعُ في $250 \mathrm{mL}$ مِنْ عَصيرِ الْكَرْكَديهْ؟

الجواب

5	1	12	عدد مُكعبات السكر
250	50	600	كمية عصير الكركديه (mL)

نقوم بإنشاء جدول النسب؛ ونُلاحظ لا يوجد عدد صحيح يُمكن أن نقسمه العدد 600 عليه للحُصول على 250 ؛ لِذا نقلص العدد 600 بِاسْتِعمالِ الْقِسْمَةِ بدايةً؛ لأحصلَ على عددٍ يُمكن ضربهُ في عَدد صحيحٍ للحُصول على 250 ؛ وهنا نقْسِمُ طَرَفَيِ النِّسْبَةِ الأولى عَلى 12 

وبما أنّ $50 \times 5 = 250$ ، إذن؛ أَضْرِبُ 1 في 5؛ لأحْصُلَ عَلى عدد مُكعبات السكر في النِّسْبَةِ الثّالِثَةِ. 

إذن؛ عدد مُكعبات السكر اللازمة لعمل $250 \mathrm{mL}$ من عصير الكركديه يُساوي (5) مُكعبات.

---

13) بَسْتَنَةٌ: يَتَقاضى بُسْتانِيٌّ $20 \mathrm{JD}$ عَنْ كُلِّ 8 ساعاتِ عَمَلٍ، كَمْ يَتَقاضى عَنْ 10 ساعاتِ عَمَلٍ؟

الحل:

10	2	8	عدد ساعات العمل
25	5	20	المبلغ الذي يتقاضاه

نقوم بإنشاء جدول النسب؛ ونُلاحظ لا يوجد عدد صحيح يُمكن أن نضربه في 8 للحُصول على 10 ؛ لِذا نقلص العدد 8 بِاسْتِعمالِ الْقِسْمَةِ بدايةً؛ لأحصلَ على عددٍ يُمكن ضربهُ في عَدد صحيحٍ للحُصول على 10؛ وهنا نقْسِمُ طَرَفَيِ النِّسْبَةِ الأولى عَلى 4

وبما أنّ $2 \times 5 = 10$ إذن؛ أَضْرِبُ 5 في 5؛ لأحْصُلَ عَلى المبلغ الذي يتقاضاه البُستناني إذا عمل 10 ساعات.

إذن؛ المبلغ الذي سيتقاضاه البُستاني هو: 25 دينار.

---

أَكْتُبُ 3 نِسَبٍ تَصِفُ كُلَّ شَكْلٍ مِمّا يَأْتي:

14) نِسْبَةَ الأقْمارِ إِلى النُّجومِ. الجواب $6 : 12 , 2 : 4 , 1 : 2$

 

 

 

 

 

 

 

15) نِسْبَةَ الْوُجوهِ السَّعيدَةِ إِلى الْوُجوهِ الْحَزينَةِ. الجواب $15 : 4 , 30 : 8 , 45 : 12$

 

 

 

 

 

 

---

حلول أسئلة مهارات التفكير العُليا

أَكْتَشِفُ الْمُخْتَلِفَ: أَيُّ النِّسَبِ الآتِيَةِ مُخْتَلِفَةٌ عَنِ الْبَقِيَّةِ؟

 $\boxed{ 2 : 7 } \boxed{4 : 14} \boxed{6 : 20} \boxed{6 : 21}$

الجواب

النسبة المُختلفة هي: $6 : 20$  لأنها لا تُكافئ باقي النسب.  

---

17) أَكْتَشِفُ الْخَطَأَ: أُحَدِّدُ الْقيمَةَ الْخَطَأَ في جَدْوَلِ النِّسْبَةِ الْتي، وَأُصَحِّحُها:

64	16	4	عَدَدُ الْعُبُوّاتِ
36	12	3	السَّعَةُ بِاللِّتْرِ

الجواب

القيمة الخطأ هي: 36 ، والصواب أن تكون القيمة 48

حيثُ أن العدد 64 في النسبة الثالثة جاء من ضرب العدد 16 في 4.     $16 \times 4 = 64$

فإذن؛ $12 \times 4= 48$

---

18) تَبْريرٌ: قالَ رائِدٌ: النِّسْبَةُ 4 : 2 تُكافِئُ النِّسْبَةَ 18 : 9، هَلْ قَوْلُهُ صَحيحٌ؟ أُبَرِّرُ إِجابَتي.

الجواب

نعم؛ لأنّ     $9 : 18 \stackrel{÷9}{\to } 1 : 2$     والنسبة 2 : 1 تُكافئ النسبة 4 : 2

فإذن؛ $9 : 18 = 1 : 2 = 2 : 4$

---

19) تَحَدٍّ: لَدى هَناءَ مُكَعَّباتٌ حَمْراءُ وَزَرْقاءُ وَخَضْراءُ وَفْقَ النِّسَبِ الْمُبَيَّنَةِ أَدْناهُ، إِذا كانَ لَدَيْها 6 مُكَعَّباتٍ زَرْقَاءَ، فَكَمْ مُكَعَّبًا أَحْمَرَ لَدَيْها

أَحْمَرُ : أَخْضَرُ	أَخْضَرُ : أَزْرَقُ
2 : 5	1 : 3

الجواب

في العمود الأيسر لدينا (1) مُكعب أزرق ، و (3) مُكعبات خضراء. وفي العمود الأيمين لدينا (2) مُكعب أخضر، و (5) مُكعبات حمراء.

ولتسهيل الحل وتفادي الوقوع في الخطأ ، قم بإنشاء جدولا نسب، كما يلي:

6	1	عدد المكعبات الزرقاء
?	3	عدد المكعبات الخضراء

هنا بما أن $1 \times 6 = 6$  إذن؛ أَضْرِبُ 3 في 6؛ لأحْصُلَ عَلى عدد المُكعبات الخضراء في النسبة الثانية . $3 \times 6 = 18$

إذن؛ إذا كان لدى هناء 6 مُكعبات زرقاء فيكون لديها 18 مُكعب أخضر. ولكن المطلوب هو عدد المُكعبات الحمراء.

فنستعين بجدول النسب التالي:

18	2	عدد المكعبات الخضراء
?	5	عدد المكعبات الحمراء

هنا بما أن $2 \times 9 = 18$ إذن؛ أَضْرِبُ 5 في 9؛ لأحْصُلَ عَلى عدد المُكعبات الحمراء في النسبة الثانية.  $5 \times 9 = 45$

إذن؛ إذا كان لدى هناء 6 مُكعبات زرقاء فسيكون لديها (45) مُكعب أحمرء.

---

20) أََكْْتب أَصِفُ طَريقَةَ إيجادِ نِسْبَةٍ مُكافِئَةٍ لِنِسْبَةٍ مُعْطاةٍ؟

الجواب

أضربُ طرفي النسبة في نفس العدد، أو أقسم طرفيها على نفس العدد.

---

حلول أسئلة كتاب التمارين

أَجِدُ لِكُلِّ نِسْبَةٍ مِمّا يَأْتي نِسْبَةً تُكافِئُها:

$\mathbf{2}\mathbf{)} 63 : 72 \stackrel{÷9}{\to } 7 : 8$	$\mathbf{1}\mathbf{)}\mathbf{ } 7 : 11 \stackrel{\times 2}{\to } 14 : 22$
$\mathbf{4}\mathbf{)} 32 : 16 \stackrel{÷4}{\to } 8 : 4$	$\mathbf{3}\mathbf{)} 9 : 3 \stackrel{÷3}{\to } 3 : 1$

 

 

 

أُكْمِلُ جَدْوَلَ النِّسْبَةِ في كُلٍّ مِمّا يَأْتي، ثُمَّ أَكْتُبُ النِّسَبَ الْمُتَكافِئَةَ:

5)

35	10	5	عَدَدُ الْحافِلاتِ
700	200	100	عَدَدُ الْمَقاعِدِ

 

 

النِّسَبَ الْمُتَكافِئَةَ: $5 : 100 , 10 : 200 , 35 : 700$

6)

8	2	عَدَدُ أَكْياسِ الاسْمَنْتِ
560	140	عَدَدُ لِتْراتِ الْماءِ

 

 

النِّسَبَ الْمُتَكافِئَةَ: $2 : 140 , 8 : 560$

---

أُكْمِلُ الْفَراغَ بِكِتابَةِ الْعَدَدِ الْمَفْقودِ لِتَكْوينِ نِسَبٍ مُتَكافِئَةٍ:

$\mathbf{8}\mathbf{)}\mathbf{ }21 : 56 = 3 : 8$	$\mathbf{7}\mathbf{)} 16 : 8 = 2 : 1$
$\mathbf{10}\mathbf{)} 42 : 35 = 6 : 5$	$\mathbf{9}\mathbf{)}\mathbf{ }12 : 30 = 2 : 5$

 

 

 

11) أَلْوانٌ: يُكَوِّنُ عِصامٌ دَرَجَةً مِنْ دَرَجاتِ اللَّوْنِ الزَّهْرِيِّ بدَِمْجِ  $15 \mathrm{mL}$ مِنَ اللَّوْنِ الأحَْمَرِ مَعَ $6 \mathrm{mL}$ مِنَ اللَّوْنِ الأبَْيضَِ. كَمْ لِتْرًا مِنَ اللَّوْنِ الأبْيَضِ يَدْمِجُ مَعَ $5 \mathrm{L}$ مِنَ اللَّوْنِ الأحْمَرِ؟

الجواب

يحتاج عصام إلى $\text{ 2 L}$ من اللون الأبيض ليدمجها مع $5 \mathrm{L}$ من اللون الأحمر.

 

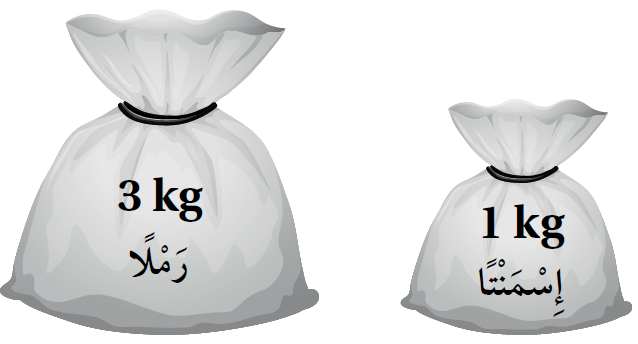12) إِسْمَنْتٌ: يَخْلِطُ عامِلُ بِناءٍ الْكَمِّيَّتَيْنِ الْمُوَضَّحَتَيْنِ في الشَّكْلِ الْمُجاوِرِ مِنَ الاسْمَنْتِ وَالرَّمْلِ لِعَمَلِ خَلْطَةِ الاسْمَنْتِ اللّازِمَةِ لِلْبِناءِ، ما كُتْلَةُ الاسْمَنْتِ وَالرَّمْلِ الَّتي يَحْتاجُ إِلَيْها لِعَمَلِ خَلْطَةٍ كُتْلَتُها $20 \mathrm{kg}$ ؟ الجواب يحتاج العامل إلى $5 \mathrm{Kg}$ من الاسمنت ، و $15 \mathrm{Kg}$ من الرمل لعمل خلطة كُتلتها $20 \mathrm{Kg}$.