رياضيات فصل ثاني

حلول أسئلة أتحقق من فهمي 

تمثّلُ البياناتُ الآتيةُ عددَ السُّعراتِ الحراريةِ في عددٍ مِنْ حبّاتِ الفاكهةِ. أَجِدُ الوسيطَ وَالمِنوالَ لهذهِ البياناتِ. 

38, 50, 44, 29, 94, 56, 38, 47

الوسيط : نعيد ترتيب البيانات تصاعدياً 29,38,38,44,47,50,56,94

البيانات زوجية ، نأخذ الوسط الحسابي للعددين الأوسطين 

$\overline{\mathrm{x}}=\frac{44+47}{2}=45.5$

المنوال : العدد الأكثر تكراراً هو 38

 

يبيّنُ الجدولُ المجاورُ أسعارَ عُبوّاتِ عطورٍ بِالدينارِ في محلَّينِ مختلفَينِ. أَجِدُ مدى أسعارِ عُبوّاتِ العطورِ في كلِّ محلٍّ ، ثمَّ أحددُ المحلَّ الّذي فيهِ أسعارُ عبوّاتِ العطورِ أكثرُ تجانسًا.

المحل الأول	المحل الثاني
88       44        55    23       40       140    50      35	78       45         50     95       65         61     40       75

140-23 = المحل الأول : أكبرُ قِيَمِ البياناتِ هِيَ 140 ، وَأصغرُ القِيَمِ هِيَ 23، إذنْ، المدى هُوَ: 117

95-40 = المحل الثاني : أكبرُ قِيَمِ البياناتِ هِيَ 95 ، وَأصغرُ القِيَمِ هِيَ 40 ، إذنْ، المدى هُوَ: 55

إذنْ، اسعار العبوات في المحل أكثرُ تجانسًا؛ لأنَّ قيمةَ المدى لِكُتلِهِمْ أقلُّ.

 

4) تريدُ مريمُ أنْ تعرفَ متوسطَ لونِ العيونِ في صفِّها.

ألوانُ العيون في صفها بياناتٌ غيرُ عدديةٍ، لِذلكَ لا يمكنُ وصفُها بِاستعمالِ الوسطِ الحسابيِّ أَوِ الوسيطِ أَوِ المَدى. إذنْ، المقياسُ الوحيدُ الّذي يمكنُ استعمالُهُ لِوصفِ هذِهِ البياناتِ هُوَ المِنوالُ 

5) يريدُ ريّانُ إيجادَ مركزِ القيمِ الآتيةِ الّتي تمثلُ درجاتِ زُملائِهِ في امتحانِ مادّةِ العلومِ: 

15    18   15   12   15   17   14   15   15 

البيانات متقاربة ولا يوجد فيها قيم متطرفة ، نستخدم الوسط الحسابي 

---

حلول أسئلة أتدرب وأحل المسائل 

 طقسٌ: قاسَتْ شروقُ كمّيةَ هَطلِ الأمطارِ في حديقةِ منزلِها خلالَ 14 يومًا مِنْ شهرِ كانونِ الأولِ، وَسجّلَتِ القِيَمَ كما يأتي:

1.5 cm           3.9 cm            0.0 cm            0.7 cm            0.0 cm      5.9 cm           2.4 cm            3.4 cm            4.7 cm            0.0 cm      2.1 cm           4.5 cm            1.7 mm           3.1 cm

أَجِدُ:

1) الوسيطَ: نرتب البيانات تصاعدياً (انتبه لوجود قيمة 1.7mm=0.17cm)

أعد ترتيب البيانات $0.0, 0.0, 0.0,\mathbf{0}\mathbf{.}\mathbf{17}, 0.7, 1.5 , 2.1, 2.4, 3.1, 3.4 , 3.9 , 4.5 , 4.7 , 5.9$

$\frac{2.1+2.4}{2}=\frac{4.5}{2}=2.25$

2) الوسطَ الحسابيَّ:

$$\begin{gathered} \overline{\mathrm{x}}=\frac{\left(3\times 0\right)+0.17+0.7+1.5+2.1+2.4+3.1+3.4+3.9+4.5+4.7+5.9 }{14} \\ =\frac{32.37}{14}=2.31 \end{gathered}$$

3) المِنوالَ: العدد الأكثر تكراراً هو 0

4) المَدى: الفرقَ بينَ أكبرِ قِيَمِ البياناتِ وَأصغرِها

$5.9-0=5.9$

 

5) أسرةٌ: سألَتْ أسماءُ بعضَ طالباتِ صفِّها عَنْ عددِ إخوانِهِنَّ، ثمَّ مثّلَتِ الإجاباتِ كَما في الشكلِ أدناهُ. أَجِدُ الوسيطَ وَالوسطَ الحسابيَّ، ثمَّ أحدّدُ أيُّهما أفضلُ لِوصفِ مركزِ هذِهِ البياناتِ.

البيانات : $0,1,1,1,2,2,2,2,3,7$

الوسيط : البيانات زوجية ، ناخذ متوسط العددين الأوسطين 

$\frac{2+2}{2}=2$

الوسط الحسابي : 

$\mathrm{x}=\frac{0+1+1+1+2+2+2+2+3+7}{10}=2.1$

الوسيط أفضل لأن البيانات تحتوي على قيمة متطرفة تأثر على ايجاد الوسط الحسابي 

 

عبدُاللهِ وَكِنانُ سبّاحانِ يتنافسانِ دائمًا في البطولاتِ، وَيبيّنُ الجدولُ الآتي ملخَّصًا لِلنتائجِ الّتي أحرزاها في آخِرِ 10 بطولاتٍ. بناءً عَلَيْهِ، أكملُ الجملَ الآتيةَ:

المَدى (بِالثواني)	الوسيطُ (بِالثواني)
3.9	72.3	عبدالله
7.2	71.6	كنان

6) كنان أسرعُ بِالمتوسطِ مِنْ عبد الله  . لان وسيط كنان أقل زمناً من عبد الله 

7) النتائجُ الّتي يحرزُها عبد الله منسجمةٌ أكثرَ مِنَ النتائجِ الّتي يحرزُها كنان . لان المدى أقل عند  عبد الله 

 

أحدّدُ ما إذا كانَ يجبُ استعمالُ الوسطِ الحسابيِّ أمِ الوسيطِ أمِ المِنوالِ أمِ المدى في كلٍّ مِنَ المواقفِ الآتيةِ:

8) تريدُ منارُ أنْ تجدَ مركزَ القِيَمِ الآتيةِ وَالّتي تمثّلُ أعمارَ 7 مِنْ أفرادِ عائلتِها:

12       34        25        18       32       88     5

يوجد قيم متطرفة في البيانات ، الوسيط هو الأفضل = 25

9) يريدُ معلمُ الرياضياتِ تحديدَ الدرجةِ الّتي نصفُ درجاتِ الطلبةِ أقلُّ مِنْها.

نستخدم الوسيط وذلك عبر ترتيب العلامات تصاعدياً ويكون نصف درجات الطلبة أقل منها 

 

 أَجِدُ القِيَمَ الممكنةَ جَميعَها لِلعددِ المجهولِ على البطاقةِ السابعةِ في كلٍّ مِنَ الحالاتِ الآتيةِ:

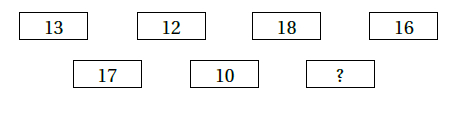
نعيد ترتيب البيانات : 10,12,13,16,17,18

10) إذا كانَ وسيطُ الأعدادِ السبعةِ يساوي 14

10,12,13,14,16,17,18

العدد المجهول هو 14 

11) إذا كانَ وسيطُ الأعدادِ السبعةِ يساوي 16

$10,12,13,\mathbf{16},17,18,\mathbf{X}$

العدد المجهول هو أي عدد أكبر من 18 

12) إذا كانَ وسيطُ الأعدادِ السبعةِ يساوي 13 وَالمَدى يساوي 9

x,10,12,13,16,17,18

الوسيط = 13 ، يعني أن العدد أقل من 10  

المدى = أكبر قيمة - أقل قيمة 

$$\begin{gathered} 18-\mathrm{x}=9 \\ \mathrm{x}=9 \end{gathered}$$

العدد المجهول هو 9 

 

13) تبريرٌ: إذا كانَ الوسيطُ لِلقيمِ المرتَّبةِ تصاعديًّا $\mathbf{2}\mathbf{,}\mathbf{3}\mathbf{,}\mathbf{ }\mathbf{\Delta }\mathbf{,}\mathbf{ }\mathbf{\square }\mathbf{,}\mathbf{8}\mathbf{,}\mathbf{12}$ يساوي 6، فَأَجِدُ . القِيَمَ الممكنةَ جميعَها لِكلٍّ مِنْ $\mathbf{∆}\mathbf{,}\mathbf{\square }$

البيانات زوجية : الوسيط = متوسط القيمتين في اللتان يتوسطان البيانات 

$$\begin{gathered} \frac{△+\square }{2}=6 \\ △+\square =12 \end{gathered}$$       البيانات الممكن هي الأعداد التي تقع بين 3 و 8 ومجموعهما يساوي 12  $$\begin{gathered} \square =6,△=6 \\ \square =7,△=5 \end{gathered}$$

14) مسألةٌ مفتوحةٌ: أكتبُ مجموعةَ أعدادٍ وسطُها الحسابيُّ 28 ، وَوسيطُها 29 . وَمَداها 18

$19,22,24,29,31,34,37$

 

15) مسألةٌ مفتوحةٌ: أصفُ موقفًا حياتيًّا لا يكونُ فيهِ استعمالُ الوسطِ الحسابيِّ مناسبًا لِوصفِ مركزِ البياناتِ، ثمَّ أحدّدُ المقياسَ الأنسبَ لِوصفِ هذِهِ البياناتِ. 

البيانات المتعلقة بالوان أقمشة في محل ملابس ، بيانات غير عددية لا يكون الوسط الحسابي مناسباً لوصف مركزها ، ويستخدم المنوال 

 

16) مسألةٌ مفتوحةٌ : أكتبُ مثالً لبياناتٍ يكونُ فيها الوسطُ الحسابيُّ يساوي الوسيطَ وَيساوي قيمةَ المنوالِ.

$10,20,20,20,30$

 

17) أكتبُُ كيفَ أحددُ المقياسَ الأنسبَ لوصفِ البياناتِ؟

الوسط الحسابي : بيانات عددية وغير متباعدة (لا يوجد من ضمنها قيم متطرفة)

الوسيط : بيانات عددية و البيانات المتباعدة التي من ضمنها قيم متطرفة

المنوال : البيانات الغير عددية 

المدى : تحديد البيانات الأكثر تجانساً 

---

---

حلول أسئلة كتاب التمارين 

 تمثّلُ البياناتُ المجاورةُ أطوالَ 15 نبتةً لِقربِ جزءٍ مِنْ عشرةٍ مِنَ السنتيمترِ. أَجِدُ:

14.6	13.2	12.8	15.3	19.1
17.5	13.5	14.8	18.4	20.0
17.3	17.6	18.1	16.7	14.4

1) الوسطَ الحسابيَّ

$$\begin{gathered} \overline{x}=\frac{14.6+13.2+12.8+15.3+19.1+17.5+13.5+14.8+18.4+20.0+17.3+17.6+18.1+16.7+14.4}{15} \\ =\frac{243.3}{15} = 16.22 \end{gathered}$$

2 ) الوسيطَ 

نعيد ترتيب البيانات 

$12.8,13.2,13.5,14.4,14.6,14.8,15.3,16.7,17.3,17.5,17.6,18.1,18.4,19.1,20$

الوسيطَ=16.7

3) هلْ يمكنُ إيجادُ المِنوالِ لِأطوالِ النباتاتِ؟ أبرّرُ إجابتي.

لا، لان البيانات لا يوجد فيها تكرار 

 

يبيّنُ الجدولُ المجاورُ عددَ العاملينَ في أحدِ المكاتبِ في 40 يومًا مختلفًا: 

عدد العاملين	11	12	13	14	15	16
التكرار	3	7	11	9	8	2

4) يقولُ سائدٌ : "إِنَّ الوسطَ الحسابيَّ لِعددِ العاملينَ في  اليومِ الواحدِ أكبرُ مِنَ المِنْوالِ" هلْ قولُهُ صحيحٌ؟ أبيّنُ ذلكَ بِالحلِّ.

الوسط : $$\begin{gathered} x=\frac{\left(3\times 11\right)+\left(7\times 12\right)+\left(13\times 11\right)+\left(9\times 14\right)+\left(8\times 15\right)+\left(2\times 16\right)}{40} \\ =\frac{538}{40}=13.45 \end{gathered}$$

المنوال : الأكثر تكرارأً = 13 

مقولة سائد صحيحة 

 

أحدّدُ ما إذا كانَ يجبُ استعمالُ الوسطِ الحسابيِّ أمِ الوسيطِ أمِ المِنوالِ أمِ المدى في كلٍّ مِنَ المواقفِ الآتيةِ: 

5) تصنعُ رزانُ ملابسَ بِثلاثةِ مقاساتٍ: صغيرٍ، وَوسطٍ، وَكبيرٍ، وَتريدُ معرفةَ متوسطِ المقاساتِ.

الوسط الحسابي 

6) يتقاضى 30 موظَّفًا رواتبَ مِنَ الشركةِ الّتي يعملونَ بِها. يُريد صاحبُ العملِ معرفةَ الراتبِ الّذي يتقاضى نصفُ الموظَّفينَ أقلَّ مِنْهُ.

الوسيط 

7) تراقبُ إدارةُ المرورِ سرعةَ السيّاراتِ على طريقٍ سريعٍ، وَتريدُ الإدارةُ معرفةَ تقارُبِ سُرُعاتِ السيّاراتِ أَوْ تباعدِها.

المدى 

 

8 )فكّرَ كلٌّ مِنْ قاسمٍ وَماجدةَ بِمجموعةٍ مِنَ الأعدادِ فَكانَتْ كَما يأتي:

10        12            ?         ? أعدادُ قاسمٍ

3        6         7       12 أعدادُ ماجدةَ

 إذا كانَ عددانِ مِنْ أعدادِ قاسمٍ مفقودَينِ، وَكانَ الوسطُ الحسابيُّ لِأعدادِهِ يزيدُ عَنِ الوسطِ الحسابيِّ لِأعدادِ ماجدةَ بِمقدارِ 2، وَكانَ مَدى أعدادِ قاسمٍ وَمَدى أعدادِ ماجدةَ متساويَينِ، أَجِدُ العددَينِ المفقودَينِ.

الوسط الحسابي لأعداد ماجدة $\frac{28}{4}=7$ والمدى 9 = 3-12

الوسط الحسابي لقاسم = 9 

مجموع الأعداد لدى قاسم = الوسط × عددهم = 36

نجد مجموع الرقمين الفقودين = $$\begin{gathered} 36-\left(10+12+\right)+\mathbf{(}\mathbf{x}\mathbf{+}\mathbf{y}\mathbf{)} \\ \mathrm{x}+\mathrm{y}=14 \end{gathered}$$

نستخدم المدى $$\begin{gathered} 12-\mathrm{y}=9 \\ \mathrm{y}=3 \end{gathered}$$

العدد الثاني $$\begin{gathered} \mathrm{y}+\mathrm{x}=14>>>\mathrm{y}=3 \\ \mathrm{x}=11 \end{gathered}$$