رياضيات فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين

حلول أسئلة أتحقق من فهمي

أتحقق من فهمي صفحة 109

$ABCD$ مستطيل إِحداثيات رؤوسه هي: $A (-4, -3), B (-4, -1), C (-1, -1), D (-1, -3)$

3) أرسم المستطيل $A\text{'}B\text{'}C\text{'}D\text{'}$ الذي هو انعكاس للمستطيل $ABCD$ حول المحور $x$ ، ثم أحدد إحداثيات رؤوسه.

الحل :  

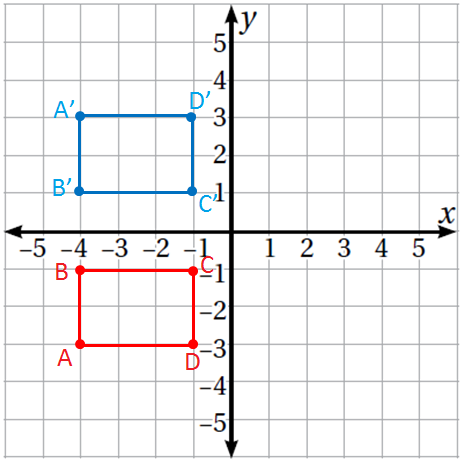
إحداثيات رؤوس المستطيل $A\text{'}B\text{'}C\text{'}D\text{'}$ هي : $A\text{'}(-4 , 3) , B\text{'}(-4 , 1) , C\text{'}(-1 , 1) , D\text{'}(-1 , 3)$

---

 

4) أرسم المستطيل $A"B"C"D"$ الذي هو انعكاس للمستطيل $ABCD$ حول المحور $y$ ، ثم أحدد إحداثيات رؤوسه.

الحل :  

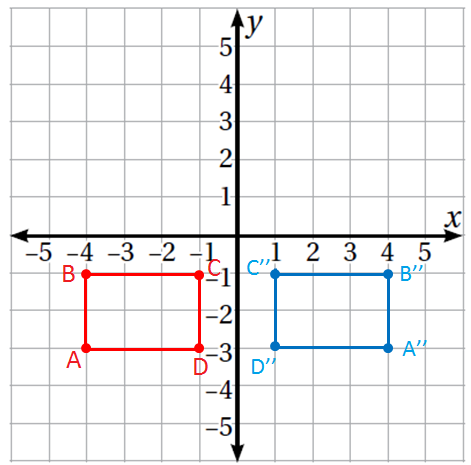
إحداثيات رؤوس المستطيل $A"B"C"D"$ هي : $A\text{'}\text{'}(4 , -3) , B\text{'}\text{'}(4 ,-1) , C\text{'}\text{'}(1 ,-1) , D\text{'}\text{'}(1 , -3)$

---

أتحقق من فهمي صفحة 110

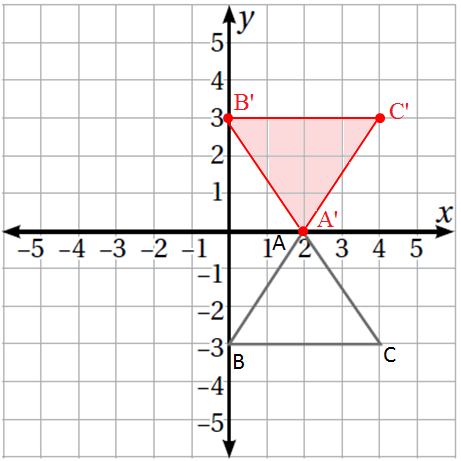
$ABC$ مثلث إِحداثيات رؤوسه: $A (-4, -3), B (-4, -1), C (-1,-1)$ أكتب إحداثيات صور رؤوسه بالانعكاسِ حول المحور $y$ ، ثم أرسم المثلث وصورته.

الحل :   

الخطوة 1 : أكتب إحداثيات الرؤوس

$A(x , y) \to A\text{'}(-x , y)$

$A(-4 , -3) \to A\text{'}(4 , -3)$

$B(-4 , -1) \to B\text{'}(4 , -1)$

$C(-1 , -1) \to C\text{'}(1 , -1)$

الخطوة 2 : أرسم الشكل وصورته 

---

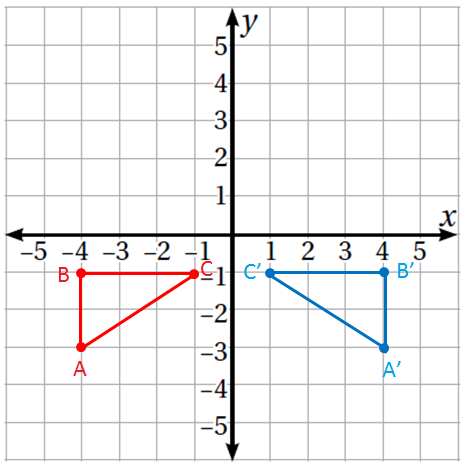
أتحقق من فهمي صفحة 111 هندسة: رسم مهند شكل سمكة في المستوى الإحداثي المجاور، رؤوسه:  $.A, B, C, D, E, F$  أجد إحداثيات صورة رؤوس شكل السمكة بالانعكاس حول المحور $x\hspace{0.17em}$  ، ثمّ أمثّلُها في المُستوى الإحداثي.

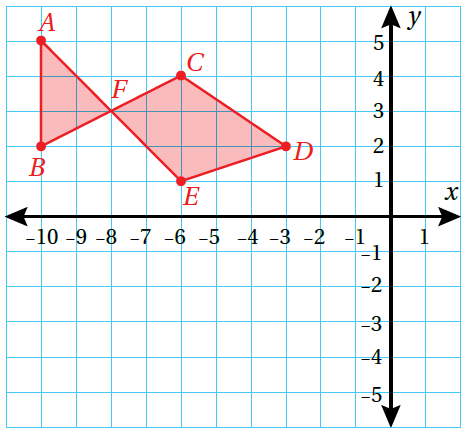الحل :   

الخطوة 1 : أكتب إحداثيات الرؤوس

$A(x , y) \to A\text{'}(x , - y)$

$A(-10 , 5) \to A\text{'}(-10 ,-5)$

$B(-10 , 2) \to B\text{'}(-10 ,-2)$

$C(-6 , 4) \to C\text{'}(-6 ,-4)$

$D(-3 , 2) \to D\text{'}(-3 ,-2)$

$E(-6 , 1) \to E\text{'}(-6 ,-1)$

$F(-8 , 3) \to F\text{'}(-8 , -3)$

الخطوة 2 : أرسم الشكل وصورته 

---

أسئلة أتدرب وأحل المسائل

أرسم صورة الشكل بالانعكاس حول المحور المعطى، ثم أحدد إحداثيات رؤوسها في كل مما يأتي:

الحل : 

1) الانعكاس حول المحور y

إحداثيات رؤوس المثلث $A\text{'}B\text{'}C\text{'}$ هي : $A\text{'}(-1 , 3) , B\text{'}(-5 , 2) , C\text{'}(-4 , -2)$

---

 2) الانعكاس حول المحور x

إحداثيات رؤوس المثلث $L\text{'}M\text{'}N\text{'}$ هي : $L\text{'}(2 , -4) , M\text{'}(4 , -2) , N\text{'}(-2 , -1)$

 

---

 

أكتب إحداثيات صور رؤوس كل شكلٍ مما يأتي بالانعكاس حول المحور y ، ثم أمثل الشكل وصورته:

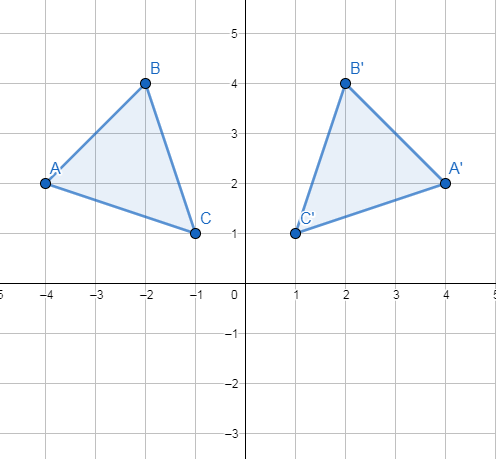
3) Q (-4, 2) , R (-2, 4) , S (-1, 1)

الحل :

أجد إحداثيات صور رؤوس المثلث $Q\text{'} R\text{'}S\text{'}$

قاعدة الانعكاس حول المحور y  $A(x , y) \to A\text{'}(-x , y)$

         $$\begin{gathered} Q(-4 , 2) \to Q\text{'} (4 , 2) \\ R(-2 , 4) \to Q\text{'} (2 , 4) \\ S(-1 , 1) \to Q\text{'} (1 , 1) \end{gathered}$$

أرسم الشكل وصورته  

 

---

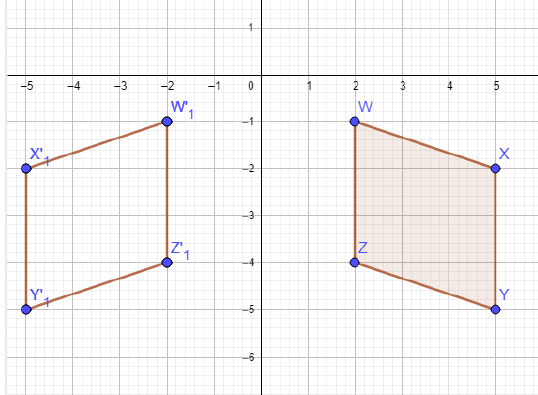
4) W (2, -1) , X (5, -2) , Y (5, -5) , Z (2, -4) 

الحل :

أجد إحداثيات صور رؤوس الشكل الرباعي $W\text{'} X\text{'} Y\text{'} Z\text{'}$

قاعدة الانعكاس حول المحور y  $A(x , y) \to A\text{'}(-x , y)$

$$\begin{gathered} W(2 , -1) \to W\text{'} (-2 , -1) \\ X(5 , -2) \to X\text{'} (-5 , -2) \\ Y(5 , -5) \to Q\text{'} (-5 , -5) \\ Z(2 , -4) \to Z\text{'} (-2 , -4) \end{gathered}$$

أرسم الشكل وصورته  

---

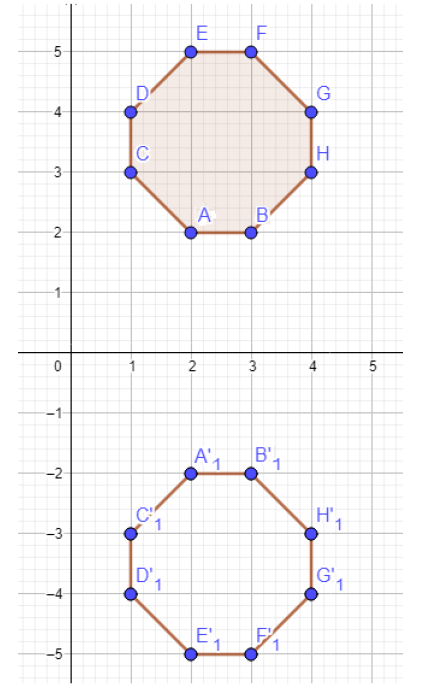
5) أرسم في المستوى الإحداثي شكلًا ثمانيًا، إحداثيات رؤوسه: 

$.A (2, 2), B (3, 2), C (1, 3), D (1, 4), E (2, 5), F (3, 5), G (4, 4), H (4, 3)$

بعد ذلك أرسم صورة الانعكاس له حول المحور x ، ثم أكتب إحداثيات رؤوسه بعد عملية الانعكاس. 

الحل :

إحداثيات رؤوس الشكل بعد عملية الانعكاس حول المحور y هي : 

$A (2 , 2) \to A\text{'} (2 , -2)$

$B (3 , 2) \to B\text{'} (3 , -2)$

$C (1 , 3) \to C\text{'} (1 , -3)$

$D (1 , 4) \to D\text{'} (1 , -4)$

$E (2 , 5) \to E\text{'} (2 , -5)$

$F (3 , 5) \to F\text{'} (3 , -5)$

$G (4 , 4) \to G\text{'} (4 , -4)$

$H (4 , 3) \to H\text{'} (4 , -3)$

 

---

أحدد محور الانعكاس إذا علمت نقطة وصورتها في كل مما يأتي : 

6)  A (-3, 5)  $\to$  A' (3, 5)

7) B (2, -2) $\to$ B' (2, 2)

الحل :

6) المحور y : قاعدة الانعكاس حول المحور y  $A(x , y) \to A\text{'}(-x , y)$

7) المحور x : قاعدة الانعكاس حول المحور x  $A(x , y) \to A\text{'}(x , - y)$

---

 

حلول أسئلة مهارات التفكير العُليا

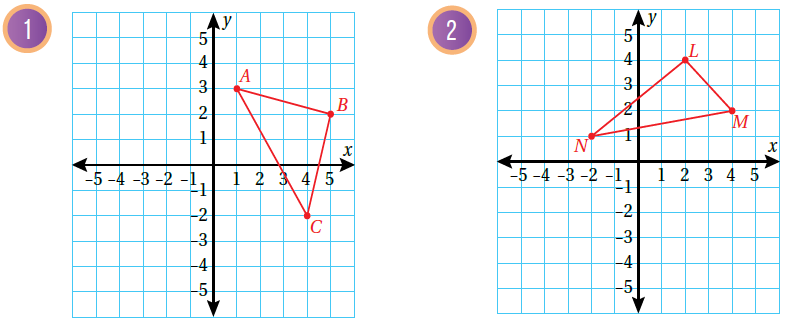
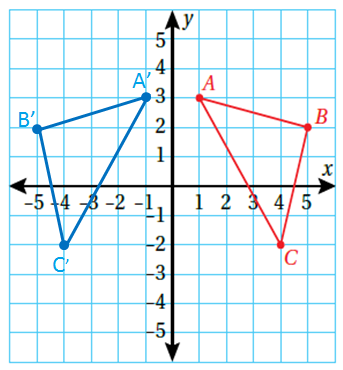
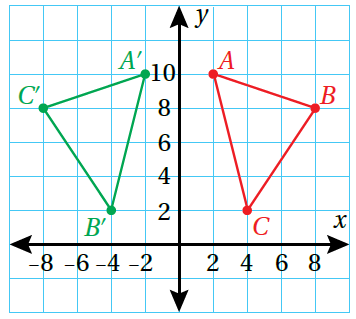
8) أكتشف الخطأ : رسم أحمد المثلث$ABC$ في المستوى الاحداثي المجاور، ثم عمل انعكاسًا له حول المحور $y$  أكتشف الخطأ في حل أحمد، ثم أصححه.

 

 

  

 

 

 

 

 

 

الحل :

أخطأ أحمد في التسمية إذ يجب تبديل $B\text{'}$ مع $C\text{'}$

التصحيح : 

---

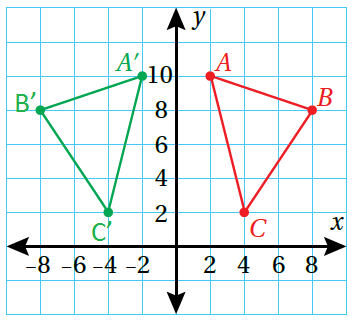
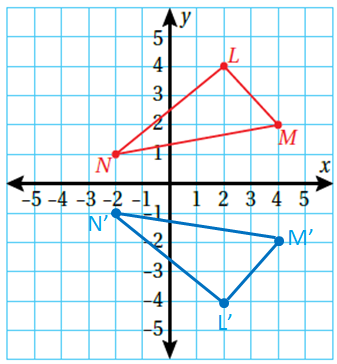
تحدّ : رسمت آمنة في المستوى الإحداثي مثلثًا إحداثيات رؤوسه $A(1 , 1) , B(2 , 3) , C(4 , 2)$ ثمّ عملت انعكاسًا للمثلث حول المحور y

لينتج المثلث $A\text{'}B\text{'}C\text{'}$ ، ثمّ عملت انعكاسًا للمثلث $A\text{'}B\text{'}C\text{'}$ حول المحور x لينتج المثلث  $A\text{'}\text{'}B\text{'}\text{'}C\text{'}\text{'}$ :   

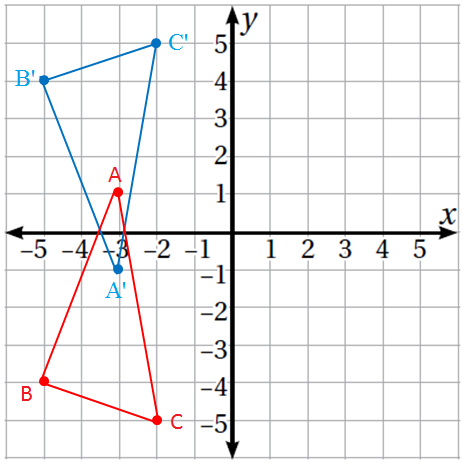
9) أجد إحداثيات كل من النقاط : $A\text{'} , B\text{'} , C\text{'}$  ، والنقاط : $A\text{'}\text{'} , B\text{'}\text{'} , C\text{'}\text{'}$

الحل :

الإحداثيات  : $A\text{'}(-1 , 1) , B\text{'}(-2 , 3) , C\text{'}(-4, 2)$  ،  $A\text{'}\text{'}(-1 ,-1) , B\text{'}\text{'}(-2 ,-3) , C\text{'}\text{'}(-4 , -2)$

 

---

10) أقارن الإحداثيات، ثم أبين كيف يمكن إيجاد إحداثيات النقاط $A\text{'}\text{'}B\text{'}\text{'}C\text{'}\text{'}$ مباشرة من إحداثيات النقاط $A\text{'}B\text{'}C\text{'}$

الإجابة :

أبدل اشارات كل من الاحداثيين x و y .

 

---

أسئلة كتاب التمارين

أكتب إحداثيات صور رؤوس كل شكلٍ مما يأتي بالانعكاس حول المحور x، ثم أمثل الشكل وصورته على المستوى الإحداثي نفسه :

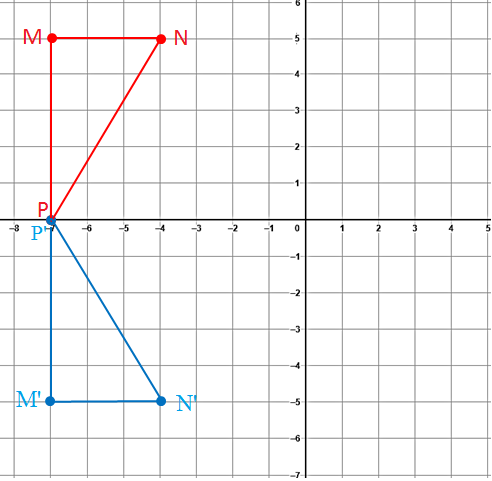
1) A (-3, 1) , B (-5, -4) , C (-2 , -5)                               2) M (-7 , 5) , N (-4 , 5) , P (-7 , 0)

الحل :

1) A (-3, 1) , B (-5, -4) , C (-2 , -5)

 إحداثيات رؤوس الشكل بعد عملية الانعكاس حول المحور x هي : $A\text{'}(-1 , 3) , B\text{'}(-5 , 2) , C\text{'}(-4 , -2)$

---

 2) M (-7 , 5) , N (-4 , 5) , P (-7 , 0)

 إحداثيات رؤوس الشكل بعد عملية الانعكاس حول المحور x هي : $M\text{'}(-7 , -5) , N\text{'}(-4 , -5) , P\text{'}(-7 , 0)$

 

---

أكتب إحداثيات صور رؤوس كل شكلٍ مما يأتي بالانعكاس حول المحور y، ثم أمثل الشكل وصورته على المستوى الإحداثي نفسه:

3) Q (3 , 9) , R (10 , 7) , S (6 , 4)

4) W (-6 , 5) , X (-6 , 2) , Y (-2 , 2) , Z (-2 , 6)    

 الحل :

3) Q (3 , 9) , R (10 , 7) , S (6 , 4)

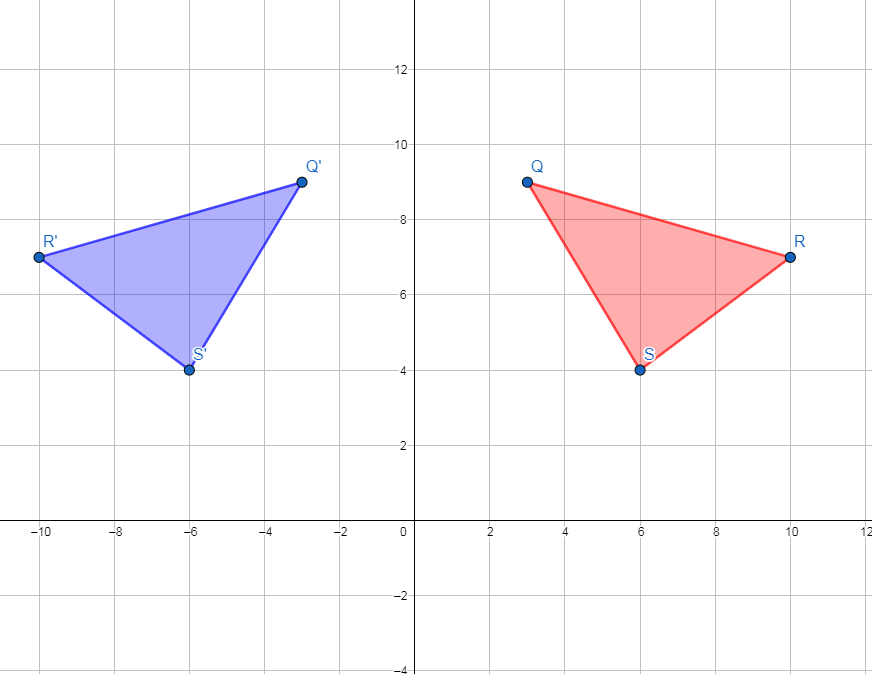
إحداثيات صور الرؤوس :  $Q\text{'} (-3 , 9) , R\text{'} (-10 , 7) , S\text{'} (-6 , 4)$
 

---

 4) W (-6 , 5) , X (-6 , 2) , Y (-2 , 2) , Z (-2 , 6) 

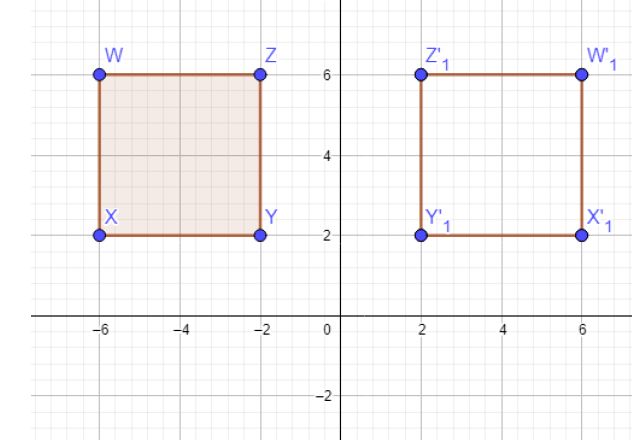
إحداثيات صور الرؤوس : $W \text{'} (6 , 5) , X \text{'}(6 , 2) , Y \text{'}(2 , 2) , Z \text{'} (2 , 6)$

---

 

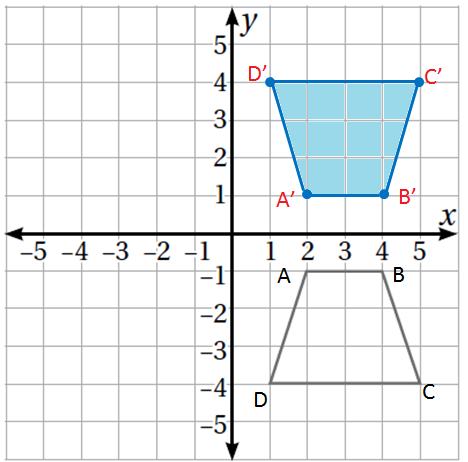
5) أجد في ما يأتي إحداثيات صورة شبه المنحرف بالانعكاس حول المحور x، ثم أرسُمُها:

 

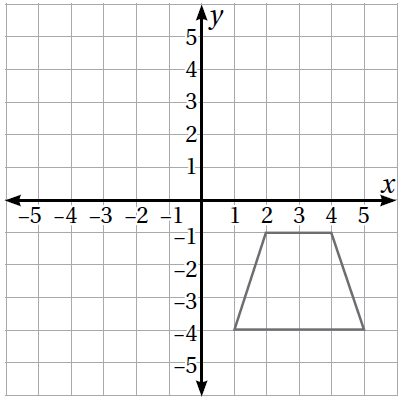
 الحل :

إحداثيات صور رؤوس شبه المنحرف : $A\text{'}(2 , 1) , B\text{'}(4 , 1) , C\text{'} (5 , 4) , D\text{'}(1 , 4)$   

 

---

 

6) أجد في ما يأتي إحداثيات صورة المثلث بالانعكاس حول المحور x، ثم أرسُمُها:

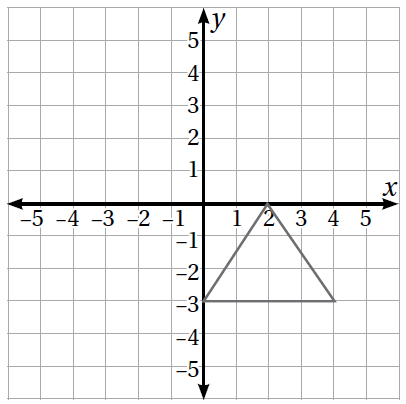
 الحل :

إحداثيات صور رؤوس المثلث : $A\text{'}(2 , 0) , B\text{'}(0 , 3) , C\text{'} (4 , 3)$

---

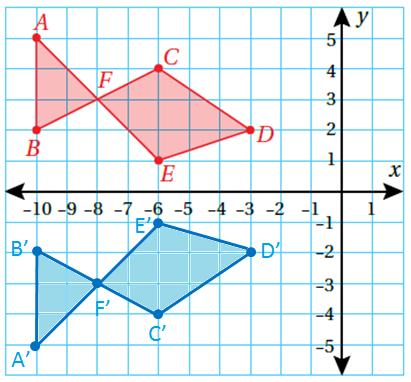
7) أصف الانعكاسات التي أجريت للشكل ABCD بهدف الانتقال إلى الشكل $A\text{'}\text{'}B\text{'}\text{'}C\text{'}\text{'}D\text{'}\text{'}$ 

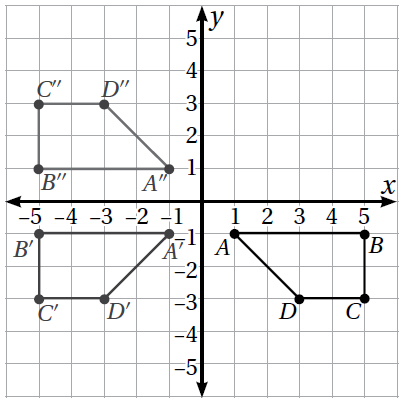
الإجابة : 

أُجري للشكل ABCD إنعكاسًا حول المحور y ، فنتج الشكل $A\text{'}B\text{'}C\text{'}D\text{'}$ ، ثمّ أجري إنعكاسًا للشكل $A\text{'}B\text{'}C\text{'}D\text{'}$ حول المحور x فنتج

الشكل $A\text{'}\text{'}B\text{'}\text{'}C\text{'}\text{'}D\text{'}\text{'}$.

---