رياضيات10 فصل أول

أتحقق من فهمي صفحة 39

يبين الشكل المجاور دائرة مركزها O. اسمي:

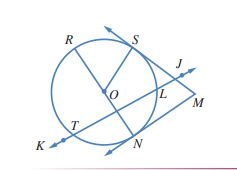
a) قاطعا للدائرة      $\overleftrightarrow{KJ}$

b) وترا للدائرة      $\overline{TL} or \overline{RN}$

c) مماسا للدائرة         $\overrightarrow{MN} or \overrightarrow{MS}$

---

أتحقق من فهمي صفحة 40

في الشكل المجاور، $\overline{CD} و \overline{AB}$  وتران في دائرة مركزها O. إذا كان $OM=ON$، و $CN=12cm$، فما طول $\overline{AB}$؟ 

$CN=12 cm$

$$$\overline{CD} =24 cm \left(\overline{CD} \mathrm{نصف} \mathrm{هو} CN \mathrm{لان}\right)$

$\overline{AB }=24cm \mathrm{النقطة} \mathrm{نفس} \mathrm{من} \mathrm{مرسومان} \mathrm{وهما} \overline{CD}=\overline{AB}$

---

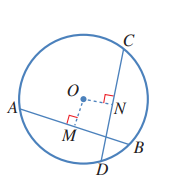
أتحقق من فهمي صفحة 41

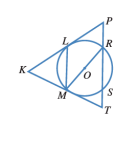
في الشكل المجاور، $\overrightarrow{TQ} و \overrightarrow{TP}$ مماسان لدائرة مركزها O: 

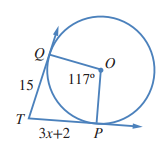
a) أجد قيمة x   

 $3x + 2=15\to x=\frac{13}{3}$

b) أجد قياس الزاوية PTQ

 $\mathrm{القطر} \mathrm{نصف} \mathrm{مع} \mathrm{مماسية} \mathrm{لانها} \measuredangle OPT=90° ,\measuredangle OQT=90°$

$\mathrm{بالتالي} 360°\mathrm{يساوي} \mathrm{الرباعي} \mathrm{الشكل} \mathrm{زوايا} \mathrm{مجموع}$

$\measuredangle OPT=360-(90+90+117)=63°$

---

اتحقق من فهمي صفحة 42

برج مراقبة: تبعد أقصى نقطة يمكن مشاهدتها من قمة برج مراقبة مسافة 32km عنه. ما ارتفاع قمة البرج عن سطح الأرض، بافترض أن الأرض كرة طول نصف قطرها 6400km تقريبا 

$A{B}^2=B{C}^2+A{C}^2$

${\left(6400+32\right)}^2={\left(6400\right)}^2+A{C}^2$

$41370624=40960000+A{C}^2$

$A{C}^2=410624\Rightarrow AC\approx 640.8$

---

أتدرب وأحل المسائل صفحة 42

يمثل الشكل المجاور دائرة مركزها O. اسمي:      

1) نصفي قطرين    $\overline{OR} ,\overline{OM}$

2) وترين                 $\overline{LM} , \overline{MR}$

3) مماسين            $\overline{PK} , \overline{TK}$

4) قاطعا                   $\overline{PT}$

$\overline{CD}و \overline{AB}$ وتران لهما الطول نفسه في دائرة مركزها O: 

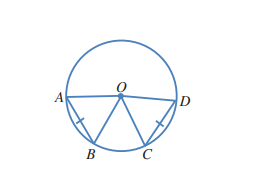
5) ما نوع المثلث AOB؟ أبرر إجابتي  

نوع المثلث AOB مثلث متساوي الساقين لأن فيه ضلعان هما نصف قطر وهما OA و OB 

6) هل المثلثان AOB و COD متطابقان؟ أبرر إجابتي 

$\mathrm{السبب،} \mathrm{متطابقان} \mathrm{المثلثان} \mathrm{نعم}$

$\mathrm{اقطار} \mathrm{انصاف} \overline{OA}=\overline{OD}$

$\mathrm{اقطار} \mathrm{انصاف} \overline{OB}=\overline{OC}$

$\mathrm{المعطيات}\mathrm{من} \overline{AB}=\overline{CD}$

$\mathrm{اضلاع} \mathrm{ثلاثة} \mathrm{بتساوي} \mathrm{المثلثان} \mathrm{يتطابق} \Leftarrow$

7) إذا كان قياس الزاوية OAB هو $65°$، فما قياس الزاوية COD؟ 

$\mathrm{متطابقان} \mathrm{المثلثان}$

$\mathrm{القياس} \mathrm{في} \mathrm{متساوية} \mathrm{المتناظرة} \mathrm{الزاويا} \Leftarrow$

$\mathrm{الساقين} \mathrm{متساوي} OAB \mathrm{المثلث} \mathrm{ايضا}$

$\mathrm{الزاوية} \mathrm{بالتالي} 65°=OBD \mathrm{الزاوية} \Leftarrow \mathrm{متساوية} \mathrm{القاعدة} \mathrm{زوايا} \Leftarrow$

$<AOB=180-\left(130\right)=150$

$<COD=50°\Leftarrow AOB \mathrm{الزاوية} \mathrm{تناظر} COD \mathrm{والزاوية}$

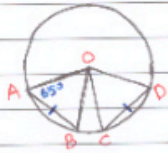
8) في الشكل المجاور، $\overline{CB}و \overline{AB}$ وتران متبقان في دائرة مركزها O.إذا كان $OD=3x-7و، OE=x+9$ فما قيمة x؟ 

$\mathrm{فهما} \mathrm{متطابقان} \overline{CB} , \overline{AB} \mathrm{الوتران} \mathrm{ان} \mathrm{بما}$

$\mathrm{متساوي} \mathrm{المركز} \mathrm{عن} \mathrm{بعداهما} \mathrm{بالتالي} \mathrm{الطول} \mathrm{في} \mathrm{متساويان}$

$OE=OD \Leftarrow$

$\Rightarrow x+9=3x-7$

$7+9=3x-x$

$16=2x\Rightarrow x=\frac{16}{2}=8$

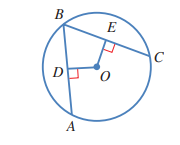
في الشكل المجاور، $\overline{EF}$ وتر في دائرة مركزها O، والنقطة M هي منتصف الوتر $\overline{EF}$: 

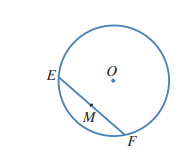
9) هل المثلثان EOM، و FOM متطابقان؟ أبرر إجابتي 

$\overline{EM}=\overline{MF} \mathrm{فان} \overline{EF} \mathrm{الوتر} \mathrm{منتصف} \mathrm{هي} M \mathrm{ان} \mathrm{بما}$

$\mathrm{لان} \mathrm{متطابقان} \mathrm{المثلثان} \mathrm{نعم}$

$\mathrm{اقطار} \mathrm{انصاف} \overline{OF}=\overline{OE}$

$\mathrm{المعطيات} \mathrm{من} MF=EM$

$\mathrm{مشترك} \mathrm{ضلع} OM$

$\mathrm{اضلاع} \mathrm{ثلاثة} \mathrm{تطابق} \mathrm{حالة} \mathrm{في} \mathrm{المثلثان} \mathrm{يتطابق} \Leftarrow$

10) هل الزاوية EOM قائمة؟ أبرر إجابتي 

نعم الزاوية EMO قائمة لأنه 

الخط الواصل بين مركز الدائرة ومنتصف الوتر يكون عموديا على الوتر  

11) إذا كان قياس الزاوية MOF هو $72°$، فما قياس الزاوية MEO؟ أبرر إجابتي 

$\Leftarrow \mathrm{متطابقان} \mathrm{المثلثان}$

$\mathrm{متساوية} \mathrm{المتناظرة} \mathrm{الزوايا}$

$<MOE=72° \Leftarrow$

$90° \mathrm{وتساوي} \mathrm{قائمة} OME \mathrm{الزاوية} \mathrm{ايضا}$

$\Rightarrow <MEO=180-(90+72)$

$=180-\left(162\right)=18°$

$180° \mathrm{يساوي} \mathrm{المثلث} \mathrm{زاويا} \mathrm{مجموع} \mathrm{حيث}$

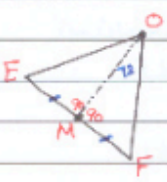
في الشكل المجاور، $\overrightarrow{PY }و \overrightarrow{PX }$ مماسان لدائرة مركزها O: 

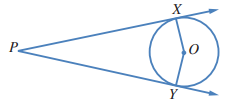
12) هل قياس الزاوية PXO هو $90°$؟ أبرر إجابتي 

نعم قياس الزاوية PXO هو $90°$ لأن الزاوية بين المماس ونصف القطر دائما قائمة  ( نصف القطر عمودي على المماس  في نقطة التماس )

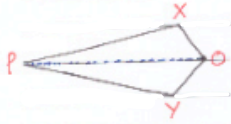
13) أبين أن المثلثين XPO و YPO متطابقان 

$\mathrm{من} \mathrm{مرسومان} \mathrm{مماسان} \overrightarrow{PX}=\overrightarrow{PY}$

$\mathrm{النقطة} \mathrm{نفس}$

$\mathrm{اقطار} \mathrm{انصاف} \overline{OX}=\overline{OY}$

$\mathrm{مشترك} \mathrm{ضلع} \overline{OP}$

$\mathrm{اضلاع} \mathrm{ثلاثة} \mathrm{يتساوي} \mathrm{المثلثان} \mathrm{يتطابق} \Leftarrow$

14) إذا كان قياس الزاوية XPO هو $17°$، فما قياس الزاوية XOY؟ 

$XOY \mathrm{الزاوية} \mathrm{قياس} \mathrm{المطلوب} 17° \mathrm{هو} XPO \mathrm{الزاوية} \mathrm{قياس}$

$OP \mathrm{نصل}$

$<XPO=17°$

$<OXP=90°$

$\Rightarrow <XOP=180-(17+90)=180-107=73°$

$\Rightarrow <XOY=2\times 73=146°$

15) في الشكل المجاور، $\overline{AB}$ وتر طوله 6cm في دائرها O. إذا كان قياس الزاوية ACO هو $90°$، و OC=4cm ، فما طول نصف قطر الدائرة؟ 

$AB=6cm,\overline{OC}=4cm$

$m<ACO=90°$

$\mathrm{الدائرة} \mathrm{قطر} \mathrm{نصف} \mathrm{طول} :\mathrm{المطلوب}$

$\mathrm{الدائرة} \mathrm{قطر} \mathrm{نصف} \mathrm{وهو} \overline{OB} \mathrm{نصل}$

$\overline{AB} \mathrm{الوتر} \mathrm{على} \mathrm{عمودي} \overline{OC} \mathrm{ان}$

$AB \mathrm{منتصف} \mathrm{هي} C\Leftarrow$

$\overline{CB}=3cm \Leftarrow \hspace{0.17em}$

${\left(\overline{OB}\right)}^2=4^2+3^2=16+9=25$

$\to \overline{OB}=\sqrt{25}=5cm$

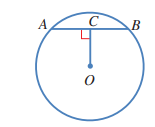
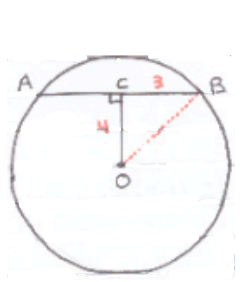
16) أحل المسألة الواردة في بداية الدرس 

في حديقة منزل عبير طاولة دائرية، وهي تريد عمل فتحة عند مركزها لتثبيت عمود يحمل مظلة بها. كيف يمكن لعبير تحديد مركز الطاولة؟ 

1- نرسم وتر في الدائرة 

2- ننصف الوتر ونرسم من نقطة المنتصف خط عمودي علىالوتر 

3- نرسم وتر ثاني في الدائرة 

4- ننصف الوتر الثاني ونرسم من نقطة المنتصف خط عمودي على الوتر 

5- ان نقطة التقاء العمودين هي مركز الطاولة 

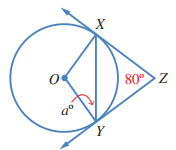
17) في الشكل المجاور، $\overrightarrow{ZY }و \overrightarrow{ZX}$ مماسان لدائرة مركزها O. أجد قيمة a

$\overline{oz} \mathrm{نصل}$

$\measuredangle xzo=40° xzy\mathrm{الزاوية} \mathrm{نصف} \mathrm{لانها}$

$\measuredangle oxz=90° \mathrm{قطر} \mathrm{نصف} \mathrm{مع} \mathrm{مماسية}$

$\Rightarrow \measuredangle xoz=50° \mathrm{المثلث} \mathrm{زوايا} \mathrm{مجموع} \mathrm{من}$

$\Rightarrow \measuredangle xoy=100° xoz \mathrm{الزاوية} \mathrm{ضعف}$

$\mathrm{متساوية} \mathrm{القاعدة} \mathrm{زوايا} \mathrm{فان} \mathrm{الضلعين} \mathrm{متطابق} oxy \mathrm{المثلث} \mathrm{ان} \mathrm{بما}$

$\Rightarrow 80° = \mathrm{القاعدة} \mathrm{زاويتي} \mathrm{قياس}$

$\Rightarrow 40°\mathrm{هي} oxy \mathrm{في} \mathrm{القاعدة} \mathrm{زاويتي} \mathrm{احدى} \mathrm{وهي} a \mathrm{قيمة}$

يظهر في كل من الشكلين الآتيين مماس لدائرة مركزها O. أجد قيمة x و y في كل حالة

$18) \measuredangle OZY=90° \mathrm{قطر} \mathrm{نصف} \mathrm{مع} \mathrm{مماس}$

$\measuredangle OZR=X=90-78=12°$

$y=180-(12+12)=180-24=156°$

 

$19) \measuredangle OZR=50°$

$\mathrm{متساوية} \mathrm{القاعدة} \mathrm{زوايا} \mathrm{وبالتالي} \mathrm{اقطار} \mathrm{انصاف} OZ,OR \mathrm{حيث} \mathrm{الضلعين} \mathrm{متطابق} OZR \mathrm{المثلث} \mathrm{لان}$

$\measuredangle OZF=90°\mathrm{قطر} \mathrm{نصف} \mathrm{مع} \mathrm{مماسية}$

$y=90-50=40°$

$X=180-( 50+50)=80°$

20) في الشكل المجاور، $\overleftrightarrow{AB }$ مماس لدائرة مركزها O في النقطة C. لماذا يعد المثلث BCD متطابق الضلعين؟ أبرر إجابتي 

 

 

$\mathrm{اقطار} \mathrm{انصاف} OC , OD \mathrm{لان} \mathrm{الضلعين} \mathrm{متطابق} COD \mathrm{المثلث} \mathrm{الان}$

$\Rightarrow \measuredangle OCD=\frac{180-64}{2}=58°$

$\measuredangle OCB=90° \mathrm{قطر} \mathrm{نصف} \mathrm{مع} \mathrm{مماس}$

$\measuredangle DCB=90-58=32°$

$\Rightarrow \mathrm{الضلعين} \mathrm{متطابق} \mathrm{المثلث} \mathrm{لذلك} \mathrm{متساويان} \mathrm{القاعدة} \mathrm{زاويتي} BCD\mathrm{المثلث} \mathrm{في}$

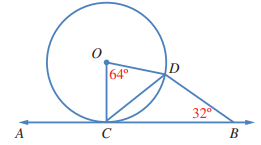
21) كم مماسا يمكن أن يرسم للدائرة من نقطة عليها، ومن نقطة خارجها، ومن نقطة داخلها؟ أبرر إجابتي 

من نقطة عليها : مماسا واحدا

من نقطة خارجها: مماسان

من نقطة داخلها : لايمكن رسم اي مماس يعني صفر

مهارات التفكير العليا 

22) تحد: $\overline{AB}$ وتر مشترك بين دائرتين متقاطعتين، وهو عمودي على القطعة المستقيمة $\overline{ON}$  الواصلة بين مركزهما. إذا كان AB=14cm ، فما طول $\overline{ON }$؟ أبرر إجابتي 

 

$\overline{AP} =7cm\Leftarrow \mathrm{ينصفه} \mathrm{بالتالي} AB \mathrm{الوتر} \mathrm{يعامد} NP$

${\left(AN\right)}^2={\left(PN\right)}^2+{\left(AP\right)}^2$

${12}^2={\left(PN\right)}^2+7^2\Rightarrow {\left(PN\right)}^2=95\Rightarrow PN=\sqrt[]{95}\Rightarrow PN\approx 9.75$

${\left(AO\right)}^2={\left(OP\right)}^2+{\left(AP\right)}^2\Rightarrow {18}^2={\left(OP\right)}^2+7^2\Rightarrow {\left(OP\right)}^2=275$

$\Rightarrow OP=\sqrt[]{275}\approx 16.58$

$\Rightarrow \overline{ON}=\overline{OP} +\overline{PN}$

$=16.58+9.75=26.33cm\mathrm{تقريب}$

 

 

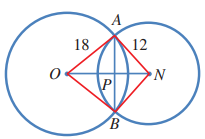
23) برهان: $\overline{CD} و \overline{AB}$ وتران متساويان في دائرة مركزها N. أثبت أن لهما البعد نفسه عن النقطة N  

 

$ON=OP \mathrm{ان} \mathrm{نثبت} \mathrm{ان} \mathrm{نريد}$

$ON=OP \mathrm{يكون} \mathrm{بالتالي} \mathrm{متطابقان} ODN,OBP \mathrm{المثلثين} \mathrm{ان} \mathrm{سنثبت}$

$OB=OD ,OB=ND\mathrm{اقطار} \mathrm{انصاف}$

$CD=AB \Rightarrow \mathrm{الوترين} \mathrm{ينصفان} ON,OP \mathrm{بالتالي} \mathrm{الوتر} \mathrm{على} \mathrm{عمودي} \mathrm{يكون} \mathrm{والبعد}$

$\Rightarrow \mathrm{متساويان} \mathrm{هما} \mathrm{المتساويين} \mathrm{الوترين} \mathrm{انصاف}$

$\mathrm{قائمان} \mathrm{المثلثان} \mathrm{ان} \mathrm{بما} و\Rightarrow \mathrm{ووتر} \mathrm{ضلع} \mathrm{تساوي} \mathrm{في} \mathrm{المثلثين} \mathrm{يتطابق}$

$\Rightarrow OP=ON\mathrm{المثلثان} \mathrm{تطابق} \mathrm{بسبب}$         

 

 

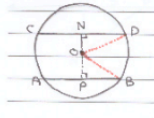
24) تبرير: $\overleftrightarrow{AB }$ مماس لدائرة مركزها N في النقطة A، وطول نصف قطرها 3cm، و BA=5cm. قالت سارة إن BN=4cm؛ لأن ${\left(BN\right)}^2={\left(BA\right)}^2-{\left(AN\right)}^2=16$. هل قول سارة صحيح؟ أبرر إجابتي 

$3cm=\mathrm{القطر} \mathrm{نصف}$

$BA=5cm$

$\Leftarrow \mathrm{لان} \mathrm{خطا} \mathrm{هو} BN=4 \mathrm{ان} \mathrm{سارة} \mathrm{قول}$

${\left(BN\right)}^2={\left(BA\right)}^2+{\left(AN\right)}^2=5^2+3^2=34$

$\Rightarrow BN=\sqrt[]{34}$

---

كتاب التمارين صفحة 20

يمثل N مركز الدائرة في الشكل المجاور . اذا كان $JK=LM=24cm$، وكان $NP=9cm$،فاجد: 

 

1) طول $\overline{NQ}$     $NQ=NP=9cm$

2) طول نصف قطر الدائرة    

$PK=\frac{1}{2}JK=12$

${\left(NK\right)}^2={\left(12\right)}^2+{\left(9\right)}^2=144+81=225$

$NK=\sqrt[]{225}=15cm$

$\overline{SA} و، \overline{SB}$ مماسان لدائرة مركزها Q. اذا كان طول نصف قطر الدائرة $10cm$، فاجد: 

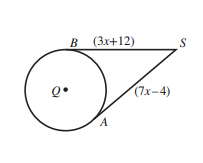
3) قيمة x

$3x+12=7x-4\to x=4$

4) طول $\overline{QS}$

${\left(QS\right)}^{2^{}}={\left(10\right)}^2+{\left(24\right)}^2=100+576=676$

$QS=\sqrt[]{676}=26cm$

$\overline{MA} و،\overline{MB}$ مماسان لدائرة مركزها N. اذا كان $MN=34cm$، فاجد: 

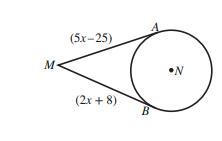
5) قيمة x 

$5x-25=2x+8\to x=11$

6) طول نصف قطر الدائرة 

${\left(34\right)}^2={\left(30\right)}^2+{\left(NA\right)}^2$

$1156=900+{\left(NA\right)}^2$

$1156-900=256={\left(NA\right)}^2$

$NA=16cm$

7) يبين الشكل المجاور مماسا لدائرة مركزها O. اجد قيمة كل من x،و y 

 

$180-52=128°$

$y=\frac{128}{2}64°$

$52+90+x=180$

$x=180-142=38°$

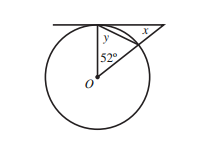
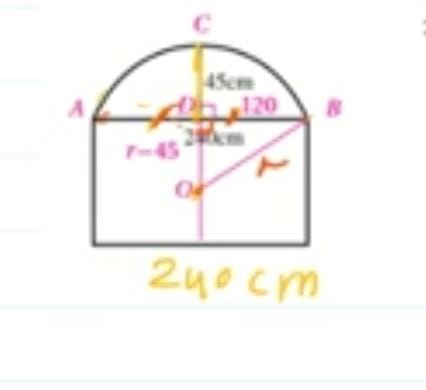
نافذة على شكل مستطيل طولها 240cm، يعلو المستطيل قوس من دائرة كما في الشكل المجاور. اذا كان ارتفاع منتصف القوس عن منتصف الضلع العلوي من المستطيل 45cm، فاجد: 

 

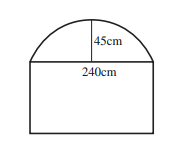
8) طول نصف قطر الدائرة التي كان القوس جزءا منها 

$r^2={\left(120\right)}^2+{(r-45)}^2$

$r^2=14400+r^2-2x45xr+{\left(45\right)}^2$

$14400-90r+2025=0$

$r=182.5cm$