رياضيات فصل أول

تحليلُ ثلاثياتِ الحدودِ ${\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathit{b}\mathit{x}\mathbf{+}\mathit{c}$
 

تهيئة  :

عندَ ضربِ مقدارَينِ جبريَّينِ، فإنَّ كلاً منهُما يكونُ عاملاً لناتجِ الضربِ.

$$\begin{gathered} \mathbf{(}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{2}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{3}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{x}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{3}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{2}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{2}\mathbf{*}\mathbf{3} \\ \mathbf{=}\mathbf{ }{\mathit{x}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{(}\mathbf{3}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{2}\mathbf{)}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{6} \\ \mathbf{=}\mathbf{ }{\mathit{x}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{5}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{6} \end{gathered}$$

نلاحظ النمط : 

$$\begin{gathered} \mathbf{(}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{2}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{3}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }{\mathit{x}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{(}\mathbf{3}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{2}\mathbf{)}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{2}\mathbf{*}\mathbf{3} \\ \mathbf{(}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{m}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{n}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathbf{ }\mathbf{(}\mathit{n}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{m}\mathbf{)}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{m}\mathit{n} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}{\mathit{x}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{ }\mathbf{ }\mathit{b}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{c} \end{gathered}$$

 

باختصار:  معامل الحد الأوسط يساوي مجموع n  و m  ، والحد الأخير يساوي ناتج ضرب m و n .

ملاحظة مهمة : إذا كانت إشارة الحد الأخير  موجبة فإن  لـ  m و n  نفس الإشارة (سواء موجبة أو سالبة) ويعتمد تحديد الإشارة على إشارة الحد الأوسط .

---

مثال 1 : أحلل ${\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathbf{7}\mathit{x}\mathbf{+}\mathbf{12}$ .

 

الحل : 

لاحظ أن إشارة الحد الثابت (الأخير) موجبة وبالتالي فإن للعددين نفس الإشارة ، وبما أن معامل الحد الأوسط موجب فإن إشارة العددين موجبة

الآن  نفكر في عددين مجموعهما 7 وحاصل ضربهما 12 .

ولتسهيل وتقليل الاحتمالات الممكنة نفكر أولاً  بعددين حاصل ضربهما 12  ـ ثم نختبر مجموعهما ليحقق شرط المجموع : وإليك التوضيح :

وبما أننا اخترنا , 3 , 4  فإن الناتج سيكون : 

${\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathbf{7}\mathit{x}\mathbf{+}\mathbf{12}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathit{x}\mathbf{+}\mathbf{3}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{+}\mathbf{4}\mathbf{)}$

 

وللتحقق نضرب القوسين ببعضهما مستخدمين خاصية التوزيع كالتالي :

$$\begin{gathered} \mathbf{ }\mathbf{(}\mathit{x}\mathbf{+}\mathbf{3}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{+}\mathbf{4}\mathbf{)}\mathbf{ }\mathbf{=}{\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathbf{4}\mathit{x}\mathbf{+}\mathbf{3}\mathit{x}\mathbf{+}\mathbf{12} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}{\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathbf{7}\mathit{x}\mathbf{+}\mathbf{12} \end{gathered}$$

---

مثال 1 : أحلل ${\mathit{x}}^{\mathbf{2}}\mathbf{-}\mathbf{10}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{16}$ .

الحل :

لاحظ أن إشارة الحد الثابت (الأخير) موجبة وبالتالي فإن للعددين نفس الإشارة ، وبما أن معامل الحد الأوسط سالب فإن إشارة العددين سالبة

الآن  نفكر في عددين مجموعهما 10- وناتج ضربهما 16+  وإليك التوضيح :

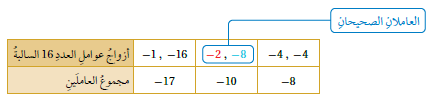
وبما أننا اخترنا  8-  , 2- فإن الناتج سيكون : 

${\mathit{x}}^{\mathbf{2}}\mathbf{-}\mathbf{10}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{16}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathit{x}\mathbf{-}\mathbf{2}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{-}\mathbf{8}\mathbf{)}$

وللتحقق نضرب القوسين ببعضهما مستخدمين خاصية التوزيع كالتالي :

$$\begin{gathered} \mathbf{(}\mathit{x}\mathbf{-}\mathbf{2}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{-}\mathbf{8}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{=}{\mathit{x}}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathit{x}\mathbf{-}\mathbf{8}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{16}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}{\mathit{x}}^{\mathbf{2}}\mathbf{-}\mathbf{10}\mathit{x}\mathbf{ }\mathbf{+}\mathbf{16}\mathbf{ } \end{gathered}$$

---

ملاحظة مهمة : إذا كانت إشارة الحد الأخير  سالبة فإن  لـ  m و n  إشارتين مختلفتين ويعتمد تحديد الإشارة على إشارة الحد الأوسط ،

---

مثال 3 : أحلل:    ${\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathit{x}\mathbf{ }\mathbf{-}\mathbf{20}$ .

 

الحل :

لاحظ أن إشارة الحد الثابت (الأخير) سالبة وبالتالي فإن للعددين إشارتين مختلفتين  ، وبما أن  إشارة معامل الحد الأوسط موجبة  فهذا يعني أن مجموع العددين موجب $\mathbf{\Leftarrow }$ ( العدد الكبير هو العدد الموجب في هذه الحالة )

 

الآن  نفكر في عددين مختلفين في الإشارة مجموعهما 1+ وناتج ضربهما 20-  وإليك التوضيح :

 

 

 

 

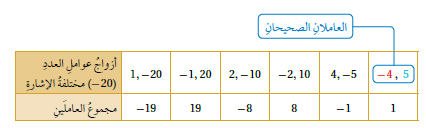
وبما أننا اخترنا  4-  , 5 فإن الناتج سيكون : 

${\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathit{x}\mathbf{ }\mathbf{-}\mathbf{20}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathit{x}\mathbf{+}\mathbf{5}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{-}\mathbf{4}\mathbf{)}$

وللتحقق نضرب القوسين ببعضهما مستخدمين خاصية التوزيع كالتالي :

$$\begin{gathered} \mathbf{ }\mathbf{(}\mathit{x}\mathbf{+}\mathbf{5}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{-}\mathbf{4}\mathbf{)}\mathbf{ }\mathbf{=}{\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathbf{5}\mathit{x}\mathbf{-}\mathbf{4}\mathit{x}\mathbf{ }\mathbf{-}\mathbf{20} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathit{x}\mathbf{ }\mathbf{-}\mathbf{20}\mathbf{ } \end{gathered}$$

---

مثال 4: منَ الحياةِ 

يمثلُ ثلاثيُّ الحدودِ ${\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathbf{9}\mathit{x}\mathbf{+}\mathbf{18}$ مساحةَ مرآةٍ مستطيلةِ الشكلِ بالمترِ المربعِ. إذا كانَ عرضُ المرآة $\mathbf{(}\mathit{x}\mathbf{+}\mathbf{3}\mathbf{)}$ مترًا، فأجدُ كلًّ مِنْ طولِها ومحيطِها بدلالةِ x

الحل : 

بما أن المرآة مستطيلة الشكل ، ومن المعلوم أن مساحة المستطيل  تساوي (الطول * العرض)

وبما أننا نعلم العرض وعندنا المساحة ، إذاً يمكننا إيجاد الطول بسهولة كالتالي:

$$\begin{gathered} \mathit{A}\mathbf{=}\mathit{L}\mathbf{*}\mathit{W} \\ {\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathbf{9}\mathit{x}\mathbf{+}\mathbf{18}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{L}\mathbf{*}\mathbf{ }\mathbf{(}\mathit{x}\mathbf{+}\mathbf{3}\mathbf{)} \\ \mathbf{(}\mathit{x}\mathbf{+}\mathbf{3}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{+}\mathbf{6}\mathbf{)}\mathbf{=}\mathit{L}\mathbf{*}\mathbf{ }\mathbf{(}\mathit{x}\mathbf{+}\mathbf{3}\mathbf{)} \\ \frac{\cancel{\mathbf{(}\mathbf{x}\mathbf{+}\mathbf{3}}\mathbf{\left)}\mathbf{\right(}\mathbf{x}\mathbf{+}\mathbf{6}\mathbf{)}}{\cancel{\mathbf{(}\mathbf{x}\mathbf{+}\mathbf{3}\mathbf{)}}}\mathbf{ }\mathbf{=}\frac{\mathbf{L}\mathbf{*}\mathbf{ }\cancel{\mathbf{(}\mathbf{x}\mathbf{+}\mathbf{3}\mathbf{)}}}{\mathbf{ }\cancel{\mathbf{(}\mathbf{x}\mathbf{+}\mathbf{3}\mathbf{)}}} \\ \mathit{x}\mathbf{+}\mathbf{6}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{L} \end{gathered}$$

الآن نجد المحيط وهو مجموع أطوال أضلاع المرآة .

$$\begin{gathered} \mathit{p}\mathbf{=}\mathbf{ }\mathbf{2}\mathit{l}\mathbf{+}\mathbf{2}\mathit{w} \\ \mathbf{ }\mathbf{ }\mathbf{=}\mathbf{2}\mathbf{(}\mathit{x}\mathbf{+}\mathbf{6}\mathbf{)}\mathbf{+}\mathbf{2}\mathbf{(}\mathit{x}\mathbf{+}\mathbf{3}\mathbf{)} \\ \mathbf{ }\mathbf{ }\mathbf{=}\mathbf{2}\mathit{x}\mathbf{+}\mathbf{12}\mathbf{+}\mathbf{2}\mathit{x}\mathbf{+}\mathbf{6} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{4}\mathit{x}\mathbf{+}\mathbf{18} \end{gathered}$$

---