تصنيف المثلثات حسب قياسات زواياها
فكرة الدرس : أصنف المثلثات حسب قياسات زواياها.
•• يوجد في أي مثلث زاويتان حادتان على الأقل، ويُصنف المثلث حسب الزاوية الثالثة ، كما يأتي :
 |
 |
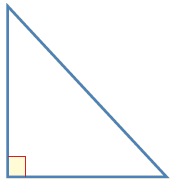 |
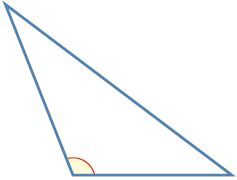
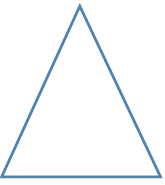
| مثلث منفرج الزاوية | مثلث حاد الزوايا | مثلث قائم الزاوية |
|
إحدى زواياه منفرجة والزاويتان الأخريان حادتان. |
زواياه الثلاث حادة. |
إحدى زواياه قائمة والزاويتان الأخريان حادتان.
|
مثال :
أصنف كل من المثلثات الآتية حسب قياسات زواياها، وأبرر إجابتي :
|
المثلث منفرج الزاوية ؛ لأن إحدى زواياه منفرجة ، والزاويتان الأخريان حادتان. |
 |
1) |
| المثلث حاد الزوايا ؛ لأن زواياه الثلاث حادة. | 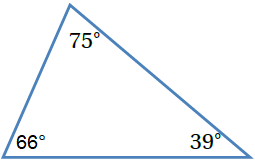 |
2) |
| المثلث قائم الزاوية ؛ لأن إحدى زواياه قائمة، والزاويتان الأخريان حادتان. | 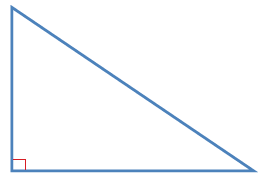 |
3) |
•• مجموع قياسات زوايا أي مثلث يساوي .
ويُمكن استعمال هذه الحقيقة في إيجاد قياس زاوية مجهولة في مثلث ثم تصنيفه حسب قياسات زواياه :
مثال :
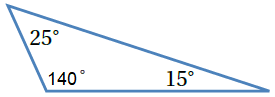
أصنف كل من المثلثات الآتية حسب قياسات زواياها ، وأبرر إجابتي :
 |
c) | 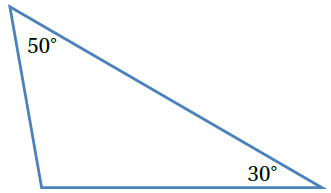 |
b) | 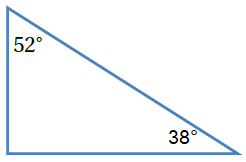 |
a) |
الحل :
|
الخطوة 1 : أجد قياس الزاوية الثالثة أفترض أن قياس الزاوية المجهولة |
a) |
|
مجموع قياسات زوايا المثلث = |
|
|
أجمع و |
|
|
أستعمل العلاقة بين الجمع والطرح |
|
|
أكتب ناتج الطرح |
الخطوة 2 : أصنف المثلث
بما أنّ المثلث يحوي زاوية قائمة ؛ إّذن : المثلث قائم الزاوية .
|
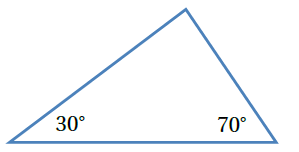
الخطوة 1 : أجد قياس الزاوية الثالثة أفترض أن قياس الزاوية المجهولة |
b) |
| مجموع قياسات زوايا المثلث = | |
| أجمع و | |
| أستعمل العلاقة بين الجمع والطرح | |
| أكتب ناتج الطرح |
الخطوة 2 : أصنف المثلث
بما أنّ المثلث يحوي زاوية قياسها وهي زاوية منفرجة ؛ إّذن : المثلث منفرج الزاوية .
|
الخطوة 1 : أجد قياس الزاوية الثالثة أفترض أن قياس الزاوية المجهولة |
c) |
| مجموع قياسات زوايا المثلث = | |
| أجمع و | |
| أستعمل العلاقة بين الجمع والطرح | |
| أكتب ناتج الطرح |
الخطوة 2 : أصنف المثلث
بما أنّ زوايا المثلث جميعها حادة ، إذن : المثلث حاد الزوايا.