الرياضيات فصل أول

الدرس الثالث: تطبيقات القيم القصوى

سنتعرف في درس تطبيقات القيم القصوى إلى:

1. القيمة العظمى المحلية.
2. القيمة الصغرى المحلية.
3. اختبار المشتقة الثانية لتصنيف القيم القصوى.
4. استراتيجية حل مسائل القيم القصوى.
5. إيجاد أكبر مساحة ممكنة.
6. إيجاد أقل كمية ممكنة.
7. إيجاد أكبر حجم ممكن.
8. تطبيقات اقتصادية (التكلفة، التكلفة الحدية، الإيراد، الإيراد الحدي، الربح، الربح الحدي).

 

•  تعلمت سابقاً أنه إذا كانت $x=a$  ضمن مجال الاقتران $f\left(x\right)$، فإن القيمة $a$ تسمى قيمة حرجة للاقتران $f\left(x\right)$ ، إذا كانت $f\text{'}\left(a\right)=0$ ،وتسمى النقطة $\left(a, f\left(a\right)\right)$ نقطة حرجة للاقتران.

• كما تعلمت سابقاً أن النقط الحرجة يكون عندها المماس أفقياً يوازي محور $x$.

• تعلمت أيضاً أنه لإيجاد النقط الحرجة للاقتران $f\left(x\right)$ ، نضع  $f\text{'}\left(x\right)=0$.

 

مثال1: أجد النقط الحرجة للاقتران: $f\left(x\right)=x^3-3x+5$.

الحل:

الاقتران المعطى	$f\left(x\right)=x^3-3x+5$
اشتق الاقتران	$f\text{'}\left(x\right)=3x^2-3$
نضع    $f\text{'}\left(x\right)=0$	$3x^2-3=0$
بقسمة المعادلة على $3$	$x^2-1=0$
بتحليل المعادلة	$\left(x-1\right)\left(x+1\right)=0$
باستخدام خاصية الضرب الصفري	$x-1=0 or x+1=0$
بحل المعادلتين	$x=1 or x=-1$
عند $x=1$   نجد   $y$ عند $x=-1$    نجد   $y$	$$\begin{gathered} y=f\left(1\right)={\left(1\right)}^3-3\left(1\right)+5 \\ =1-3+5 \\ =3 \\ y=f\left(-1\right)={\left(-1\right)}^3-3\left(-1\right)+5 \\ =-1+3+5 \\ =7 \end{gathered}$$

 إذاً، عند   $x=1 ,-1$  قيم حرجة للاقتران ، والنقط الحرجة هي: $\left(1,3\right) , \left(-1,7\right)$

 

أولًا: تصنيف القيم الحرجة باستخدام اختبار المشتقة الثانية 

تعلمت سابقاً أن النقط الحرجة تصنف إلى:

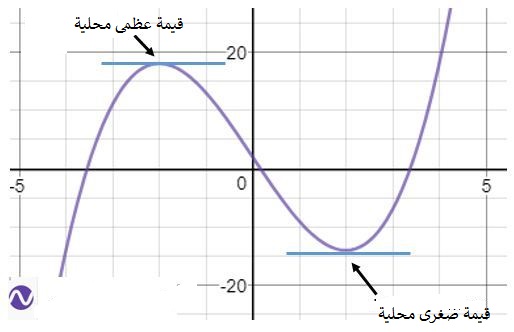• النقط العظمى المحلية: هي النقطة التي يتحول عندها منحنى الاقتران من متزايد إلى متناقص  (من اليسار إلى اليمين)، أي تتحول عندها إشارة المشتقة الأولى من موجبة إلى سالبة.
• النقطة الصغرى المحلية:هي النقطة التي يتحول عندها منحنى الاقتران من متناقص إلى متزايد (من اليسار إلى اليمين)، أي تتحول عندها المشتقة الأولى من سالبة إلى موجبة

نظرية

بافتراض وجود $f\text{'}, f\text{'}\text{'}$ لأي نقطة في فترة مفتوحة تحوي $c$ ، وأن : $f\text{'}\left(c\right)=0$، فإنه يمكن استنتاج ما يأتي:

• إذا كان : $f\text{'}\text{'}\left(c\right)<0$، فإن $f\left(c\right)$ هي قيمة عظمى محلية للاقتران $f$.
• إذا كان: $f\text{'}\text{'}\left(c\right)>0$، فإن $f\left(c\right)$ هي قيمة صغرى محلية للاقتران$f$.
• إذا كان: $f\text{'}\text{'}\left(c\right)=0$، فإن اختبار المشتقة الثانية يفشل, وفي هذه الحالة ، نلجأ إلى استخدام اختبار المشتقة الأولى لتصنيف القيم القصوى المحلية.

اختبار المشتقة الثانية لتصنيف القيم القصوى

•  أجد المشتقة الأولى للاقتران $f$، وهي: $f\text{'}\left(x\right)$.
• أضع المشتقة الأولى للاقتران تساوي صفراً، أي $f\text{'}\left(x\right)=0$.لإيجاد قيم $x=a$ الحرجة للاقتران.
• أجد المشتقة الثانية للاقتران $f$ عند a، وهي: $f\text{'}\text{'}\left(a\right)$.
• نعوض القيم الحرجة للاقتران في المشتقة الثانية

       1. فإذا كانت المشتقة الثانية موجبة يكون عندها $f\left(a\right)$ قيمة صغرى محلية.

      2.  وإذا كانت المشتقة الثانية سالبة يكون عندها $f\left(a\right)$ قيمة عظمى محلية.

 

مثال1: إذا كان: $f\left(x\right)=x^2-6x+1$، فاستعمل اختبار المشتقة الثانية لإيجاد القيم القصوى للاقتران $f$.

الحل:

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران.

الاقتران المعطى	$f\left(x\right)=x^2-6x+1$
نشتق الاقتران	$f\text{'}\left(x\right)=2x-6$
نساوي المشتقة بالصفر ، $f\text{'}\left(x\right)=0$	$2x-6=0$
بحل المعادلة من خلال إضافة $6$ لطرفي المعادلة وقسمة المعادلة على $2$ ينتج	$$\begin{gathered} 2x=6 \\ x=3 \end{gathered}$$

إذاً القيمة الحرجة للاقتران $f$ هي:$x=3$

الخطوة 2: أجد المشتقة الثانية للاقتران

اقتران المشتقة الأولى	$f\text{'}\left(x\right)=2x-6$
اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=2$

الخطوة 3: أعوض القيم الحرجة في المشتقة الثانية ؛ لتصنيفها

اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=2$
نعوض $x=3$	$f\text{'}\text{'}\left(3\right)=2>0$

بما أن $f\text{'}\text{'}\left(3\right)>0$، فإن للاقتران قيمة صغرى محلية عند $x=3$ ، وهي:  $f\left(3\right)=-8$    لأن $f\left(3\right)={\left(3\right)}^2-6\left(3\right)+1=-8$

 

مثال 2: إذا كان:   $f\left(x\right)=x^3-12x+5$، فاستعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية للاقتران$f$.

الحل:

الخطوة1: أجد المشتقة الأولى والقيم الحرجة للاقتران

الاقتران المعطى	$f\left(x\right)=x^3-12x+5$
نشتق الاقتران	$f\text{'}\left(x\right)=3x^2-12$
نساوي المشتقة بالصفر ،  $f\text{'}\left(x\right)=0$	$3x^2-12=0$
بقسمة المعادلة على $3$	$x^2-4=0$
بتحليل المعادلة	$\left(x-2\right)\left(x+2\right)=0$
باستخدام خاصية الضرب الصفري	$x-2=0 or x+2=0$
بحل المعادلتين	$x=2 or x=-2$

إذاً القيم الحرجة للاقتران $f$، هي: $x=2 , x=-2$

الخطوة 2: أجد المشتقة الثانية للاقتران

اقتران المشتقة الأولى	$f\text{'}\left(x\right)=3x^2-12$
اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=6x$

الخطوة 3: أعوض القيم الحرجة في المشتقة الثانية؛ لتصنيفها

اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=6x$
نعوض في المشتقة الثانية $x=2 , x=-2$	$$\begin{gathered} f\text{'}\text{'}\left(2\right)=6\left(2\right)=12>0 \\ f\text{'}\text{'}\left(-2\right)=6\left(-2\right)=-12<0 \end{gathered}$$

بما أن $f\text{'}\text{'}\left(2\right)>0$، فإن للاقتران $f$ قيمة صغرى محلية عند $x=2$ ، وهي: $f\left(2\right)=-11$

لأن: $f\left(2\right)={\left(2\right)}^3-12\left(2\right)+5=-11$

بما أن $f\text{'}\text{'}\left(-2\right)<0$، فإن للاقتران $f$ قيمة عظمى محلية عند $x=-2$ ، وهي: $f\left(-2\right)=21$  لأن $f\left(-2\right)={\left(-2\right)}^3-12\left(-2\right)+5=21$

 

مثال 3:إذا كان: $f\left(x\right)=2x^3-6x^2-18x+1$، فاستخدم اختبار المشتقة الثانية لإيجاد القيم القصوى للاقتران$f$.

الحل:

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران

الاقتران المعطى	$f\left(x\right)=2x^3-6x^2-18x+1$
نشتق الاقتران	$f\text{'}\left(x\right)=6x^2-12x-18$
نساوي المشتقة بالصفر ، $f\text{'}\left(x\right)=0$	$6x^2-12x-18=0$
بقسمة المعادلة على $6$	$x^2-2x-3=0$
بتحليل المعادلة	$\left(x-3\right)\left(x+1\right)=0$
باستخدام خاصية الضرب الصفري	$x-3=0 or x+1=0$
بحل المعادلتين	$x=3 or x=-1$

إذاً، القيم الحرجة للاقتران $f$، هي: $x=3 , x=-1$

الخطوة 2: أجد المشتقة الثانية

اقتران المشتقة الأولى	$f\text{'}\left(x\right)=6x^2-12x-18$
اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=12x-12$

الخطوة 3: أعوض القيم الحرجة في المشتقة الثانية؛لتصنيفها

اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=12x-12$
نعوض في المشتقة الثانية $x=3 , x=-1$	$$\begin{gathered} f\text{'}\text{'}\left(3\right)=12\left(3\right)-12=24>0 \\ f\text{'}\text{'}\left(-1\right)=12\left(-1\right)-12=-24<0 \end{gathered}$$

بما أن $f\text{'}\text{'}\left(3\right)>0$، فإن للاقتران $f$ قيمة صغرى محلية عند $x=3$ ، وهي: $f\left(3\right)=-53$ لأن $f\left(3\right)=2{\left(3\right)}^3-6{\left(3\right)}^2-18\left(3\right)+1=-53$

بما أن $f\text{'}\text{'}\left(-1\right)<0$، فإن للاقتران $f$ قيمة عظمى محلية عند $x=-1$ ، وهي: $f\left(-1\right)=11$ لأن$f\left(-1\right)=2{\left(-1\right)}^3-6{\left(-1\right)}^2-18\left(-1\right)+1=11$

 

مثال 4: إذا كان: $f\left(x\right)=x\left(x^2-27\right)$، فأستخدم اختبار المشتقة الثانية لإيجاد القيم القصوى للاقتران$f$.

الحل:

الخطوة 1: أجد المشتقة الأولى والقيم القصوى للاقتران

الاقتران المعطى	$$\begin{gathered} f\left(x\right)=x\left(x^2-27\right) \\ f\left(x\right)=x^3-27x \end{gathered}$$
نشتق الاقتران	$f\text{'}\left(x\right)=3x^2-27$
نساوي المشتقة بالصفر ، $f\text{'}\left(x\right)=0$	$3x^2-27=0$
بقسمة المعادلة على $3$	$x^2-9=0$
بتحليل المعادلة	$\left(x-3\right)\left(x+3\right)=0$
باستخدام خاصية الضرب الصفري	$x-3=0 or x+3=0$
بحل المعادلتين	$x=3 or x=-3$

إذاً، القيم الحرجة للاقتران $f$ هي: $x=3 , x=-3$

الخطوة 2: أجد المشتقة الثانية للاقتران

اقتران المشتقة الأولى	$f\text{'}\left(x\right)=3x^2-27$
اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=6x$

الخطوة 3: أعوض القيم الحرجة في المشتقة الثانية؛ لتصنيفها

اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=6x$
نعوض المشتقة الثانية  $x=3 , x=-3$	$$\begin{gathered} f\text{'}\text{'}\left(3\right)=6\left(3\right)=18>0 \\ f\text{'}\text{'}\left(-3\right)=6\left(-3\right)=-18<0 \end{gathered}$$

بما أن $f\text{'}\text{'}\left(3\right)>0$، فإن للاقتران $f$ قيمة صغرى محلية عند $x=3$ ، وهي: $f\left(3\right)=-54$ لأن   $f\left(3\right)={\left(3\right)}^3-27\left(3\right)=-54$     

 بما أن $f\text{'}\text{'}\left(-3\right)<0$، فإن للاقتران $f$ قيمة عظمى محلية عند $x=-3$ ، وهي: $f\left(-3\right)=54$$f\left(-3\right)={\left(-3\right)}^3-27\left(-3\right)=54$

 

أتحقق من فهمي

 إذا كان: $f\left(x\right)=x^3-3x^2-24x+2$، فأستعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية للاقتران $f$.                                                                                                                                         الإجابة: للاقتران $f$ قيمة صغرى محلية عند $x=4$ ، وهي: $f\left(4\right)=-78$ ، للاقتران $f$ قيمة عظمى محلية عند $x=-2$ ، وهي: $f\left(-2\right)=30$.

 

ثانيا: مسائل على القيم القصوى

استراتيجية حل المسألة

 

1)افهم المسألة: أقرا المسألة بشكل جيد ، ثم أحدد المعلومات اللازمة لحلها.

2) أرسم مخططًا: أرسم مخططًايمثل المسألة إن أمكن، ثم أدون عليه المعلومات المهمة لحل المسالة، وأختار متغيراً يمثل الكمية التي أريد أن أجد لها أكبر قيمة أو أقل قيمة ، وأختار رموزاً للمتغيرات الأخرى في المسألة ، ثم أستعمل المتغيرات لكتابة اقتران قيمته القصوى هي القيمة المطلوبة.

3) أجد القيم الحرجة للاقتران: أجد القيم التي تكون عندها مشتقة الاقتران صفرًا. 

4) أجد القيمة القصوى المطلوبة: أجد القيمة الصغرى أو العظمى المطلوبة.

تطبيقات حياتية

أ) إيجاد أكبر مساحة ممكنة لمستطيل

مثال 1:قطعة أرض مستطيلة الشكل، محيطها 400 متر . جد بعدا قطعة الأرض اللذان يجعلان مساحتها أكبر ما يمكن. 

الحل: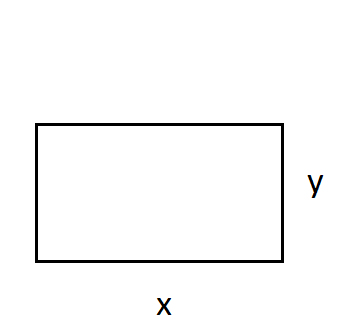      

الخطوة 1: أرسم مخططًا

​​​ أفترض أن طول قطعة الأرض $x$ ، وأن $y$ هو عرضها 

الخطوة 2: أكتب الاقتران الذي أريد إيجاد قيمته القصوى بدلالة متغير واحد.

• أجد اقتران مساحة المستطيل:                                                                      مساحة المستطيل                                          $A=xy$
• أكتب $y$  بدلالة $x$ باستعمال المحيط:  

محيط المستطيل	$p=2x+2y$
بتعويض $p=400$	$2x+2y=400$
بقسمة المعادلة على $2$	$x+y=200$
بكتابة $y$ بدلالة $x$	$y=200-x$

• أعوض $y$ بدلالة $x$ في اقتران المساحة:

  اقتران المساحة	$A=xy$
  بتعويض $y=200-x$ في اقتران المساحة	$A\left(x\right)=x\left(200-x\right)$
  بالتبسيط	$A\left(x\right)=200x-x^2$

  إذًا، الاقتران الذي يمثل مساحة قطعة الأرض هو: $A\left(x\right)=200x-x^2$

الخطوة 3: أجد القيم الحرجة للاقتران

اقتران المساحة	$A\left(x\right)=200x-x^2$
نشتق اقتران المساحة	$A\text{'}\left(x\right)=200-2x$
نساوي مشتقة اقتران المساحة بالصفر ، $A\text{'}=0$	$200-2x=0$
بحل المعادلة من خلال قسمة المعادلة على $2$ وإضافة $-100$ لطرفي المعادلة ينتج	$$\begin{gathered} 100-x=0 \\ x=100 \end{gathered}$$

إذًا، توجد قيمة حرجة عند $x=100$.

الخطوة 4: أستخدم اختبار المشتقة الثانية لتصنيف القيمة الحرجة

اقتران المشتقة الأولى مساحة	$A\text{'}\left(x\right)=200-2x$
اقتران مشتقة الثانية للمساحة	$A\text{'}\text{'}\left(x\right)=-2$

بما أن $A\text{'}\text{'}\left(x\right)<0$ لجميع قيم $x$  الموجبة ، فإنه توجد قيمة عظمى محلية عند $x=100$ ، وهذا يعني أن مساحة قطعة الأرض تكون أكبر ما يمكن عندما $x=100$ .

إذًا، طول قطعة الأرض تساوي $x=100$ متر ، وعرضها   $y=100$  متر  ،  لأن   $y=200-x=200-100=100$ 

 

مثال 2: قطعة أرض مستطيلة الشكل، يمر من أمامها نهر ، أراد صاحبها أن يسيج الجهات الثلاثة ( عدا التي يمر من أمامها النهر) بسياج طوله $600 m$ ، ما إبعاد القطعة التي تجعل مساحتها أكبر ما يمكن؟

الحل: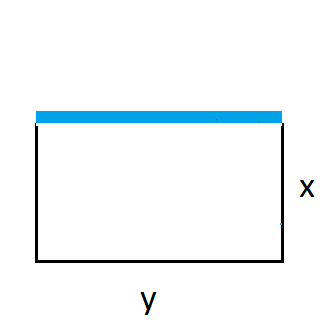

الخطوة 1: أرسم مخططًا                                    

أفترض أن طول قطعة الأرض$y$ ، وعرضها $x$   

الخطوة 2: أكتب الاقتران الذي أريد إيجاد قيمته القصوى بدلالة متغير واحد.

• أجد اقتران مساحة المستطيل: 

          مساحة المستطيل                   $A=xy$   

• أكتب $y$ بدلالة $x$ باستخدام طول السياج (المحيط)     

محيط قطعة الأرض (ما عدا الجهة الواقعة على النهر)	$p=y+2x$
لكن  $p=600$	$y+2x=600$
نكتب $y$ بدلالة $x$	$y=600-2x$

• أعوض $y=600-2x$ في اقتران المساحة

اقتران المساحة	$A=xy$
بتعويض $y=600-2x$ في اقتران المساحة	$A\left(x\right)=x\left(600-2x\right)$
بالتبسيط	$A\left(x\right)=600x-2x^2$

 إذًا، الاقتران الذي يمثل مساحة قطعة الأرض هو: $A\left(x\right)=600x-2x^2$

الخطوة 3: أجد القيم الحرجة للاقتران

اقتران المساحة	$A\left(x\right)=600x-2x^2$
نشتق اقتران المساحة	$A\text{'}\left(x\right)=600-4x$
نساوي مشتقة  اقتران المساحة بالصفر  $A\text{'}\left(x\right)=0$	$600-4x=0$
بحل المعادلة من خلال إضافة $-600$ لطرفي المعادلة وقسمة الناتج على $-4$ ينتج	$$\begin{gathered} -4x=-600 \\ x=150 \end{gathered}$$

 إذًا، توجد قيمة حرجة عند $x=150$.

الخطوة 4: أستخدم اختبار المشتقة الثانية لتصنيف القيمة الحرجة

اقتران المشتقة الأولى للمساحة	$A\text{'}\left(x\right)=600-4x$
اقتران المشتقة الثانية للمساحة	$A\text{'}\text{'}\left(x\right)=-4$

بما أن $A\text{'}\text{'}\left(x\right)<0$ لجميع قيم $x$ الموجبة ، فإنه توجد قيمة عظمى محلية عند $x=150$ ، وهذا يعني أن مساحة قطعة الأرض تكون أكبر ما يمكن عندما $x=150$.

إذًا، عرض قطعة الأرض $x$ يساوي $150 m$، وطول قطعة الأرض$y$ يساوي $300 m$ ، لأن $y=600-2x$ $y=600-2\left(150\right)=600-300=300$

 

مثال 3:صحيفة ورقية مستطيلة الشكل، مساحتها $50 c{m}^2$ ، يراد طباعة إعلان عليها. إذا كان عرض كل هامش في رأس الورقة وأسفلها $1 cm$، وفي كل جانب $0.5 cm$ ، أجد بعدي الورقة اللذين يجعلان المساحة المطبوعة أكبر ما يمكن.

الحل: 

  الخطوة 1:أرسم مخططًا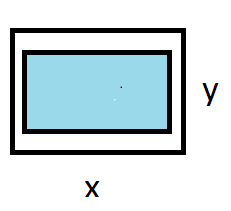 

أفرض أن طول الورقة $x$ ، وعرضها $y$

إذًا، يكون طول الورقة المطبوعة $\left(x-1\right)$ ، وعرضها $\left(y-2\right)$

الخطوة 2: أكتب الاقتران الذي أريد إيجاد قيمته القصوى بدلالة متغير واحد.

• أجد اقتران مساحة المستطيل: 

مساحة المستطيل                   $A=xy$

• أكتب $y$ بدلالة $x$ باستخدام مساحة الورق

مساحة المستطيل	$A=xy$
بتعويض  $A=50$	$xy=50$
بكتابة $y$ بدلالة $x$	$y=\frac{50}{x}$

• أعوض $y$ في اقتران المساحة المطبوعة 

اقتران المساحة المطبوعة	$A=\left(x-1\right)\left(y-2\right)$
نعوض $y=\frac{50}{x}$	$A\left(x\right)=\left(x-1\right)\left(\frac{50}{x}-2\right)$

 إذًا، الاقتران الذي يمثل المساحة المطبوعة هو: $A\left(x\right)=\left(x-1\right)\left(\frac{50}{x}-2\right)$

الخطوة 3: أجد القيم الحرجة للاقتران.

اقتران المساحة المطبوعة	$A\left(x\right)=\left(x-1\right)\left(\frac{50}{x}-2\right)$
نشتق اقتران المساحة المطبوعة باستخدام قانون مشتقة ضرب اقترانين	$A\text{'}\left(x\right)=(x-1)\left(\frac{-50}{x^2}\right)+\left(\frac{50}{x}-2\right)\left(1\right)$
بالتبسيط	$$\begin{gathered} A\text{'}\left(x\right)=\frac{-50}{x}+\frac{50}{x^2}+\frac{50}{x}-2 \\ A\text{'}\left(x\right)=\frac{50}{x^2}-2 \end{gathered}$$
نساوي مشتقة المساحة المطبوعة بالصفر  $A\text{'}\left(x\right)=0$	$\frac{50}{x^2}-2=0$
بحل المعادلة	$$\begin{gathered} \frac{50}{x^2}=2 \\ 2x^2=50 \\ {x}^2=25 \\ x=\pm 5 \end{gathered}$$

إذًا،  بما أن الطول لا يمكن أن يكون سالب ، فإن النقطه الحرجة للاقترا.ن هي:$x=5$.

الخطوة 4: أستخدم اختبار المشتقة الثانية لتصنيف القيمة الحرجة.

مشتقة اقتران المساحة المطبوعة	$A\text{'}\left(x\right)=\frac{50}{x^2}-2$
المشتقة الثانية لاقتران المساحة المطبوعة	$$\begin{gathered} A\text{'}\text{'}\left(x\right)=\frac{-50\left(2x\right)}{{\left(x^2\right)}^2}=\frac{-100x}{x^4} \\ A\text{'}\text{'}\left(x\right)=\frac{-100}{x^3} \end{gathered}$$
بتعويض $x=5$ في المشتقة الثانية	$A\text{'}\text{'}\left(5\right)=\frac{-100}{{\left(5\right)}^3}=\frac{-100}{125}<0$

إذًا، بما أن $A\text{'}\text{'}\left(5\right)<0$ ، فإن للاقتران قيمة عظمى محلية عند $x=5$ ،

أي أن المساحة المطبوعة تكون أكبر ما يمكن عندما يكون طول الصفيحة $5 cm$  ، وعرضها $10 cm$ ، لأن     $y=\frac{50}{5}=10$.

أتحقق من فهمي

أراد شخص بناء غرفة لاستقبال الضيوف في مزرعته، بحيث يكون محيط سقفها $40 m$ ، جد أكبر مساحة ممكنة لسقف الغرفة.  الإجابة:  أكبر مساحة ممكنة لسقف الغرفة $100 m^2$.

ب) إيجاد أقل كمية ممكنة

مثال 4:  نريد صنع صندوق  مفتوح من أعلى على شكل متوازي مستطيلات، قاعدته مربعة  الشكل وحجمه $32 c{m}^3$ ، جد أبعاد الصندوق التي تجعل كمية المادة المستخدمة لصنعه أقل ما يمكن.

الحل: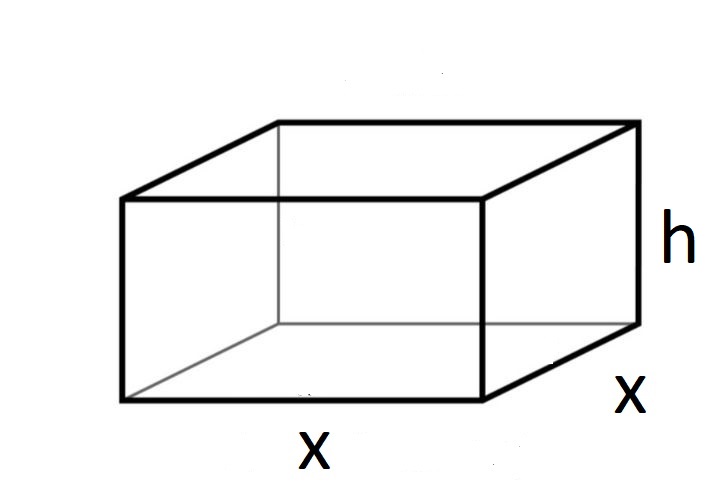 

الخطوة 1: أرسم مخططًا وأضع عليه المتغيرات

أفرض أن طول قاعدة الصندوق $x$ ، وعرضها $x$ وارتفاعه $h$ ، كما هو موضح في الشكل المجاور

الخطوة 2: أكتب الاقتران الذي أريد إيجاد قيمته القصوى بدلالة متغير واحد.

• أجد اقتران كمية المادة المستخدمة 

 كمية المادة المستخدمة في صنع الصندوق هي: المساحة الجانبية للصندوق+مساحة القاعدة

         حجم متوازي المستطيلات يساوي طول القاعدة x عرض القاعدة x الارتفاع                                          حجم الصندوق                                      $$\begin{gathered} v=L\times w\times h \\ =x\times x\times h \\ =x^{2}h \end{gathered}$$

• أكتب $h$ بدلالة $x$ باستعمال حجم الصندوق

حجم الصندوق	$v=x^{2}h$
حجم الصندوق يساوي $32$	$x^{2}h=32$
نكتب $h$ بدلالة $x$	$h=\frac{32}{x^2}$

•  أعوض $h$ في اقتران كمية المادة

أقتران  كمية المادة	$A=4xh+x^2$
بتعويض $h=\frac{32}{x^2}$	$A\left(x\right)=4x\left(\frac{32}{x^2}\right)+x^2$
بالتبسيط	$A\left(x\right)=\frac{128}{x}+x^2$

  إذًا، اقتران كمية المادة المستخدمة هو: $A\left(x\right)=\frac{128}{x}+x^2$     

الخطوة 4: أجد القيم الحرجة للاقتران

اقتران كمية المادة	$A\left(x\right)=\frac{128}{x}+x^2$
نشتق الاقتران	$A\text{'}\left(x\right)=\frac{-128}{x^2}+2x$
نساوي المشتقة بالصفر   $A\text{'}\left(x\right)=0$	$\frac{-128}{x^2}+2x=0$
بالتبسيط من خلال إضافة $\frac{128}{x^2}$ لطرفي المعادلة والضرب التبادلي ، والقسمة عل $2$ ، وأخذ الجذر التكعيبي لطرفي المعادلة ينتج	$$\begin{gathered} 2x=\frac{128}{x^2} \\ 2x^3=128 \\ \sqrt[3]{x^3}=\sqrt[3]{64} \\ x=4 \end{gathered}$$

  إذًا، لاقتران كمية المادة المستخدمة قيمة حرجة عند  $x=4$.

الخطوة 4: استخدم اختبار المشتقة الثانية لتصنيف القيمة الحرجة.

مشتقة اقتران كمية المادة	$A\text{'}\left(x\right)=\frac{-128}{x^2}+2x$
نشتق مشتقة اقتران كمية المادة	$A\text{'}\text{'}\left(x\right)=\frac{128\left(2x\right)}{{\left(x^2\right)}^2}+2$
بالتبسيط	$A\text{'}\text{'}\left(x\right)=\frac{256}{x^3}+2$
بتعويض $x=4$	$$\begin{gathered} A\text{'}\text{'}\left(4\right)=\frac{256}{{\left(4\right)}^3}+2 \\ =4+2=6>0 \end{gathered}$$

إذًا، بما أن $A\text{'}\text{'}\left(4\right)>0$ ، فإن لاقتران كمية المادة المستخدمة قيمة صغرى محلية عندما $x=4$ ، أي أن كمية المادة المستخدمة في صنع الصندوق أقل ما يمكن.

إذُا، طول قاعدة الصندوق $4 cm$ ، وعرضها $4 cm$ ، وارتفاع الصندوق  $2 cm$ ، لأن $h=\frac{32}{{\left(4\right)}^2}=\frac{32}{16}=2$

مثال 5: يريد مصنع إنتاج عُلب من الكرتون على شكل متوازي مستطيلات قاعدتها مربعة ومغلقة، بحيث يكون حجم العلبة الواحدة منها $64 c{m}^3$ ، أجد أبعاد العلبة الواحدة التي تجعل كمية المادة المستخدمة لصنعها أقل ما يمكن.

الحل: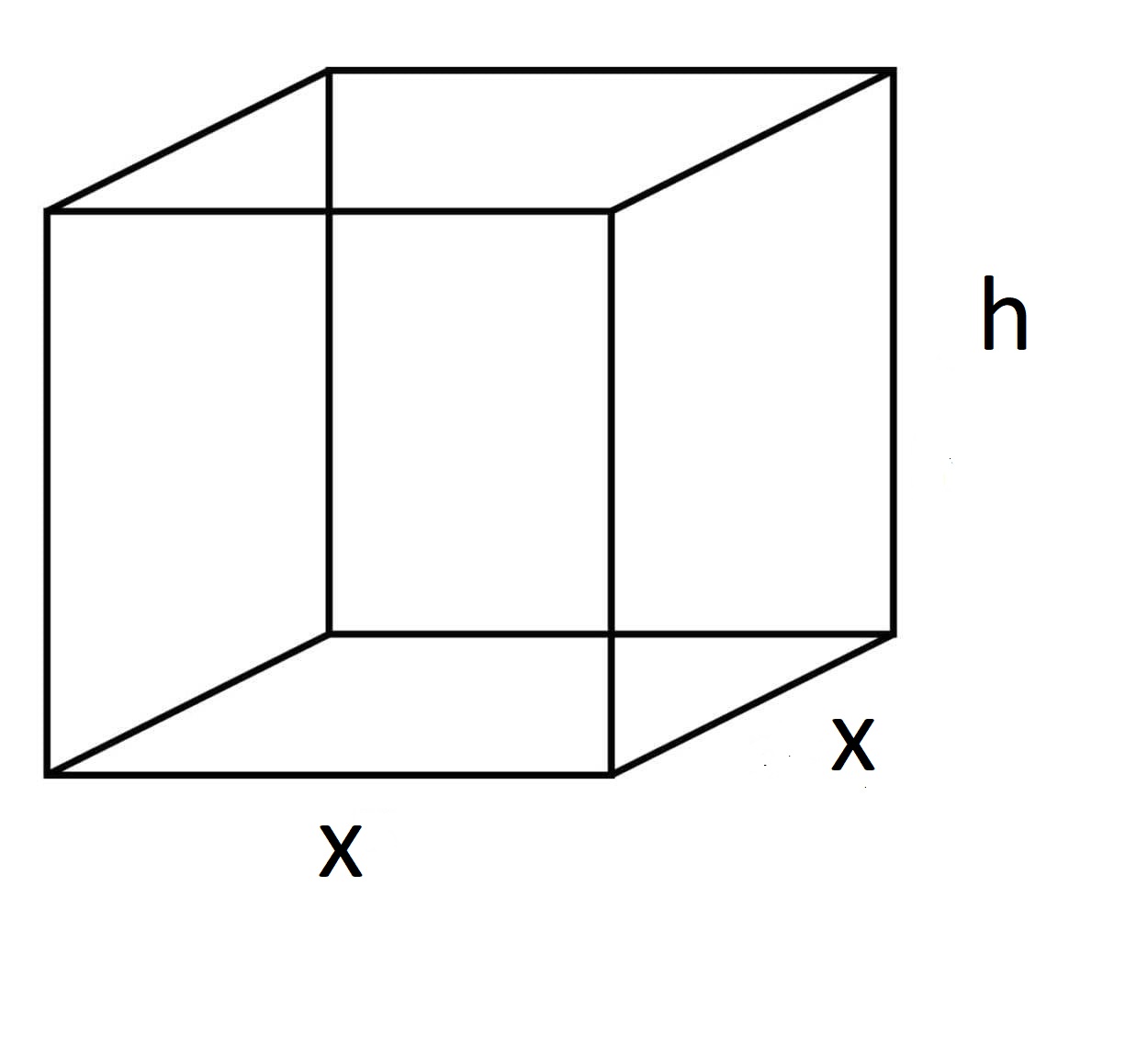

الخطوة 1: أرسم مخططًا وأضع عليه المتغيرات                                          

  افرض أن طول قاعدة العلبة $x$ ، وعرضها $x$ ، وارتفاعها $h$           كما هو موضح بالشكل

الخطوة 2: أكتب الاقتران الذي أريد إيجاد قيمته القصوى بدلالة متغير واحد.

• أجد اقتران كمية المادة المستخدمة كمية المادة المستخدمة في صنع الصندوق هي: المساحة الكلية لسطح العلبة.

  المساحة الكلية للعلبة  = المساحة الجانبية + مجموع مساحة القاعدتين                                                        المساحة الكلية للعلبة $S$ حيث       $S=4xh+2x^2$       

• أكتب $h$ بدلالة $x$ باستعمال حجم متوازي المستطيلات

حجم العلبة	$V=x^{2}h$
بتعويض $V=64$	$64=x^{2}h$
بكتابة  $h$ بدلالة $x$	$h=\frac{64}{x^2}$

•  أعوض $h=\frac{64}{x^2}$ في اقتران كمية المادة

اقتران كمية المادة	$S=4xh+2x^2$
نعوض $h=\frac{64}{x^2}$	$S\left(x\right)=4x\left(\frac{64}{x^2}\right)+2x^2$
بالتبسيط	$S\left(x\right)=\frac{256}{x}+2x^2$

   إذًا، الاقتران الذي يمثل كمية المادة المستخدمة هو: $S\left(x\right)=\frac{256}{x}+2x^2$

الخطوة 3: أجد القيم الحرجة للاقتران

اقتران الكمية المستخدمة	$S\left(x\right)=\frac{256}{x}+2x^2$
نشتق الاقتران	$S\text{'}\left(x\right)=\frac{-256}{x^2}+4x$
نساوي المشتقة بالصفر  $S\text{'}\left(x\right)=0$	$\frac{-256}{x^2}+4x=0$
بحل المعادلة من خلال إضافة $\frac{256}{x^2}$ لطرفي المعادلة والضرب التبادلي والقسمة على $4$  وأخذ الجذر التكعيبي  لطرفي المعادلة ينتج	$$\begin{gathered} 4x=\frac{256}{x^2} \\ 4x^3=256 \\ \sqrt[3]{x^3}=\sqrt[3]{64} \\ x=4 \end{gathered}$$

    إذًا، لاقتران الكمية المستخدمة قيمة حرجة عند $x=4$.     

الخطوة 4: أستخدم اختبار المشتقة الثانية لتصنيف القيمة الحرجة.    

مشتقة اقتران كمية المادة	$S\text{'}\left(x\right)=\frac{-256}{x^2}+4x$
نشتق مشتقة اقتران كمية المادة	$$\begin{gathered} S\text{'}\text{'}\left(x\right)=\frac{256\left(2x\right)}{{\left(x^2\right)}^2}+4 \\ =\frac{512}{x^3}+4 \end{gathered}$$
نعوض $x=4$	$$\begin{gathered} S\text{'}\text{'}\left(4\right)=\frac{512}{{\left(4\right)}^3}+4 \\ =8>0 \end{gathered}$$

إذًا، بما أن $S\text{'}\text{'}\left(4\right)>0$ فإن لاقتران كمية المادة قيمة صغرى محلية عن $x=4$ ، أي أن كمية المادة المستخدمة في صنع الصندوق أقل ما يمكن.

إذُا، طول قاعدة العلبة $4 cm$ ، وعرضها $4 cm$ ، وارتفاع العلبة $4 cm$ ،  لأن  $h=\frac{64}{{\left(4\right)}^2}=\frac{64}{16}=4$

أتحقق من فهمي

أراد حداد صناعة خزان ماء على شكل متوازي أضلاع مفلق ، قاعدته مربعة ، وحجمه $8 m^3$ ، جد أبعاد الخزان التي تجعل كمية المادة المستخدمة في صنعه أقل ما يمكن. 

الإجابة: أبعاد الخزان طول قاعدة الخزان $2 m$ ، وعرضها $2 m$ ، وارتفاع الخزان $2 m$

 

ج) إيجاد أكبر حجم ممكن

مثال 6: صفيحة من الكرتون المقوى مساحتها $42 c{m}^2$ ، أراد أحمد صناعة علبة مغلقة منها عل شكل متوازي مستطيلات قاعدته مربعة، جد أبعاد العلبة التي تجعل حجمها أكبر ما يمكن.

الحل: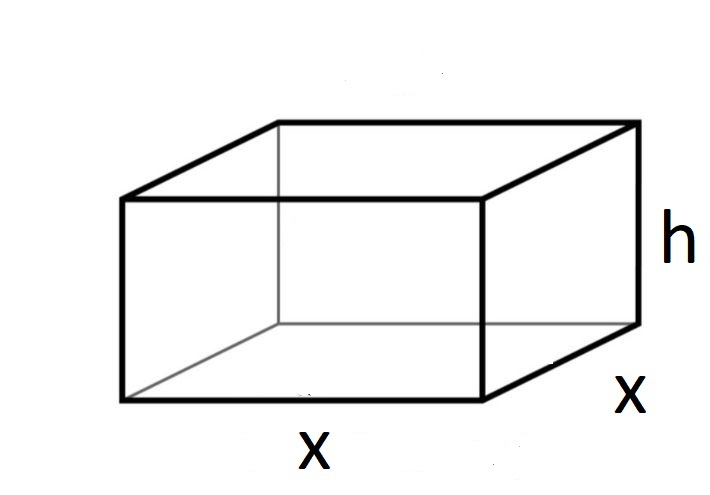

الخطوة 1: أرسم مخططًا وأضع عليه المتغيرات

افرض أن طول العلبة $x$ ، وعرضها $x$ ، وارتفاعها $h$

الخطوة 2: أكتب الاقتران الذي أريد إيجاد قيمته القصوى بدلالة متغير واحد.

• أجد اقتران الحجم   

                        حجم العلبة                                     $V=x^{2}h$

• أكتب $h$ بدلالة $x$ 

المساحة الكلية لسطح العلبة	$S=4xh+2x^2$
نساوي المساحة ب $42$ ونقسم المعادلة على $2$	$$\begin{gathered} 4xh+2x^2=42 \\ 2xh+x^2=21 \end{gathered}$$
نكتب $h$ بدلالة $x$	$$\begin{gathered} 2xh=21-x^2 \\ h=\frac{21-x^2}{2x} \end{gathered}$$

• أُعوض $h=\frac{21-x^2}{2x}$ في اقتران الحجم

اقتران الحجم	$V=x^{2}h$
بتعويض  $h=\frac{21-x^2}{2x}$	$V\left(x\right)=x^2\left(\frac{21-x^2}{2x}\right)$
بالتبسيط	$$\begin{gathered} V\left(x\right)=\frac{21x-x^3}{2} \\ =\frac{1}{2}\left(21x-x^3\right) \end{gathered}$$

إذًا، اقتران الحجم هو: $V\left(x\right)=\frac{1}{2}\left(21x-x^3\right)$

الخطوة 3: أجد القيم الحرجة للاقتران

اقتران الحجم	$V\left(x\right)=\frac{1}{2}\left(21x-x^3\right)$
نشتق الاقتران	$V\text{'}\left(x\right)=\frac{1}{2}\left(21-3x^2\right)$
نساوي المشتقة بالصفر  $V\text{'}\left(x\right)=0$	$\frac{1}{2}\left(21-3x^2\right)=0$
بضرب طرفي المعادلة في $2$	$21-3x^2$
بإضافة $-21$ لطرفي المعادلة والضرب في سالب	$$\begin{gathered} -3x^2=-21 \\ 3x^2=21 \end{gathered}$$
بقسمة المعادلة على $3$	$x^2=7$
بحل المعادلة	$x=\pm \sqrt{7}$

إذًا، بما أن الأبعاد موجبة فإن القيمة الحرجة للاقتران هي: $x=\sqrt{7}$

الخطوة 4: استخدم اختبار المشتقة الثانية لتصنيف القيمة الحرجة.

مشتقة اقتران الحجم	$V\text{'}\left(x\right)=\frac{1}{2}\left(21-3x^2\right)$
نشتق مشتقة اقتران الحجم	$$\begin{gathered} V\text{'}\text{'}\left(x\right)=\frac{1}{2}\left(-6x\right) \\ =-3x \end{gathered}$$
نعوض في المشتقة الثانية   $x=\sqrt{7}$	$$\begin{gathered} V\text{'}\text{'}\left(\sqrt{7}\right)=-3\left(\sqrt{7}\right) \\ =-3\sqrt{7}<0 \end{gathered}$$

إذًا، بما أن $V\text{'}\text{'}\left(\sqrt{7}\right)<0$، فإن لاقتران الحجم قيمة عظمى محلية عند $x=\sqrt{7}$ ، إي أن الحجم أكبر ما يمكن عندما $x=\sqrt{7}$.

إذُا، طول قاعدة العلبة $\sqrt{7} cm$ ، وعرضها $\sqrt{7} cm$ ، وارتفاعها $\sqrt{7} cm$ ، لأن       $h=\frac{21-{\left(\sqrt{7}\right)}^2}{2\left(\sqrt{7}\right)}=\frac{21-7}{2\sqrt{7}}=\frac{14}{2\sqrt{7}}=\frac{7}{\sqrt{7}}=\sqrt{7}$ 

 

مثال 7: يراد صنع صندوق مفتوح من أعلى من قطعة مربعة   الشكل طول ضلعها $12 cm$، وذلك بقص مربعات متساوية من أطرافها الأربعة ثم ثني الأجزاء البارزة للأعلى. جد أكبر حجم يمكن تكوينه بهذه الطريقة.

الحل: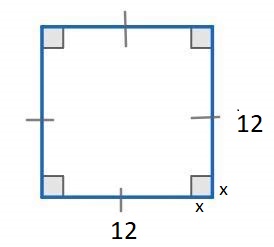

الخطوة 1: أرسم مخططًا ، وأضع عليه المتغيرات

أفرض أن طول ضلع المربع المراد قصه $x$

الخطوة 2: أكتب الاقتران الذي أريد إيجاد قيمته القصوى بدلالة متغير واحد.

• أجد اقتران الحجم   

حجم الصندوق =طول القاعدة $\times$ عرض القاعدة $\times$ الأرتفاع

طول القاعدة $\left(12-2x\right)$ ، عرض القاعدة $\left(12-2x\right)$ ، الأرتفاع $x$

اقتران الحجم	$V\left(x\right)=\left(12-2x\right)\left(12-2x\right)x$
بالتبسيط	$$\begin{gathered} V\left(x\right)=\left(144-48x+4x^2\right)\left(x\right) \\ =144x-48x^2+4x^3 \\ =4x^3-48x^2+144x \end{gathered}$$

   إذًا، اقتران الحجم هو: $V\left(x\right)=4x^3-48x^2+144x$.

الخطوة 3: أجد القيم الحرجة للاقتران

اقتران الحجم	$V\left(x\right)4x^3-48x^2+144x$
نشتق اقتران الحجم	$V\text{'}\left(x\right)=12x^2-96x+144$
نساوي المشتقة بالصفر $V\text{'}\left(x\right)=0$	$12x^2-96x+144=0$
بقسمة طرفي المعادلة على $12$	$x^2-8x+12=0$
بتحليل المعادلة	$\left(x-6\right)\left(x-2\right)=0$
ياستخدام خاصية الضرب الصفري	$x-6=0 or x-2=0$
بحل المعادلتين	$x=6 or x=2$

إذًا، لاقتران الحجم قيم حرجة عند  $x=6 , x=2$.

الخطوة 4: استخدم اختبار المشتقة الثانية لتصنيف القيمة الحرجة.

اقتران مشتقة الحجم	$V\text{'}\left(x\right)=12x^2-96x+144$
نشتق اقتران مشتقة الحجم	$V\text{'}\text{'}\left(x\right)=24x-96$
نعوض في المشتقة الثانية $x=6 , x=2$	$$\begin{gathered} V\text{'}\text{'}\left(6\right)=24\left(6\right)-96=48>0 \\ V\text{'}\text{'}\left(2\right)=24\left(2\right)-96=-48<0 \end{gathered}$$

إذًا، بما أن $V\text{'}\text{'}\left(x\right)>0$ فإن لاقتران الحجم قيمة صغرى محلية وبالتالي تهمل لأن المطلوب قيمة عظمى

وبما أن  $V\text{'}\text{'}\left(2\right)<0$ فإن لاقتران الحجم قيمة عظمى محلية عند $x=2$ ، إي أن حجم الصندوق أكبر ما يمكن عند$x=2$ ،

وأكبر حجم للصندوق هو $V\left(2\right)$ ويساوي   $128 c{m}^3$ لأن   $V\left(2\right)=4{\left(2\right)}^3-48{\left(2\right)}^2+144\left(2\right)=32-192+288=128$

 

أتحقق من فهمي 

صندوق على شكل متوازي مستطيلات، قاعدته مربعة الشكل، ومجموع أبعاده الثلاثة $120 cm$، أجد أبعاده التي تجعل حجمه أكبر ما يمكن.                                        الإجابة: طول قاعدة الصندوق $40 cm$، وعرضها $40 cm$، وأرتفاع الصندوق $40 cm$.

 

 

ثالثا: تطبيقات اقتصادية

هناك العديد من التطبيقات الاقتصادية المهمة على القيم القصوى ومنها: 

• إيجاد أقل تكلفة : يسمى الاقتران الذي يمثل تكلفة إنتاج $x$ وحدة من منتج معين اقتران التكلفة (cost function) ويرمز له بالرمز $C\left(x\right)$، ويسمى معدل تغير $C$ بالنسبة ل $x$ اقتران التكلفة الحدية (marginal cost) ويرمز له بالرمز $C\text{'}\left(x\right)$ .

                                   اقتران التكلفة الحدية هو مشتقة اقتران التكلفة

• إيجاد أكبر إيراد : يسمى الاقتران الذي يمثل إيراد بيع $x$ وحدة من منتج معين اقتران الإيراد (revenue function) ويرمز له بالرمز $R\left(x\right)$، ويسمى معدل تغير $R$ بالنسبة ل $x$ اقتران الإيراد الحدي (marginal revenue) ويرمز له بالرمز $R\text{'}\left(x\right)$

.                               اقتران الإيراد الحدي هو مشتقة اقتران الإيراد

• إيجاد أكبر ربح: يسمى الاقتران الذي يمثل ربح بيع $x$ وحدة من منتج معين اقتران الربح(profit function) ويرمز له بالرمز $P\left(x\right)$، ويسمى معدل تغير $P$ بالنسبة ل $x$ اقتران الربح الحدي(marginal profit) ويرمز له بالرمز $P\text{'}\left(x\right)$.

                                اقتران الربح الحدي هو مشتقة اقتران الربح

 

مثال 1: إذا كان اقتران التكلفة لإنتاج $x$ قطعة من منتج ما مُعطى بالاقتران: $C\left(x\right)=x^2-3x+200$دينار، جد التكلفة الحدية لإنتاج $\left(8\right)$ قطع.

الحل:

الخطوة 1: أجد مشتقة اقتران التكلفة

اقتران التكلفة	$C\left(x\right)=x^2-3x+200$
نشتق الاقتران	$C\text{'}\left(x\right)=2x-3$

إذًا، اقتران التكلفة الحدية هو: $C\text{'}\left(x\right)=2x-3$

الخطوة 2: أجد التكلفة الحدية عندما $x=8$

اقتران التكلفة الحدية	$C\text{'}\left(x\right)=2x-3$
نعوض $x=8$	$C\text{'}\left(8\right)=2\left(8\right)-3$
بالتبسيط	$$\begin{gathered} C\text{'}\left(8\right)=16-3 \\ =13 \end{gathered}$$

إذًا، التكلفة الحدية لإنتاج $8$ قطع هي: $13$دينار.

 

مثال 2: إذا كان اقتران الإيراد للمبيعات في إحدى المولات هو $R\left(x\right)=2x^3+30x$ دينار، حيث $x$ عدد الوحدات المنتجة من سلعة ما، أجد الإيراد الحدي الناتج عن بيع $\left(10\right)$ وحدات.

الحل:

الخطوة 1: أجد مشتقة اقتران الإيراد

اقتران الإيراد	$R\left(x\right)=2x^3+30x$
نشتق اقتران	$R\text{'}\left(x\right)=6x^2+30$

الخطوة 2: أجد الإيراد الحدي عندما  $x=10$ 

اقتران الإيراد الحدي	$R\text{'}\left(x\right)=6x^2+30$
نعوض $x=10$	$R\text{'}\left(10\right)=6{\left(10\right)}^2+30$
بالتبسيط	$$\begin{gathered} R\text{'}\left(10\right)=6\left(100\right)+30 \\ =600+30 \\ =630 \end{gathered}$$

إذًا، الإيراد الحدي لبيع $\left(10\right)$ وحدات هو: $630$ دينار.

 

مثال 3: يبيع محل $x$ قطعة اسبوعيًا من منتج معين، فإذا كان اقتران الربح هو $P\left(x\right)=2x^2+280x-200$، أجد الربح الحدي لبيع $\left(100\right)$ قطعة,

الخطوة 1: أجد مشتقة اقتران الربح

اقتران الربح	$P\left(x\right)=2x^2+280x-200$
نشتق الاقتران	$P\text{'}\left(x\right)=4x+280$

إذًا، اقتران الربح الحدي هو: $P\text{'}\left(x\right)=4x+280$

الخطوة الثانية: أجد الربح الحدي عندما $x=100$

اقتران الربح الحدي	$P\left(x\right)=4x+280$
نعوض   $x=100$	$P\left(100\right)=4\left(100\right)+280$
بالتبسيط	$$\begin{gathered} P\left(100\right)=400=280 \\ =680 \end{gathered}$$

إذًا، الربح الحدي لبيع $\left(100\right)$ قطعة أسبوعيًا هو: $680$ دينار.

 

مثال 4: إذا كان الإبراد الناتج عن بيع $x$ قطعة من منتج ما هو: $R\left(x\right)=50x-x^2$، والتكلفة هي: $C\left(x\right)=20x$، أجد قيمة $x$ ، أجد قيمة $x$ التي تجعل الربح أكبر ما يمكن.

الحل: 

الخطوة 1: أجد اقتران الربح

                                 الربح = الإيراد - التكلفة

اقتران الربح = اقتران الإيراد - اقتران التكلفة

                                   $P\left(x\right)=R\left(x\right)-C\left(x\right)$

اقتران الربح

$$\begin{gathered} P\left(x\right)=R\left(x\right)-C\left(x\right) \\ =\left(50x-x^2\right)-\left(20x\right) \\ =50x-x^2-20x \\ =30x-x^2 \end{gathered}$$

إذًا، اقتران الربح هو:  $P\left(x\right)=30x-x^2$

الخطوة 2: أجد القيمة الحرجة لاقتران الربح

اقتران الربح	$P\left(x\right)=30x-x^2$
الربح الحدي	$P\text{'}\left(x\right)=30-2x$
نساوي الربح الحدي بالصفر$P\left(x\right)=0$	$30-2x=0$
بحل المعادلة من خلال إضافة $-30$ لطرفي المعادلة القسمة على$-2$	$$\begin{gathered} -2x=-30 \\ x=\frac{-30}{-2} \\ x=15 \end{gathered}$$

إذًا، القيمة الحرجة لاقتران الربح هي:$x=15$

الخطوة 3:أستعمل اختبار المشتقة الثانية لتحديد نوع القيمة الحرجة

اقتران الربح الحدي	$P\text{'}\left(x\right)=30-2x$
نشتق اقتران الربح الحدي	$P\text{'}\text{'}\left(x\right)=-2<0$

إذًا، بما أن $P\text{'}\text{'}\left(x\right)<0$ لجميع قيم $x$ الموجبة ، فإن لاقتران الربح قيمة عظمى محلية عندما $x=15$ ؛ أي أن قيمة $x$ التي تجعل  الربح أكبر ما يمكن هي:$15$قطعة

 

مثال 5: ينتج مصنع للحواسيب $x$ جهاز أسبوعيًا، فإذا كانت تكلفة الإنتاج الأسبوعي تُعطى وفق الاقتران: $C\left(x\right)=x^2+100x+2000$، وكان المصنع يبيع الجهاز الواحد بمبلغ $\left(300\right)$ دينار ، فأجد عدد الأجهزة التي يجب إنتاجها وبيعها لتحقيق أكبر ربح ممكن.

الحل: 

الخطوة 1: أجد اقتران الإيراد

اقتران الإيراد ويساوي السعر $\times$ الكمية

$R\left(x\right)=300x$

إذًا، اقتران الإيراد هو:   $R\left(x\right)=300x$

الخطوة 2: أجد اقتران الربح

اقتران الربح = اقتران الإيراد - اقتران التكلفة	$P\left(x\right)=R\left(x\right)-C\left(x\right)$
نعوض $$\begin{gathered} R\left(x\right)=300x \\ C\left(x\right)=x^2+100x+2000 \end{gathered}$$	$P\left(x\right)=300x-\left(x^2+100x+2000\right)$
بالتبسيط	$$\begin{gathered} P\left(x\right)=300x-x^2-100x-2000 \\ =-x^2+200x-2000 \end{gathered}$$

إذًا، اقتران الربح هو: $P\left(x\right)=-x^2+200x-2000$

الخطوة 3: أجد القيمة الحرجة لاقتران الربح

اقتران الربح	$P\left(x\right)=-x^2+200x-2000$
اقتران الربح الحدي	$P\text{'}\left(x\right)=-2x+200$
نساوي الربح الحدي بالصفر $P\text{'}\left(x\right)=0$	$-2x+200=0$
بحل المعادلة من خلال إضافة $-200$ لطرفي المعادلة والقسمة على $-2$	$$\begin{gathered} -2X=-200 \\ X=\frac{-200}{-2} \\ X=100 \end{gathered}$$

إذًا، القيمة الحرجة لاقتران الربح هي: $x=100$

الخطوة 4:أستعمل اختبار المشتقة الثانية لتحديد نوع القيمة الحرجة

اقتران الربح الحدي	$P\text{'}\left(x\right)=-2x+200$
نشتق اقتران الربح الحدي	$P\text{'}\text{'}\left(x\right)=-2<0$

إذًا، بما أن $P\text{'}\text{'}\left(x\right)<0$ لجميع قيم $x$ الموجبة، فإن لاقتران الربح قيمة عظمى محلية عندما $x=100$ ؛ أي أن عدد الأجهزة التي يجب إنتاجها وبيعها لتحقيق أكبر ربح هو: $\left(100\right)$جهاز.

 

مثال 6: ينتج مصنع ثلاجات $x$ ثلاجة أسبوعيًا، فإذا كانت تكلفة الإنتاج الأسبوعي بالدينار تعطى وفق الاقتران: $C\left(x\right)=x^2+50x+4200$، وكان سعر الثلاجة $\left(550\right)$ دينار، فما عدد الثلاجات التي يجب إنتاجها وبيعها أسبوعيًا لتحقيق أكبر ربح ممكن.

الحل:

الخطوة 1: أجد اقتران الإيراد

اقتران الإيراد = السعر $\times$ الكمية

$R\left(x\right)=550x$

الخطوة 2: أجد اقتران الربح 

اقتران الربح=اقتران الإيراد - اقتران التكلفة	$$\begin{gathered} P\left(x\right)=R\left(x\right)-C\left(x\right) \\ P\left(x\right)=550x-\left(x^2+50x+4200\right) \end{gathered}$$
بالتبسيط	$$\begin{gathered} P\left(x\right)=550x-x^2-50x-4200 \\ =500x-x^2-4200 \\ =-x^2+500x-4200 \end{gathered}$$

إذًا، اقتران الربح هو: $P\left(x\right)=-x^2+500x-4200$

الخطوة 3: أجد القيمة الحرجة لاقتران الربح

اقتران الربح	$P\left(x\right)=-x^2+500x-4200$
اقتران الربح الحدي	$P\text{'}\left(x\right)=-2x+500$
نساوي اقتران الربح الحدي بالصفر $P\text{'}\left(x\right)=0$	$-2x+500=0$
بحل المعادلة من خلال إضافة $-500$ والقسمة على $-2$	$$\begin{gathered} -2x=-500 \\ x=\frac{-500}{-2}=\frac{500}{2} \\ =250 \end{gathered}$$

إذًا،  القيمة الحرجة لاقتران الربح هي: $x=250$

 الخطوة 4: أستعمل اختبار المشتقة الثانية لتحديد نوع القيمة الحرجة

اقتران الربح الحدي	$P\text{'}\left(x\right)=-2x+500$
نشتق اقتران الربح الحدي	$P\text{'}\text{'}\left(x\right)=-2<0$

إذًا، بما أن $P\text{'}\text{'}\left(x\right)<0$ لجميع قيم $x$ الموجبة ، فإن لاقتران الربح قيمة عظمى محلية عندما $x=250$ ؛ أي أن عدد  الثلاجات التي يجب إنتاجها وبيعها أسبوعيًا لتحقيق أكبر ربح هو: $\left(250\right)$ ثلاجة.

 

أتحقق من فهمي

1. إذا كانت تكلفة إنتاج $x$ وحدة من منتج معين تعُطى وفق الاقتران: $C\left(x\right)=3x^2+70x+1500$ دينار، جد التكلفة الحدية لإنتاج $\left(10\right)$ وحدات من هذا المنتج.                                                                الإجابة: التكلفة الحدية هي: $\left(130\right)$ دينار.

2. إذا كان الإيراد الناتج عن بيع $x$ لعبة من إنتاج مصنع ألعاب يعُطى وفق الاقتران:$R\left(x\right)=0.2x^3+40x$، جد الإيراد الحدي لبيع $\left(20\right)$ لعبة.                                                                                           الإجابة: الإيراد الحدي هو: $\left(280\right)$ دينار.

3. يبيع مصنع غرفة النوم الواحدة بمبلغ $\left(2500\right)$دينار ، فإذا كانت تكلفة إنتاج $x$ غرفة شهرًا تعُطى وفق الاقتران:  $C\left(x\right)=5x^2+2000x+7500$ دينار، جد عدد غرف النوم التي يجب إنتاجها وبيعها لتحقيق أكبر ربح ممكن.                                                                                                                                                                                          الإجابة: عدد غرف النوم هو:$\left(50\right)$ غرفة