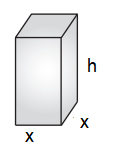الرياضيات فصل أول

تطبيقات القيم القصوى

أتحقق من فهمي ( صفحة 108)

إذا كان: $f\left(x\right)=x^{3 }- 2x^{2 }-4x + 5$، فاستعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية للاقتران.

الحل: 

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران.

الاقتران المعطى	$f\left(x\right)=x^3 - 2x^2 - 4x + 5$
المشتقة الأولى	$f \text{'}\left(x\right)=3x^2 - 4x - 4$
نساوي المشتقة بالصفر  $f \text{'}\left(x\right)=0$	$3x^2 -4x - 4=0$
بتحليل المعادلة	$\left(3x + 2\right)\left(x - 2\right)=0$
باستعمال خاصية الضرب الصفري	$3x + 2=0 or x-2=0$
بحل المعادلتين	$$\begin{gathered} 3x=-2 or x=2 \\ x=\frac{-2}{3} \end{gathered}$$

إذًا، القيم الحرجة للاقتران $f$ هي: $x=\frac{-2}{3} , x=2$.

الخطوة 2: أجد المشتقة الثانية.

اقتران المشتقة الأولى	$f \text{'}\left(x\right)=3x^2 - 4x - 4$
اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=6x - 4$

الخطوة 3: أُعوض القيم الحرجة في المشتقة الثانية؛ لتحديد نوعها.

المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=6x - 4$
بتعويض  $x=\frac{-2}{3} , x=2$	$$\begin{gathered} f\text{'}\text{'}\left(2\right)=6\left(2\right) - 4 \\ =12 - 4 \\ =8 >0 \\ f\text{'}\text{'}\left(\frac{-2}{3}\right)=6 \left(\frac{-2}{3}\right) - 4 \\ =-4 - 4 \\ =-8 <0 \end{gathered}$$

إذًا، بما أن $f\text{'}\text{'}\left(2\right)=8>0$، فإن للاقتران $f$ قيمة صغرى محلية عند $x=2$، وهي: $f\left(2\right)=-3$، لأن   $f\left(2\right)={\left(2\right)}^3 -2{\left(2\right)}^2 - 4\left(2\right) + 5=-3$.

بما أن $f\text{'}\text{'}\left(\frac{-2}{3}\right) =-8<0$، فإن للاقتران $f$ قيمة عظمى محلية عند $x=\frac{-2}{3}$، وهي: $f \left(\frac{-2}{3}\right)=\frac{175}{27}$، لأن        $$\begin{gathered} f \left(\frac{-2}{3}\right)={\left(\frac{-2}{3}\right)}^3 - 2 {\left(\frac{-2}{3}\right)}^2 - 4 \left(\frac{-2}{3}\right) + 5 =\frac{-8}{27} - 2 \left(\frac{4}{9}\right) +\frac{8 }{3}+ 5 \\ =\frac{-8}{27} - \frac{8}{9} + \frac{8}{3}+ 5=\frac{-8}{27} - \frac{24}{27} +\frac{72}{27} +\frac{135}{27}=\frac{175}{27} \end{gathered}$$    

أتحقق من فهمي (صفحة 110) 

بنى نجار سقفًا خشبيًا لحظيرة حيوانات، وكان السقف على شكل مستطيل محيطه $54 m$. أجد أكبر مساحة ممكنة لسطح الحظيرة.

الحل: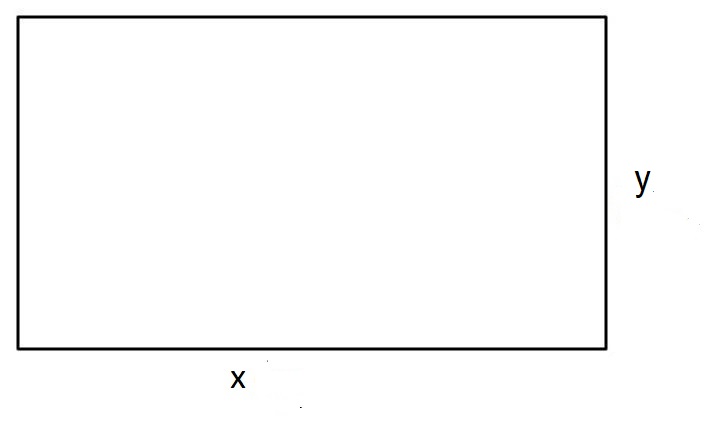 

الخطوة 1: أرسم مخططًا.

افترض أن $x$ هو طول السقف، $y$ هو عرضه كما في المخطط المجاور

الخطوة 2: أكتب الاقتران الذي أُريد إيجاد قيمته القصوى بدلالة متغير واحد.

• أجد مساحة اقتران السقف

                     مساحة المستطيل = الطول $\times$ العرض    $\Leftarrow$      $A=x y$

• أكتب $y$ بدلالة $x$ باستعمال المحيط. 

محيط السقف	$p=2x + 2y$
بتعويض $p=54$	$2x + 2y=54$
بقسمة طرفي المعادلة على $2$	$x + y=27$
بكتابة $y$ بدلالة $x$	$y=27 - x$

• أُعوض $y$ في اقتران مساحة السقف.

اقتران مساحة السقف	$A=x y$
بتعويض  $y=27 - x$	$A\left(x\right)=x \left(27 - x\right)$
بالتبسيط	$A\left(x\right)=27x - x^2$

إذًا، الاقتران الذي يمثل مساحة السقف هو:  $A\left(X\right)=27x - x^2$.

الخطوة 3: أجد القيم الحرجة للاقتران.

اقتران مساحة السقف	$A\left(x\right)=27x - x^2$
بإشتقاق اقتران المساحة	$A\text{'}\left(x\right)=27 - 2x$
بمساواة مشتقة اقتران المساحة بالصفر $A\text{'}\left(x\right)=0$	$27 - 2x=0$
بحل المعادلة	$$\begin{gathered} -2x=-27 \\ x=\frac{-27}{-2} \\ =\frac{27}{2} \end{gathered}$$

إذًا، القيمة الحرجة للاقتران $f$ هي:  $x=\frac{27}{2}$

الخطوة 4: استعمل اختبار المشتقة الثانية  لتحديد نوع القيمة الحرجة $x=\frac{27}{2}$.

مشتقة اقتران المساحة	$A\text{'}\left(x\right)=27 - 2x$
المشتقة الثانية لاقتران المساحة	$A\text{'}\text{'}\left(x\right)=-2$

إذًا، بما أن $A\text{'}\text{'}\left(x\right)=-2 <0$ لجميع قيم $x$ الموجبة، فإن لاقتران المساحة قيمة عظمى محلية عند $x=\frac{27}{2}$، أي أن مساحة السقف أكبر ما يمكن إذا كان طول السقف $x=\frac{27}{2} m$ ، وعرضه $y=27 -\frac{27}{2}=\frac{27}{2} m$.

أتحقق من فهمي ( صفحة 111)

أرادت إحدى الشركات أن تصنع  خزانات معدنية على شكل متوازي مستطيلات مغلق، بحيث يكون حجم كل منها $2 m^3$، وقاعدته مربعة الشكل. أجد أبعاد الخزان الواحد التي تجعل كمية المعدن المستعملة لصنعه أقل ما يمكن.

الحل: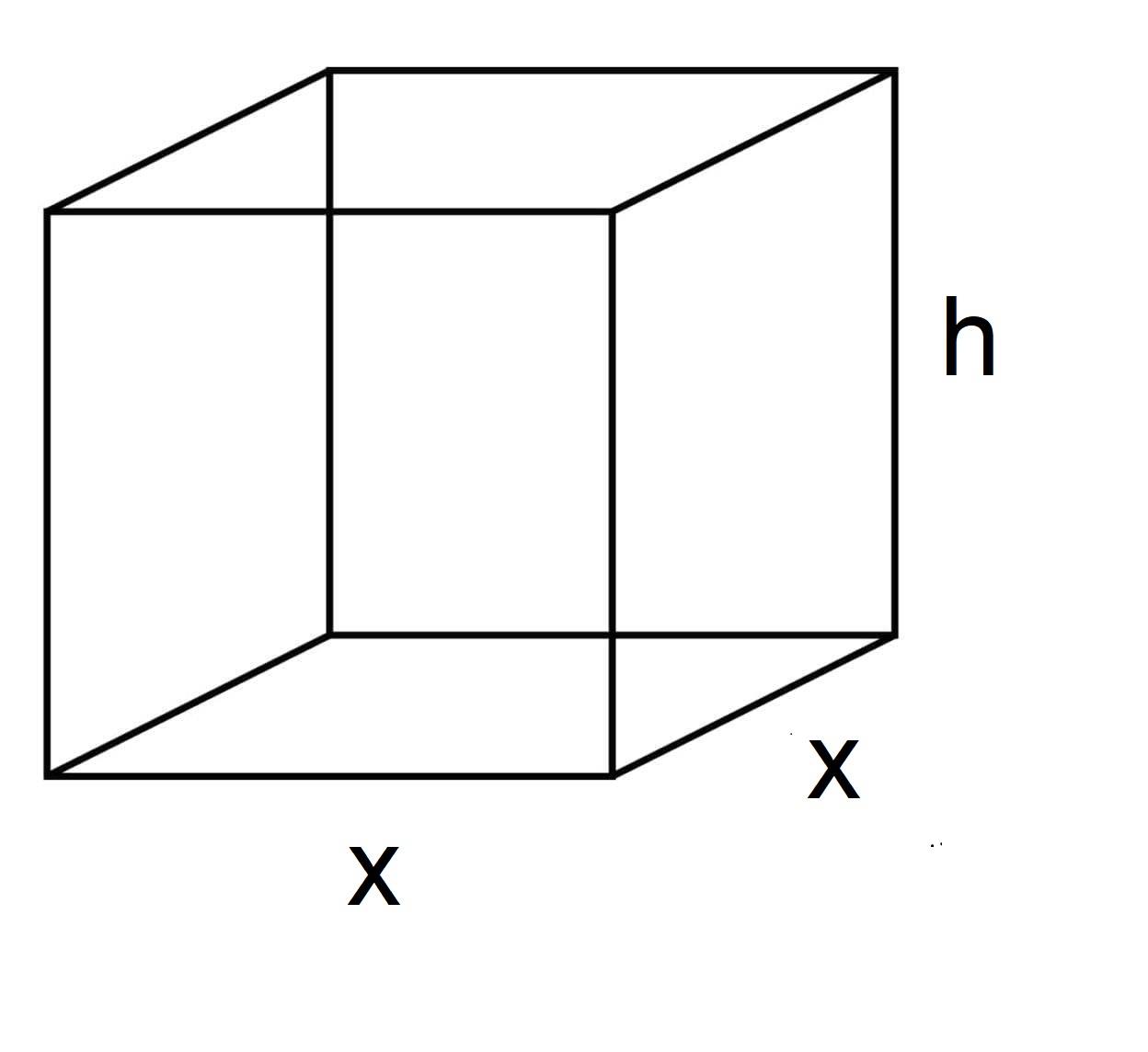

الخطوة 1: أرسم مخططًا.

افترض أن طول قاعدة الخزان $x$ ، وارتفاع الخزان $h$ كما في المخطط المجاور.

الخطوة 2:  أكتب الاقتران الذي أُريد إيجاد قيمته القصوى  بدلالة متغير واحد.

• أجد اقتران كمية المادة المستعملة في صنعه.

كمية المادة المستعملة في صنعه هي المساحة الكلية للخزان.

اقتران المساحة الكلية للخزان   $S=4x h + 2x^2 \Leftarrow$

• أكتب $h$ بدلالة $x$ باستعمال حجم الخزان.

حجم الخزان	$V=x^2 h$
بتعويض  $V=2$	$2=x^2 h$
بكتابة $h$ بدلالة $x$	$h=\frac{2}{x^2}$

• أُعوض $h$ في اقتران المساحة الكلية للخزان.

اقتران المساحة الكلية	$S= 4x h + 2x^2$
بتعويض  $h=\frac{2}{x^2}$	$S=4x \left(\frac{2}{x^2}\right) + 2x^2$
بالتبسيط	$S=\frac{8}{x} + 2x^2$

إذًا، اقتران المساحة الكلية لسطح الخزان هو: $S=\frac{8}{x} + 2x^2$.

الخطوة 3: أجد القيم الحرجة للاقتران.

اقتران المساحة الكلية للخزان	$S=\frac{8}{x} + 2x^2$
باشتقاق اقتران المساحة الكلية	$S\text{'}\left(x\right)=\frac{-8}{x^2} + 4x$
بمساواة المشتقة بالصفر  $S\text{'}\left(x\right)=0$	$\frac{-8}{x^2} +4x=0$
بحل المعادلة من خلال إضافة$-4x$ لطرفي المعادلة الضرب التبادلي بقسمة طرفي المعادلة على $-4$ بأخذ الجذر التكعيبي لطرفي المعادلة	$$\begin{gathered} \frac{-8}{x^2}=-4x \\ -4x^3=-8 \\ {x}^3=2 \\ \sqrt[3]{x^3}=\sqrt[3]{2} \\ x=\sqrt[3]{2} \end{gathered}$$

إذًا، للاقتران قيمة حرجة واحدة وهي: $x=\sqrt[3]{2}$.

الخطوة 4: استعمل اختبار المشتقة الثانية لتحديد نوع القيمة الحرجة: $x=\sqrt[3]{2}$.

مشتقة اقتران المساحة الكلية	$S\text{'}\left(x\right)=\frac{-8}{x^2} + 4x$
المشتقة الثانية لاقتران المساحة الكلية بالتبسيط	$$\begin{gathered} S\text{'}\text{'}\left(x\right)=\frac{\left(-8\right)\left(-2x\right)}{{\left(x^2\right)}^2} + 4 \\ =\frac{16}{x^3} + 4 \end{gathered}$$
بتعويض $x=\sqrt[3]{2}$	$$\begin{gathered} S\text{'}\text{'}\left(\sqrt[3]{2}\right)=\frac{16}{{\left(\sqrt[3]{2} \right)}^3} + 4 \\ =\frac{16}{2} + 4=8 + 4 \\ =12 \end{gathered}$$

إذًا، بما أن $S\text{'}\text{'}\left(\sqrt[3]{2} \right)=12 >0$ فإن للاقتران قيمة صغرى محلية عند $x=\sqrt[3]{2}$ ؛ أي أن المساحة الكلية للخزان  أقل ما يمكن عندما يكون طول ضلع قاعدة الخزان  $x=\sqrt[3]{2} m$ وارتفاعه $h=\frac{2}{{\left(\sqrt[3]{2} \right)}^2}=\frac{2}{\sqrt[3]{4}} m$.

أتحقق من فهمي ( صفحة 113)

لدى حداد صفيحة  معدنية  مساحتها $54 m^2$. أراد الحداد أن يصنع منها خزان ماء على شكل متوازي مستطيلات مغلق، وأن يكون الخزان مفتوحًا من الأعلى ، وقاعدته مربعة الشكل. أجد أبعاد الخزان التي تجعل حجمه أكبر ما يمكن.

الحل:

الخطوة الأولى 1: أرسم مخططًا.

افترض أن طول قاعدة الخزان $x$، وارتفاع الخزان $h$ كما في المخطط المجاور.

 

الخطوة 2:  أكتب الاقتران الذي أُريد إيجاد قيمته القصوى  بدلالة متغير واحد.

• أجد اقتران حجم الخزان.

حجم الخزان	$V=l \times w \times h$
بتعويض $l=x , w=x$	$V=x \times x \times h$
بالتبسيط	$V=x^2 h$

• أكتب $h$ بدلالة $x$ باستعمال مساحة سطح الخزان.

مساحة سطح الخزان ( المساحة الجانبية + مساحة القاعدة)	$S=4x h + x^2$
بتعويض  $S=54$	$54=4x h + x^2$
بكتابة $h$ بدلالة $x$	$$\begin{gathered} 4x h=54-x^2 \\ h=\frac{54 - x^2}{4x} \end{gathered}$$

• أُعوض $h$ في اقتران حجم الخزان.

اقتران حجم الخزان	$V=x^2 h$
بتعويض $h=\frac{54 -x^2}{4x}$	$V\left(x\right)=x^2\left(\frac{54 - x^2}{4x}\right)$
بالتبسيط	$$\begin{gathered} V\left(x\right)=\frac{54x - x^3}{4} \\ V\left(x\right)=\frac{1}{4}\left(54x - x^3\right) \end{gathered}$$

الخطوة 3: أجد القيم الحرجة للاقتران.

اقتران حجم الخزان	$V\left(x\right)=\frac{1}{4}\left(54x - x^3\right)$
بإشتقاق اقتران الحجم	$V\text{'}\left(x\right)=\frac{1}{4}\left(54 - 3x^2\right)$
بمساواة المشتقة بالصفر  $V\text{'}\left(x\right)=0$	$\frac{1}{4}\left(54 - 3x^2\right)=0$
بضرب طرفي المعادلة ب $4$	$54 - 3x^2=0$
بقسمة طرفي المعادلة عل $3$	$18 -x^2=0$
بإضافة $-18$ لطرفي المعادلة	$$\begin{gathered} - x^2=-18 \\ {x}^2=18 \end{gathered}$$
بأخذ الجذر التربيعي لطرفي المعادلة	$$\begin{gathered} \sqrt{x^2}=\pm \sqrt{18} \mathrm{موجب} \mathrm{عدد} x \mathrm{لكن} \\ =\sqrt{2\times 9}=3\sqrt{2} \\ x=3\sqrt{2} \end{gathered}$$

إذًا، للاقتران قيمة حرجة واحدة وهي: $x=3\sqrt{2}$.

الخطوة 4: استعمل اختبار المشتقة الثانية لتحديد نوع القيمة الحرجة: $x=3\sqrt{2}$.

اقتران المشتقة الأولى للحجم	$V\text{'}\left(x\right)=\frac{1}{4}\left(54 - 3x^2\right)$
اقتران المشتقة الثانية للحجم	$$\begin{gathered} V\text{'}\text{'}\left(X\right)=\frac{1}{4}\left(- 6x\right) \\ =\frac{-3}{2}x \end{gathered}$$
,بتعويض $x=3\sqrt{2}$	$$\begin{gathered} V\text{'}\text{'}\left(3\sqrt{2} \right)=\frac{-3}{2}\left(3\sqrt{2} \right) \\ =\frac{-9\sqrt{2}}{2} \end{gathered}$$

إذًا، بما أن  $V\text{'}\text{'}\left(3\sqrt{2}\right)<0$، فإن لاقتران الحجم قيمة عظمى محلية عند $x=3\sqrt{2}$؛ أي أن حجم الخزان يكون أكبر ما يمكن عندما يكون طول ضلع قاعدة الخزان $x=3\sqrt{2} m$ وارتفاعه        $h=\frac{3\sqrt{2}}{2} m$    لأن       $h=\frac{54 -{\left( 3\sqrt{2}\right)}^{2^{}}}{4\left(3\sqrt{2}\right)}=\frac{54 -18}{12\sqrt{2}} =\frac{36}{12\sqrt{2}}=\frac{3}{\sqrt{2}}=\frac{3\sqrt{2}}{2}$

أتحقق من فهمي ( صفحة 115)

وجدت خبيرة تسويق أنه لبيع $x$ ثلاجة من نوع جديد، فإن سعرالثلاجة الواحدة ( بالدينار) يجب أن يكون: $s\left(x\right)=1750 - 2x$، حيث $x$ عدد الأجهزة المبيعة. إذا كانت تكلفة إنتاج $x$ من هذه الأجهزة تعطى بالاقتران: $C\left(x\right)=2250 + 18x$، فأجد عدد الأجهزة التي يجب إنتاجها وبيعها لتحقيق أكبر ربح ممكن.

الحل:

الخطوة 1: أجد اقتران الإيراد.

اقتران الإيراد =الكمية $\times$ السعر            $$\begin{gathered} R\left(x\right)=x \left(1750 - 2x\right) \Leftarrow \\ R\left(x\right)=1750x - 2x^2 \end{gathered}$$

الخطوة 2: أجد اقتران الربح.

اقتران الربح = اقتران الإيراد - اقتران التكلفة

اقتران الربح	$P\left(x\right)=R\left(x\right)-C\left(x\right)$
بتعويض $$\begin{gathered} R\left(x\right)=1750x -2x^2 \\ C\left(x\right)=2250 + 18x \end{gathered}$$	$P\left(x\right)=\left(1750x - 2x^2\right)-\left(2250 + 18x\right)$
بالتبسيط	$$\begin{gathered} P\left(x\right)=1750x - 2x^2 - 2250 - 18x \\ =- 2x^2 +1732x - 2250 \end{gathered}$$

إذًا، اقتران الربح هو: $P\left(x\right)=-2x^2 +1732x - 2250$.

الخطوة 3: أجد القيم الحرجة لاقتران الربح.

اقتران الربح	$P\left(x\right)=-2x^2 + 1732x - 2250$
اقتران الربح الحدي	$P\text{'}\left(x\right)=-4x +1732$
بمساواة اقتران الربح الحدي بالصفر   $P\text{'}\left(x\right)=0$	$-4x + 1732=0$
بحل المعادلة: إضافة $-1732$ لطرفي المعادلة	$-4x=-1732$
بضرب طرفي المعادلة ب $-1$	$4x=1732$
بقسمة طرفي المعادلة على$4$	$$\begin{gathered} x=\frac{1732}{4} \\ x=433 \end{gathered}$$

الخطوة 4: استعمل اختبار المشتقة الثانية لتحديد نوع القيمة الحرجة: $x=433$.

اقتران الربح الحدي	$P\text{'}\left(X\right)=-4X + 1732$
اقتران المشتقة الثانية للربح	$P\text{'}\text{'}\left(x\right)=-4$

إذًا، بما أن $P\text{'}\text{'}\left(x\right)<0$ لجميع قيم $x$ الموجبة، فإن لاقتران الربح قيمة عظمى محلية عند $x=433$.؛ أي أن الربح أكبر ما يمكن عند إنتاج وبيع $433$ ثلاجة.

أتدرَّب وأحُلُّ المسائل ( صفحة 116)

1) أستعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية (إن وجدت) للاقتران: $f\left(x\right)=x^2 - 2x + 5$.

الحل:

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران.

الاقتران المعطى	$f\left(x\right)=x^2 - 2x + 5$
أشتق الاقتران	$f \text{'}\left(x\right)=2x - 2$
بمساواة المشتقة بالصفر  $f \text{'}\left(x\right)=0$	$2x - 2=0$
بحل المعادلة: إضافة $2$ لطرفي المعادلة	$2x=2$
بقسمة طرفي المعادلة على $2$	$x=1$

إذًا، القيمة الحرجة للاقتران $f$ هي: $x=1$.

الخطوة 2: أجد المشتقة الثانية للاقتران.

اقتران المشتقة الأولى	$f \text{'}\left(x\right)=2x - 2$
المشتقة الثانية للاقتران	$f\text{'}\text{'}\left(x\right)=2$

الخطوة 3: أُعوض القيمة الحرجة في المشتقة الثانية؛ لتحديد نوعها.

اقتران المشتقة الثانية

$f\text{'}\text{'}\left(x\right)=2$

إذًا، بما أن  $f\text{'}\text{'}\left(x\right)>0$ لجميع قيم $x$ الحقيقية، فإن للاقتران قيمة صغرى محلية عندة$x=1$، وهي: $f\left(1\right)=4$ ، لأن$f\left(1\right)={\left(1\right)}^2 - 2\left(1\right) + 5$.

2) أستعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية (إن وجدت) للاقتران: $f\left(x\right)=20 + 15x - x^2 -\frac{x^3}{3}$.

الحل:

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران.

الاقتران المعطى	$f\left(x\right)=20 + 15x - x^2 - \frac{x^3}{3}$
أشتق الاقتران	$f \text{'}\left(x\right)=15 -2x - x^2$
بمساواة المشتقة بالصفر  $f \text{'}\left(x\right)=0$	$15 - 2x - x^2=0$
بتحليل المعادلة	$\left(5 + x\right)\left(3 - x\right)=0$
باستعمال خاصية الضرب الصفري	$5 + x=0 or 3 - x=0$
بحل المعادلتين	$x=-5 or x=3$

إذًا، القيمl الحرجة للاقتران $f$ هي: $x=-5 , x=3$.

الخطوة 2: أجد المشتقة الثانية للاقتران.

اقتران المشتقة الأولى	$f \text{'}\left(x\right)=15 -2x - x^2$
اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=-2 - 2x$

الخطوة 3: أُعوض القيم الحرجة في المشتقة الثانية؛ لتحديد نوعها.

اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=-2 -2x$
بتعويض  $x=-5$	$$\begin{gathered} f\text{'}\text{'}\left(-5\right)=-2 -2 \left(-5\right) \\ =-2 + 10 \\ =8>0 \end{gathered}$$
بتعويض $x=3$	$$\begin{gathered} f\text{'}\text{'}\left(3\right)=-2 -2 \left(3\right) \\ =-2 - 6 \\ =-8 <0 \end{gathered}$$

إذًا، بما أن  $f\text{'}\text{'}\left(-5\right)>0$، فإن للاقتران $f$ قيمة صغرى محلية عند $x=-5$ وهي:   $f\left(-5\right)=\frac{-115}{3}$، لأن

$$\begin{gathered} f\left(-5\right)=20 + 15\left(-5\right) - {\left(-5\right)}^2 - \frac{{\left(-5\right)}^3}{3} =20-75 -25 +\frac{125}{3} \\ = - 80 + \frac{125}{3}=\frac{-240}{3} + \frac{125}{3} =\frac{-115}{3} \end{gathered}$$

بما أن $f\text{'}\text{'}\left(3\right)<0$، فإن للاقتران $f$ قيمة عظمى محلية عند $x=3$ وهي: $f\left(3\right)=47$ ،  لأن $f\left(3\right)=20 + 15\left(3\right) - {\left(3\right)}^2 - \frac{{\left(3\right)}^3}{3} =20 + 45 - 9 - 9=47$ 

3) أستعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية (إن وجدت) للاقتران:$f\left(x\right)=x^4 - 2x^2 - 2$.

 

الحل:

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران.

الاقتران المعطى	$f\left(x\right)=x^4 - 2x^2 - 2$
أشتق الاقتران	$f \text{'}\left(x\right)=4x^3 - 4x$
بمساواة المشتقة بالصفر $f \text{'}\left(x\right)=0$	$4x^3 - 4x=0$
بقسمة طرفي المعادلة على $4$	$x^3 - x=0$
بتحليل المعادلة :إخراج $x$ عامل مشترك	$x\left(x^2 - 1\right)=0$
تحليل العبارة  $x^2 - 1$	$x \left(x - 1\right) \left(x +1\right)=0$
باستعمال خاصية الضرب الصفري	$x=0 or x - 1=0 or x + 1=0$
بحل المعادلتين	$x=1 or x=-1$

إذًا، القيمl الحرجة للاقتران $f$ هي: $x=0 , x=1 , x=-1$.

الخطوة 2: أجد المشتقة الثانية للاقتران.

المشتقة الأولى للاقتران	$f \text{'}\left(x\right)=4x^3 - 4x$
المشتقة الثانية للاقتران	$f\text{'}\text{'}\left(x\right)=12x^2 - 4$

الخطوة 3: أُعوض القيم الحرجة في المشتقة الثانية؛ لتحديد نوعها.

اقتران المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=12x^2 - 4$
بتعويض $x=0$	$$\begin{gathered} f\text{'}\text{'}\left(0\right)=12{\left(0\right)}^2 - 4 \\ =-4<0 \end{gathered}$$
بتعويض $x=1$	$$\begin{gathered} f\text{'}\text{'}\left(1\right)=12{\left(1\right)}^2 - 4 \\ =8 >0 \end{gathered}$$
بتعويض $x=-1$	$$\begin{gathered} f\text{'}\text{'}\left(-1\right)=12{\left(-1\right)}^2 - 4 \\ =12 - 4 \\ =8 >0 \end{gathered}$$

إذًا، بما أن $f\text{'}\text{'}\left(0\right)<0$، فإن للاقتران $f$ قيمة عظمى محلية عند $x=0$ وهي:   $f\left(0\right)=-2$، لأن        $f\left(0\right)={\left(0\right)}^4 - 2{\left(0\right)}^2 - 2=-2$

بما أن$f\text{'}\text{'}\left(1\right) >0$، فإن للاقتران $f$ قيمة صغرى محلية عند $x=1$ وهي: $f\left(1\right)=-3$، لأن $f\left(1\right)={\left(1\right)}^4 - 2{\left(1\right)}^2 - 2=-3$

إذًا، بما أن $f\text{'}\text{'}\left(-1\right) >0$، فإن للاقتران $f$ قيمة صغرى محلية عند $x=-1$ وهي: $f\left(-1\right)=-3$، لأن    $f\left(-1\right)={\left(-1\right)}^4 - 2{\left(-1\right)}^2 - 2=1 - 2 -2=-3$    

 

 

يُمثِّل الشكل المجاور مُخططًا لحديقة منزلية على شكل مستطيل أُنشئت مقابل جدار . إذا كان محيط الحديقة من دون الجدار $300 m$، فأجد كلاً مما يأتي:

4) المقدار الجبري الذي يُمثل طول الضلع AB بدلالة $x$.

5) اقتران مساحة الحديقة بدلالة $x$.

6) بُعدي الحديقة اللذين يجعلان مساحتها أكبر ما يُمكن.

الحل:

4) أفترض أن طول  الضلع $AB$ هو $y$ ، لكن طول الضلع $AB$  يساوي طول الضلع $CD$ من خصائص المستطيل

محيط الحديقة بدون الجدار $300 m$	$2y + x=300$
بكتابة $y$ بدلالة $x$ إضافة $-x$ لطرفي المعادلة	$2y=300 - x$
بقسمة طرفي المعادلة على $2$	$$\begin{gathered} y=\frac{300 - x}{2} \\ =150 - \frac{x}{2} \end{gathered}$$

إذًا،  $y=150 - \frac{x}{2}$.

5) أجد اقتران مساحة الحديقة بدلالة $x$.

اقتران مساحة الحديقة	$S=x y$
بتعويض $y=150 - \frac{x}{2}$	$$\begin{gathered} S\left(x\right)=x \left(150 - \frac{x}{2}\right) \\ =150x - \frac{x^2}{2} \end{gathered}$$

إذًا، اقتران مساحة الحديقة هو:   $S\left(x\right)=150x - \frac{x^2}{2}$.

6) أجد بُعدي الحديقة اللذين يجعلان مساحتها أكبر ما يُمكن.

الخطوة 1: أجد المشتقة والقيم الحرجة للاقتران.

اقتران مساحة الحديقة	$S\left(x\right)=150x - \frac{x^2}{2}$
أشتق اقتران مساحة الحديقة	$S\text{'}\left(x\right)=150 - x$
بمساواة المشتقة بالصفر $S\text{'}\left(x\right)=0$	$150 -x=0$
بحل المعادلة: إضافة $-150$ لطرفي المعادلة	$x=150$

إذًا، القيمة الحرجة لاقتران المساحة هي: $x=150$.

الخطوة 2: أجد المشتقة الثانية للاقتران.

مشتقة اقتران مساحة الحديقة	$S\text{'}\left(x\right)=150 - x$
المشتقة الثانية	$S\text{'}\text{'}\left(x\right)=-1$

الخطوة 3:استعمل اختبار المشتقة الثانية لتحديد نوع القيمة الحرجة .

إذًا، بما أن $S\text{'}\text{'}\left(x\right)=-1$ لجميع قيم $x$ الموجبة، فإن لاقتران المساحة قيمة عظمى محلية عند  $x=150$، أي أن المساحة أكبر ما يمكن عندما يكون طول الحديقة $150 m$، وعرضها  $75 m$ لأن:  $y=\frac{300-150}{2}=\frac{150}{2}=75$.

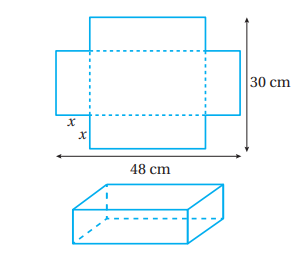
قطعة ورق مستطيلة الشكل، طولها $48 cm$، وعرضها $30 cm$.

قُصَّ من زوايا القطعة مربعات متطابقة، طول ضلع كل منها $x cm$ 

كما في الشكل المجاور، ثم ثُنيت لتشكيل عُلبة:

7) أجد الاقتران الذي يُمثل حجم العلبة بدلالة $x$.

8) أجد قيمة $x$ التي تجعل حجم العلبة  أكبر ما يمكن.

الحل: 

7) أجد اقتران الحجم بدلالة $x$.

اقتران حجم العلبة	$V=l \times w \times h$
بتعويض $l=48 - 2x ,w=30 - 2x , h=x$	$V\left(x\right)=\left(48 - 2x\right) \times \left(30 - 2x\right) \times \left(x\right)$
بالتبسيط	$$\begin{gathered} V\left(x\right)=\left(48 - 2x\right) \left(30x - 2x^2\right) \\ =1440x - 96x^2 - 60x^2 +4x^3 \\ =4x^3 -156x^2 + 1440x \end{gathered}$$

إذًا، اقتران حجم العلبة بدلالة $x$ هو: $V\left(x\right)=4x^3 -156x^2 + 1440x$.

 

8) أجد قيمة $x$ التي تجعل حجم العلبة  أكبر ما يمكن.

الحل: 

الخطوة 1: أجد المشتقة والقيم الحرجة لاقتران الحجم.

اقتران الحجم	$V\left(x\right)=4x^3 -156x^2 +1440x$
أشتق اقتران الحجم	$V\text{'}\left(X\right)=12x^2 -312x + 1440$
بمساواة المشتقة بالصفر $V\text{'}\left(x\right)=0$	$12x^2 - 312x + 1440=0$
بقسمة  طرفي المعادلة على $12$	$x^2 -26 + 120=0$
بتحليل المعادلة	$\left(x - 20\right)\left(x - 6\right)=0$
باستعمال خاصية الضرب الصفري	$x - 20=0 or x - 6=0$
بحل المعادلتين	$x=20 or x=6$

إذًا، القيم الحرجة لاقتران الحجم هي: $x=20 , x=6$.

الخطوة 2: أجد المشتقة الثانية للاقتران.

المشتقة الأولى للحجم	$V\text{'}\left(x\right)=12x^2 -312x + 1440$
المشتقة الثانية للحجم	$V\text{'}\text{'}\left(x\right)=24x - 312$

الخطوة 3:أُعوض القيم الحرجة في المشتقة لتحديد نوعها. 

اقتران المشتقة الثانية للحجم	$V\text{'}\text{'}\left(x\right)=24x -312$
بتعويض $x=20$	$$\begin{gathered} V \text{'}\text{'}\left(20\right)=24\left(20\right) - 312 \\ =480 - 312 \\ =168 >0 \end{gathered}$$
بتعويض $x=6$	$$\begin{gathered} V\text{'}\text{'}\left(6\right)=24\left(6\right) - 312 \\ =144 - 312 \\ =-168 <0 \end{gathered}$$

إذًا، بما أن $V\text{'}\text{'}\left(20\right) >0$، فإن لاقتران الحجم قيمة صغرى محلية عند $x=20$، وهذه القيمة تهمل لأن المطلوب قيمة عظمى محلية ( أكبر ما يمكن)

بما أن $V\text{'}\text{'}\left(6\right)<0$، فإن لاقتران الحجم قيمة عظمى محلية عند $x=6$ ؛ أي أن حجم العلبة يكون أكبر ما يمكن عندما $x=6$.

 

 

يُمثِّل الاقتران: $s\left(x\right)=500 - 0.002x$ سعر منتج لإحدى الشركات، حيث $x$ عدد القطع المنتجة . ويُمثِّل الاقتران: $C\left(x\right)=300 + 1.10x$ تكلفة إنتاج $x$ قطعة:

9) أجد اقتران الإيراد.

10)أجد اقتران الربح.

11) أجد عدد القطع اللازم بيعها من المنتج لتحقيق أكبر ربح ممكن، ثم أجد أكبر ربح ممكن.

12) أجد سعر الوحدة الواحدة  من المنتج الذي يحقق أكبر ربح ممكن.

 

9) أجد اقتران الإيراد.

الحل:

اقتران الإيراد  = السعر $\times$ الكمية	$R\left(x\right)=\left(500 -0.002x\right)\left(x\right)$
بالتبسيط	$R\left(x\right)=500x - 0.002x^2$

إذًا، اقتران الإيراد هو: $R\left(x\right)=500x - 0.002x^2$.

10) أجد اقتران الربح.

الحل:

اقتران الربح = اقتران الإيراد - اقتران التكلفة	$P\left(x\right)=R\left(x\right) - C\left(x\right)$
بتعويض: $R\left(x\right)=500x - 0.002x^2$$C\left(x\right)=300 + 1.10x$	$P\left(x\right)=\left(500x - 0.002x^2\right) - \left(300 + 1.10x\right)$
بالتبسيط	$$\begin{gathered} P\left(x\right)=500x - 0.002x^2 - 300 - 1.10x \\ =-0.002x^2 +498.9x - 300 \end{gathered}$$

إذًا، اقتران الربح هو: $P\left(x\right)=-0.002x^{2 }+ 498.9x - 300$.

11) أجد عدد القطع اللازم بيعها من المنتج لتحقيق أكبر ربح ممكن، ثم أجد أكبر ربح ممكن.

الحل:

الخطوة 1: أجد المشتقة والقيم الحرجة لاقتران الربح.

اقتران الربح	$P\left(x\right)=-0.002x^2 +498.9x -300$
اقتران الربح الحدي	$P\text{'}\left(x\right)=-0.004x + 498.9$
بمساواة المشتقة (الربح الحدي) بالصفر $P\text{'}\left(x\right)=0$	$-0.004x + 498.9=0$
بحل المعادلة: ضرب المعادلة ب $-1$	$0.004x - 498.9=0$
إضافة $498.9$ لطرفي المعادلة	$0.004x=498.9$
بقسمة طرفي المعادلة على $0.004$	$$\begin{gathered} x=\frac{498.9}{0.004}=124.725 \\ x\approx 125 \end{gathered}$$

إذًا، القيمة الحرجة للاقتران هي: $x=125$.

الخطوة 2: أجد المشتقة الثانية للاقتران.

اقتران الربح الحدي	$P\text{'}\left(x\right)=-0.004x + 498.9$
المشتقة الثانية للربح	$P\text{'}\text{'}\left(x\right)=-0.004$

الخطوة 3: استعمل اختبار المشتقة الثانية لتحديد نوع القيمة الحرجة .

إذًا، بما أن $P\text{'}\text{'}\left(x\right)<0$ لجميع قيم $x$ الموجبة، فإن لاقتران الربح قيمة عظمى محلية عند $x=125$؛ أي أن الربح أكبر ما يمكن عندما تبيع  الشركة $125$ قطعة من المنتج.

__  أجد أكبر ربح

اقتران الربح	$P\left(x\right)=-0.002x^2 +498.9x - 300$
بتعويض $x=125$	$P\left(125\right)=-0.002{\left(125\right)}^2 + 498.9\left(125\right) - 300$
بالتبسيط	$$\begin{gathered} P\left(125\right)=-31.25 + 62362.5 -300 \\ =62031.25 \end{gathered}$$

إذًا، أكبر ربح تحققه الشركة عندما تبيع $125$ قطعة هو: $62031.25$

12) أجد سعر الوحدة الواحدة  من المنتج الذي يحقق أكبر ربح ممكن.

الحل: 

سعر الوحدة الواحدة  من المنتج الذي يحقق أكبر ربح ممكن هو: $s\left(125\right)$

سعر بيع القطعة من المنتج $s\left(x\right)$	$s\left(x\right)=500 - 0.002x$
بتعويض $x=125$	$s\left(125\right)=500 - 0.002\left(125\right)$
بالتبسيط	$$\begin{gathered} s\left(125\right)=500 -0.25 \\ =499.75 \end{gathered}$$

إذًا، سعر الوحدة الواحدة  من المنتج الذي يحقق أكبر ربح هو: $499.75$.

 

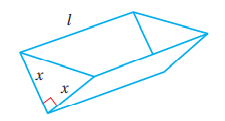
تحدي: قالب لصنع الكعك على شكل منشور ثلاثي مفتوح من الأعلى، قاعدته على شكل مثلث قائم

الزاوية كما في الشكل المجاور. إذا كان حجم القالب $1000 c{m}^3$، فأجد أبعاده التي

 تجعل المواد المُستعملة لصنعه أقل ما يُمكن، مبررًا إجابتي.

الحل:

الخطوة 1:  أكتب الاقتران الذي أُريد إيجاد قيمته القصوى  بدلالة متغير واحد.

اقتران المواد المُستعملة لصنعه هو اقتران المساحة الكلية لسطح المنشور الثلاثي بدون الوجه الأعلى.

•  أجد اقتران المساحة.

اقتران المساحة = مجموع مساحة المستطلين الجانبين + مجموع مساحة القاعدتين	$S=x l +x l+\frac{1}{2}{x}^2 +\frac{1}{2}{x}^2$
بالتبسيط	$S=2x l + x^2$

إذًا، اقتران المساحة هو: $S=2x l + x^2$.

• أكتب $l$ بدلالة $x$ باستعمال حجم المنشور.

اقتران حجم المنشور = مساحة القاعدة $\times$ الارتفاع	$V=\frac{1}{2}{x}^2 \times l$
بتعويض $v=1000$	$\frac{1}{2}{x}^2 l=1000$
بالتبسيط	$$\begin{gathered} x^2 l=2000 \\ l=\frac{2000}{x^2} \end{gathered}$$

إذًا، $l$ بدلالة $x$ هي: $l=\frac{2000}{x^2}$

• أُعوض $l$ في اقتران المساحة. 

اقتران المساحة	$S=2x l + x^2$
بتعويض $l=\frac{2000}{x^2}$	$S\left(x\right)=2x \left(\frac{2000}{x^2}\right) + x^2$
بالتبسيط	$S\left(x\right)=\frac{4000}{x} + x^2$

إذًا، اقتران المساحة بدلالة $x$ هو: $S\left(x\right)=\frac{4000}{x} + x^2$.

الخطوة 2: أجد المشتقة والقيم الحرجة لاقتران المساحة.

اقتران المساحة	$S\left(x\right)=\frac{4000}{x} + x^2$
اشتق اقتران المساحة	$S\text{'}\left(x\right)=\frac{-4000}{x^2} +2x$
بمساواة المشتقة بالصفر $S\text{'}\left(x\right)=0$	$\frac{-4000}{x^2} + 2x=0$
بحل المعادلة: إضافة $\frac{4000}{x^2}$ لطرفي المعادلة	$2x=\frac{4000}{x^2}$
بالضرب التبادلي ، وقسمة طرفي المعادلة على $2$، وأخذ الجذر التكعيبي لطرفي المعادلة	$$\begin{gathered} 2x^3=4000 \\ {x}^3=2000 \\ \sqrt[3]{x^3}=\sqrt[3]{2000} \\ x=\sqrt[3]{2000} \end{gathered}$$

إذًا، القيمة الحرجة لاقتران المساحة هي: $x=\sqrt[3]{2000}$,

الخطوة 3: أجد المشتقة الثانية لاقتران المساحة.

اقتران مشتقة المساحة	$S\text{'}\left(x\right)=\frac{-4000}{x^2} + 2x$
المشتقة الثانية لاقتران المساحة	$S\text{'}\text{'}\left(x\right)=\frac{-4000\left(-2x\right)}{{\left(x^2\right)}^2} +2$
بالتبسيط	$S\text{'}\text{'}\left(x\right)=\frac{8000}{x^3} + 2$

الخطوة 4: أُعوض القيمة الحرجة في المشتقة الثانية؛ لتحديد نوعها.

اقتران المشتقة الثانية للمساحة	$S\text{'}\text{'}\left(x\right)=\frac{8000}{x^3} + 2$
بتعويض $x=\sqrt[3]{2000}$	$S\text{'}\text{'}\left(\sqrt[3]{2000} \right)=\frac{8000}{{\left(\sqrt[3]{2000} \right)}^3} + 2$
بالتبسيط	$$\begin{gathered} S\text{'}\text{'}\left(\sqrt[3]{2000} \right)=\frac{8000}{{\left(\sqrt[3]{2000} \right)}^3} + 2 \\ =\frac{8000}{2000} + 2 \\ =4 + 2=6 >0 \end{gathered}$$

إذًا، بما أن $S\text{'}\text{'}\left(\sqrt[3]{2000} \right)>0$، فإن لاقتران المساحة قيمة صغرى محلية عند $x=\sqrt[3]{2000}$ ؛ أي أن كمية المادة المستخدمة في صنع القالب تكون أقل ما يمكن عندما تكون $x=\sqrt[3]{2000}=10\sqrt[3]{2} cm$ ، وتكون $l=\frac{2000}{{\left(\sqrt[3]{2000} \right)}^2} cm$.

كتاب التمارين ( صفحة 23)

1)أذا كان: $f\left(x\right)=2x^2+4x-3$، استعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية للاقتران(إن وجدت).

الحل: 

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران.

الاقتران المعطى	$f\left(x\right)=2x^2+4x-3$
المشتقة الأولى	$f\text{'}\left(x\right)=4x+4$
بتعويض $f\text{'}\left(x\right)=0$	$4x+4=0$
بحل المعادلة	$$\begin{gathered} 4x+4=0 \\ 4x=-4 \\ x=-1 \end{gathered}$$

إذًا، القيم الحرجة للاقتران $f$ هي: $x=-1$.

الخطوة 2: أجد المشتقة الثانية.

المشتقة الأولى	$f\text{'}\left(x\right)=4x+4$
المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=4$

الخطوة 3: أُعوض القيم الحرجة في المشتقة الثانية؛ لتحديد نوعها.

المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=4$
بتغويض$x=-1$	$f\text{'}\text{'}\left(-1\right)=4$

بما أن $f\text{'}\text{'}\left(-1\right)>0$، فإن للاقتران $f$ قيمة صغرى محلية عند $x=-1$ وهي: $f\left(-1\right)=-5$$f\left(-1\right)=2{\left(-1\right)}^2+4\left(-1\right)-3=-5$

2) إذا كان: $f\left(x\right)=x^3-5x^2+3x+1$، استعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية للاقتران(إن وجدت).

الحل:

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران.

الاقتران المعطى	$f\left(x\right)=x^3-5x^2+3x+1$
المشتقة الأولى	$f\text{'}\left(x\right)=3x^2-10x+3$
بتعويض $f\text{'}\left(x\right)=0$	$3x^2-10x+3=0$
بحل المعادلة	$$\begin{gathered} \left(3x-1\right)\left(x-3\right)=0 \\ 3x-1=0 or x-3=0 \\ x=\frac{1}{3} or x=3 \end{gathered}$$

إذًا، القيم الحرجة للاقتران $f$ هي: $x=\frac{1}{3} , x=3$.

الخطوة 2: أجد المشتقة الثانية.

المشتقة الأولى	$f\text{'}\left(x\right)=3x^2-10x+3$
المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=6x-10$

الخطوة 3: أُعوض القيم الحرجة في المشتقة الثانية؛ لتحديد نوعها.

المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=6x-10$
بتعويض $x=\frac{1}{3} , x=3$	$$\begin{gathered} f\text{'}\text{'}\left(\frac{1}{3}\right)=6\left(\frac{1}{3}\right)-10 \\ =2-10=-8<0 \\ f\text{'}\text{'}\left(3\right)=6\left(3\right)-10 \\ =18-10=8>0 \end{gathered}$$

إذًا، بما أن $f\text{'}\text{'}\left(\frac{1}{3}\right)<0$، فإن للاقتران $f$ قيمة عظمى محلية عند $x=\frac{1}{3}$ وهي: $f \left(\frac{1}{3}\right)=\frac{40}{27}$$$\begin{gathered} f \left(\frac{1}{3}\right)={\left(\frac{1}{3}\right)}^3-5{\left(\frac{1}{3}\right)}^2+3\left(\frac{1}{3}\right)+1 =\frac{1}{27}-\frac{5}{9}+1+1=\frac{1}{27}-\frac{5}{9}+2 \\ =\frac{1}{27}-\frac{15}{27}+\frac{54}{27}=\frac{40}{27} \end{gathered}$$

وبما أن $f\text{'}\text{'}\left(3\right)>0$، فإن للاقتران $f$ قيمة صغرى محلية عند $x=3$ وهي: $f\left(3\right)=-8$                  $f\left(3\right)={\left(3\right)}^3-5{\left(3\right)}^2+3\left(3\right)+1 =27-45+9+1=-8$

3) إذا كان: $f\left(x\right)=x^3 \left(x-2\right)$، استعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية للاقتران(إن وجدت).

 

الحل:

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران.

الاقتران المعطى	$f\left(x\right)=x^3 \left(x-2\right)$
بإعادة كتابة الاقتران	$f\text{'}\left(x\right)=x^4-2x^3$
المشتقة الأولى	$f\text{'}\left(x\right)=4x^3-6x^2$
بتعويض $f\text{'}\left(x\right)=0$	$4x^3-6x^2=0$
بحل المعادلة                                    إخراج العامل المشترك                  استعمال خاصية الضرب الصفري	$$\begin{gathered} 2x^2\left(2x-3\right)=0 \\ 2x^2=0 or 2x-3=0 \\ x=0 or x=\frac{3}{2} \end{gathered}$$

إذًا، القيم الحرجة للاقتران $f$ هي: $x=0 , x=\frac{3}{2}$.

الخطوة 2: أجد المشتقة الثانية.

المشتقة الأولى	$f\text{'}\left(x\right)=4x^3-6x^2$
المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=12x^2-12x$

الخطوة 3: أُعوض القيم الحرجة في المشتقة الثانية؛ لتحديد نوعها.

المشتقة الثانية	$f\text{'}\text{'}\left(x\right)=12x^2-12x$
بتعويض $x=0 , x=\frac{3}{2}$	$$\begin{gathered} f\text{'}\text{'}\left(0\right)=12{\left(0\right)}^2-12\left(0\right)=0 \\ f\text{'}\text{'}\left(\frac{3}{2}\right)=12{\left(\frac{3}{2}\right)}^2-12\left(\frac{3}{2}\right) \\ =12\left(\frac{9}{4}\right)-18 \\ =27-18=9>0 \end{gathered}$$

إذا، بما أن $f\text{'}\text{'}\left(\frac{3}{2}\right)>0$، فإن للاقتران $f$ قيمة صغرى محلية $x=\frac{3}{2}$ عند  هي:  $f \left(\frac{3}{2}\right)=\frac{-27}{16}$$$\begin{gathered} f \left(\frac{3}{2}\right)={\left(\frac{3}{2}\right)}^4-2{\left(\frac{3}{2}\right)}^3=\frac{81}{16}-2\left(\frac{27}{8}\right) \\ =\frac{81}{16}-\frac{54}{8}=\frac{81}{16}-\frac{108}{16} =\frac{-27}{16} \end{gathered}$$

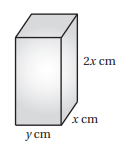
يُبيِّن الشكل المجاور  قالبًا يُستعمل لصنع لَبِنات البناء، وتبلغ مساحة سطحه الكلية $600 c{m}^2$:

4) أجد الاقتران الذي يُمثل حجم القالب بدلالة $x$.

5) أجد قيمة $x$ التي تجعل حجم القالب أكبر ما يُمكن.

الحل:

4)  حجم القالب = طول القاعدة$\times$عرض القاعدة $\times$ الارتفاع                                                                                                  $$\begin{gathered} V=y x 2x \\ V=2x^{2 }y \end{gathered}$$

• أكتب اقتران الحجم بمتغير واحد. 

اقتران المساحة الكلية	$$\begin{gathered} A=2\left(x\right)\left(2x\right)+2\left(y\right)\left(2x\right)+2\left(y\right)\left(x\right) \\ =4x^2+4yx+2yx \\ =4x^2+6yx \end{gathered}$$
بتعويض $A=600$	$4x^2+6yx=600$
بكتابة $y$ بدلالة $x$	$$\begin{gathered} 6yx=600-4x^2 \\ y=\frac{600-4x^2}{6x} \end{gathered}$$
بتعويض $y$ في اقتران الحجم	$V\left(x\right)=2x^2 \left(\frac{600-4x^2}{6x}\right)$
بالتبسيط	$$\begin{gathered} V\left(x\right)=\frac{600x-4x^3}{3} \\ =200x-\frac{4}{3}{x}^3 \end{gathered}$$

إذًا، اقتران الحجم بمتغير واحد هو: $V\left(x\right)=200x-\frac{4}{3}{x}^3$

5) الحل:

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران.

الاقتران المعطى	$V\left(x\right)=200x-\frac{4}{3}{x}^3$
المشتقة الأولى	$V \text{'}\left(x\right)=200-4x^2$
بتعويض $V \text{'}\left(x\right)=0$	$200-4x^2=0$
بحل المعادلة	$$\begin{gathered} 200-4x^2=0 \\ 200=4x^2 \\ {x}^2=50 \Rightarrow x=\sqrt{50} \\ x=5\sqrt{2} \end{gathered}$$

إذًا، القيمة الحرجة لاقتران الحجم هي: $x=5\sqrt{2}$.

الخطوة 2: أجد المشتقة الثانية.

اقتران المشتقة الأولى	$V \text{'}\left(x\right)=200-4x^2$
اقتران المشتقة الثانية	$V \text{'}\text{'}\left(x\right)=-8x$

الخطوة 3: أُعوض القيم الحرجة في المشتقة الثانية؛ لتحديد نوعها.

اقتران المشتقة الثانية	$V \text{'}\text{'}\left(x\right)=-8x$
بتعويض $x=5\sqrt{2}$	$$\begin{gathered} V \text{'}\text{'}\left(5\sqrt{2}\right)=-8\left(5\sqrt{2}\right) \\ =-40\sqrt{2}<0 \end{gathered}$$

إذًا، بما أن $V\text{'}\text{'}\left(5\sqrt{2}\right)<0$فإن لاقتران الحجم قيمة عظمى محلية عند $x=5\sqrt{2}$.أي أن حجم القالب يكون أكبر ما يمكن عند $x=5\sqrt{2}$.

يُمثِّل الاقتران: $s\left(x\right)=150-0.5x$ سعر البدلة الرجالية الذي حدَّدته شركة لإنتاج الملابس، حيث $x$ عدد البدلات المَبيعة. ويُمثِّل الاقتران: $C\left(x\right)=4000+0.25x^2$ تكلفة إنتاج $x$ بدلة:

6) أجد اقتران الإيراد.

7) أجد اقتران الربح.

8) أجد عدد البدلات اللازم بيعها لتحقيق أكبر ربح مُمكن، ثم أجد أكبر ربح مُمكن.

9) أجد سعر البدلة الواحدة الذي يُحقق أكبر ربح مُمكن.

الحل:

6) الإيراد  = السعر $\times$ الكمية

اقتران الإيراد	$R\left(x\right)=\left(150-0.5x\right) \times x$
بالتبسيط	$R\left(x\right)=150x-0.5x^2$

   إذًا، اقتران الإيراد هو: $R\left(x\right)=150x-0.5x^2$        

7) اقتران الربح= افتران الإيراد - اقتران التكلفة

اقتران الربح	$P\left(x\right)=\left(150x-0.5x^2\right)-\left(4000+0.25x^2\right)$
بالتبسيط	$$\begin{gathered} P\left(x\right)=150x-0.5x^2-4000-0.25x^2 \\ =-0.75x^2+150x-4000 \end{gathered}$$

إذًا، اقتران الربح هو:  $P\left(x\right)=-0.75x^2+150x-4000$,     

8) لإيجاد عدد البدلات التي يجب بيعها لتحقيق أكبر ربح 

الخطوة 1: أجد المشتقة الأولى والقيم الحرجة للاقتران.        

اقتران الربح	$P\left(x\right)=-0.75x^2+150x-4000$
المشتقة الأولى	$P\text{'}\left(x\right)=-1.5x+150$
بتعويض  $P\text{'}\left(x\right)=0$	$-1.5x+150=0$
بحل المعادلة	$$\begin{gathered} -1.5x+150=0 \\ 1.5x-150=0 \\ 1.5x=150 \\ x=\frac{150}{1.5}=100 \end{gathered}$$

إذًا، القيمة الحرجة لاقترلن الربح هي:  $x=100$

الخطوة 2: أجد المشتقة الثانية.

المشتقة الأولى	$P\text{'}\left(x\right)=-1.5x+150$
المشتقة الثانية	$P\text{'}\text{'}\left(x\right)=-1.5$

الخطوة 3: أُعوض القيم الحرجة في المشتقة الثانية؛ لتحديد نوعها.

بما أن $P\text{'}\text{'}\left(x\right)=-1.5<0$ لجميع قيم $x$ فإن لاقتران الربح قيمة عظمى محلية عند $x=100$ أي أن أكبر ربح يتحقق عندما يكون عدد البدلات المبيعة $100$.

أكبر ربح هو:  $P\left(100\right)=3500$: 

$$\begin{gathered} P\left(100\right)=-0.75{\left(100\right)}^2+150\left(100\right)-4000 \\ =-7500+15000-4000=3500 \end{gathered}$$

9) الحل:

بما أن سعر البدلة هو $s\left(x\right)=150-0.5x$، فإن سعر البدلة الواحدة الذي يحقق أكبر ربح هو: $s\left(100\right)=150-0.5\left(100\right)=100$

10) أرادت إحدى الشركات أن تصنع خزانات من الفولاذ الرقيق المُقاوم للصدأ على شكل متوازي مستطيلات، بجيث يكون كل منها مفتوحًا من الأعلى، وحجمه $500 m^3$، وقاعدتة مربعة الشكل. أجد الأبعاد التي تجعل مساحة سطح الخزان أقل ما يُمكن.

الحل:

الخطوة 1: أرسم مخططًا

أفترض أن طول قاعدة الخزان $x$ ، وعرضها $x$ وارتفاع الخزان $h$

الخطوة 2:  أكتب الاقتران الذي أُريد إيجاد قيمته القصوى  بدلالة متغير واحد.

اقتران مساحة سطح الخزان بدون الوجه الأعلى هو: $A=4xh+x^2$.

•  أكتب $h$ بدلالة $x$

 

حجم الخزان	$V=x^{2}h$
بتعويض $V=500$	$x^{2}h=500$
أكتب $h$ بدلالة  $x$	$h=\frac{500}{x^2}$
بتعويض $h=\frac{500}{x^2}$ في اقتران المساحة	$A=4x\left(\frac{500}{x^2}\right)+x^2$
بالتبسيط	$A\left(x\right)=\frac{2000}{x}+x^2$

الخطوة 3: أجد المشتقة الأولى والقيم الحرجة للاقتران. 

اقتران المساحة	$A\left(x\right)=\frac{2000}{x}+x^2$
المشتقة الأولى	$A\text{'}\left(x\right)=\frac{-2000}{x^2}+2x$
بتعويض $A\text{'}\left(x\right)=0$	$\frac{-2000}{x^2}+2x=0$
بحل المعادلة	$$\begin{gathered} \frac{-2000}{x^2}=-2x \Rightarrow \frac{2000}{x^2}=2x \\ 2x^3=2000 \Rightarrow x^3=1000 \\ x=10 \end{gathered}$$

إذًا، القيمة الحرجة لاقتران المساحة هي: $x=10$,

الخطوة 4: أجد المشتقة الثانية.

المشتقة الأولى	$A\text{'}\left(x\right)=\frac{-2000}{x^2}+2x$
المشتقة الثانية	$A\text{'}\text{'}\left(x\right)=\frac{2000\left(2x\right)}{{\left(x^2\right)}^2}+2$
بالتبسيط	$A\text{'}\text{'}\left(x\right)=\frac{400}{x^3}+2$

الخطوة5: أُعوض القيم الحرجة في المشتقة الثانية؛ لتحديد نوعها.

اقتران المشتقة الثانية	$A\text{'}\text{'}\left(x\right)=\frac{400}{x^3}+2$
بتعويض  $x=10$	$A\text{'}\text{'}\left(10\right)=\frac{400}{{\left(10\right)}^3}+2$
بالتبسيط	$$\begin{gathered} A\text{'}\text{'}\left(10\right)=\frac{400}{1000}+2 \\ =0.4+2=2.4>0 \end{gathered}$$

إذًا، بما أن  $A\text{'}\text{'}\left(10\right)>0$، فإن للاقتران قيمة صغرى محلية عند $x=10$; إي أن مساحة سطح الخزان ( ما عدا الوجه العلوي) أصغر ما يمكن عندما $x=10$.

طول قاعدة الخزان $10 m$ ، وعرضها $10 m$ ، وارتفاع الخزان $5 m$ ، لأن    $h=\frac{500}{{\left(10\right)}^2}=5 m$.