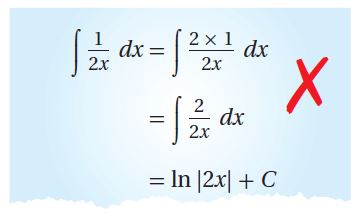الرياضيات فصل ثاني

حل أسئلة الدرس (5) تكامل اقترانات خاصة 

 

مسألة اليوم صفحة 42:

يتغير عدد الطلبة الذين يلتحقون بإحدى الجامعات الجديدة سنويًا بمعدل : $P\mathit{َ}\mathbf{ }\left(t\right) = \frac{500}{\sqrt{{\left(t+1\right)}^3}}$ ،

حيث $P\left(t\right)$ عدد الطلبة الملتحقين بالجامعة ، و $t$ الزمن بالسنوات منذ تأسيس الجامعة.

أجد عدد الطلبة الذين درسوا في الجامعة بعد 3 سنوات من تأسيسها،

علمًا بأن  عددهم عند تأسيس الجامعة بلغ 2000 طالب.

 

الحل:

الخطوة الأولى: أجد تكامل الاقتران $P \mathit{َ}\mathbf{ }\left(t\right)$ :

       $$\begin{gathered} P\mathit{َ}\mathbf{ }\left(t\right) = \frac{5000}{\sqrt{{(t+1)}^3}}=\frac{5000}{{\left(t+1\right)}^{{\displaystyle \frac{3}{2}}}} \\ P\left(t\right)=\int 5000 {(t+1)}^{-\frac{3}{2}} dt \\ = 5000\left(-2\right){\left(t+1\right)}^{-\frac{1}{2} }+C \\ =-10000 {(t+1)}^{-\frac{1}{2} }+C \end{gathered}$$

 

الخطوة الثانية: أجد ثابت التكامل C 

عدد طلاب الجامعة عند تأسيسها بلغ 2000 طالب، هذا يعني أنّ: $P\left(0\right)=2000$

                  $$\begin{gathered} P\left(t\right) = -10000{(t+1)}^{-\frac{1}{2}} + C \\ P\left(0\right) = -10000{(0+1)}^{-\frac{1}{2}} + C \\ 2000 = -10000 + C \\ \to C= 2000 + 10000 \\ C = 12000 \end{gathered}$$

 

الخطوة الثالثة:أجد عدد الطلبة الذين درسوا في الجامعة بعد 3 سنوات من تأسيسها:

      $$\begin{gathered} P\left(t\right) = -10000{(t+1)}^{-\frac{1}{2}} + 12000 \\ P\left(3\right) = -10000{(3+1)}^{-\frac{1}{2}} + 12000 \\ = -10000 {\left(4\right)}^{-\frac{1}{2}} +12000 \\ =\frac{-10000}{\sqrt{4}}+12000 \\ = \frac{-10000}{2}+12000 \\ = -5000 + 12000 \\ = 7000 \end{gathered}$$

إذن، عدد الطلبة الذين درسوا في الجامعة بعد 3 سنوات من تأسيسهاهو 7000 طالب.

---

أتحقق من فهمي صفحة 43:

أجد كلًا من التكاملات الآتية:

       $$\begin{gathered} a) \int (5x^2+7e^x\left)dx \\ b\right) \int (9\cos x+\frac{4}{x^3})dx \\ c) \int (\sqrt[3]{x}- \sin x) dx \end{gathered}$$

 

الحل:

$a) \int (5x^2+7e^x)dx =\frac{5}{3}{x}^3+7e^x+ C$	تكامل اقتران القوة، وتكامل الاقتران الأسي الطبيعي
$$\begin{gathered} b) \int (9\cos x+\frac{4}{x^3})dx =\int (9 \cos x+ 4x^{-3}) dx \\ = 9 \sin x + -\frac{4}{2}{x}^{-2} + C \\ = 9 \sin x - \frac{2}{x^2}+C \end{gathered}$$	تكامل اقتران جيب التمام، واقتران القوة ثم التبسيط
$$\begin{gathered} c) \int (\sqrt[3]{x}- \sin x) dx =\int \left(x^{\frac{1}{3}}-\sin x\right) dx \\ =\frac{x^{{\displaystyle \raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}}{{\displaystyle \frac{4}{3}}} +\cos x + C \\ =\frac{3}{4} \sqrt[3]{x^4} +\cos x + C \end{gathered}$$	تكامل اقتران القوة، واقتران الجيب ثم التبسيط

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

أتحقق من فهمي صفحة 45:

أجد كلًا من التكاملات الآتية:

    $$\begin{gathered} a) \int (\frac{1}{x}+8 e^x\left)dx \\ b\right) \int (\sin x-\frac{5}{x})dx \\ c) \int (\frac{x^2- 7 x + 2}{x^2}) dx \end{gathered}$$

 

الحل:

$a) \int (\frac{1}{x}+8 e^x)dx = \ln \left|x\right| + 8 e^x +C$	تكامل $\frac{1}{x}$، والاقتران الأسي الطبيعي
$b) \int (\sin x-\frac{5}{x})dx=-\cos x -5 \ln \left|x\right| +C$	تكامل اقتران الجيب، وتكامل $\frac{1}{x}$ المضروب في ثابت
$$\begin{gathered} c) \int (\frac{x^2- 7 x + 2}{x^2}) dx = \int \left(\frac{x^2}{x^2}- \frac{7x}{x^2}+\frac{2}{x^2}\right) dx \\ = \int \left(1-\frac{7}{x}+ 2x^{-2}\right)dx \\ = x -7 \ln \left|x\right| -\frac{2}{x}+C \end{gathered}$$	بقسمة كل حد في البسط على $x^2$ للتبسيط تكامل الثابت، وتكامل $\frac{1}{x}$المضروب في ثابت، وتكامل القوة

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

أتحقق من فهمي صفحة 47:

أجد كلًا من التكاملات الآتية:

                                      $$\begin{gathered} a) \int {(7x-5)}^6 dx b) \int \sqrt{2x+1}dx \\ c) \int 4\cos (3x-7) dx d) \int \left(\sin 5x +e^{2x}\right) dx \\ e) \int \left(6x^2 -3e^{7x+1}\right) dx f) \int \frac{5}{3x+2} dx \end{gathered}$$

 

الحل:

$$\begin{gathered} a) \int {(7x-5)}^6 dx = \frac{1}{\left(7\right)}\times \frac{1}{7}{(7x-5)}^7+C \\ =\frac{1}{49}{(7x-5)}^7+C \end{gathered}$$	تكامل ${(ax+b)}^n$
$$\begin{gathered} b) \int \sqrt{2x+1}dx=\int {\left(2x+1\right)}^{\frac{1}{2}} \\ = \frac{1}{2}\left(\frac{1}{{\displaystyle \frac{3}{2}}}\right){\left(2x + 1\right)}^{\frac{3}{2}} + C \\ = \frac{1}{3}\sqrt{{\left(2x+1\right)}^3} +C \end{gathered}$$	كتابة الاقتران بصورة أسية   تكامل اقتران القوة
$$\begin{gathered} c) \int 4\cos (3x-7) dx=\frac{1}{3} \times 4 \sin \left(3x-7\right) +C \\ = \frac{4}{3} \sin (3x-7) +C \end{gathered}$$	تكامل اقتران جيب التمام
$$\begin{gathered} d) \int (\sin 5x +e^{2x}) dx =\frac{1}{5}\times -\cos 5x +\frac{1}{2} e^{2x} + C \\ = -\frac{1}{5}\cos 5x +\frac{1}{2} e^{2x} + C \end{gathered}$$	تكامل اقتران الجيب ، والاقتران الأسي الطبيعي
$$\begin{gathered} e) \int (6x^2 -3e^{7x+1}) dx =\frac{6 x^3}{3}-\frac{3}{7}{e}^{7x+1} + C \\ = 2x^{3 }-\frac{3}{7}{e}^{7x+1} + C \end{gathered}$$	تكامل اقتران القوة، والاقتران الأسي الطبيعي
$f) \int \frac{5}{3x+2} dx=\frac{5}{3} \ln \left|3x+2\right|+C$	تكامل $\frac{1}{x}$ المضروب في ثابت

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

 

 

أتحقق من فهمي صفحة 49:

سكّان: أشارت دراسة إلى أن عدد السكان في إحدى القرى يتغير سنويًّا بمعدل يمكن نمذجته

            بالاقتران:$Pَ \left(t\right)=105 e^{0.03t}$ ، حيث $t$ عدد السنوات منذ عام 2010م ، و $P\left(t\right)$ عدد السكان.

            أجد عدد سكان القرية عام 2020م، علمًا بأنّ عدد سكانها عام 2010م هو 3500 شخص.

الحل:

الخطوة الأولى: جد تكامل الاقتران:$Pَ \left(t\right)$

                          $$\begin{gathered} P\left(t\right)=\int 105 e^{0.03t} dt \\ =\frac{105}{0.03} e^{0.03t} + C \\ =3500 e^{0.03t} + C \end{gathered}$$

 

الخطوة الثانية: أجد ثابت التكامل C:

 بما أن عدد سكان القرية عام 2010 هو 3500 شخص،

  فإن: $P\left(0\right)=3500 , t=0$

                                                $$\begin{gathered} P\left(0\right)=3500 e^{0.03\left(0\right)} + C \\ 3500 = 3500 e^0 + C \\ 3500=3500 + C \\ \to C=0 \end{gathered}$$

إذن الاقتران هو:$P\left(t\right)=3500 e^{0.03t}$

 

الخطوة الثالثة: أجد $P\left(10\right)$ حيث $t = 2020-2010 = 10$:

                         $$\begin{gathered} P\left(10\right)=3500 e^{0.03\left(10\right)} \\ = 3500 e^{0.3} \\ \approx 3500 \times 1.35 \\ = 4725 \end{gathered}$$

إذن عدد سكان القرية عام 2020م هو تقريبًا 4725 شخص.

---

أتحقق من فهمي صفحة 50:

أجد كلًّا من التكاملات الآتية:

$$\begin{gathered} a) \int \frac{2x+3}{x^2+3x}dx b) \int \frac{9x^2}{x^3+8}dx \\ c) \int \frac{x+1}{4x^2+8x}dx d) \int \frac{e^{3x}}{e^{3x}+5}dx \end{gathered}$$

الحل:

$a) \int \frac{2x+3}{x^2+3x}dx=\ln \left|x^2+3x\right|+C$	البسط يساوي مشتقة المقام
$$\begin{gathered} b) \int \frac{9x^2}{x^3+8}dx =3\int \frac{3x^2}{x^3+8}dx \\ =3 \ln \left|x^3+8\right| + C \end{gathered}$$	مشتقة المقام تساوي $\left(3x^2\right)$ لذلك يمكن كتابة البسط على الصورة: $9x^2=3\left(3x^2\right)$
$$\begin{gathered} c) \int \frac{x+1}{4x^2+8 x}dx =\int \frac{{\displaystyle \frac{1}{8}}\times 8\left(x+1\right)}{\left(4x^2+8 x\right)}dx \\ =\frac{1}{8}\int \frac{8x+8}{4x^2+8 x}dx \\ =\frac{1}{8}\ln \left|4x^2+8 x\right|+C \end{gathered}$$	مشتقة المقام تساوي$\left(8x+8\right)$ لذلك يمكن ضرب البسط وقسمته على 8 على الصورة: $x+1=\frac{1}{8}\times 8\left(x+1\right)$
$$\begin{gathered} d) \int \frac{e^{3x}}{e^{3x}+5}dx=\int \frac{{\displaystyle \frac{1}{3}}\left(3e^{3x}\right)}{e^{3x}+5}dx \\ =\frac{1}{3}\int \frac{3e^{3x}}{e^{3x}+5}dx \\ =\frac{1}{3}\ln \left|e^{3x}+5\right|+C \end{gathered}$$	مشتقة المقام تساوي$\left(3e^{3x}\right)$ لذلك يمكن ضرب البسط وقسمته على 3 على الصورة: $e^{3x}=\frac{1}{3}\left(3e^{3x}\right)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

أتحقق من فهمي صفحة 51:

أجد كلًّا من التكاملات الآتية:

          $$\begin{gathered} a) {\int }_0^2\left( 4e^{2x}+7\right) dx \\ b) {\int }_0^4\frac{1}{\sqrt{6x+1}} dx \\ c) {\int }_0^{4 }\frac{8x}{x^2+1}dx \end{gathered}$$

الحل:

   

$$\begin{gathered} a) {\int }_0^2( 4e^{2x}+7) dx=(\frac{4}{2}{e}^{2x}+7x) \overline{)\begin{array}{c}2\\ 0\end{array}} \\ =(2e^{2x}+7x) \overline{)\begin{array}{c}2\\ 0\end{array}} \\ =(2e^{2\left(2\right)}+7\left(2\right))-(2e^{2\left(0\right)}+7\left(0\right)) \\ =(2e^4+14)-(2e^0+0) \\ =2e^4+14-2 \\ =2e^4+12 \end{gathered}$$	تكامل الاقتران الأسي الطبيعي، وتكامل الثابت   تبسيط   تعويض
$$\begin{gathered} b) {\int }_0^4\frac{1}{\sqrt{6x+1}} dx={\int }_0^4{\left(6x+1\right)}^{-\frac{1}{2}} dx \\ =\frac{1}{6}\left(\frac{1}{{\displaystyle \frac{1}{2}}}\right){(6x+1)}^{\frac{1}{2}} \overline{)\begin{array}{c}4\\ 0\end{array}} \\ =\frac{2}{6}{(6x+1)}^{\frac{1}{2}} \overline{)\begin{array}{c}4\\ 0\end{array}} \\ =\frac{1}{3}\left[\sqrt{6\left(4\right)+1}-\sqrt{6\left(0\right)+1}\right] \\ =\frac{1}{3}\left[\sqrt{25}-\sqrt{1}\right] \\ =\frac{1}{3}\left[5-1\right] \\ =\frac{4}{3} \end{gathered}$$	الصورة الأسية   تكامل ${(ax+b)}^n$     تبسيط   تعويض بالصورة الجذرية
$$\begin{gathered} c) {\int }_0^{4 }\frac{8x}{x^2+1}dx =4 {\int }_0^4\frac{2x}{x^2+1}dx \\ =4 ln\left|x^2+1\right| \overline{)\begin{array}{c}4\\ 0\end{array} } \\ =4 \left[\left(ln\left|4^2+1\right|\right)-\left(ln\left|0^2+1\right|\right)\right] \\ =4\left[ln17-ln1\right] \\ = 4 ln 17 \end{gathered}$$	مشتقة المقام هي $2x$فأكتب : $8x=4 \left(2x\right)$ مشتقة $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$ تعويض تبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

أتدرب وأحل المسائل صفحة 52:

أجد كلًّا من التكاملات الآتية:

$1) \int \left(\frac{1}{2}{e}^x + 3x\right) dx=\frac{1}{2}{e}^x +\frac{3}{2}{x}^2 +C$	تكامل الاقتران الأسي الطبيعي، واقتران القوة
$$\begin{gathered} 2) \int (\frac{x^2+2x+1}{x^2})dx=\int (\frac{x^2}{x^2}+\frac{2x}{x^2}+\frac{1}{x^2})dx \\ = \int (1+\frac{2}{x}+x^{-2})dx \\ =x +2 \ln \left|x\right|-x^{-1}+C \\ =x+ 2 \ln \left|x\right|-\frac{1}{x}+C \end{gathered}$$	تكامل اقتران القوة وتكامل $\frac{1}{x}$ المضروب في ثابت
$$\begin{gathered} 3) \int {\left(e^x+1\right)}^2 dx=\int \left(e^{2x}+2e^x+1\right)dx \\ = \frac{1}{2}{e}^{2x}+2e^x+x+C \end{gathered}$$	تكامل الاقتران الأسي الطبيعي، واقتران الثابت
$$\begin{gathered} 4) \int \frac{1}{x} \left(x+2\right) dx=\int \left(\frac{x}{x}+\frac{2}{x}\right)dx \\ =\int \left(1+\frac{2}{x}\right)dx \\ =x+2\ln \left|x\right|+C \end{gathered}$$	إيجاد $\frac{1}{x}(x+2)$ثم تبسيط تكامل الثابت، وتكامل $\frac{1}{x}$المضروب في ثابت
$$\begin{gathered} 5) \int (\frac{4}{x^3}+\frac{5}{x}) dx=\int (4x^{-3}+\frac{5}{x})dx \\ =\frac{4}{-2}{x}^{-2}+5\ln \left|x\right|+C \\ =-\frac{2}{x^2}+5\ln \left|x\right|+C \end{gathered}$$	تكامل اقتران القوة $\frac{1}{x}$، وتكامل المضروب في ثابت
$$\begin{gathered} 6) \int \left(\sqrt{x} + 3 e^{6x} - \frac{7}{x}\right) dx \\ =\frac{2}{3}{x}^{\frac{3}{2}}+\frac{3}{6}{e}^{6x}-7\ln \left|x\right|+C \\ =\frac{2}{3}\sqrt{x^3}+\frac{1}{2}{e}^{6x}-7\ln \left|x\right|+C \end{gathered}$$	تكامل القوة، والاقتران الأسي الطبيعي، وتكامل $\frac{1}{x}$ المضروب في ثابت تحويل إلى الصورة الجذرية
$7) \int \left(\frac{3}{x+1}-5e^{-2x}\right)dx=3 \ln \left|x+1\right|+\frac{5}{2}{e}^{-2x}+C$	تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$، والاقتران الأسي الطبيعي
$$\begin{gathered} 8) \int \frac{1}{\sqrt{2x-3}}dx=\int {\left(2x-3\right)}^{-\frac{1}{2}} dx \\ =\left(2\right)\left(\frac{1}{2}\right){\left(2x-3\right)}^{\frac{1}{2}} +C \\ =\sqrt{2x-3} +C \end{gathered}$$	الصورة الأسية وتكامل اقتران القوة
$$\begin{gathered} 9) \int \left(\sin (2x-3) +e^{6x-4}\right) dx \\ =-\frac{1}{2}\cos (2x-3) +\frac{1}{6}{e}^{6x-4}+C \end{gathered}$$	تكامل اقتران الجيب ، والاقتران الأسي الطبيعي
$$\begin{gathered} 10) \int 4 cos\left(6x+1\right) dx=\frac{4}{6}\sin \left(6x+1\right)+C \\ =\frac{2}{3}\sin (6x+1)+C \end{gathered}$$	تكامل اقتران جيب التمام
$$\begin{gathered} 11) \int \frac{\sin x + 3 \cos x}{4} dx=\frac{1}{4}\left(-\cos x +3\sin x\right)+C \\ =-\frac{1}{4}\cos x +\frac{3}{4}\sin x + C \end{gathered}$$	تكامل اقتران الجيب وجيب التمام
$$\begin{gathered} 12) \int \left(e^{6x}+{\left(1-2x\right)}^6\right) dx=\frac{1}{6}{e}^{6x} -\frac{1}{\left(2\right)\left(7\right)}{(1-2x)}^7 +C \\ =\frac{1}{6}{e}^{6x} -\frac{1}{14}{(1-2x)}^7 +C \end{gathered}$$	تكامل الاقتران الأسي الطبيعي، وتكامل اقتران القوة
$$\begin{gathered} 13) \int \frac{x}{x^2+1} dx=\frac{1}{2}\int \frac{2x}{x^2+1}dx \\ = \frac{1}{2}ln\left|x^2+1\right|+C \end{gathered}$$	ضرب البسط والمقام بالعدد 2 تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$
$$\begin{gathered} 14) \int \frac{x^2}{x^3-1} dx=\frac{1}{3}\int \frac{3x^2}{x^3-1}dx \\ =\frac{1}{3}ln\left|x^3-1\right|+C \end{gathered}$$	ضرب البسط والمقام بالعدد 3 تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$
$$\begin{gathered} 15) \int \frac{x^2-x}{2x^3-3x^2+12} dx=\frac{1}{6}\int \frac{6\left(x^2-x\right)}{2x^3-3x^2+12}dx \\ =\frac{1}{6}\int \frac{6x^2-6x}{2x^3-3x^2+12}dx \\ =\frac{1}{6}ln \left|2x^3-3x^2+12\right|+C \end{gathered}$$	ضرب البسط والمقام بالعدد 6 تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$
$$\begin{gathered} 16) \int \frac{e^x+7}{e^x} dx=\int \left(\frac{e^x}{e^x}+\frac{7}{e^x}\right)dx \\ =\int \left(1+7 e^{-x}\right)dx \\ =x -7e^{-x}+C \\ = x -\frac{7}{e^x}+C \end{gathered}$$	بقسمة كل حد في البسط على $e^x$  تبسيط، واستعمال قوانين الأسس (الأس السالب) تكامل الثابت، والقوة
$$\begin{gathered} 17) \int \frac{1}{5-{\displaystyle \frac{1}{4}}x} dx=\int \frac{-4\left(-{\displaystyle \frac{1}{4}}\right)}{5-\frac{1}{4}x}dx \\ =-4\int \frac{-{\displaystyle \frac{1}{4}}}{5-{\displaystyle \frac{1}{4}}x} dx \\ = -4 ln\left|5-\frac{1}{4}x\right|+C \end{gathered}$$	ضرب البسط والمقام في العدد $\frac{-1}{4}$   تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$
$$\begin{gathered} 18) \int \left(4x^3+2+3 \sin \left(5-3x\right)\right) dx \\ =\frac{4x^4}{4}+2x -\frac{3}{-3} \cos (5-3x)+C \\ = x^{4 }+2x + \cos (5-3x)+C \end{gathered}$$	تكامل الاقترانات: القوة، والثابت، وجيب الزاوية
$$\begin{gathered} 19) \int \frac{e^{2x}}{e^{2x}+3} dx=\int \frac{{\displaystyle \frac{1}{2}}\left(2 e^{2x}\right)}{e^{2x}+3} dx \\ = \frac{1}{2}ln \left|e^{2x}+3\right|+ C \end{gathered}$$	الضرب والقسمة على العدد $\frac{1}{2}$ تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$
$$\begin{gathered} 20) \int \frac{3}{{\left(1-4x\right)}^2} dx=\int 3{\left(1-4x\right)}^{-2} dx \\ =\frac{3}{\left(-4\right)\left(-1\right)}{\left(1-4x\right)}^{-1}+C \\ =\frac{3}{4(1-4x)}+C \end{gathered}$$	قانون الأس السالب تكامل اقتران القوة قانون الأس السالب
$$\begin{gathered} 21) \int \frac{1+ x{e}^x}{x} dx=\int \left(\frac{1}{x}+\frac{x e^x}{x}\right) dx \\ = \int \left(\frac{1}{x}+e^x\right) dx \\ =ln \left|x\right|+e^x+C \end{gathered}$$	بقسمة كل حد في البسط على $x$ تبسيط تكامل الاقتران الأسي الطبيعي، وتكامل $\frac{1}{x}$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

 

 

 

 

 

 

 

 

 

أجد قيمة كلٍّ من التكاملات الآتية:

$$\begin{gathered} 22) {\int }_1^{2 }(2x + 3e^x-\frac{4}{x}) dx=\left(\frac{2x^2}{2}+3e^x - 4 \ln \left|x\right|\right) \overline{)\begin{array}{c}2\\ 1\end{array}} \\ =\left(x^2+3e^x - 4 \ln \left|x\right|\right) \overline{)\begin{array}{c}2\\ 1\end{array}} \\ =\left({\left(2\right)}^2+3e^2 - 4 \ln \left|2\right|\right)-\left({\left(1\right)}^2+3e^1 - 4 \ln \left|1\right|\right) \\ =\left(4+3e^2 - 4 \ln 2\right)-\left(1+3e-0\right) \\ =4+3e^2 - 4 \ln 2 -1-3e \\ =3+3e^2 -3e- 4 \ln 2 \end{gathered}$$	تكامل القوة، والأسي الطبيعي، وتكامل $\frac{1}{x}$ تعويض حدود التكامل تبسيط
$$\begin{gathered} 23) {\int }_0^{5 }\frac{x}{x^2+10} dx={\int }_0^{5 }\frac{{\displaystyle \frac{1}{2}}\left(2x\right)}{x^2+10}dx \\ =\frac{1}{2}{\int }_0^{5 }\frac{{\displaystyle 2x}}{x^2+10}dx \\ =\left(\frac{1}{2}\ln \left|x^2+10\right|\right) \overline{)\begin{array}{c}5\\ 0\end{array}} \\ =\frac{1}{2}\left(\ln |5^2+10|-\ln |0^2+10|\right) \\ =\frac{1}{2}\left(\ln |25+10|-\ln \left|10\right|\right) \\ =\frac{1}{2}\left(\ln 35-\ln 10\right) \\ =\frac{1}{2}\ln 35-\frac{1}{2}\ln 10 \end{gathered}$$	ضرب البسط والمقام بالعدد 2     تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$   تعويض حدود التكامل   تبسيط
$$\begin{gathered} 24) {\int }_3^{4 }{(2x -6)}^4 dx=\frac{1}{\left(2\right)\left(5\right)}{\left(2x-6\right)}^5 \overline{)\begin{array}{c}4\\ 3\end{array}} \\ =\frac{1}{10}{(2x-6)}^5 \overline{)\begin{array}{c}4\\ 3\end{array}} \\ =\frac{1}{10}\left[{(2\left(4\right)-6)}^5-{(2\left(3\right)-6)}^5\right] \\ =\frac{1}{10}[{(8-6)}^5-{(6-6)}^5] \\ =\frac{1}{10}[{\left(2\right)}^5-{\left(0\right)}^5] \\ =\frac{1}{10}\left({\left(2\right)}^5\right)=\frac{1}{10}\left(32\right)=\frac{32}{10}=\frac{16}{5} \end{gathered}$$	تكامل اقتران القوة تبسيط تعويض حدود التكامل تبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

25) يتحرك جسيم في مسار مستقيم، وتُعطى سرعته المتجهة بالاقتران: $v\left(t\right)= e^{-2t}$،

      حيث $t$ الزمن بالثواني، و $v$سرعته المتجهة بالمتر لكل ثانية.

     إذا كان الموقع الابتدائي للجسيم $2 m$ ، فأجد موقع الجسيم بعد $t$ ثانية من بدء الحركة.

 

الحل:

الخطوة الأولى: أجد اقتران الموقع $s\left(t\right)$

$s\left(t\right) = \int v\left(t\right) dt$	بإيجاد تكامل اقتران السرعة المتجهة
$= \int e^{-2t} dt$	بتعويض$v\left(t\right)= e^{-2t}$
$=\frac{1}{-2}{e}^{-2t} +C$	تكامل الاقتران الأسي الطبيعي

 

 

 

 

 

 

 

 

 

 

الخطوة الثانية: أجد قيمة ثابت التكامل $C$:

$s\left(t\right)=-\frac{1}{2}{e}^{-2t} +C$	اقتران الموقع
$$\begin{gathered} s\left(0\right)=-\frac{1}{2}{e}^{-2\left(0\right)} +C \\ 2 = -\frac{1}{2}+C \end{gathered}$$	الموقع الابتدائي يعني$s\left(0\right)$ بتعويض$t=0 , s\left(0\right) = 2$
$C=2+\frac{1}{2}=\frac{5}{2}$	بحل المعادلة

 

 

 

 

 

 

 

 

 

 

 

الخطوة الثالثة: أكتب اقتران الموقع $s\left(t\right)$

اقتران الموقع بعد t ثانية من بدء الحركة هو: $s\left(t\right)=-\frac{1}{2}{e}^{-2t} +\frac{5}{2}$

---

في كل مما يأتي المشتقة الأولى للاقتران $f\left(x\right)$ ، ونقطة يمر بها منحنى $y=f\left(x\right)$.

أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران $f\left(x\right)$:

 

$26) f\mathit{َ}\mathbf{ }(x)= 5 e^x ; (0 , \frac{1}{2})$                           

 

الحل:

الخطوة الأولى:أجد تكامل المشتقة الأولى:

                                                          $$\begin{gathered} f\left(x\right) = \int 5e^x dx \\ = 5e^x+C \end{gathered}$$

الخطوة الثانية : أجد ثابت التكامل C ، بتعويض النقطة $(0 , \frac{1}{2})$:

                                                            $$\begin{gathered} f\left(0\right)=5e^0+C \\ \frac{1}{2} = 5+C \end{gathered}$$

الخطوة الثالثة :أكتب قاعدة الاقتران $f\left(x\right)$

                                                          $f\left(x\right) = 5e^x-\frac{9}{2}$

---

$27) f\mathit{َ}\mathbf{ }(x)=\frac{2}{x}-\frac{1}{x^2} ; \left(1 , -1\right)$                          

الحل: 

الخطوة الأولى:أجد تكامل المشتقة الأولى:

                                                         $$\begin{gathered} f\left(x\right) = \int \left(\frac{2}{x}-\frac{1}{x^2}\right) dx \\ =2 \ln \left|x\right|+\frac{1}{x}+C \end{gathered}$$

الخطوة الثانية :أجد ثابت التكامل C ، بتعويض النقطة $(1 , -1)$

                            $$\begin{gathered} f\left(1\right)=2 \ln \left|1\right|+\frac{1}{1}+C \\ -1 =2 \ln 1 +1 + C \\ -1 =1 + C \\ \to C=-2 \end{gathered}$$

الخطوة الثالثة :أكتب قاعدة الاقتران $f\left(x\right)$

                           $f\left(x\right)=2 \ln \left|x\right|+\frac{1}{x}-2$

---

                         $28) f\mathit{َ}\mathbf{ }(x)=e^{-x} +x^2; (0 , 4)$

الحل:

الخطوة الأولى:أجد تكامل المشتقة الأولى:

                          $$\begin{gathered} f\left(x\right) = \int \left(e^{-x}+x^2\right) dx \\ = -e^{-x}+\frac{x^3}{3}+C \end{gathered}$$

الخطوة الثانية :أجد ثابت التكامل C ، بتعويض النقطة $(0 , 4)$

                                                            $$\begin{gathered} f\left(0\right)= -e^{-\left(0\right)}+\frac{0}{3}+C \\ 4 = -1 + C \\ \to 4+1=5=C \end{gathered}$$

 

الخطوة الثالثة :أكتب قاعدة الاقتران $f\left(x\right)$

                                                                $f\left(x\right)=-e^{-x}+\frac{1}{3}{x}^3+5$

---

29) إذا كان ميل المماس لمنحنى العلاقة $y$ هو:$\frac{dy}{dx}=2x +\frac{3}{x + e}$ ،

      فأجد قاعدة العلاقة $y$، علمًا بأن منحناها يمر بالنقطة $\left(e , e^2\right)$

الحل:

الخطوة الأولى:أجد تكامل المشتقة :

                $$\begin{gathered} y = \int \left(2x +\frac{3}{x + e}\right) dx \\ =\frac{2x^2}{2}+3 \ln \left|x+e\right|+C \\ =x^2 +3 \ln \left|x+e\right|+C \end{gathered}$$

الخطوة الثانية :أجد ثابت التكامل C ، بتعويض النقطة $(e , e^2)$

                         $$\begin{gathered} f\left(e\right)=e^2 +3 \ln |e+e|+C \\ e^2 =e^2 + 3 \ln 2e + C \\ {e}^2 -e^2 = 3 \ln 2e + C \\ 0= 3 \ln 2e + C \\ \to C=-3 \ln 2e \end{gathered}$$

الخطوة الثالثة :أكتب قاعدة العلاقة $y$:

         $y=x^2 +3 \ln |x+e|-3 \ln 2e$

---

بيئة: في دراسة تناولت أسماكًا في بحيرة، تبين أن عدد الأسماك $P\left(t\right)$ يتغير بمعدل:

       $P\mathit{َ}\mathbf{ }\left(t\right) = - 0.51 e^{-0.03t}$ ، حيث$t$ الزمن بالسنوات بعد بدء الدراسة:

30) أجد قاعدة الاقتران $P\left(t\right)$ عند أي زمن$t$ ، علمًا بأن عدد الأسماك عند بدء الدراسة هو 1000 سمكة.

 الحل:

الخطوة الأولى:أجد تكامل المشتقة :

            $$\begin{gathered} P\left(t\right) =\int - 0.51 e^{-0.03t} dt \\ =\frac{-0.51}{-0.03} e^{-0.03t} +C \\ =17 e^{-0.03t} +C \end{gathered}$$

الخطوة الثانية :أجد ثابت التكامل C ، بتعويض النقطة $\left(0, 1000\right)$

              $$\begin{gathered} P\left(0\right)=17 e^{-0.03\left(0\right)} +C \\ 1000=17+C \\ C=1000-17 \\ \to C= 983 \end{gathered}$$

الخطوة الثالثة :أكتب قاعدة الاقتران $P\left(t\right)$:

                           $P\left(t\right)=17 e^{-0.03t} +983$

 

31) أجد عدد الأسماك بعد 10 سنوات من بدء الدراسة.

                                 $$\begin{gathered} P\left(10\right)=17 e^{-0.03\left(10\right)} +983 \\ =17 e^{-0.3} + 983 \\ \approx 12.6 + 983 \\ \approx 995.6 \end{gathered}$$

إذن عدد الأسماك بعد 10 سنوات من بدء الدراسة تقريبًا: 996 سمكة .

---

طب: يلتئم جرح جلدي بمعدل يمكن نمذجته بالاقتران: $A\mathit{َ}\mathbf{ }\left(t\right) = - 0.9 e^{-0.1 t}$،

         حيث $t$ عدد الأيام بعد الإصابة بالجرح، و $A\left(t\right)$ مساحة سطح الجرح بالسنتيمتر المربع:

    

32) أجد قاعدة الاقتران $A\left(t\right)$ عند أي زمن $t$، علمًا بأن مساحة سطح الجرح عند الإصابة هي $9 c{m}^2$

الحل:

الخطوة الأولى:أجد تكامل المشتقة :

                                                     $$\begin{gathered} A\left(t\right) =\int - 0.9 e^{-0.1 t} dt \\ = \frac{-0.9}{-0.1} e^{-0.1 t} +C \\ =9 e^{-0.1 t} +C \end{gathered}$$

 

 

الخطوة الثانية :أجد ثابت التكامل C ، بتعويض: $t=0 , A\left(0\right)=9$

                        $$\begin{gathered} A\left(0\right)=9 e^{-0.1 \left(0\right)} +C \\ 9 =9+C \\ \to C=0 \end{gathered}$$

الخطوة الثالثة :أكتب قاعدة الاقتران $A\left(t\right)$:

                         $A\left(t\right)=9 e^{-0.1 t}$

 

33) أجد مساحة سطح الجرح بعد 5 أيام من الإصابة.

                                                $$\begin{gathered} A\left(5\right)=9 e^{-0.1\left( 5\right)} \\ = 9 e^{-0.5} \\ \approx 5.4588 \end{gathered}$$

إذن مساحة سطح الجرح بعد 5 أيام من الإصابة تقريبًا هو $5.5 c{m}^2$

---

مهارات التفكير العليا:

34) أكتشف الخطأ: أوجد أحمد ناتج التكامل: $\int \frac{1}{2x} dx$ ، وكان حله على النحو الآتي:

 أكتشف الخطأ في حل أحمد، ثم أصححه.

الحل:

الخطأ:ضرب البسط في (2) فقط، رغم أن $\frac{1}{2}$ ثابت

          ويمكن كتابة: $\int \frac{1}{2x} dx$ على الصورة: $\frac{1}{2}\int \frac{1}{x} dx$

الحل الصحيح:

                  $$\begin{gathered} \int \frac{1}{2x} dx =\frac{1}{2}\int \frac{1}{x} dx \\ = \frac{1}{2}\ln \left|x\right| + C \end{gathered}$$

---

تحدٍّ: أجد كل تكامل مما يأتي:

         $$\begin{gathered} 35) \int \sqrt{e^x} dx 36) \int \frac{\cos x}{3+ 2 \sin x} dx \\ 37) \int {\left(x^2+2x+1\right)}^5 dx \end{gathered}$$  

 

 

الحل:

$$\begin{gathered} 35) \int \sqrt{e^x} dx=\int {\left(e^x\right)}^{\frac{1}{2}} dx \\ =\int e^{\frac{1}{2}x} dx \\ =2 e^{\frac{1}{2}x} +C \end{gathered}$$	الصورة الأسية للجذر التربيعي   قوانين الأسس تكامل الاقتران الأسي الطبيعي
$$\begin{gathered} 36) \int \frac{\cos x}{3+ 2 \sin x} dx=\int \frac{{\displaystyle \frac{1}{2}}\left(2\cos x\right)}{3+ 2 \sin x} dx \\ =\frac{1}{2}\int \frac{2 \cos x}{3+ 2 \sin x} dx \\ =\frac{1}{2} \ln \left|3+ 2 \sin x\right|+C \end{gathered}$$	ضرب الاقتران في العدد 2 والقسمة عليه     تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$
$$\begin{gathered} 37) \int {(x^2+2x+1)}^5 dx=\int {\left({\left(x+1\right)}^2\right)}^5 dx \\ =\int {\left(x+1\right)}^{10} dx \\ = \frac{1}{11}{\left(x+1\right)}^{11} +C \end{gathered}$$	استعمال  تحليل المقدار المربع الكامل قوانين الأسس تكامل اقتران القوة

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

38) أكتشف المختلف: أيُّ التكاملات الآتية مختلف، مبررًا إجابتي؟ 

$\int \frac{1}{{\left(x+1\right)}^2} dx$

$\int \frac{1}{\sqrt{x-1}} dx$

$\int \frac{1}{x+1}dx$

$\int {\left(x-1\right)}^3 dx$

الحل:

التكامل المختلف هو: $\int \frac{1}{x+1}dx$ لأنه الوحيد الذي يُحل باللوغاريتم الطبيعي.

 

أما التكاملات الثلاث الأخرى فتُحل باستخدام القاعدة:

$\int {(ax +b)}^n dx = \frac{1}{a(n+1)}{(ax +b)}^{n+1}+C , n\ne -1$

---

كتاب التمارين صفحة 13:

أجد كلًّا من التكاملات الآتية:

 

       

$$\begin{gathered} 1) \int \frac{1-x^2}{5x} dx =\int \left(\frac{1}{5x}-\frac{x^2}{5x}\right)dx \\ =\frac{1}{5}\int \frac{1}{x}-\frac{1}{5}\int x dx \\ = \frac{1}{5}\ln \left|x\right|-\frac{1}{10}{x}^2 +C \end{gathered}$$	قسمة كل حد في البسط على $5x$   تكامل القوة وتكامل $\frac{1}{x}$
$2) \int \left(5 e^x + 4\right) dx =5 e^x+ 4x +C$	ت كامل الاقتران الأسي الطبيعي، وتكامل الثابت
$3) \int \left(1- e^{2x-3}\right) dx =x -\frac{1}{2}{e}^{2x-3} +C$	تكامل الثابت وتكامل الاقتران الأسي الطبيعي.
$$\begin{gathered} 4) \int (\sin 2x -\cos 2x) dx \\ =-\frac{1}{2}\cos 2x -\frac{1}{2}\sin 2x +C \end{gathered}$$	تكامل اقتراني الجيب، وجيب التمام
$$\begin{gathered} 5) \int \frac{3}{2x-1} dx =3\int \frac{{\displaystyle \frac{1}{2}\left(2\right)}}{2x-1}dx \\ =\frac{3}{2}\int \frac{2}{2x-1}dx \\ =\frac{3}{2}\ln |2x-1|+C \end{gathered}$$	ضرب الاقتران بالعدد  2 والقسمة عليه   تكامل الاقتران $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$
$$\begin{gathered} 6) \int \left(5 - \sin (5-5x)\right) dx \\ = 5x -\frac{1}{5}\cos (5-5x)+C \end{gathered}$$	تكامل الثابت، واقتران الجيب
$$\begin{gathered} 7) \int \frac{1}{{\displaystyle \frac{1}{3}}x-2} dx =\int \frac{3 \times \left({\displaystyle \frac{1}{3}}\right)}{\frac{1}{3}x-2}dx \\ = 3\int \frac{{\displaystyle \frac{1}{3}}}{\frac{1}{3}x-2}dx \\ = 3 \ln \left|\frac{1}{3}x-2\right|+C \end{gathered}$$	ضرب الاقتران بالعدد $\frac{1}{3}$ والقسمة عليه         تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$
$$\begin{gathered} 8) \int \left(2x-1+\frac{8}{5x+4}\right) dx \\ =\frac{2x^2}{2}-x+8\int \frac{{\displaystyle \frac{1}{5}\times 5}}{5x+4} dx \\ =x^2 - x +\frac{8}{5} \ln \left|5x+4\right|+C \end{gathered}$$	تطبيق قواعد التكامل (اقتران القوة)، الضرب بالعدد 5 والقسمة عليه   تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$
$9) \int \left(3 \cos x+\frac{5}{x}+\frac{4}{x^2}\right) dx =3 \sin x +5 \ln \left|x\right|-\frac{4}{x}+C$	تكامل اقترنات جيب التمام، والقوة، وتكامل $\frac{1}{x}$
$10) \int {\left(3x+2\right)}^5 dx =\frac{1}{18}{(3x+2)}^6 +C$	تكامل اقتران القوة
$$\begin{gathered} 11) \int \frac{x+1}{x^2+2x +5} dx =\frac{1}{2}\int \frac{2\left(x+1\right)}{x^2+2x +5} dx \\ =\frac{1}{2}\int \frac{2x+2}{x^2+2x +5} dx \\ = \frac{1}{2}\ln \left|x^2+2x +5\right|+C \end{gathered}$$	ضرب الاقتران بالعدد 2  وقسمته عليه ثم تكامل $\frac{f\text{'}\left(x\right)}{f\left(x\right)}$
$$\begin{gathered} 12) \int \left( e^{2x} -\frac{1}{2}\sin \left(2x-1\right)\right) dx \\ =\frac{1}{2}{e}^{2x} +\frac{1}{4} \cos (2x-1)+C \end{gathered}$$	تكامل الاقتران الأسي الطبيعي، واقتران جيب الزاوية
$$\begin{gathered} 13) \int \left(\sin \left(2x+3\right)+ \cos \left(3x+2\right)\right) dx \\ =-\frac{1}{2} \cos (2x+3) +\frac{1}{3} \sin (3x+2) +C \end{gathered}$$	تكامل اقتراني جيب الزاوية، وجيب تمام الزاوية
$$\begin{gathered} 14) \int \left(\frac{1}{8} x^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} -\frac{ 4}{x}\right) dx =\frac{1}{8}\left(\frac{1}{{\displaystyle \frac{5}{2}}}{x}^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)-4 \ln \left|x\right|+C \\ =\frac{1}{20}{x}^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} -4 \ln \left|x\right|+C \end{gathered}$$	تكامل اقتراني القوة، و $\frac{1}{x}$
$15) \int \frac{1}{\sqrt{x-1}} dx =2 \sqrt{x-1} +C$	تكامل اقتران القوة

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

أجد قيمة كلٍّّ من التكاملات الآتية:

   

$$\begin{gathered} 16) {\int }_0^1\sqrt{1+7x} dx={\int }_0^1{\left(1+7x\right)}^{\frac{1}{2}} dx \\ =\frac{1}{7}\times \frac{2}{3}{\left(1+7x\right)}^{\frac{3}{2}} \overline{)\begin{array}{c}1\\ 0\end{array}} \\ =\frac{2}{21}\left[\sqrt{{\left(1+7\left(1\right)\right)}^3}-\sqrt{{(1+7\left(0\right))}^3}\right] \\ =\frac{2}{21}\left[\sqrt{8^3}-\sqrt{1^3}\right] \\ =\frac{2}{21}\left[\sqrt{512}-1\right] \\ =\frac{2}{21}\sqrt{512} -\frac{2}{21} \end{gathered}$$	استعمال قوانين الأسس النسبية تكامل اقتران القوة تعويض حدود التكامل تبسيط
$$\begin{gathered} 17) {\int }_0^1 e^x\left(4-e^x\right) dx={\int }_0^1\left(4e^x-e^{2x}\right) dx \\ =\left(4 e^x-\frac{1}{2}{e}^{2x}\right)\overline{)\begin{array}{c}1\\ 0\end{array}} \\ =\left(4 e^1-\frac{1}{2}{e}^{2\left(1\right)}\right)-\left(4 e^0-\frac{1}{2}{e}^{2\left(0\right)}\right) \\ =4e-\frac{1}{2}{e}^2-4+\frac{1}{2} \\ =4e - \frac{1}{2}{e}^2-\frac{7}{2} \end{gathered}$$	خاصية توزيع الضرب على  القوس تكامل الاقتران الأسي الطبيعي تعويض حدود التكامل تبسيط
$$\begin{gathered} 18) {\int }_1^3(1+\frac{1}{x}) dx=\left(x+\ln \left|x\right|\right)\overline{)\begin{array}{c}3\\ 1\end{array}} \\ =(3+\ln \left|3\right|)-(1+\ln \left|1\right|) \\ =3+ \ln 3 -1 \\ =2 + \ln 3 \end{gathered}$$	تكامل الثابت،  والاقتران $\frac{1}{x}$ تعويض حدود التكامل  تبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

19) إذا كان ميل المماس لمنحنى العلاقة $y$ هو:$\frac{dy}{dx}= 6 e^{2x} + 2e^{-x}$ ،

      فأجد قاعدة العلاقة $y$، علمًا بأن منحناها يمر بالنقطة $\left(0, 2\right)$.

الحل:

الخطوة الأولى:أجد تكامل المشتقة :

                                 $$\begin{gathered} y=\int \left(6 e^{2x} + 2e^{-x}\right) dx \\ =\frac{6}{2}{e}^{2x} -2e^{-x} +C \\ =3e^{2x} -2e^{-x} +C \end{gathered}$$

الخطوة الثانية:أجد ثابت التكامل$C$ بتعويض النقطة $\left(0, 2\right)$ :

                 $$\begin{gathered} 2=3e^{2\left(0\right)} -2e^{-\left(0\right)} +C \\ 2=3 -2 +C \\ 2-1 =C \\ \to 1 = C \end{gathered}$$

الخطوة الثالثة:أكتب قاعدة العلاقة $y$ :

                 $y=3e^{2x} -2e^{-x} +1$

---

في كل مما يأتي المشتقة الأولى للاقتران$f\left(x\right)$ ؛ ونقطة يمر بها منحنى$y=f\left(x\right)$.

أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران $f\left(x\right)$ :

المعلومات المعطاة	قاعدة الاقتران $f\left(x\right)$
$20) f \mathit{َ}\mathbf{ }(x) = e^{-x} ; (0 , 3 )$	$$\begin{gathered} f\left(x\right)=\int e^{-x} dx \\ =-e^{-x} +C \\ f\left(0\right)=-e^{-\left(0\right)} +C \\ 3 = -1 + C \\ 4 = C \\ f\left(x\right)=-e^{-x} +4 \end{gathered}$$
$21) f \mathit{َ}\mathbf{ }(x) =\frac{3}{x} -4 ; (1 , 0 )$	$$\begin{gathered} f\left(x\right)=\int \left(\frac{3}{x}-4\right)dx \\ =3 \ln \left|x\right|-4x + C \\ f\left(1\right)=3 \ln \left|1\right|-4\left(1\right) + C \\ 0 = -4+C \\ \to C=4 \\ \therefore f\left(x\right)=3 \ln \left|x\right|-4x + 4 \end{gathered}$$
$22) f \mathit{َ}\mathbf{ }(x) =4 e^x -2; (0 , 1 )$	$$\begin{gathered} f\left(x\right)=\int (4e^x-2)dx \\ =4e^x-2x+C \\ f\left(0\right) =4 e^{\left(0\right)} -2\left(0\right)+C \\ 1 = 4 +C \\ 1-4 = C \\ -3=C \\ f\left(x\right)=4e^x-2x-3 \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

23) تلوث: يُعالج التلوث في بحيرة باستعمال مضاد للبكتيريا. إذا كان عدد الخلايا البكتيرية الضارة لكل مليلتر من الماء في البحيرة يتغير بمعدل:     $N \mathit{َ}\mathbf{ }\left(t\right)=-\frac{2000 t }{1+ t^2}$،

                  حيث $N\left(t\right)$  عدد الخلايا البكتيرية لكل مليلتر من الماء بعد t  يومًا من استعمال المضاد،

                 فأجد $N\left(t\right)$، علمًا بأن العدد الابتدائي للخلايا هو 5000 خلية لكل مليلتر.

 

الحل:

 

         $$\begin{gathered} N\left(t\right)=\int -\frac{2000 t }{1+ t^2} dt \\ =-1000\int \frac{2t}{1+t^2} dt \\ =-1000 \ln \left|1+t^2\right|+C \\ N\left(0\right)=-1000 \ln |1+{\left(0\right)}^2|+C \\ 5000=-1000 \ln 1 +C \\ \to 5000 = C \\ \therefore N\left(t\right)=-1000 \ln |1+t^2|+5000 \end{gathered}$$

 

 

---

24)أحدد أوجه الاختلاف بين التكاملين الآتيين من دون إيجاد التكامل:

           $\int \left(3 sin 3 x + 1\right) dx \int \left(3sin(3x+1)\right) dx$

الحل:

الاقتران $(3 sin 3 x + 1)$ يتكون من حدين هما: $3 sin 3x$ وَ $1$،

فلإيجاد التكامل أطبق قاعدة مجموع تكامل الاقترانين: المثلثي والثابت.

 

أما الاقتران $\left(3sin(3x+1)\right)$ فهو يتكون من حد مثلثي واحد فقط.

---

انتهت أسئلة الدرس