تمثيل المُتباينات الخطيّة بمُتغيّرَين بيانيًّا
Graphing Linear Inequalities in Two Variables
فكرةُ الدرسِ : تمثيل مُتباينة خطيَّة بمُتغيّرين بيانيًّا.
أولًا : المُتباينات الخطية بمُتغيرين
المُتباينة الخطيّة بمُتغيرين : هِيَ مُتباينة يمكن كتابتُها على إحدى الصور الآتية :
ax + by < c ax + by ≤ c ax + by > c ax + by ≥ c
حيثُ a , b , c أعدادٌ حقيقيَّةٌ ، و a و b لا تساويان صفرًا معًا، وَحَلُّ المُتباينةِ الخطيَّةِ بِمُتَغيّرين هُو مجموعة جميع الأزواجِ المُرَتَّبَةِ ( x , y )، التي تجعل
المُتباينة صحيحةً عند تعويض إحداثِيّاتها في المُتَبايِنَة.
|
•• أتعلَّم : لكلِّ مُتباينة خطيَّة مُعادلة خطيَّة مُرتبطة بها. فمثلًا ، x + y > 3 هِيَ مُتباينةٌ خطيَّةٌ وَ x + y = 3 هي المُعادلة الخطيَّة المُرتبطة بها. |
مثال 1 :
أُحَدِّد إذا كان كلُّ زوج مُرَتّب ممّا يأتي يمثِّل حلًّ للمُتباينة :
a) (0 , 2)
أُعوّض الزّوج المُرَتّب في المُتباينة :
| المتباينة المعطاة | |
| بتعويض: | |
| الناتج صحيح |
أُلاحظُ عند تعويض الزّوج المُرتب في المُتباينة أنَّ الناتج يكون صحيحًا. إذن، الزَّوج المُرتب ( 2 , 0) هُو أحد الحُلول المُمكنة للمُتباينة.
b) (5 , 1)
أُعوّض الزّوج المُرَتّب في المُتباينة :
| المتباينة المعطاة | |
| بتعويض | |
| الناتج غير صحيح |
أُلاحظ عند تعويض الزّوج المُرتب في المُتباينة أنَّ الناتج لا يكون صحيحًا. إذن، الزَّوج المُرتب ( 1 , 5) ليس أحد الحُلول المُمكنة للمُتباينة.
| •• أتعلَّم : يُستخدم الرَّمز للدَّلالة على عدم تحقُّق المُتباينة. |
c) ( -4 , -1)
أُعوّض الزّوج المُرَتّب في المُتباينة :
| المتباينة المعطاة | |
| بتعويض: | |
| الناتج صحيح |
أُلاحظُ عند تعويض الزّوج المُرتب في المُتباينة أنَّ الناتج يكون صحيحًا. إذن، الزَّوج المُرتب ( 1- , 4-) هُو أحد الحُلول المُمكنة للمُتباينة.
ثانيًا: تمثيل المُتباينات الخطيَّة بمُتغيرين بيانيًّا
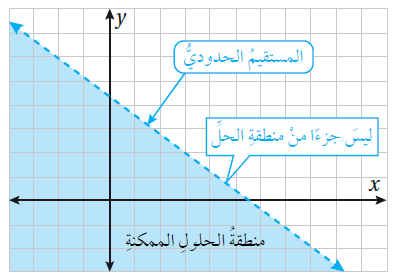
أُلاحظُ من المثال السابق أنَّ مجموعة حَلِّ المُتباينة الخطيَّة بِمُتغيّرين تتكوَّن من العديد من الأزواج المُرَتّبة الَّتي تحقِّقُ المُتباينة، وعند تمثيل المُتباينة الخطيَّة بمُتغيّرين بيانيًّا في المُستوى الإحداثيِّ فإنَّ النقاط الَّتي تُمثِّل جميع حُلولها المُمكنة تُسمى منطقة الحُلول المُمكنة ، وَيُسمى المُستقيم الذي يُقَسِّمُ المُستوى الإحداثيَّ إلى جُزأين، أحدُهما منطقةُ الحُلول المُمكنة، المُستقيم الحُدوديَّ .
•• وقد يكون المُستقيم الحُدوديُّ جُزءًا من منطقة الحُلول المُمكنة إذا تضمَّنَت المُتباينة الرَّمز ≥ أو الرَّمز ≤ ، وعندئذٍ يُرسَمُ المُستقيم الحُدوديُّ مُتَّصِلًا.
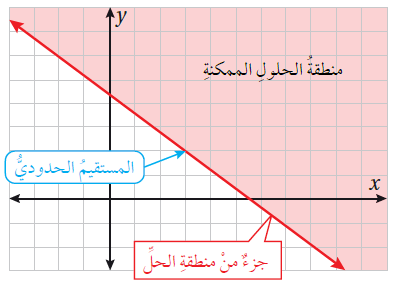
•• وقد لا يكون المُستقيم الحُدوديُّ جُزءًا من منطقة الحُلول المُمكنة إذا تضمَّنَت المُتباينة الرَّمز > أو الرَّمز < ، عندئذٍ يُرسَمُ المُستقيم الحُدوديُّ مُتقطِّعًا.
مفهوم أساسي (تمثيل المُتباينات الخطيّة بمُتغيرين بيانيًّا)
|
لتمثيلِ المُتباينات الخطيَّة بمُتغيرين بيانيًّا، أتَّبع الخُطوات الآتية : الخُطوةُ 1 : أرسُمُ مُنحنى المُعادلةِ المُرافقة للمُتباينة بأنْ أستخدم رمز المُساواة (=) بدلًا من الرَّمز ( ≥ ، ≤ ، > ، < ) ؛ حيثُ تُمثِّل المُعادلة الناتجة المُستقيم الحُدوديَّ. الخطوةُ 2 : أختار نقطةً لا تقعُ على المستقيم الحُدوديِّ، ثمَّ أُعَوِّضُها في المُتباينة الخطيَّة لتحديد ما إذا كانتْ تمثِّل حَلًّ للمُتباينة أمْ لا. الخطوةُ 3 : إذا كانت النقطة تحقِّقُ المُتباينة ؛ أي تنجُمُ عنها نتيجةٌ صحيحةٌ، فَأُظَلِّلُ الجُزء من المُستوى الإحداثيِّ الذي تقع فيه تلك النقطة ، وإذا لم تكن كذلك أُظَلِّل الجُزء الآخر الذي لا تقع فيه تلك النقطة. |
مثال 2 :
أُمَثِّلُ المُتباينة الخطيَّة في المُستوى الإحداثيّ.
الحل :
الخطوة 1 : أُمَثّل المُستقيم الحُدوديّ.
أُمَثّل المُستقيم الحُدوديّ ، وَأُنشئ جدول قِيَم يُبَيّن نقاط تقاطع المُستقيم مع المِحورين.
| x | 0 | 6 |
| y | 2- | 0 |
أُعين النقطتَين ( 2- , 0) وَ ( 0 , 6) في المُستوى الإحداثيِّ، ثمَّ أرسُم مُستقيمًا يَمُرُّ بِهما. وبما أنَّهُ لا توجد مُساواةٌ في رَمز المُتباينة، فَيُرسَم
المستقيم الحدوديُّ مُتَقَطِّعًا، كما في الشَّكل الآتي.
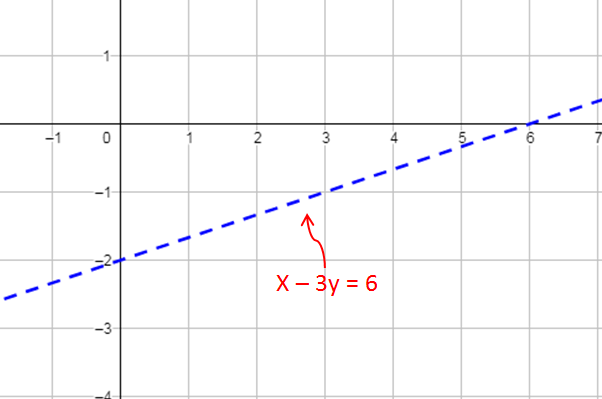
الخطوة 2 : أُحَدّد منطقة الحُلول المُمكنة.
أختار نقطة لا تقعُ على المُستقيم الحُدوديِّ، مثل ( 0 , 0)، ثمّ أتَحَقَّق إذا كان الناتج صحيحًا أم لا عند تعويضها في المُتباينة :
| المُتباينةُ الخطيَّةُ | |
| بتعويضِ: | |
| الناتجُ صحيحٌ |
الخطوةُ 3 : أُظَلِّل منطقة الحُلول المُمكِنة.
بما أنَّ النقطةَ ( 0 , 0) هي إحدى الحُلول المُمكِنة للمُتَبايِنَة، فَأُظَلِّل الجُزء من المُستوى الذي تقع فيه هذه النقطة، كما في الشكل الآتي.
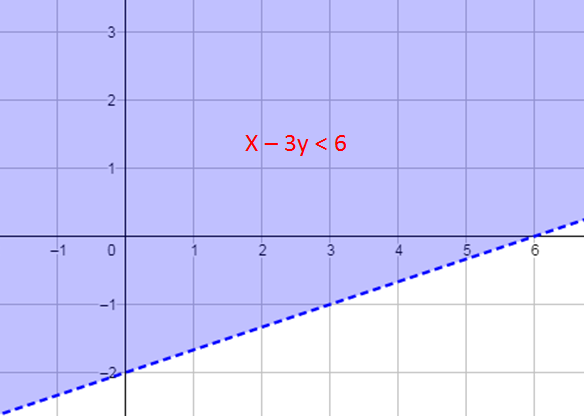
| •• أتعلم : لسهولة إجراء الحسابات ، يُفضّل اختيار النقطةِ(0 , 0) لفحصِ المُتباينة. ولكن ، إذا وقعت على المُستقيم الحُدوديِّ فيجب اختيار نقطة غيرها. |
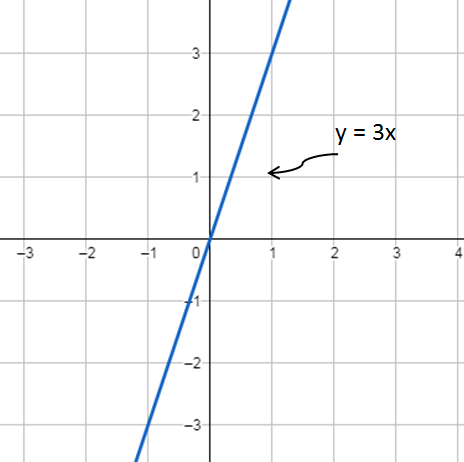
مثال 3 :
أُمَثِّلُ المُتباينةَ الخطيَّةَ في المُستوى الإحداثيِّ.
الحل :
الخطوة 1 : أُمَثّل المُستقيم الحُدوديَّ.
أُمَثّل المُستقيم الحُدوديّ ، وَأُنشئ جدول قِيَم يُبيّن نقاط تقاطع المُستقيم مع المحورين.
| x | 0 | 1 |
| y | 0 | 3 |
أُعين النقطتَين (3 , 1) وَ (0 , 0) في المُستوى الإحداثيِّ، ثمَّ أرسُم مُستقيمًا يَمُرُّ بِهما. وبما أنَّهُ توجد مُساواةٌ في رَمز المُتباينة، فَيُرسَم المستقيم الحدوديُّ متصلًا، كما في الشَّكل الآتي.
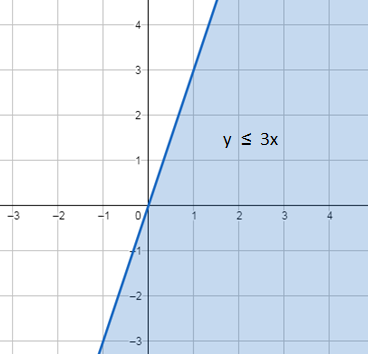
الخطوة 2 : أُحَدّد منطقة الحُلول المُمكنة.
أختار نقطة لا تقعُ على المُستقيم الحُدوديِّ، مثل ( 1 , 0)، ثمّ أتَحَقَّق إذا كان الناتج صحيحًا أم لا عند تعويضها في المُتباينة :
| المُتباينةُ الخطيَّةُ | |
| بتعويضِ: | |
| الناتجُ غير صحيحٌ |
بما أنَّ النقطة ( 1 , 0) ليست إحدى الحُلولِ المُمكِنة للمُتباينة، فأُظلّل الجُزء من المُستوى الذي لا تقع فيه هذه النقطة، كما في الشكل الآتي.
ثالثًا : تمثيل المُتباينات الخطيَّة بمُتغير واحد بيانيًّا
تعلَّمت سابقًا تمثيل المُتباينة الخطيَّة بمُتغير واحد على خطِّ الأعداد، ويمكن أيضًا تمثيلُها في المُستوى الإحداثيِّ.
مثال 4 :
أُمثل كُلًّ من المُتباينات الآتية في المُستوى الإحداثي:
الخطوةُ 1 : أُمَثِّلُ المُستقيمَ الحُدوديَّ.
أُمَثِّلُ المُستقيم الحُدوديّ x = -3 في المُستوى الإحداثيِّ. وَبِما أنَّه توجدُ مُساواةٌ في رَمزِ المُتباينةِ فَيُرسَمُ مُتَّصِلًا.
الخطوةُ 2 : أُحَدِّدُ منطقةَ الحُلولِ المُمكِنةِ.
أختارُ نقطةً لا تقعُ على المُستقيم الحُدوديّ، مثل ( 0 , 0)، ثمَّ أتَحَقّقُ إذا كان الناتج صحيحًا أم لا عند تعويضِها في المُتباينة :
| المُتباينة الخطيّة | |
| بتعويض x = 0 | |
| الناتج صحيح |
الخطوةُ 3 : أُظلل منطقة الحُلول المُمكنة.
بما أنَّ النقطةَ ( 0 , 0) هي إحدى الحُلول المُمكِنة للمُتباينة، فَأُظَلِّل الجُزء من المُستوى الذي تقع فيه هذه النقطة، كما في الشكل الآتي.
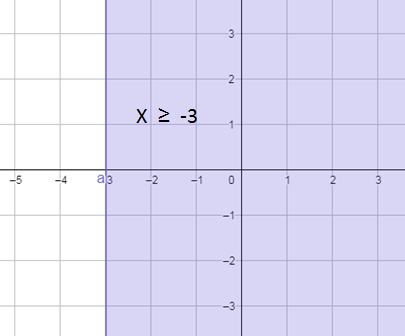
الخطوةُ 1 : أُمَثِّلُ المُستقيم الحُدوديّ.
أُمَثِّلُ المُستقيم الحُدوديّ y = 2 في المُستوى الإحداثيّ. وبما أنّه لا توجدُ مُساواة في رَمز المُتباينة فَيُرسَم متقطعًا.
الخطوةُ 2 : أُحَدِّدُ منطقةَ الحُلول المُمكنة
أختارُ نقطة لا تقع على المُستقيم الحُدوديّ، مثل ( 0 , 0)، ثمَّ أتَحَقّقُ إذا كان الناتج صحيحًا أم لا عند تعويضها في المُتباينة :
| المُتباينة الخطيّة | |
| بتعويض y = 0 | |
| الناتج صحيح |
الخطوةُ 3 : أُظلل منطقة الحُلول المُمكنة.
بما أنَّ النقطةَ ( 0 , 0) هي إحدى الحُلول المُمكِنة للمُتباينة، فَأُظَلِّل الجُزء من المُستوى الذي تقع فيه هذه النقطة، كما في الشكل الآتي.
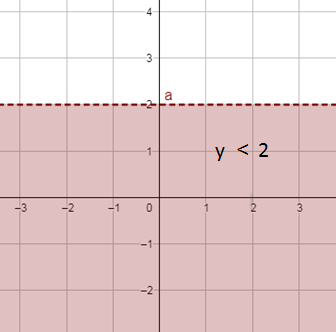
| •• أتعلم : عند تمثيل المُتباينة الخطيّة بمُتغيّر واحد في المُستوى الإحداثيّ، يكون المُستقيم الحُدوديّ إمّا أُفُقيًّا أو عموديًّا. |
•• للمُتباينات استعمالات كثيرة في المواقف العلميَّة والحياتيَّة ؛ إذ تُساعِدُنا على اتِّخاذ القرار الأنسب المُتعلِّقِ بتحديد القِيَم المُمكِنة ضمن شروطٍ مُحددة.
مثال 5 :
يريد همّام شراء نوعين من الفاكهة ، بحيث لا يزيد المبلغ الذي سيدفعه ثمنًا لها عن 5 دنانير ، إذا كان ثمن الفاكهة من النوع الأول 0.75 دينار ، وثمن الفاكهة من النوع الثاني 1.5 دينار ، فأكتب متباينة خطية بمتغيرين تمثل عدد الكيلوغرامات التي يُمكن لهمّام أن يشتريها من كل نوع ، ثمّ أمثلها على المستوى الإحداثي.
الحل :
الخطوةُ 1 : أكتبُ المُتباينةَ.
بالكلماتِ : المبلغ الذي سيدفعه همّام لا يزيد عن 5 دنانير
أختارُ مُتَغَيِّرًا : ليِكَنُ x مُمَثِّلًا لعددِ الكيلو غرامات للفاكهة من النوع الأول ، وَ y ممثلًا لعدد الكيلو غرامات للفاكهة من النوع الثاني
ثمن الفاكهة = عدد الكيلو غرامات مضروبًا في سعر الكيلو الواحد
ثمن الفاكهة من النوع الأول = ، ثمن الفاكهة من النوع الثاني =
أكتبُ المُتباينةَ :
الخطوةُ 2 : أُمَثِّلُ المُتباينةَ بيانيًّا
أُمثل المُستقيم الحُدوديّ في المُستوى الإحداثيّ. وبما أنَّهُ توجد مُساواة في رَمز المُتباينة فَيُرسَمُ المُستقيم الحدوديّ مُتَّصلًا.
أختار نقطة لا تقع على المُستقيم الحُدوديّ، مثل ( 0 , 0)، ثمّ أتحقق إذا كان الناتجُ صحيحًا أم لا عند تعويضِها في المُتباينة :
| المُتباينة الخطيّة | |
| بتعويض: | |
| الناتج صحيح |
بِما أنَّ النقطة ( 0 , 0) هي إحدى الحلولِ المُمكِنَةِ للمُتباينة ، وبما أنَّ قِيَم x وَ y يجب أن تكون موجبة ؛ لأنَّها تمثِّل الوزن ، فَأُظَلِّل الجُزء من المُستوى الذي يقع في الرُّبع الأول، كما في الشكل المُجاور.
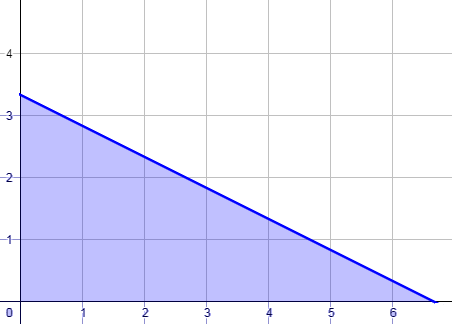
أُلاحظ أيضًا أنّ أيّ نقطة يقع إحداثيُّها على المُستقيم الحُدوديّ، أو ضمن المنطقة المُظَلَّلَة، فإنّها تُعَدُّ حَلًا. فمثلًا ، النقطة (1 , 4) تُمثّل حلًا للمُتباينة، وَ ( 2 , 2) تُمثل أيضًا حلًا لها.