رياضيات فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 36

أُحَدّد إذا كان كلُّ زوج مُرتّب ممّا يأتي يمثِّل حلّ للمُتباينة $-2x + 3y \ge 3$  :

a) (4, 1)                                       b) (-1, 2)                                               c) (0, 1)

الحل : 

a) (4, 1) 

 

أعوض $(4 , 1)$ في المتباينة : 

$$\begin{gathered} -2x + 3y \ge 3 \\ -2\left(4\right) + 3\left(1\right) \stackrel{؟}{\ge } 3 \\ -5 \ngeqq 3 ✘ \end{gathered}$$   

الزوج المرتب (1, 4) ليس حلًا للمتباينة . 

---

 b) (-1, 2) 

أعوض $(-1 , 2)$ في المتباينة : 

$$\begin{gathered} -2x + 3y \ge 3 \\ -2(-1) + 3\left(2\right) \stackrel{؟}{\ge } 3 \\ 8 \ge 3 ✔ \end{gathered}$$

الزوج المرتب (2 , 1-) يُعد حلًا للمتباينة . 

---

   c) (0, 1)

أعوض $(0 , 1)$ في المتباينة : 

$$\begin{gathered} -2x + 3y \ge 3 \\ -2\left(0\right) + 3\left(1\right) \stackrel{؟}{\ge } 3 \\ 3 \ge 3 ✔ \end{gathered}$$

الزوج المرتب (3 , 0) يُعد حلًا للمتباينة . 

---

أتحقق من فهمي صفحة 39

أُمَثّل المُتباينة الخطيّة x + 2y > 2 - في المُستوى الإحداثيّ.

الحل : 

---

 

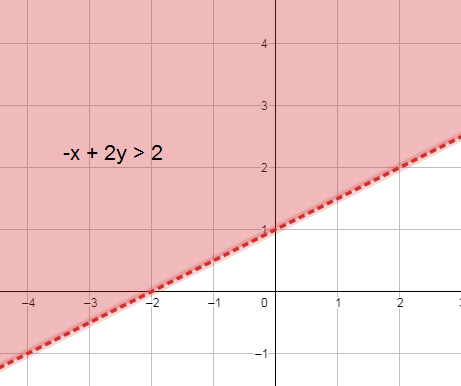
أتحقق من فهمي صفحة 40

أُمثّل المُتباينة الخطيّة y - 3x ≤ 0 في المُستوى الإحداثيّ.

الحل : 

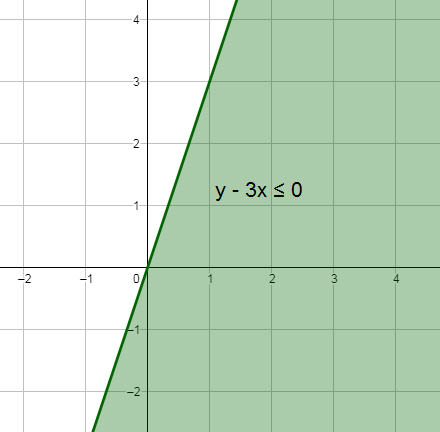
أتحقق من فهمي صفحة 42

أُمثل كُلًّ من المُتباينات الآتية في المُستوى الإحداثيّ:

a) x ≤ 4                                    b) y > -5                                      c) y ≥ 0

الحل : 

a) x ≤ 4

---

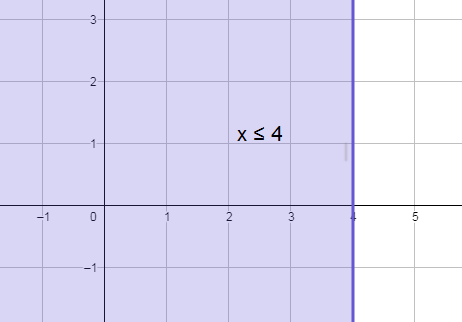
 b) y > -5

---

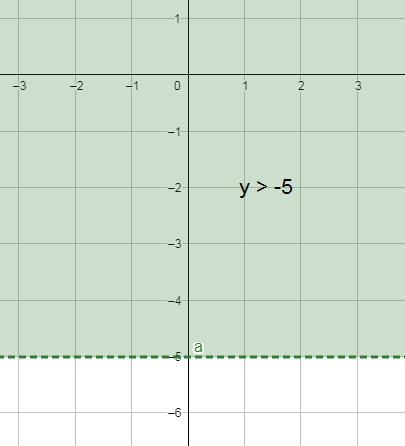
c) y ≥ 0

---

 

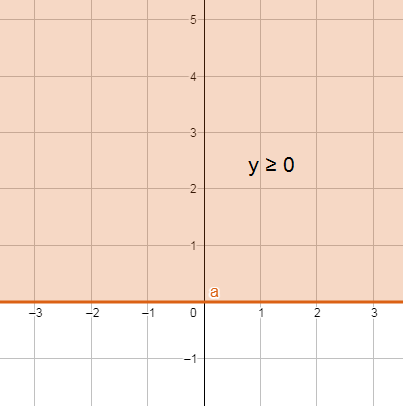
أتحقق من فهمي صفحة 44

نِجارة : إذا عَلِمت أنَّ نجارًا يريد شراء نوعَين من الخشب، لا يزيدُ ثمنُهُما الكليُّ على JD 72  ، وَوُجِد أنَّ ثمن المتر الطوليِّ من النَّوع الأوَّل JD 4 ، ومِن

النَّوع الثاني JD 6 ، فأكتبُ مُتباينة خطيَّة بِمُتغيرين تمثِّل كميَّة الخشب التي يمكنُ للنَّجار شِراؤها من كلِّ نوع، ثمَّ أُمَثِّلُها في المُستوى الإحداثيِّ.

الحل : 

الخطوةُ 1 : أكتبُ المُتباينةَ.

بالكلماتِ : المبلغ الذي سيدفعه النجار  لا يزيد عن 72 دبنار

أختارُ مُتَغَيِّرًا : ليِكَنُ x مُمَثِّلًا لعددِ الأمتار الطولية من النوع الأول ، وَ y ممثلًا لعدد الأمتار الطولية من النوع الثاني  

ثمن الأمتار = عدد الأمتار مضروبًا في سعر المتر الطولي الواحد 

$\Leftarrow$ ثمن الأمتار  من النوع الأول  = $4 x$ ، ثمن الأمتار  من النوع الثاني  = $6 y$

أكتبُ المُتباينةَ : $4x + 6y \le 72$

أمثل المتباينة  : 

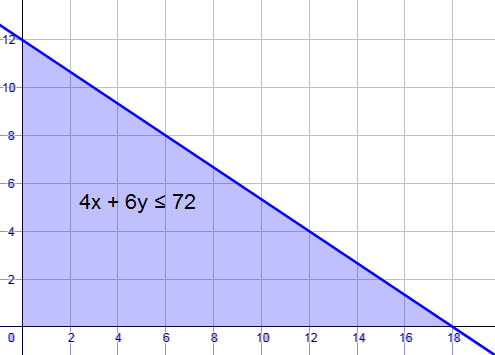
بما أنَّ قِيَم x وَ y يجب أن تكون موجبة ؛ لأنَّها تمثِّل طول ، فَأُظَلِّل الجُزء من المُستوى الذي يقع في الرُّبع الأول فقط . 

وأُلاحظ أنّ أيّ نقطة يقع إحداثيُّها على المُستقيم الحُدوديّ، أو ضمن المنطقة المُظَلَّلَة، فإنّها تُعَدُّ حَلًا. فمثلًا ، النقطة (4 , 12) تُمثّل حلًا للمُتباينة، وَ (6 ,  8) تُمثل أيضًا حلًا لها.

---

 

 

أسئلة أتدرب وأحل المسائل

أُحدِّد إذا كان كلُّ زوج مُرتب ممّا يأتي يمثّل حلًا للمُتباينة : $x + 3y < 6$

1) (0, 1)                                                   2) (-2, 4)                                       3) (8, -1)

الحل : 

1) (0, 1)   

أعوض (1, 0) في المتباينة 

$$\begin{gathered} x + 3y < 6 \\ 0 + 3\left(1\right) = 3 < 6 ✔ \end{gathered}$$

---

2) (-2, 4)

أعوض (4,  2-) في المتباينة 

$$\begin{gathered} x + 3y < 6 \\ -2 + 3\left(4\right) = 10 < 6 ✘ \end{gathered}$$

---

3) (8, -1)

أعوض (1-,  8) في المتباينة 

$$\begin{gathered} x + 3y < 6 \\ 8 + 3(-1) = 5 < 6 ✔ \end{gathered}$$

---

 

أُحدِّد إذا كان كلُّ زوج مُرَتّب ممّا يأتي يمثّل حلًا للمُتباينة : $-3x + 4y \ge 12$

4) (-5, 3)                                                 5) (0, 2)                                         6) (3, 7)

الحل : 

4) (-5, 3)

أعوض (3, 5-) في المتباينة 

$$\begin{gathered} -3x + 4y \ge 12 \\ -3(-5) + 4\left(3\right) = 27 \ge 12 ✔ \end{gathered}$$

---

5) (0, 2)

أعوض (2, 0) في المتباينة 

$$\begin{gathered} -3x + 4y \ge 12 \\ -3\left(0\right) + 4\left(2\right) = 8 \ge 12 ✘ \end{gathered}$$

---

6) (3, 7)

 أعوض (7, 3) في المتباينة

$$\begin{gathered} -3x + 4y \ge 12 \\ -3\left(3\right) + 4\left(7\right) =19 \ge 12 ✔ \end{gathered}$$

---

أُمثّل كُلًا من المُتباينات الآتية في المُستوى الإحداثيّ :

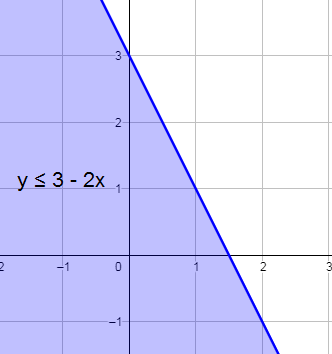
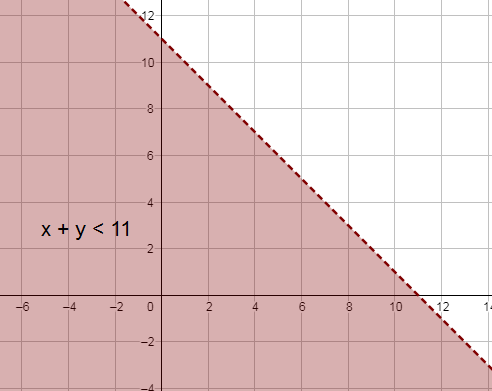
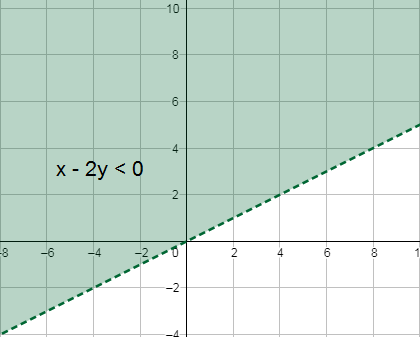
7) y ≤ 3 - 2x                                    8) x + y < 11                                                9) x - 2y < 0                                       10) 4y - 8 ≥ 0

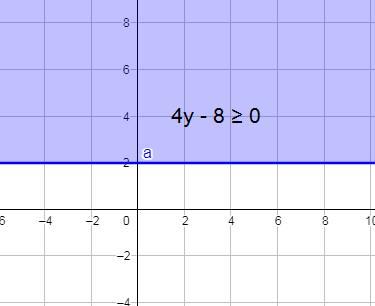
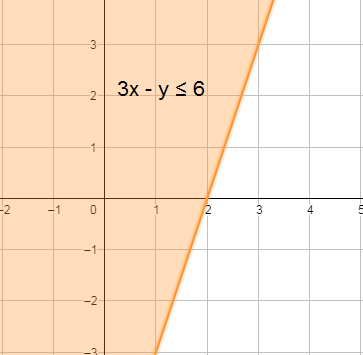
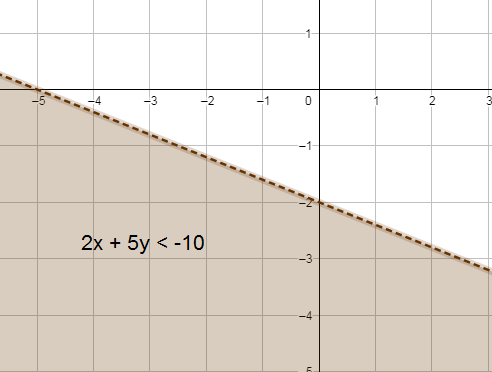
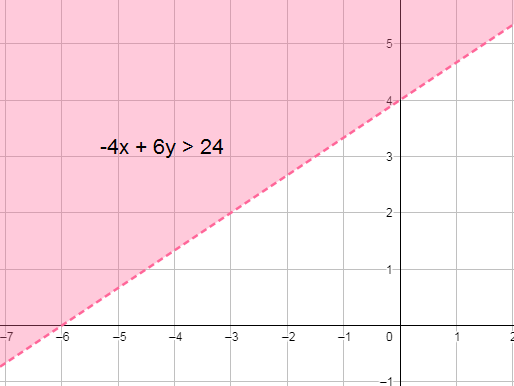
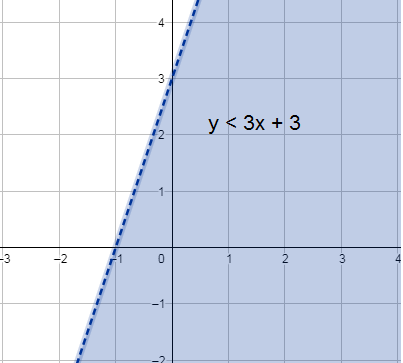
11) 3x - y ≤ 6                                 12) 2x + 5y < -10                                         13) -4x + 6y > 24                                14) y < 3x + 3

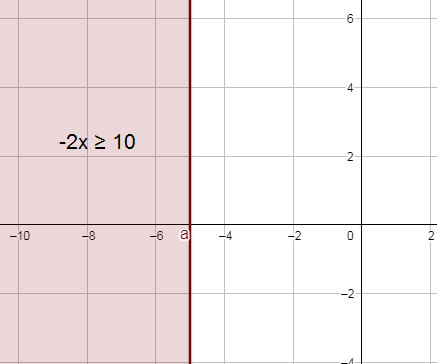
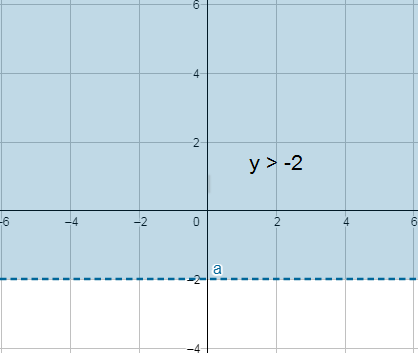
15) -2x ≥ 10                                  16) x < 6                                                      17) y > -2                                             18) $\frac{x}{2}+\frac{y}{2}<1$ 

الحل : 

7) y ≤ 3 - 2x 

---

8) x + y < 11

---

9) x - 2y < 0

---

10) 4y - 8 ≥ 0

---

11) 3x - y ≤ 6

---

12) 2x + 5y < -10

---

13) -4x + 6y > 24

---

14) y < 3x + 3

---

15) -2x ≥ 10

 

---

16) x < 6

---

17) y > -2

---

 18) $\frac{x}{2}+\frac{y}{2}<1$

---

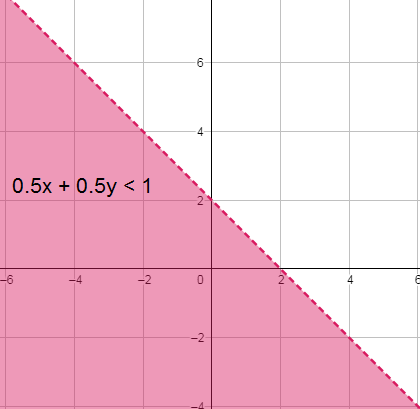
19) حقائب: يصنع جمالٌ حقائب نسائية كبيرة وصغيرة لبيعها في معرض الحرف اليدويّة. إذا كان يحتاج إلى 3 أيام لصنع الحقيبة الصغيرة، و 5 أيام

لصنع الحقيبة الكبيرة، فأكتبُ مُتباينة خطيّة بمُتغيرين تمثّل عدد الحقائب التي يمكن له صنعها من كلِّ نوع في 30 يومًا حدًّا أقصى قبل يوم افتتاح

المعرض، ثمّ أُمثلها في المُستوى الإحداثيِّ.

الحل : 

أفرض عدد الحقائب الصغيرة = x ، وعدد الحقائب الكبيرة = y 

المتباينة : $3x + 5y \le 30$

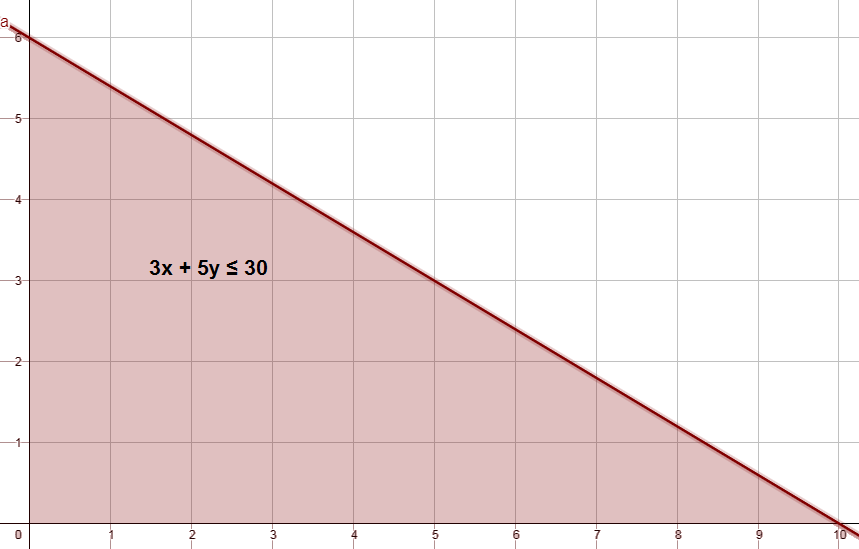
منطقة الحلول الممكنة هي المنطقة المظللة في الربع الأول لأن عدد الحقائب لا يكون سالبًا ، ويؤخذ من منطقة الحل الأعداد الصحيحة لأن عدد الحقائب لا يكون إلا عددًا صحيحًا. 

المتباينة : $1.5 x + y \le 6$

 

---

20) تسوُّق : تريدُ ساميةُ شراء العِنب وَالتُّفّاح، بحيث لا يزيد المبلغ الذي تدفَعهُ ثمنًا لكلا النَّوعين على JD 6 . إذا كان ثمن الكيلوغرام الواحد من

العنب JD 1.5 ، وثمن الكيلوغرام الواحد من التفاح JD 1 ، فأكتب مُتباينة خطيّة بمُتغيرين تمثِّل عدد الكيلوغرامات التي يمكن لسامية أنْ تشتَريها

من كلِّ نوع، ثمَّ أُمَثلُها في المُستوى الإحداثيِّ.

الحل : 

أفرض عدد الكيلو غرامات من العنب = x ، وعدد الكيلو غرامات من التفاح = y 

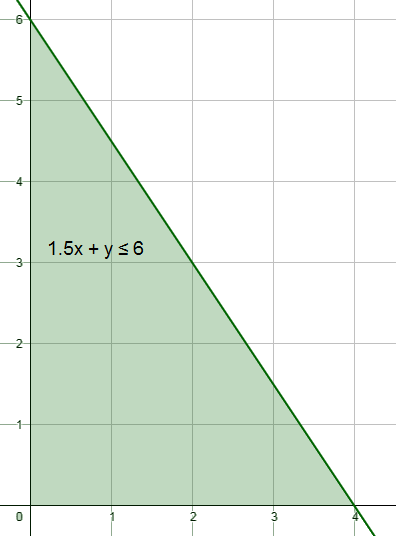
منطقة الحلول الممكنة هي المنطقة المظللة في الربع الأول لأن عدد الكيلو غرامات لا يكون سالبًا.

---

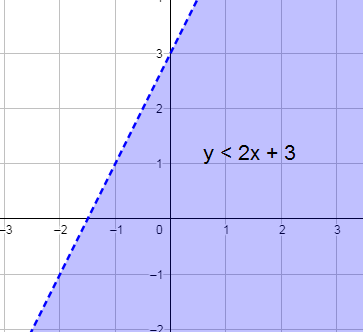
21) أكتشفُ الخطأَ: مثّل رامي المُتباينة y < 2x + 3 ، كما هُو مُبين في الشكل المُجاور. أكتشف الخطأ الذي وقع فيه رامي، وأُصححهُ.

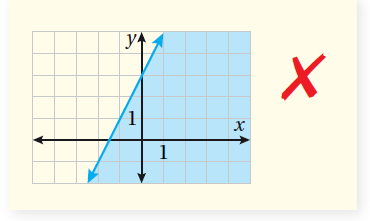
الحل : 

المتباينة لا تحتوي على رمز المساواة ؛ لذا يجب أن يُرسم المستقبم الحدودي متقطعًا. 

---

22) مسألةٌ مفتوحةٌ : أكتبُ مُتباينة خطيّة بمُتغيرين، بحيث تمثل النقطتين ( 3 , 1-) وَ ( 6 , 1) حَلًّ لها، في حين لا تمثِّل النقطة ( 0 , 4) حلًا.

الحل : 

حل مقترح :  $y - x > 1$

 

---

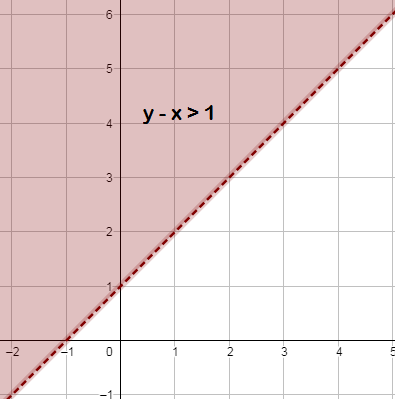
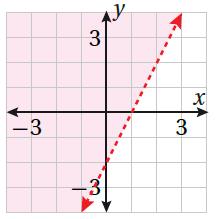
23) تبرير : أكتب المُتباينة الخطيّة المُعطى تمثيلُها البيانيّ في الشكل المُجاور ، مُبررًا إجابتي.

الحل : 

أجد معادلة الخط المستقيم  : 

النقطتين : (2 ، 2) ، (0 ، 1) تقعان على الخط المستقيم 

$m = \frac{y_2 - y_1}{x_2 - x_1} =\frac{2-0}{2-1} = 2$

معادلة المستقيم  : 

$$\begin{gathered} y - y_1 = m (x - x_1) \\ y - 0 = 2 (x - 1) \\ y = 2x - 2 \end{gathered}$$
 
أختبر نقطة تقع في منطقة الحل ، ولتكن (0 ، 0) وأعوضها في معادلة الخط المستقيم :

$$\begin{gathered} y = 2x - 2 \\ 0 \stackrel{?}{=} 2\left(0\right) - 2 \\ 0 > -2 \end{gathered}$$

الطرف الأيسر من المعادلة أكبر من الطرف الأيمن ،  

إذن ، المتباينة  :  $y > 2x - 2$   ، ولأن المستقيم الحدودي مرسوم متقطعًا ، فلا توضع إشارة المساواة في المتباينة .

---

 أسئلة كتاب التمارين 

أُمَثِّلُ كلًّ مِنَ المُتبايناتِ الآتيةِ في المُستوى الإحداثيِّ :  

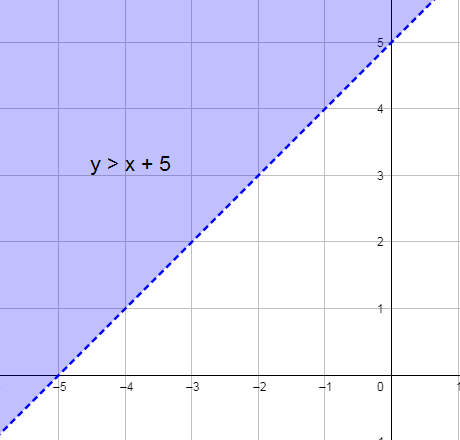
1)  y > x + 5                                 2)  y ≤ - 0.5x +1                                  3)  y  ≥  - x - 5

4) y < 4                                       5) x > 3                                               6) x ≤ -1

7) 3y > 6 + 2x                             8) y ≥ -x + 1                                         9) x + 2y < 4

 الحل : 

1)  y > x + 5 

---

 2)  y ≤ - 0.5x +1 

---

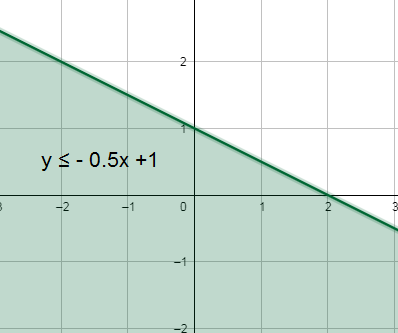
 3)  y  ≥  - x - 5

---

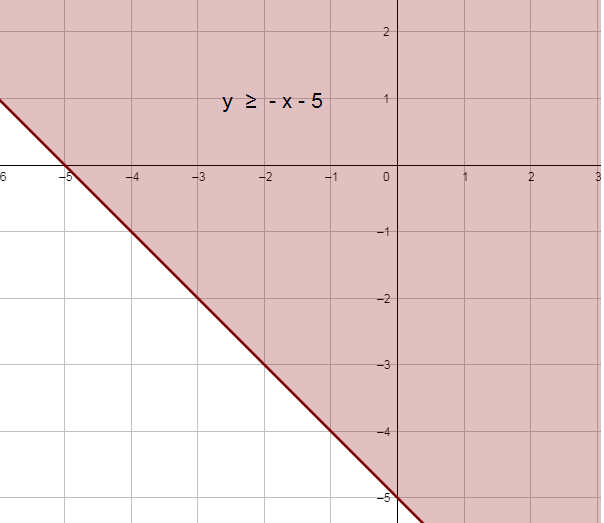
4) y < 4 

---

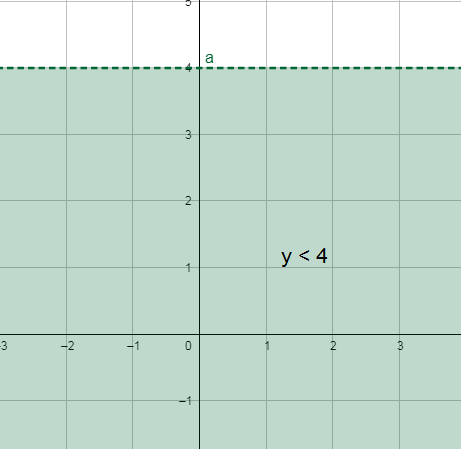
 5) x > 3 

---

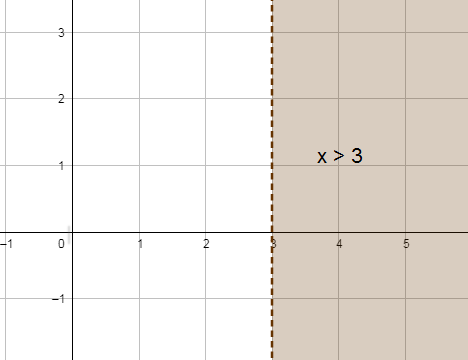
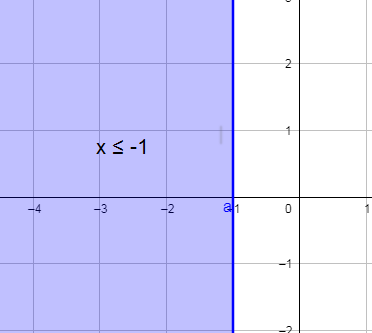
6) x ≤ -1

---

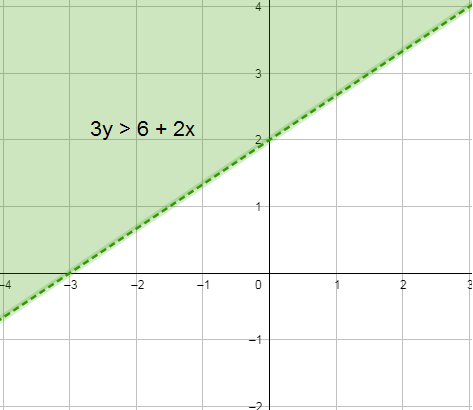
7) 3y > 6 + 2x 

---

8) y ≥ -x + 1 

---

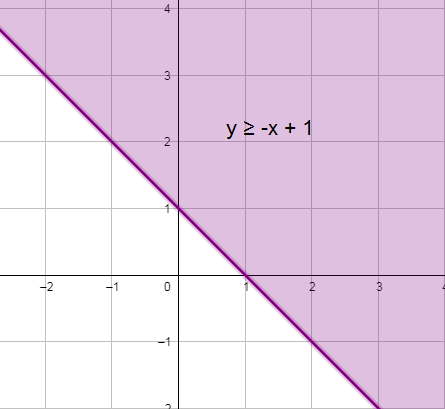
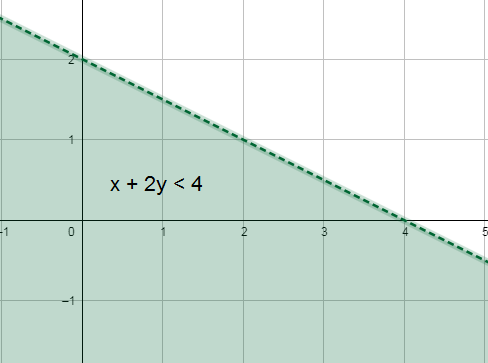
  9) x + 2y < 4

---

أُحدد إذا كان الزوج المُرتب يمثل حلًّ للمُتباينة أم لا في كلٍّ مما يأتي :

10)  x + y < 7 , (2, 11)                                    11)  x < 3y , (-9, 2)                              12) -4x - 8y ≤ 15 , (-6, 3)

13) -x - 6y > 12 , (-1, 3)                                 14) 5x + 7y ≤ 10 , (-1, 2)                       15) 8x + y > -6 , (0, -8)

 الحل : 

10)  x + y < 7 , (2, 11) 

أعوض (11, 2) في المتباينة  

 $$\begin{gathered} x + y < 7 \\ 2 + 11 = 13 < 7 ✘ \end{gathered}$$

---

 11)  x < 3y , (-9, 2)  

أعوض (2 , 9-) في المتباينة

$$\begin{gathered} x < 3y \\ -9 < 3\left(2\right) \\ -9 < 6 ✔ \end{gathered}$$

---

 12) -4x - 8y ≤ 15 , (-6, 3)

أعوض (3 , 6-) في المتباينة

$$\begin{gathered} -4x - 8y \le 15 \\ -4(-6) - 8\left(3\right) = 0 \le 15 ✔ \end{gathered}$$

---

13) -x - 6y > 12 , (-1, 3)

 أعوض (3 , 1-) في المتباينة  

$$\begin{gathered} -x - 6y > 12 \\ -(-1) - 6\left(3\right) = -17 > 12 ✘ \end{gathered}$$

---

 14) 5x + 7y ≤ 10 , (-1, 2)  

 أعوض (2 , 1-) في المتباينة  

$$\begin{gathered} 5x + 7y \le 10 \\ 5(-1) + 7\left(2\right) = 9 \le 10 ✔ \end{gathered}$$

---

15) 8x + y > -6 , (0, -8)

 أعوض (8- , 0) في المتباينة  

$$\begin{gathered} 8x + y > -6 \\ 8\left(0\right) + (-8) = -8 > -6 ✘ \end{gathered}$$

---

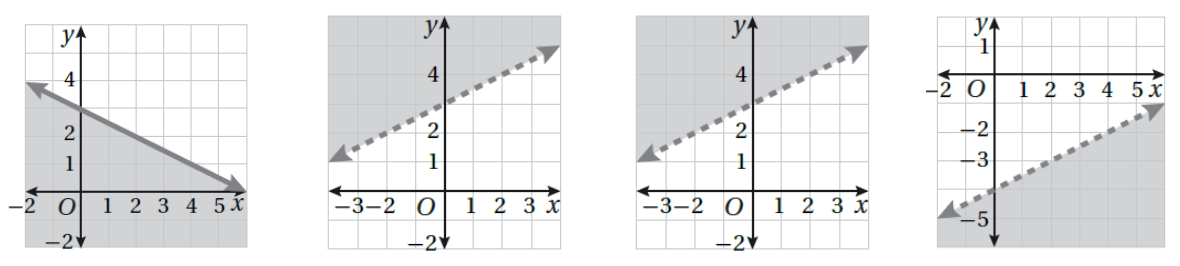
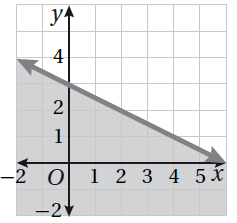
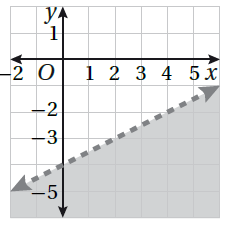
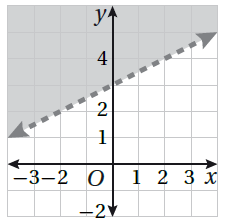
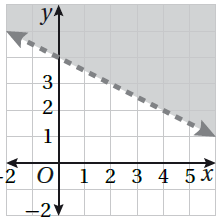
أَصِلُ المُتباينةَ بتمثيلِها البيانيِّ في كلٍّ ممّا يأتي :

16)  2y + x  ≤  6                   17) 0.5 x - y > 4                      18) y > 3 + 0.5x                       19) 4y + 2x > 16

                                                   

الحل : 

16)  2y + x  ≤  6	17) 0.5 x - y > 4	18) y > 3 + 0.5x	19) 4y + 2x > 16

 

 

  

 

 

 

 

---

20 ) يبيع متجر على شبكة الإنترنت كاميرات رقميّة وهواتف محمولة. إذا كان المتجر يقدّم خصمًا مقدارُه JD 5 عن كلّ كاميرا يبيعُها، و JD 10 عن كلِّ هاتف يبيعهُ، وكان يرغب في تقديم خصم مقدارُه JD 30 على الأكثر على مبيعاته من الكاميرات والهواتف، فإذا باعَ x من الكاميرات،و y من الهواتف، أكتبُ مُتباينة خطيّة بمُتغيرين تمثِّلُ عدد الكاميرات والهواتف التي يجب عليه بيعُها لتحقيق هدفه، ثمّ أُمثلها في المُستوى الإحداثيّ المجاور.

الحل : 

المتباينة  : $5x + 10y \le 30$

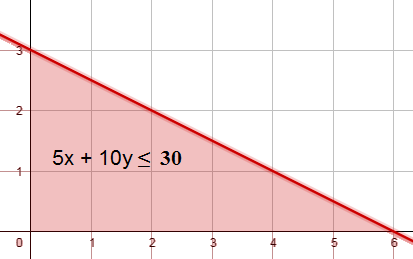
منطقة الحلول الممكنة تقع في الربع الأول من المستوى الإحداثي لأن أعداد الكمرات والهواتف لا يكون سالبًا ، ويُؤخذ من منطقة الحل الأعداد الصحيحة فقط لأن أعداد الكمرات والهواتف لا يكون إلا عددًا صحيحًا . 

---