تستخدم الاقترانات المثلثية في تمثيل مواقف حياتية مرتبطة بالحركة الدورية،
مثل: موجات الصوت، وضغط الدم في جسم الإنسان، وارتفاع مقعد في دولاب دوار،
وتغير عدد ساعات النهار خلال عام، وغير ذلك.
ولكن، هل يمكن رسم منحنى اقتران يبين كيف تبدو الحركة الدورية التي تمثلها هذه الاقترانات؟
تعلمت سابقا كيفية تمثيل اقترانات خطية وتربيعية في المستوى الإحداثي
وذلك بإنشاء جدول قيم للمتغيرين ، وتمثيل كل زوج بنقطة في المستوى،
ثم رسم المنحنى الذي يصل هذه النقاط ببعضها.
وفي هذا السياق، ويمكن اتباع الطريقة نفسها لتمثيل الاقترانات المثلثية
مثال
ارسم منحنى كل من الاقترانين الآتيين ثم أصفه، علما بأن :
الخطوة 1: أكون جدولا أكتب فيه زوايا شائعة، نسبها المثلثية معروفة،
مثل: الزوايا الربعية، والزوايا التي زاويتها المرجعية
الخطوة 2: أجد قيمة لكل زاوية x، ثم اكتبها في الجدول:

الخطوة 3: أعين الأزواج المرتبة: في المستوى الإحداثي
الخطوة 4: أصل بمنحنى أملس بين النقاط، فينتج رسم كما في الشكل المجاور :
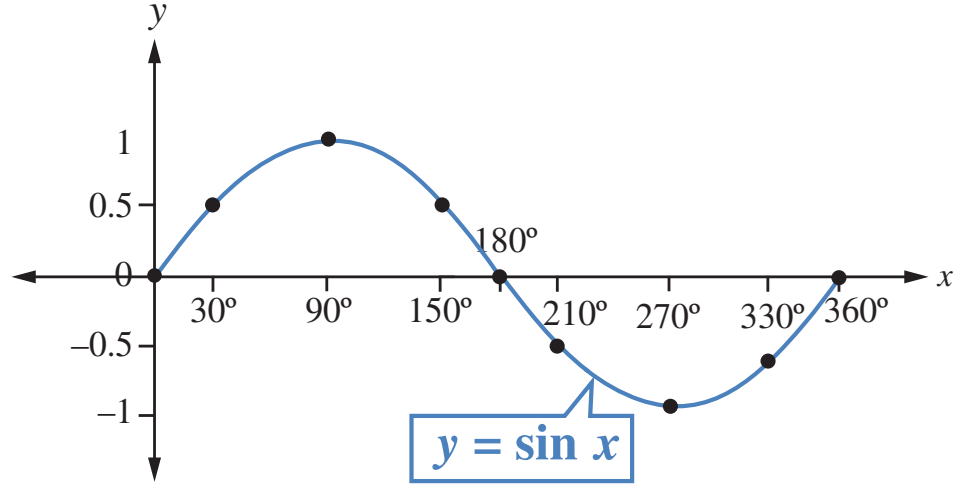
من التمثيل البياني لاقتران ، ألاحظ أن:
-
أكبر قيمة للاقتران هي 1، وأصغر قيمة له هي
-
يكون موجبا إذا كانت ، وسالبا إذا كانت
الخطوة 1: أكون جدولا أكتب فيه زوايا شائعة
الخطوة 2: أجد قيمة لكل زاوية x، ثم اكتبها في الجدول:

الخطوة 3: أعين الأزواج المرتبة: في المستوى الإحداثي،
الخطوة 4: أصل بمنحنى أملس بين النقاط، فينتج رسم كما في الشكل المجاور :
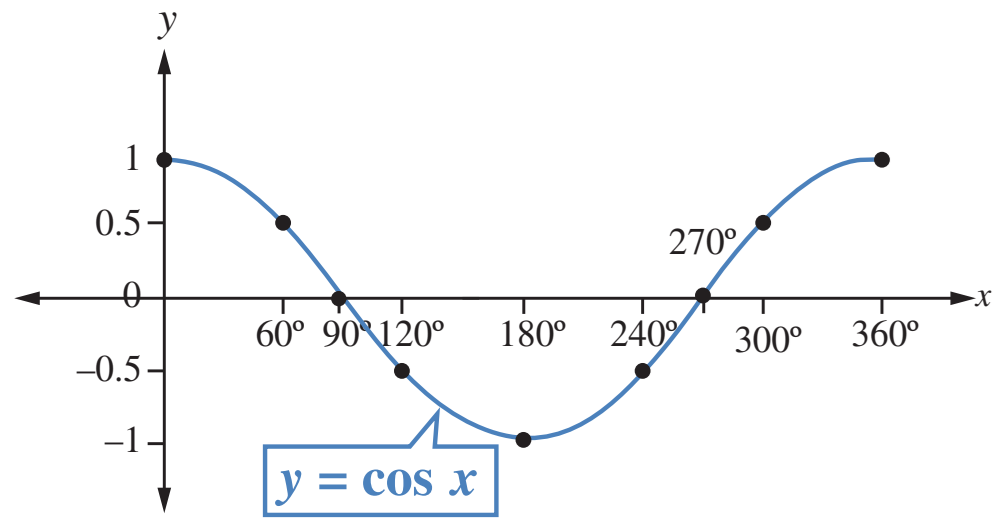
من التمثيل البياني لاقتران ، ألاحظ أن:
-
أكبر قيمة للاقتران هي ، وأصغر قيمة له هي
-
يكون موجبا إذا كانت وسالبا إذا كانت
تعرفت أنه توجد زوايا أكبر من . فإذا دار ضلع انتهاء الزاوية (في الوضع القياسي)
أكثر من دورة واحدة عكس اتجاه عقارب الساعة، فإنه يكون زوايا أكبر من ،
وإذا دار مع اتجاه عقارب الساعة، فإنه يكون زوايا قياسها سالب؛
ولهذا، فقد يكون قياس الزاوية أي عدد حقيقي،
علما بأنه يمكن تمثيل الاقترانات المثلثية للأعداد الحقيقية جميعها،
وليس فقط للزوايا الواقعة بين ، ألاحظ منحنى اقتران الجيب الآتي
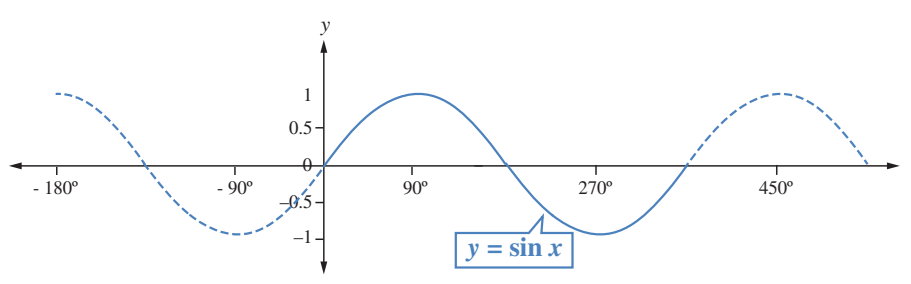
ولأن، سأرسم منحنى الاقتران ، ملاحظا الفرق بينه وبين منحنيي الاقترانين ،و
مثال
ارسم منحنى الاقتران ، ثم أصفه علما بأن
الخطوة 1: أكون جدولا، ثم اكتب فيه زوايا شائعة
الخطوة 2: أجد قيمة لكل زاوية x، ثم اكتبها في الجدول:
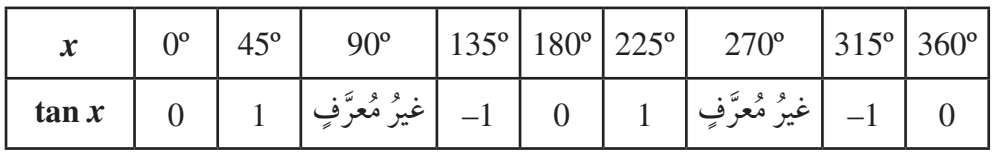
الخطوة 3: أعين النقاط في المستوى الإحداثي، ملاحظا صعوبة التوصيل بين النقاط بمنحنى واحد،
لأن قيمة غير معرفة للزاويتين ؛ لذا أصل النقاط قبل الزاوية ببعضعا،
والنقاط بين الزاويتين ببعضها، والنقاط بعد الزاوية ببعضها،
فينتج رسم كما في الشكل الآتي:
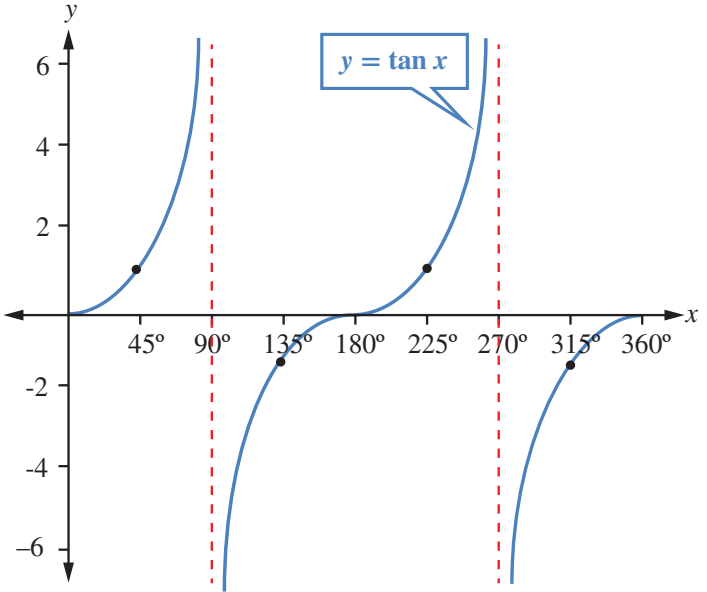
يبين الشكل أن منحنى غير متصل؛ فهو مكون من عدة قطع،
وإن الظل موجب بين الزاويتين ، وبين الزاويتين ،
وأنه يكون سالبا بين الزاويتين ، وبين الزاويتين