رياضيات أدبي فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 79

يُبيِّن الجدول الآتي نتائج مسحٍ شمل 200 أُسرة لمعرفة عدد حيواناتهم الأليفة:

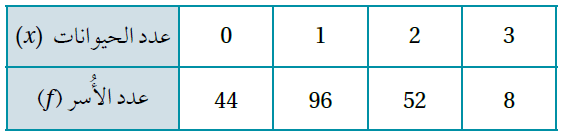
بافتراض أنَّ المتغير العشوائي X يُمثِّل عدد الحيوانات الأليفة، أجد E(x).

الحل : 

أقسم كل تكرار على مجموع التكرارات، ثم أُنشِئ جدولًا للتوزيع الاحتمالي:

3	2	1	0	(x)
0.04	0.26	0.48	0.22	P(x)

 

 

أجد التوقُّع للمتغير العشوائي x.

صيغة التوقُّع للمتغير العشوائي x	$E\left(x\right) = \sum _{}x . P\left(x\right)$
مجاميع حاصل الضرب	$= 0\times 0.22 + 1\times 0.48 + 2\times 0.26 + 3\times 0.04$
بالتبسيط	$\mathbf{=}\mathbf{ }\mathbf{1}\mathbf{.}\mathbf{12}$

 

 

 

 

---

 

أتحقق من فهمي صفحة 81

إذا كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي : 

وكان التوقُّع E(x) = 2.5 ، فأجد قيمة كلٍّ من : ( P(x = 2 و ( P(x = 1.

الحل : 

صيغة التوقُّع للمتغير العشوائي x	$E\left(x\right) = \sum _{}x . P\left(x\right)$
لأنَّ التوقُّع هو 2.5	$= 0\times 0.1 + 1\times a + 2 \times b + 3 \times 0.2 + 4 \times 0.3 = 2.5$
بتجميع الحدود المتشابهة	$= a +2b+1.8 = 2.5$
بالتبسيط	$= a +2b= 0.7 .... \left(1\right)$
مجموع الاحتمالات هو  1	$0.1 + a + b +0.2 + 0.3 = 1$
بتجميع الحدود المتشابهة	$a + b + 0.6 = 1$
بالتبسيط	$a + b = 0.4 ..... \left(2\right)$
بطرح المعادلة (2) من المعادلة (1)	$\mathit{b}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{3}$
أجد a بتعويض قيمة b في المعادلة (2)	$a + 0.3 = 0.4 \Rightarrow \mathbf{ }\mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{1}\mathbf{ }\mathbf{ }$

 

 

 

 

 

 

 

 

 

 

 

إذن  : $P(x = 1) = 0.1 , P(x= 2) = 0.3$

---

 

أتحقق من فهمي صفحة 82

إذا كان للمتغير العشوائي X التوزيع الاحتمالي الآتي :

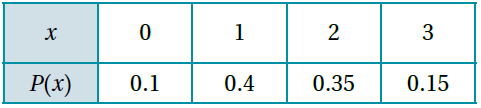
فأجد التوقُّع E(x) ، والتباين ${\sigma }^2$

الحل : 

التوقع E(x)

صيغة التوقُّع للمتغير العشوائي x	$E\left(x\right) = \sum _{}x . P\left(x\right)$
مجاميع حاصل الضرب	$= 0\times 0.1 + 1\times 0.4 + 2\times 0.35 + 3\times 0.15$
بالتبسيط	$\mathbf{=}\mathbf{ }\mathbf{1}\mathbf{.}\mathbf{55}$

 

 

 

 

التباين ${\sigma }^2$

صيغة التباين للمتغير العشوائي x	${\sigma }^2 = (\sum _{}{x}^2. P(x\left)\right) - (E{\left(x\right))}^2$
بالتعويض	$= (0^2\times 0.1 + 1^2\times 0.4 + 2^2\times 0.35 + 3^2\times 0.15) - {(1.55)}^2$
بالتبسيط	$= 3.15 - 2.4025 \mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{7475}$

 

 

 

 

 

---

 

 

أسئلة أتدرب وأحل المسائل

1)  يُبيِّن الجدول الآتي نتائج مسحٍ شمل 50 طالبًا من إحدى المدارس لمعرفة عدد ساعات الدراسة في يوم الإجازة:

بافتراض أنَّ المتغير العشوائي X يُمثِّل عدد الساعات، أجد  E(x).

الحل : 

أقسم كل تكرار على مجموع التكرارات، ثم أُنشِئ جدولًا للتوزيع الاحتمالي:

5	4	3	2	1	(x)
0.12	0.16	0.4	0.24	0.08	P(x)

 

 

 

$$\begin{gathered} E\left(x\right) = \sum _{}x . P\left(x\right) \\ = 1\times 0.08 + 2 \times 0.24 + 3\times 0.4 + 4 \times 0.16 + 5 \times 0.12 \\ = 0.08 + 0.48 + 1.2 + 0.64 + 0.6 \\ \mathbf{=}\mathbf{ }\mathbf{3} \end{gathered}$$

---

 

2) إذا كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي :

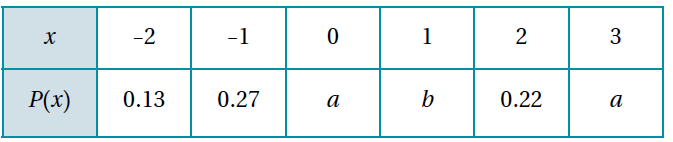
وكان التوقُّع E(x) = 0.39 ، فأجد قيمة كلٍّ من: ( P(x = 1  و ( P(x = 0

الحل : 

صيغة التوقُّع للمتغير العشوائي x	$E\left(x\right) = \sum _{}x . P\left(x\right)$
لأنَّ التوقُّع هو 0.39	$= -2\times 0.13 + -1\times 0.27 + 0 \times a + 1 \times b + 2 \times 0.22 + 3 \times a = 0.39$
بجمع الحدود المتشابهة	$= 3a +b - 0.09 = 0.39$
بالتبسيط	$= 3a +b = 0.48 ..... \left(1\right)$
مجموع الاحتمالات هو  1	$0.13 + 0.27 + a +b + 0.22 + a = 1$
بجمع الحدود المتشابهة	$2a + b + 0.62 = 1$
بالتبسيط	$2a + b = 0.38 .... \left(2\right)$
بطرح المعادلة (2) من المعادلة (1)	$\mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{1}$
أجد b بتعويض قيمة a في المعادلة (2)	$2(0.1) + b = 0.38 \Rightarrow \mathbf{ }\mathbf{ }\mathit{b}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{18}$

 

 

 

 

 

 

 

 

 

 

 

إذن  :  $P(x = 0) = 0.1 , P(x= 1) = 0.18$

---

 

يتكوَّن مجلس الطلبة في إحدى الجامعات من 8 طلاب و 12 طالبة، وقد اختاروا عشوائيًّا لجنة تضم اثنين منهم للاجتماع مع مُمثِّلين عن رئاسة الجامعة. إذا دلَّ المتغير العشوائي X على عدد الطالبات في اللجنة المختارة، فأُجيب عن الأسئلة الآتية:

3) أُنشِئ جدول التوزيع الاحتمالي.
4) أجد التوقُّع لعدد الطالبات في اللجنة المختارة.
5) أجد التباين للتوزيع الاحتمالي.

الحل : 

3) أُنشِئ جدول التوزيع الاحتمالي. (أستخدم التوافيق لايجاد الاحتمالات لأنّ الترتيب غير مهم)

2	1	0	(x)
0.35	0.5	0.15	P(x)

 

 

 

4) أجد التوقُّع لعدد الطالبات في اللجنة المختارة.

$$\begin{gathered} E\left(x\right) = \sum _{}x . P\left(x\right) \\ = 0\times 0.15 + 1 \times 0.5 + 2\times 0.35 \\ \mathbf{ }\mathbf{\approx }\mathbf{ }\mathbf{1}\mathbf{.}\mathbf{2}\mathbf{ } \\ \mathbf{ } \end{gathered}$$

5) أجد التباين للتوزيع الاحتمالي

$$\begin{gathered} {\sigma }^2 = (\sum _{}{x}^2. P(x\left)\right) - (E{\left(x\right))}^2 \\ =(0^2\times 0.15 + 1^2\times 0.5 + 2^2\times 0.35) - {(1.2)}^2 \\ = 1.9 - 1.44 \\ \mathbf{\approx }\mathbf{ }\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{46} \end{gathered}$$

---

 

 

6) أحُلُّ المسألة الواردة في بند (مسألة اليوم). مسألة اليوم : مثَّلت تغريد التوزيع الاحتمالي لتجربة عشوائية كما في الشكل المجاور، ثم أرادت إيجاد الوسط الحسابي والانحراف المعياري لهذا التوزيع، كيف يُمكِنها ذلك؟

 

 

 

 

 

 

 

 

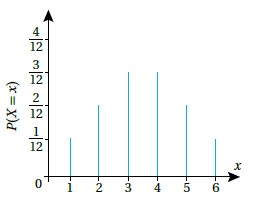الحل : 

الوسط الحسابي	$$\begin{gathered} E\left(x\right) = \sum _{}x . P\left(x\right) \\ = 1\times \frac{1}{12} + 2 \times \frac{2}{12} + 3\times \frac{3}{12} + 4\times \frac{3}{12} + 5\times \frac{2}{12} + 6\times \frac{1}{12} \\ =\frac{42}{12}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{3}\mathbf{.}\mathbf{5} \\ \mathbf{ } \end{gathered}$$
التباين	$$\begin{gathered} {\sigma }^2 = (\sum _{}{x}^2. P(x\left)\right) - (E{\left(x\right))}^2 \\ =(1^2\times \frac{1}{12} + 2^2\times \frac{2}{12} + 3^2\times \frac{3}{12} +4^2\times \frac{3}{12} +5^2\times \frac{2}{12} + 6^2\times \frac{1}{12} ) - {(3.5)}^2 \\ = \frac{170}{12} - 12.25 \\ \mathbf{\approx }\mathbf{ }\mathbf{ }\mathbf{1}\mathbf{.}\mathbf{92} \end{gathered}$$
الانحراف المعياري	${\sigma }^{ }= \sqrt{1.92} \mathbf{ }\mathbf{\approx }\mathbf{ }\mathbf{1}\mathbf{.}\mathbf{39}\mathbf{ }$

 

 

 

 

 

 

 

 

 

 

 

 

 

---

 

7) تحدٍّ : ما قيمة ${\sigma }^2$ للتوزيع الاحتمالي للمتغير العشوائي X في الجدول الآتي إذا كان E(x) = 5.95 ؟

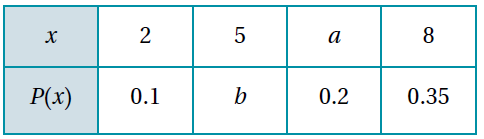
الحل : 

مجموع الاحتمالات = 1	$$\begin{gathered} 0.1 + b + 0.2 + 0.35 = 1 \\ b + 0.65 = 1 \\ \mathit{b}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{35}\mathbf{ } \end{gathered}$$
E(x) = 5.95	$$\begin{gathered} E\left(x\right) = \sum _{}x . P\left(x\right) \\ 5.95 = 2\times 0.1 + 5 \times 0.35 + a\times 0.2 + 8\times 0.35 \\ 5.95 = 0.2 + 1.75 +0.2 a + 2.8 \\ 5.95 = 0.2a + 4.75 \Rightarrow \mathbf{ }\mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{6}\mathbf{ } \\ \mathbf{ } \end{gathered}$$
التباين	$$\begin{gathered} {\sigma }^2 = (\sum _{}{x}^2. P(x\left)\right) - (E{\left(x\right))}^2 \\ =(2^2\times 0.1 + 5^2\times 0.35 + 6^2\times 0.2 +8^2\times 0.35) - {(5.95)}^2 \\ = 38.75 - 35.4025 \\ \mathbf{=}\mathbf{ }\mathbf{ }\mathbf{3}\mathbf{.}\mathbf{3475} \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

8)  تحدٍّ: إذا كان التوزيع الاحتمالي للمتغير العشوائي X مُعرَّفًا على النحو الآتي:

       $\left\{\right(1 , kx) , (2 , \frac{1}{8}) , (3 , \frac{1}{8}) , (4 , kx) , (5 , \frac{1}{8}) , (6 , \frac{1}{8}) \}$

فما قيمة التوقُّع للمتغير x ؟

الحل : 

مجموع الاحتمالات = 1	$$\begin{gathered} k + \frac{1}{8} +\frac{1}{8} +4k + \frac{1}{8} +\frac{1}{8}= 1 \\ 5k + 0.5 = 1 \\ 5k = 0.5 \\ \Rightarrow \mathit{k}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{1} \end{gathered}$$
التوقع E(x)	$$\begin{gathered} E\left(x\right) = \sum _{}x . P\left(x\right) \\ = 1 \times 0.1 + 2 \times 0.125 +3\times 0.125 + 4\times 0.4 + 5 \times 0.125 + 6 \times 0.125 \\ = 0.1 + 0.25 + 0.375 + 1.6 + 0.625 + 0.75 \\ \mathbf{=}\mathbf{ }\mathbf{3}\mathbf{.}\mathbf{7}\mathbf{ } \\ \mathbf{ } \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

---

 

أسئلة كتاب التمارين

يُبيِّن الجدول الآتي جزءًا من التوزيع الاحتمالي للمتغير العشوائي X؛ لأنَّ فيه قيمة مفقودة:

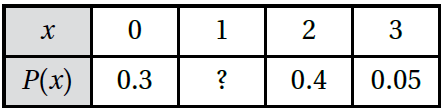
1) أجد القيمة المفقودة في الجدول.

2) أجد التوقُّع E(x). 

الحل : 

1) أجد القيمة المفقودة في الجدول.

أفرض القيمة المفقودة a 

$$\begin{gathered} 0.3 + a + 0.4 + 0.05 = 1 \\ a + 0.27 = 1 \\ \mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{25} \end{gathered}$$

2) أجد التوقُّع E(x). 

$$\begin{gathered} E\left(x\right) = \sum _{}x . P\left(x\right) \\ = 0 \times 0.3 + 1 \times 0.25 + 2\times 0.4 + 3\times 0.05 \\ \mathbf{=}\mathbf{ }\mathbf{ }\mathbf{1}\mathbf{.}\mathbf{2} \\ \mathbf{ } \end{gathered}$$

---

3)  يُبيِّن الجدول الآتي نتائج مسحٍ شمل 100 من طلبة إحدى الجامعات لمعرفة عدد المواد التي سجَّلها الطلبة في فصل دراسي مُعيَّن، بافتراض أنَّ المتغير العشوائي X يُمثِّل عدد المواد المُسجَّلة، أجد التوقُّع E(x). 

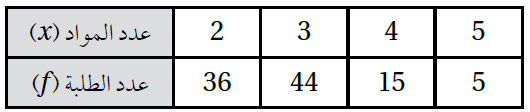
الحل : 

أقسم كل تكرار على مجموع التكرارات، ثم أُنشِئ جدولًا للتوزيع الاحتمالي:

5	4	3	2	(x)
0.05	0.15	0.44	0.36	P(x)

 

 

أجد التوقُّع للمتغير العشوائي x.

$$\begin{gathered} E\left(x\right) = \sum _{}x . P\left(x\right) \\ = 2 \times 0.36 + 3 \times 0.44 + 4\times 0.15 + 5\times 0.05 \\ \mathbf{=}\mathbf{ }\mathbf{ }\mathbf{2}\mathbf{.}\mathbf{89} \\ \mathbf{ } \end{gathered}$$

---

4) إذا كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي، وكان التوقُّع E(x) = 2.2 ، فأجد قيمة كلٍّ من :

P(x = 1) ، P(x = 3).

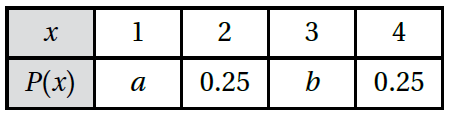
الحل : 

صيغة التوقُّع للمتغير العشوائي x	$E\left(x\right) = \sum _{}x . P\left(x\right)$
لأنَّ التوقُّع هو 2.2	$= 1\times a + 2\times 0.25 + 3 \times b + 4 \times 0.25 = 2.2$
بجمع الحدود المتشابهة	$= a + 3b +1.5 = 2.2$
بالتبسيط	$= a + 3b= 0.7 ....\left(1\right)$
مجموع الاحتمالات هو  1	$a + 0.25 + b + 0.25 = 1$
بجمع الحدود المتشابهة	$a +b + 0.5 =1$
بالتبسيط	$a + b = 0.5 ....\left(2\right)$
بطرح المعادلة (2) من المعادلة (1)	$2b = 0.2 \Rightarrow \mathbf{ }\mathit{b}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{1}\mathbf{ }$
أجد a بتعويض قيمة b في المعادلة (2)	$a + 0.1 = 0.5 \Rightarrow a = 0.4$

 

 

 

 

 

 

 

 

 

 

إذن : $P(x = 1) = 0.4 , P(x= 3) = 0.1$

 

---

 

5) إذا كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي، فأجد التوقُّع E(x)  ، والتباين ${\sigma }^2$. 

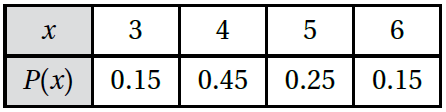
الحل : 

التوقُّع E(x)	$$\begin{gathered} E\left(x\right) = \sum _{}x . P\left(x\right) \\ = 3 \times 0.15 + 4 \times 0.45 + 5\times 0.25 + 6\times 0.15 \\ \mathbf{=}\mathbf{ }\mathbf{ }\mathbf{4}\mathbf{.}\mathbf{4} \\ \mathbf{ } \end{gathered}$$
التباين ${\sigma }^2$	$$\begin{gathered} {\sigma }^2 = (\sum _{}{x}^2. P(x\left)\right) - (E{\left(x\right))}^2 \\ =(3^2\times 0.15 + 4^2\times 0.45 + 5^2\times 0.25 +6^2\times 0.15) - {(4.4)}^2 \\ = 20.2 - 19.36 \\ \mathbf{=}\mathbf{ }\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{84} \end{gathered}$$