أتحققُ من فهمي 1 : أجدُ مساحةَ سطحِ كلِّ كرةٍ ممّا يأتي، وأقربُ إجابتي لأقربِ جزءٍ مِنْ عشرةٍ:
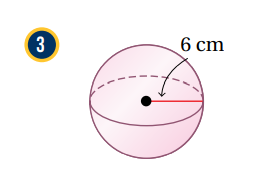 1- نكتب قانون مساحة سطح الكرة :
1- نكتب قانون مساحة سطح الكرة :
2-نعوض قيمة نصف القطر المعطاة بالرسم :
3- باستعمال الآلة الحاسبة نعوض قيمة. وعليه ستكون مساحة سطح الكرة تساوي تقريباً 452.4
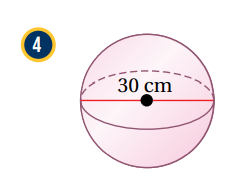 نلاحظ أن المعطى في الشكل هو القطر ويساوي 30 ، لذلك فإن نصف القطر يساوي 15
نلاحظ أن المعطى في الشكل هو القطر ويساوي 30 ، لذلك فإن نصف القطر يساوي 15
1- نكتب قانون مساحة سطح الكرة :
2-نعوض قيمة نصف القطر المعطاة بالرسم :
3- باستعمال الآلة الحاسبة نعوض قيمة
وعليه ستكون مساحة سطح الكرة تساوي تقريباً 2827.4
أتحققُ من فهمي 2 : أجدُ طولَ قُطرِ الكرةِ المجاورةِ إذا علمْتُ أنَّ مساحةَ سطحِها ، وأقرّبُ إجابتي لأقربِ جزءٍ مِنْ عشرة .
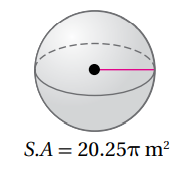
1- نكتب قانون مساحة سطح الكرة :
2-نعوض قيمة مساحة سطح الكرة
3- بقسمة طرفي المعادلة على فتصبح المعادلة :
4-وبأخذ الجذر للطرفين لإيجاد قيمة r فينتج إجابتين لطول نصف القطر
ولأنه لا يوجد طول بالسالب ، فإن الإجابة السالبة ستهمل .
5- نضرب نصف القطر ب 2 لنجد طول القطر ، وعليه فإن طول القطر سيكون 4.5
أتحققُ من فهمي 3 : كرةٌ: يبلغُ محيطُ كرةٍ بلاستيكيةٍ 60cm أجدُ مساحةَ سطحِها التقريبيةَ مقربًا إجابتي لأقربِ عددٍ صحيحٍ.
سنستخدم قانون محيط الدائرة لإيجاد نصف القطر كالتالي :
ثم نستعمل نصف القطر لإيجاد مساحة سطح الكرة .
أتحققُ من فهمي 4 : أجد حجمَ كلِّ كرةٍ أَوْ نصفِ كرةٍ ممّا يأتي، مقرّبًا إجابتي لأقربِ عددٍ صحيحٍ:
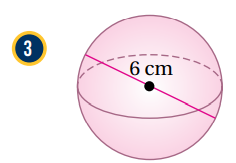
نلاحظ أن المعطى في الشكل هو القطر ويساوي 6 ، لذلك فإن نصف القطر يساوي 3 .
نكتب قانون حجم الكرة ثم نعوض نصف القطر 3.
نكتب قانون حجم نصف الكرة ثم نعوض نصف القطر 6
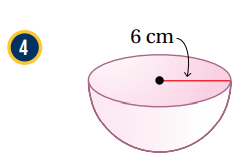
.
أتحققُ من فهمي 5 : أجد حجمَ المجسّمِ المجاورِ، المكوّنِ مِنْ مخروطٍ ارتفاعُهُ 12cm يعلوهُ نصفُ كرةٍ طولُ نصف قطرها 6cm ، مقرّبًا إجابتي لأقربِ جزءٍ مِنْ مئة .
ملاحظة هامة : حجم المخروط = : حيث h الارتفاع.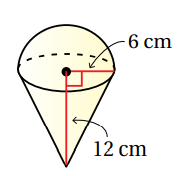
بما أن المجسم يتكون من مخروط + نصف كرة ،فإننا سنجد حجم النصف كرة ونجمعه مع حجم الأسطوانة كما يلي :
أتدرب وأحل مسائل :
أجدُ مساحةَ سطحِ كلِّ كرةٍ أَوْ نصفِ كرةٍ ممّا يأتي، وأقرّبُ إجابتي لأقربِ جزءٍ مِنْ عشرة.
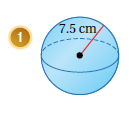
1- نكتب قانون مساحة سطح الكرة :
2-نعوض قيمة نصف القطر المعطاة بالرسم :
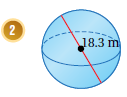
نلاحظ أن المعطى هو القطر ويساوي 18.3 ، وعليه فإن نصف القطر يساوي 9.15
1- نكتب قانون مساحة سطح الكرة :
2-نعوض قيمة نصف القطر المعطاة بالرسم :
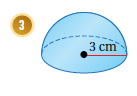
1- نكتب قانون مساحة نصف سطح الكرة :
2-نعوض قيمة نصف القطر المعطاة بالرسم :
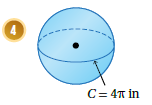 سنستخدم قانون محيط الدائرة لإيجاد نصف القطر كما يلي :
سنستخدم قانون محيط الدائرة لإيجاد نصف القطر كما يلي :
ثم نستعمل نصف القطر لإيجاد مساحة سطح الكرة .
أجدُ طولَ قُطرِ الكرةِ في كلٍّ مِنَ الحالاتِ الآتيةِ، مقرّبًا إجابتي لأقربِ جزءٍ مِنْ عشرةٍ:
5) كرةٌ مساحةُ سطحها 200
الحل:
1- نكتب قانون مساحة سطح الكرة :
2-نعوض قيمة مساحة سطح الكرة :
3- بقسمة طرفي المعادلة على فتصبح المعادلة :
4- بأخذ جذر للطرفين نستنتج أن قيمة نصف القطر
وعليه سيكون طول القطر يساوي 8
6) كرةٌ حجمُها 200
الحل:
نكتب قانون حجم نصف الكرة ثم نعوض الحجم 200
وعليه فإن طول القطر سيساوي 7.3
7) كرةٌ حجمُها 50 .
الحل:
نكتب قانون حجم نصف الكرة ثم نعوض الحجم 50
وعلبه فإن طول القطر سيساوي 4.6
أجدُ حجمَ كلِّ كرةٍ أَوْ نصفِ كرةٍ ممّا يأتي، مقرّبًا إجابتي لأقربِ عددٍ صحيحٍ
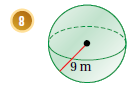
8) نكتب قانون حجم الكرة ثم نعوض نصف القطر 9
9) نكتب قانون حجم نصف الكرة ثم نعوض نصف القطر 5
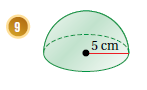
10) نستخدم قانون محيط الدائرة لإيجاد نصف القطر كما يلي : 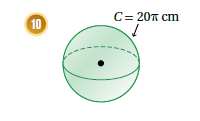
ثم نستخدم قانون حجم الكرة ثم نعوض نصف القطر 10 على النحو التالي :
11) نلاحظ أن المعطى هو القطر ويساوي 14 وبالتالي نصف القطر يساوي 7 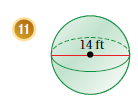
الآن نكتب قانون حجم الكرة ثم نعوض نصف القطر 7
ألعابٌ: يتكوّنُ الجزءُ العُلويُّ مِنْ لعبةِ الغزلِ المجاورةِ مِنْ مخروطٍ ونصفِ كرةٍ. أجدُ بدلالة 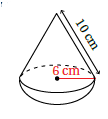
12) حجمَ لعبةِ الغزلِ.
13)المساحةَ الكلّيّةَ لسطحِ لعبةِ الغزلِ.
الحل :
12) لاحظ في البداية أننا لا نعلم ارتفاع المخروط ، لكن بما أن المخروط الدائري قائم فإنه يمكننا إيجاد ارتفاع المخروط باستخدام فيثاغورس .
و بما أن المجسم يتكون من مخروط + نصف كرة ،فإننا سنجد حجم النصف كرة ونجمعه مع حجم المخروط كما يلي :
13) معلومة : مساحة سطح المخروط القائم الجانبية : حيث l هو الارتفاع المائل أو ما يسمى بالراسم.
ولحل السؤال نجمع المساحة الجانبية لسطح المخروط القائم مع مساحة سطح نصف الكرة كالتالي :
14) كرةٌ معدِنيةٌ طولُ نصفِ قُطرِها 15cm ، صُهِرَتْ وأُعيدَ تشكيلُها لأُسطوانةٍ طولُ نصف قطرها 6cm ، أجدُ ارتفاعَ الأُسطوانة .
ملحوظة هامة :
قانون حجم الأسطوانة :
الحل:
بما أن الكرة قد أعيد تشكيلها إلى أسطوانة فإن حجمها يساوي حجم الأسطوانة ، لذلك سنكوّن معادلة نساوي فيها الحجمين لنجد قيمة h
15) مكعبٌ طولُ ضلعِهِ 5cm ، يحتوي نصفَ كرةٍ مفرغةٍ طولُ نصفِ قُطرِها 2.5cm ، أجد حجمَ الجزءِ المتبقّي مِنَ المكعبِ مقرّبًا إجابتي لأقربِ عددٍ صحيحٍ.
ملاحظة : حجم المكعب =
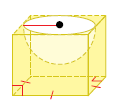
الحل :
بما أن نصف الكرة منحوتة داخل المكعب فسنطرح حجم نصف الكرة من حجم المكعب
16) تبريرٌ: كرةٌ طولُ نصفِ قُطرِها 5cm ، ومخروطٌ طولُ نصفِ قُطرِ قاعدتِهِ 8cm ، إذا كانَ حجمُ الكرةِ وحجمُ المخروطِ متساويَينِ، فأجدُ ارتفاعَ المخروطِ، مبرّرًا إجابتي.
الحل :
سنكوّن معادلة نساوي فيها الحجمين لنجد قيمة h
17) تحدٍّ: تصنعُ شركةٌ كراتٍ صغيرةً مِنَ الفولاذِ المقاومِ للصدأِ (سْتيل) لعجلاتِ الأحذيةِ طولُ قُطرِ كُلِّ مِنْها 4mm ، أجد عددَ الكراتِ الصغيرةِ الّتي يمكنُ للشركةِ تصنيعُها مِنْ 1 مترًا مكعبًا مِنَ (سْتيل).
الحل :
نجد حجم الكرة الصغيرة الواحدة ، محولاً المليمتر إلى متر :
هذا هو حجم الكرة الواحدة بوحدة المتر ، وإذا أردنا معرفة كم كرة يمكن أن نصنع من المتر المكعب الواحد نقوم بالقسم على 1
إذن عدد الكرات التي يمكن صنعها من 1 متر مكعب تساوي
18) تحدٍّ: كرةٌ طولُ قُطرِها 10cm ، نُحِتَتْ مِنْ مكعبٍ خشبيٍّ طولُ ضلعِهِ 10cm ، أحسبُ النسبةَ المئويةَ لكمّيّةِ الخشبِ المهدور
نطرح حجم الكرة من حجم المكعب كالتالي :
إذن ، حجم الخشب المهدور يساوي 476.4
ثم نجد نسبة حجم الخشبة المهدور إلى حجم المكعب كالتالي:
19) أكتب : كيفَ أجدُ مساحةَ سطحِ كُرةٍ وحجمَها إذا علمْتُ طولَ نصفِ قُطرِها؟
باستخدام القوانين التالية :
قانون حجم الكرة :
قانون مساحة سطح الكرة :
أسئلة كتاب التمارين :
أجدُ مساحةَ سطحِ كلِّ كرةٍ أَوْ نصفِ الكرةِ وحجمَها ممّا يأتي. أقرّبُ إجابتي لأقربِ جزءٍ مِنْ عشرةٍ:
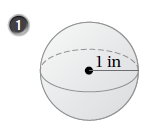 مساحة سطحها :
مساحة سطحها :
حجمها :
مساحة سطحها :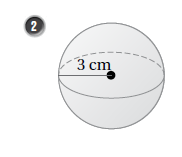
حجمها :
مساحة سطحها : 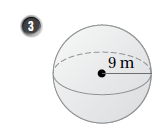
حجمها :
في البداية نجد نصف قطر الكرة باستخدام قانون محيط الدائرة : 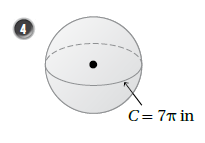
الآن نجد مساحة سطحها :
حجمها :
نجد مساحة سطح نصف الكرة : 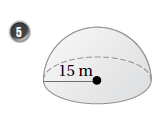
حجم نصف الكرة :
نجد مساحة سطح نصف الكرة : 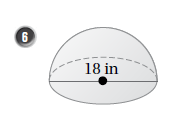
حجم نصف الكرة :
أجدُ مساحةَ سطحِ كلِّ كرةٍ وحجمَها ممّا يأتي بدلالةِ
7) كرةٌ نصفُ قُطرِها 13cm
الحل :
مساحة سطحها
حجمها :
8) كرةٌ محيطُها 30cm
نجد نصف القطر باستخدام قانون محيط الدائرة
الآن يمكننا إيجاد مساحة سطح الكرة وحجمها :
مساحة سطحها :
حجمها :
9) لعبةٌ: لعبةٌ مِنَ البلاستيكِ على شكلِ نصفِ كرةٍ مجوّفةٍ مِنَ الداخلِ كَما في الشكلِ المجاورِ. أجدُ كمّيّةَ البلاستيكِ اللازمةَ لصنعِ الكرةِ.
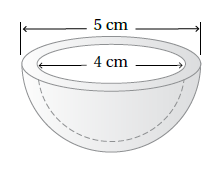
للإيجاد كمية البلاستيك الزمة لصنع اللعبة ،سنقوم بطرح حجم نصف الكرة الصغيرة من حجم نصف الكرة الكبيرة كالتالي :
أجدُ حجمَ كلِّ مجسّمٍ ممّا يأتي:
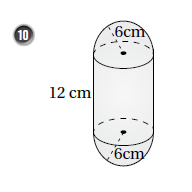 بما أن المجسم يتكون من اسطوانة + نصفي كرة ،فإننا سنجد حجم كرة كاملة ونجمعه مع حجم الأسطوانة كما يلي :
بما أن المجسم يتكون من اسطوانة + نصفي كرة ،فإننا سنجد حجم كرة كاملة ونجمعه مع حجم الأسطوانة كما يلي :
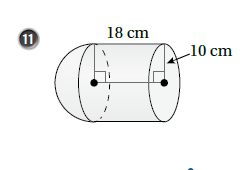
بما أن المجسم يتكون من اسطوانة + نصف كرة ،فإننا سنجد حجم نصف كرة ونجمعه مع حجم الأسطوانة كما يلي
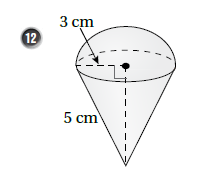
بما أن المجسم يتكون من مخروط+ نصف كرة ،فإننا سنجد حجم نصف كرة ونجمعه مع حجم الأسطوانة كما يلي :
في البداية نجد ارتفاع المخروط باستخدام فيثاغورس .
ثم نجد حجم نصف الكرة + حجمم المخروط كالتالي: