مفهوم أساسي :
الحجمُ (Volume): هُوَ الحيّزُ الّذي يشغَلُهُ الجسمُ في الفضاءِ، وَيُقاسُ بِالوحداتِ المكعَّبَةِ.
المنشورُ (Prism) : مجسَّمٌ كثيرُ السُّطوحِ، لَهُ قاعدتانِ متوازيتانِ وَمتطابقتانِ، وأوجهُهُ الجانبيةُ مستطيلاتُ. وَيسمّى المنشورُ بحسبِ شكلِ قاعدتِهِ.
حجمُ المنشورِ (V) يساوي ناتجَ ضربِ مساحةِ قاعدتِهِ (B) في ارتفاعِهِ (h)
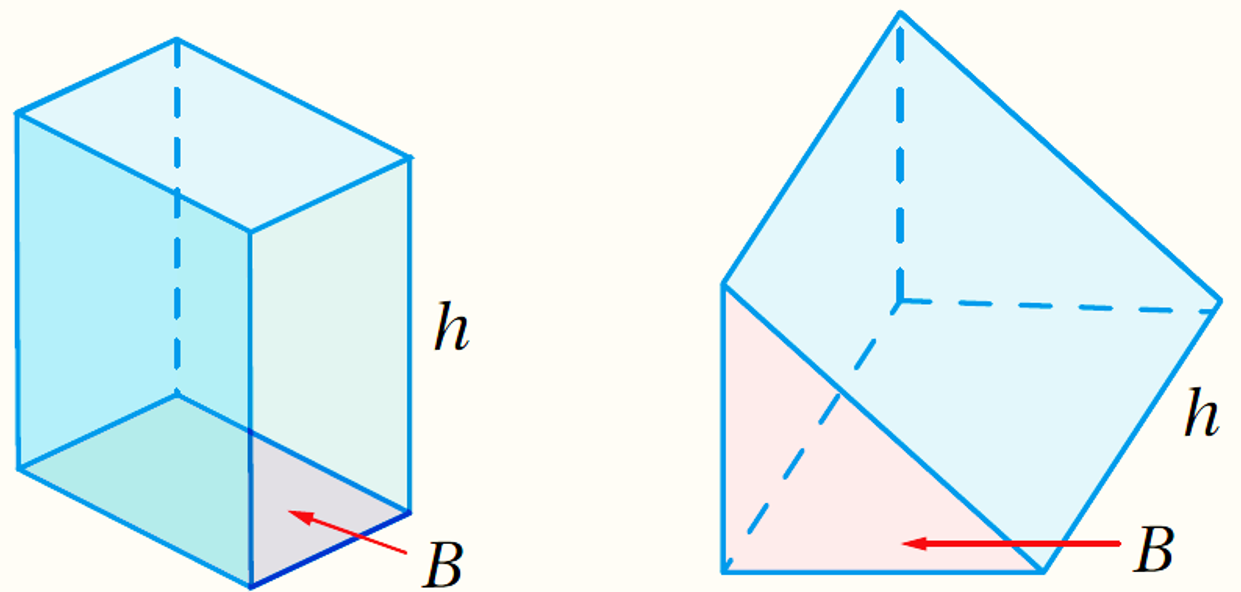
V = Bh
مثال 1: أَجِدُ حجمَ كلِّ منشورٍ ممّا يأتي:
1)
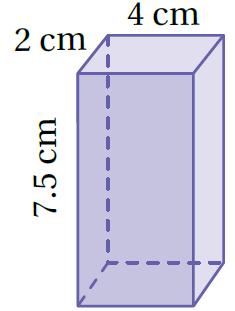
V = Bh صيغة حجم المنشور
(l × w)h = تعويض الأبعاد (القاعدة مستطيلة)
7.5× (4 × 2) =
60 = نجد الناتج
إذنْ، حجمُ المنشورِ يساوي 60cm3
2)
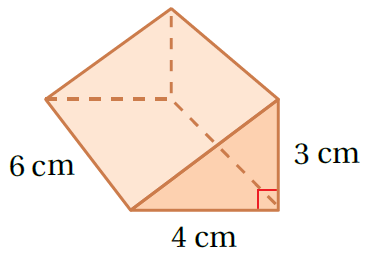
V = Bh صيغة حجم المنشور
تعويض الأبعاد(القاعدة مثلث) ، ثم أجد الناتج
إذنْ، حجمُ المنشورِ يساوي 36cm3
يُمكنُنا استخدامُ قانونِ حجمِ المنشورِ في مواقفَ حياتيةٍ كثيرةٍ ومتنوِّعةٍ.
مثال 3: منَ الحياةِ زراعةٌ: الزراعةُ الرأسيةُ تكونُ في مبانٍ مُكوَّنةٍ مِنْ طوابقَ متعددةٍ يُستغنى فيها عَنِ التربةِ الزراعيةِ. إذا كانَ أحدُ هذهِ المباني على شكلِ منشورٍ قاعدتُهُ مربعةُ الشكلِ طولُ ضلعِها 60m وَارتفاعُهُ 111m أَجِدُ حجمَ المبنى.
V = Bh صيغة حجم المنشور
V = (s2)h تعويض الأبعاد (القاعدة مربعة ضلعها 60m)
إذنْ، حجمُ المبنى 399600m3
مفهوم أساسي :
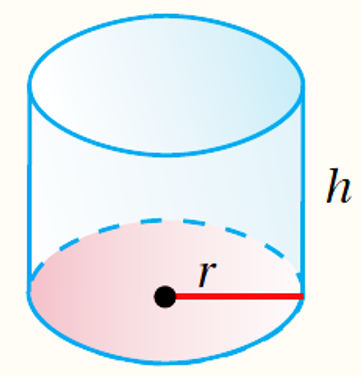
الأُسطوانةُ (Cylinder): هِيَ مجسَّمٌ لَهُ قاعدتانِ دائريتانِ متطابقتانِ وَمتوازيتانِ، ترتبطانِ معًا بسطحٍ مُنحَنٍ، وَارتفاعُ الأسطوانةِ (h) هُوَ المسافةُ العموديةُ بينَ قاعدَتَيْها، وَيسمّى نصفُ قُطرِ القاعدةِ نصفَ قُطرِ الأُسطوانةِ (r)
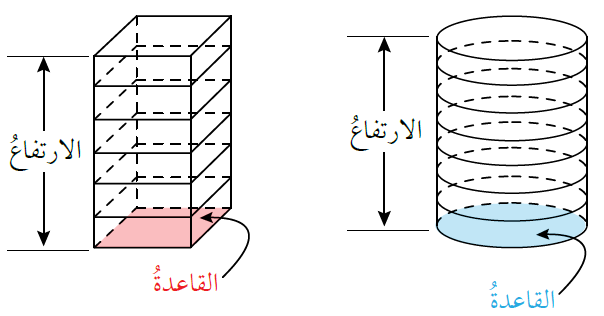
عندَ المقارنةِ بينَ أُسطوانةٍ وَمنشورٍ لَهُما الارتفاعُ نفسُهُ، نلاحظُ أنَّ كلا المجسَّمَيْنِ مكوَّنٌ مِنْ قاعدتَينِ، وَلَوْ قسّمْنا المنشورَ وَالأُسطوانةَ إلى طبقاتٍ لَوجدْنا أنَّ مساحةَ سطحِ كلِّ طبقةٍ مساوٍ لمساحةِ القاعدةِ، وَبما أنَّ ارتفاعَ الطبقاتِ مساوٍ لارتفاعِ المنشورِ والأُسطوانةِ، نستنتجُ أنَّهُ يُمكنُ حسابُ حجمِ الأُسطوانةِ بطريقةٍ مشابهةٍ لِطريقةِ حسابِ حجمِ المنشورِ، وَذلكَ بِضربِ مساحةِ قاعدتِها في ارتفاعِها.
حجمُ الأُسطوانةِ (V) الّتي نصفُ قُطْرِها (r) يساوي ناتجَ ضربِ مساحةِ قاعدتها (B) في ارتفاعها (h)
مثال 3: أَجِدُ حجمَ الأُسطوانةِ المجاوِرةِ وَأُقرّبُ إجابتي لِقربِ جزءٍ مِنْ عشرة
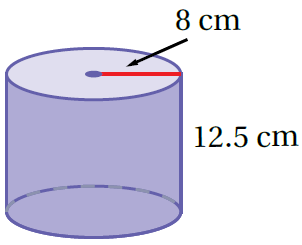
صيغة حجم الأسطوانة
تعويض الأبعاد
أستعملُ الآلةَ الحاسبةَ

إذنْ، حجمُ الأُسطوانةِ يساوي 2513.3cm3 تقريبًا.
يُمكنُنا استخدامُ قانونِ حجمِ الأُسطوانةِ في مواقفَ حياتيةٍ كثيرةٍ وَمتنوِّعةٍ.
مثال 4: منَ الحياةِ صوامعُ: الصّومعةُ الأُسطوانيةُ مبنًى مجهَّزٌ لِتخزينِ الحُبوبِ وَحفظِها في مكانٍ آمنٍ بعيدٍ عَنْ أسبابِ الإتلافِ. أَجِدُ حجمَ صومعةٍ يبلغُ ارتفاعُها 30m وَطولُ قُطرِها 20m وَأُقرّبُ إجابتي لِقربِ جزءٍ مِنْ عشرة.
صيغة حجم الأسطوانة
تعويض الأبعاد، ثم إيجاد الناتج بإستخدام الآلة الحاسبة
إذنْ، حجمُ الصومعةِ يساوي 9424.8m3 تقريبًا.