رياضيات فصل ثاني

مفاهيم أساسية : 

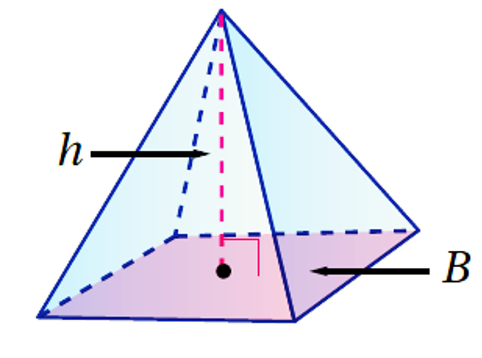
مقارنة : حجمَ الهَرَمِ يساوي ثُلُثَ حجمِ المنشورِ المُساوي لَهُ في مساحةِ القاعدةِ وَالارتفاعِ.

حجمُ الهَرَمِ (V) يساوي ثُلُثَ مساحةِ قاعدتِهِ (B) في ارتفاعهِ (h)

$\mathbf{V}\mathbf{=}\frac{\mathbf{1}}{\mathbf{3}}\mathbf{Bh}$

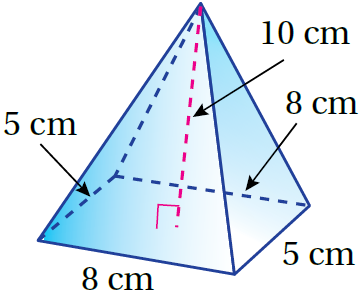
مثال 1: أَجِدُ حجمَ كلِّ هَرَمٍ ممّا يأتي، وَأقرّبُ إجابتي لِقربِ جزءٍ مِنْ مئةٍ:

1)

 

          $\mathrm{V}=\frac{1}{3}\mathrm{Bh}$                            صيغةُ حجمِ الهَرَمِ 

$$\begin{gathered} =\frac{1}{3}\left(l\times w\right)h \\ =\frac{1}{3}\left(8\times 5\right)10 \\ \approx 133.33 \end{gathered}$$                           القاعدة مستطيل وبتعويض الأبعاد أَجِدُ الناتجَ 

 إذنْ، حجمُ الهَرَمِ يساوي 133.33cm³ تقريبًا.

 

يُمكنُنا استخدامُ قانونِ حجمِ الهَرَمِ في مواقفَ حياتيةٍ كثيرةٍ ومتنوِّعةٍ.
مثال 2: منَ الحياةِ محمياتٌ: تتكوّنُ محميةُ موتارت لِلنباتاتِ في كندا مِنْ 4 بيوتٍ زجاجيةٍ كلٌّ منها على شكلِ هَرَمٍ قاعدتُهُ مربعةُ الشكلِ، وَيحتوي كلُّ بيتٍ منها على مُناخٍ مختلِفٍ وَأنواعٍ متباينَةٍ مِنَ النباتاتِ. أَجِدُ حجمَ الهَرَمِ الأكبرِ علمًا أنَّ ارتفاعَهُ 24m وَطولَ ضِلعِ قاعدتِهِ المربعةِ 25m 

       $\mathrm{V}=\frac{1}{3}\mathrm{Bh}$                           صيغةُ حجمِ الهَرَمِ 

$$\begin{gathered} =\frac{1}{3}\left({\mathrm{s}}^2\right)\mathrm{h} \\ =\frac{1}{3}\left({25}^2\right)24 \\ =5000 \end{gathered}$$                          القاعدةُ مربعةٌ، إذنْ، B=s² وبتعويض الأبعاد أَجِدُ الناتجَ 

إذنْ، حجمُ الهَرَمِ يساوي 5000m³

---

مفاهيم أساسية : 

المخروط :هُوَ شكلٌ ثلاثيُّ الأبعادِ، لَهُ قاعدةٌ دائريةٌ واحدةٌ، وَسطحٌ مُنحَنٍ يصلُ القاعدةَ بِالرأسِ. 

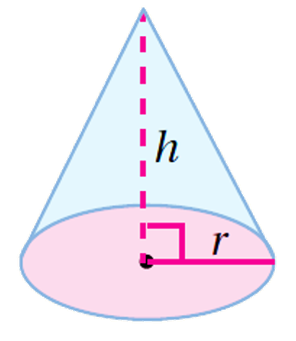
علاقةُ حجمِ المخروطِ بِحجمِ الأُسطوانةِ مثلُ علاقةِ حجمِ الهَرَمِ بِحجمِ المنشورِ، أيْ أنَّ حجمَ المخروطِ يساوي ثُلُثَ حجمِ  الأُسطوانةِ المساويةِ لَهُ في مساحةِ القاعدةِ وَالارتفاعِ.

حجمُ المخروطِ (V)الّذي طولُ نصفِ قُطرِهِ (r) يساوي : ثُلُثَ مساحةِ قاعدتِهِ (B)في ارتفاعِهِ (h)

$\mathbf{V}\mathbf{=}\mathbf{Bh}$  أو  $\mathit{V}\mathbf{=}\frac{\mathbf{1}}{\mathbf{3}}{\mathbf{\pi r}}^{\mathbf{2}}\mathbf{h}$

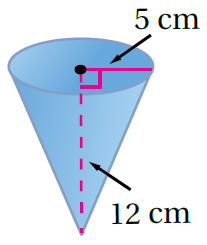
مثال 3: أَجِدُ حجمَ كلِّ مخروطٍ ممّا يأتي، وَأقرّبُ إجابتي إلى أقربِ جزءٍ مِنْ مئةٍ:

1) 

        $\mathrm{V}=\frac{1}{3}{\mathrm{\pi r}}^2\mathrm{h}$                      صيغةُ حجمِ المخروطِ 

$$\begin{gathered} =\frac{1}{3}\mathrm{\pi }{\left(5\right)}^2\left(12\right) \\ \approx 314.16 \end{gathered}$$                       بتعويض الأبعاد أجد الناتج 

إذنْ، حجمُ المخروطِ يساوي 314.16cm³ تقريبًا.

 

يُمكنُنا استخدامُ قانونِ حجمِ المخروطِ في مواقفَ حياتيةٍ كثيرةٍ وَمتنوِّعةٍ.

مثال 4: منَ الحياةِ : ملحٌ: مِنْ طرائقِ إنتاجِ الملحِ شَقُّ أقنيةٍ لِجمعِ المياهِ المالحةِ في مسطَّحاتٍ، ثمَّ ترَكِها لِتجفَّ تحتَ أشعةِ الشمسِ، ثمَّ جمعِ المِلْحِ على شكلِ أكوامٍ مخروطيةِ. إذا كانَ طولُ قُطرِ كَومَةِ ملحٍ 120cm وَارتفاعُها 55cm فأَجِدُ حجمَها. أقرّبُ إجابتي لِأقربِ جزءٍ مِنْ مئةٍ:

بما أنَّ كَومَةَ المِلْحِ على شكلِ مخروطٍ، إذًا أَجِدُ حجمَ المخروطِ.

          $\mathrm{V}=\frac{1}{3}{\mathrm{\pi r}}^2\mathrm{h}$                 صيغةُ حجمِ المخروطِ 

$$\begin{gathered} =\frac{1}{3}\mathrm{\pi }{\left(60\right)}^2\left(55\right) \\ \approx 207345.12 \end{gathered}$$                 بتعويض الأبعاد أجد الناتج 

إذنْ، حجمُ كَومَةِ المِلْحِ يساوي 20735.12cm³ تقريباً