رياضيات9 فصل أول

التاسع

الشرح الملخص أوراق العمل حل اسئلة الدرس النتاجات

حلول أسئلة كتاب الطالب وكتاب التمارين

أسئلة أتحقق من فهمي

أتحقق من فهمي صفحة 117

أُحلل $2 x^{2} + 7 x + 6$

الحل :

بما أنَّ a = 2 , b = 7 , c = 6 ، فأبحثُ عنْ عددَيْنِ حاصلُ ضربِهِما 12 = 6 × 2 ومجموعُهُما 7 .

العددين هما : 4 ، 3

بكتابةِ القاعدةِ	$2 x^{2} + 7 x + 6 = 2 x^{2} + m x + n x + 6$
بتعويض m = 3 , n = 4	$= 2 x^{2} + 3 x + 4 x + 6$
بتجميعِ الحدودِ ذاتِ العواملِ المُشترَكةِ	$= (2 x^{2} + 3 x) + (4 x + 6)$
بتحليل كلِّ تجميع بإخراج العامل المُشترك الأكبر	$= x (2 x + 3) + 2 (2 x + 3)$
بإخراجِ $(2 x + 3)$ عاملًا مُشترَكًا	$= (2 x + 3) (x + 2)$

أتحقق من فهمي صفحة 120

أُحلل كل مما يأتي :

$a) 9 x^{2} - 33 x + 18$

أخرج 3 عاملًا مشتركًا ، ثم أحلل المقدار الجبري :

$3 (3 x^{2} - 11 x + 6)$

بما أنَّ a = 3 , b = -11 , c = 6 ، فأبحثُ عنْ عددَيْنِ حاصلُ ضربِهِما 18 = 6 × 3 ومجموعُهُما 11-

العددين هما 9 - ، 2 -

بكتابةِ القاعدةِ	$3 x^{2} - 11 x + 6 = 3 x^{2} + m x + n x + 6$
بتعويض m = -2 , n = -9	$= 3 x^{2} - 2 x - 9 x + 6$
بتجميعِ الحدودِ ذاتِ العواملِ المُشترَكةِ	$= (3 x^{2} - 2 x) + (- 9 x + 6)$
بتحليل كلِّ تجميع بإخراج العامل المُشترك الأكبر	$= x (3 x - 2) + (- 3) (3 x - 2)$
بإخراجِ $(3 x - 2)$ عاملًا مُشترَكًا	$= (3 x - 2) (x - 3)$

إذن تحليل $9 x^{2} - 33 x + 18$ هو : $3 (3 x - 2) (x - 3)$

$b) 5 x^{2} - 13 x + 6$

بما أنَّ a = 5 , b = -13 , c = 6 ، فأبحثُ عنْ عددَيْنِ حاصلُ ضربِهِما 30 = 6 × 5 ومجموعُهُما 13-

العددين هما 3 - ، 10 -

بكتابةِ القاعدةِ	$5 x^{2} - 13 x + 6 = 5 x^{2} + m x + n x + 6$
بتعويض m = -10 , n = -3	$= 5 x^{2} - 10 x - 3 x + 6$
بتجميعِ الحدودِ ذاتِ العواملِ المُشترَكةِ	$= (5 x^{2} - 10 x) + (- 3 x + 6)$
بتحليل كلِّ تجميع بإخراج العامل المُشترك الأكبر	$= 5 x (x - 2) + (- 3) (x - 2)$
بإخراجِ $(x - 2)$ عاملًا مُشترَكًا	$= (x - 2) (5 x - 3)$

أتحقق من فهمي صفحة 121

أُحلل $3 x^{2} - 3 x - 6$

الحل :

بما أنَّ a = 3 , b = -3 , c = - 6 ، فأجِدُ عددَيْنِ حاصلُ ضربِهِما 18- = 6 - × 3 ومجموعُهُما 3-

العددين هما 6 - ، 3

بكتابةِ القاعدةِ	$3 x^{2} - 3 x - 6 = 3 x^{2} + m x + n x - 6$
بتعويض m = 3 , n = -6	$= 3 x^{2} + 3 x - 6 x - 6$
بتجميعِ الحدودِ ذاتِ العواملِ المُشترَكةِ	$= (3 x^{2} + 3 x) + (- 6 x - 6)$
بتحليل كلِّ تجميع بإخراج العامل المُشترك الأكبر	$= 3 x (x^{} + 1) + (- 6) (x + 1)$
بإخراجِ $(x^{} + 1)$ عاملًا مُشترَكًا	$= (x^{} + 1) (3 x - 6)$

أتحقق من فهمي صفحة 122

أَحلّ كُلّ من المُعادلات الآتية :

$a) 2 x^{2} - 5 x + 2 = 0$

المُعادلة المُعطاة	$2 x^{2} - 5 x + 2 = 0$
بالتحليل إلى العوامل	$(2 x - 1) (x - 2) = 0$
خاصيّة الضرب الصفريّ	$2 x - 1 = 0 o r x - 2 = 0$
بحلّ كلّ مُعادلة	$x = 0.5 o r x = 2$

$b) 2 x^{2} + 6 x = - 4$

المُعادلة المُعطاة	$2 x^{2} + 6 x + 4 = 0$
بقسمة المعادلة على 2	$x^{2} + 3 x + 2 = 0$
بالتحليل إلى العوامل	$(x + 2) (x + 1) = 0$
خاصيّة الضرب الصفريّ	$x + 2 = 0 o r x + 1 = 0$
بحلّ كلّ مُعادلة	$x = - 2 o r x = - 1$

أتحقق من فهمي صفحة 123

محميَّةٌ: محميَّةٌ طبيعيَّةٌ مستطيلةُ الشكلِ يزيدُ طولُها على مِثْلَيْ عرضِها بمقدارِ $1 k m$ . إذا كانتْ مساحتُها $136 k m^{2}$ ، فَأَجِدُ أبعادَها.

الحل :

أفرض عرض المستطيل x ، إذن طوله 2x + 1

مساحة المستطيل = الطول $\times$ العرض ، إذن : $x (2 x + 1) = 136$

أكتب المعادلة بالصورة القياسية وأحللها

$2 x^{2} + x - 136 = 0$

$(2 x + 17) (x - 8) = 0$

$2 x + 17 = 0 o r x - 8 = 0$

$x = - \frac{17}{2} o r x = 8$

تُهمل الإجابة السالبة؛ لأنها مسافة، إذن x = 4

إذن : عرض المحمية $8 k m$ ، وطوله $17 k m$

أسئلة أتدرب وأحل المسائل

أُحلّل كُلًّ ممّا يأتي :

1) 3x² + 11x + 6

$(3 x + 2) (x + 3)$

2) 8x²- 30x + 7

$(2 x - 7) (4 x - 1)$

3) 6x² + 15x - 9

$= 3 (2 x^{2} + 5 x - 3) = 3 (2 x - 1) (x + 3)$

4) 4x² - 4x - 35

$(2 x + 5) (2 x - 7)$

5) 12x² + 36x + 27

$= 4 x^{2} + 12 x + 9 = (2 x + 3) (2 x + 3)$

6) 6r² - 14r - 12

$(r - 3) (6 r + 4)$

أَحلّ كُلًّ من المُعادلات الآتية :

7) 24x² - 19x + 2 = 0

$(3 x - 2) (8 x - 1) = 0$

$3 x - 2 = 0 o r 8 x - 1 = 0$

$x = \frac{2}{3} o r x = \frac{1}{8}$

8) 18t² + 9t + 1 = 0

$(3 t + 1) (6 t + 1) = 0$

$t = - \frac{1}{3} o r t = - \frac{1}{6}$

9) 5x² + 8x + 3 = 0

$(x + 1) (5 x + 3) = 0$

$x + 1 = 0 o r 5 x + 3 = 0$

10) 5x² -9x -2 = 0

$(x - 2) (5 x + 1) = 0$

$x - 2 = 0 o r 5 x + 1 = 0$

$x = 2 o r x = - \frac{1}{5}$

11) 4t² - 4t - 35 = 0

$(2 t + 5) (2 t - 7) = 0$

$2 t + 5 = 0 o r 2 t - 7 = 0$

$t = - 2.5 o r t = 3.5$

12) 6x² + 15x - 9 = 0

$= 2 x^{2} + 5 x - 3$

$(x + 3) (2 x - 1) = 0$

$x + 3 = 0 o r 2 x - 1 = 0$

$x = - 3 o r x = 0.5$

13) 28 s² - 85s + 63 = 0

$(4 s - 7) (7 s - 9) = 0$

$4 s - 7 = 0 o r 7 s - 9 = 0$

$s = \frac{7}{4} o r s = \frac{9}{7}$

14) 9d² - 24d - 9 = 0

$= 3 d^{2} - 8 d - 3$

$(3 d + 1) (d - 3) = 0$

$3 d + 1 = 0 o r d - 3 = 0$

$d = - \frac{1}{3} o r d = 3$

15) 8x(x + 1) = 16

$8 x^{2} + 8 x = 16$

$8 x^{2} + 8 x - 16 = 0$

$x^{2} + x - 2 = 0$

$(x - 1) (x + 2) = 0$

$x - 1 = 0 o r x + 2 = 0$

$x = 1 o r x = - 2$

16) 13x² = 11 - 2x

$13 x^{2} + 2 x - 11 = 0$

$(x + 1) (13 x - 11) = 0$

$x + 1 = 0 o r 13 x - 11 = 0$

$x = - 1 o r x = \frac{11}{13}$

17) 8x - 16 - x² = 0

$- x^{2} + 8 x - 16 = 0$

$x^{2} - 8 x + 16 = 0$

18) 2t² - t = 15

$2 t^{2} - t - 15 = 0$

$(2 t + 5) (t - 3) = 0$

$2 t + 5 = 0 o r t - 3 = 0$

$t = - 2.5 o r t = 3$

19) (2x + 1)(5x + 2) = (2x - 2)(x - 2)

$10 x^{2} + 4 x + 5 x + 2 = 2 x^{2} - 4 x - 2 x + 4$

$10 x^{2} + 9 x + 2 = 2 x^{2} - 6 x + 4$

$8 x^{2} + 15 x - 2 = 0$

$(x + 2) (8 x - 1) = 0$

$x + 2 = 0 o r 8 x - 1 = 0$

$x = - 2 o r x = \frac{1}{8}$

20) 8x² + 6x + 3 = 2x² + x + 2

$8 x^{2} + 6 x + 3 = 2 x^{2} + x + 2$

$6 x^{2} + 5 x + 1 = 0$

$(2 x + 1) (3 x + 1) = 0$

$2 x + 1 = 0 o r 3 x + 1 = 0$

$x = - \frac{1}{2} o r x = - \frac{1}{3}$

هندسة : يُبيّن الشكل المُجاورُ مستطيلًا مساحتُهُ $35 c m^{2}$ ، صنعتهُ شُروق بقصّ أشرطة متساوية

العرض من ورقة مستطيلة الشكل.

21) أجدُ عرض الشريط.

22) أجدُ أبعاد المستطيل الجديد.

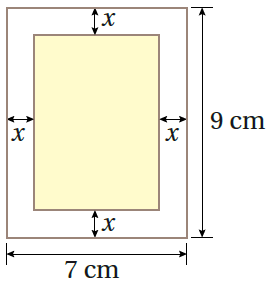الحل :

طول المستطيل الجديد $9 - 2 x$

عرض المستطيل الجديد $7 - 2 x$

مساحة المستطيل = الطول $\times$ العرض

$(9 - 2 x) (7 - 2 x) = 35$

$63 - 18 x - 14 x + 4 x^{2} = 35$

$4 x^{2} - 32 x + 28 = 0$

$x^{2} - 8 x + 7 = 0$

$(x - 1) (x - 7) = 0$

$x - 1 = 0 o r x - 7 = 0$

$x = 1 o r x = 7$

نُهمل x = 7 ؛ لأنها ستجعل كل من العرض والطول سالبًا ، إذن $x = 1$

إذن طول المستطيل الجديد = $7 c m$ ، وعرض المستطيل الجديد = $5 c m$

23) بطاقة : بطاقة دعوة مستطيلة الشكل يزيدُ طولُها على مثلَي عرضها بمقدار $3 c m$ .

إذا كانت مساحتُها $90 c m^{2}$ ، فأجدُ طولها وعرضها.

الحل :

أفرض العرض x ، إذن الطول 2x + 3

مساحة المستطيل = الطول $\times$ العرض

$x (2 x + 3) = 90$

$2 x^{2} + 3 x - 90 = 0$

$(2 x + 15) (x - 6) = 0$

$2 x + 15 = 0 o r x - 6 = 0$

$x = - 7.5 o r x = 6$

يُهمل الحل السالب ، إذن x = 6

عرض بطاقة الدعوة = $6 c m$ وطولها = $15 c m$

24) أحُلّ المسألة الواردة في بداية الدرس.

مسألةُ اليومِ : إذا كانَ الاقترانُ h(t) = -5t² + 7t + 6 يُمَثِّلُ ارتفاعَ غطّاسٍ بالأمتارِ فوقَ سطحِ

الماءِ، بعدَ t ثانيةً مِنْ قفزِهِ عَنْ مِنَصَّةِ القفزِ. فما الزمنُ الذي يستغرقُهُ للوصولِ إلى سطحِ الماءِ؟

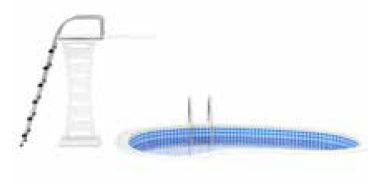الحل :

$- 5 t^{2} + 7 t + 6 = 0$

$5 t - 7 t - 6 = 0$

$(t - 2) (5 t + 3) = 0$

$t - 2 = 0 o r 5 t + 3 = 0$

$t = 2 o r t = - 0.6$

يُهمل الحل السالب ، إذن t = 2

مهاراتُ التفكيرِ العُليا

تبرير : يُبيّن الشكل المُجاور مثلثًا قائم الزاوية.

25) أُبَيّن، بالاعتماد على الشكل، أنَّ 0 = 20x² - 24x - 9 ، مُبرّرًا إجابتي.

إرشادٌ: أستعملُ نظريَّةَ فيثاغورس

26) أَجِدُ مساحةَ المثلَّثِ.

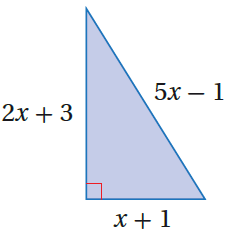الحل :

25) باستخدام نظرية فيثاغورس

${(5 x - 1)}^{2} = {(2 x + 3)}^{2} + {(x + 1)}^{2} 25 x^{2} - 10 x + 1 = 4 x^{2} + 12 x + 9 + x^{2} + 2 x + 1$

$25 x^{2} - 10 x + 1 = 5 x^{2} + 14 x + 10$

$20 x^{2} - 24 x - 9 = 0$

26)

$20 x^{2} - 24 x - 9 = 0$

$(2 x - 3) (10 x + 3) = 0$

$2 x - 3 = 0 o r 10 x + 3 = 0$

$x = 1.5 o r x = - 0.3$

يُهمل الحل السالب ، إذن x = 1.5

مساحة المثلث = $\frac{1}{2}$ القاعدة $\times$ الارتفاع

$= \frac{1}{2} (x + 1) (2 x + 3) = \frac{1}{2} (1.5 + 1) (2 \times 1.5 + 3) = \frac{1}{2} (2.5) (6) = 7.5$

إذن مساحة المثلث = 7.5 وحدة مربعة .

27) أكتشفُ المُختلف: أيُّ المقادير الآتية مُختلفة ؟ أُبَرّر إجابتي.

الإجابة :

جميع المقادير هي تحليل للمقدار الجبري $2 x^{2} + x - 6$

والمختلف $(2 x + 3) (x - 2)$ ، لأنّه تحليل للمقدار الجبري $2 x^{2} - x - 6$

28) تَحَدٍّ : أَجِدُ جميع قِيَمِ الثابت k ؛ حيثُ يمكنُ تحليلُ ثلاثِيِّ الحدودِ 2x² + kx + 12 إلى عاملين باستعمال الأعداد الصحيحة.

الحل :

قيم k هي مجموع أزواج عوامل العدد 24

1 ، 24 أو 2 ، 12 أو 3 ، 8 أو 4 ، 6

إذن : قيم k هي : 25 ، 14 ، 11 ، 10

أسئلة كتاب التمارين

أُحَلِّلُ كُلًّ ممّا يأتي :

1) 3n² + 5n - 2 2) 2x² + 3x + 1 3) 3x² - x - 2

4) 5b² - 13b + 6 5) 30x² - 25x - 30 6) 21x² + 2x - 3

الحل :

1) 3n² + 5n - 2

$(3 n - 1) (n + 2)$

2) 2x² + 3x + 1

$(2 x + 1) (x + 1)$

3) 3x² - x - 2

$(3 x + 2) (x - 1)$

4) 5b² - 13b + 6

$(5 b - 3) (b - 2)$

5) 30x² - 25x - 30

$= 5 (6 x^{2} - 5 x - 6) = 5 (3 x + 2) (2 x - 3)$

6) 21x² + 2x - 3

$(7 x + 3) (3 x - 1)$

أَحُلُّ المُعادلات الآتية بالتحليل :

7) 3x² + 8x - 3 = 0 8) 3t² - 14t + 8 = 0 9) 6x² - 5x - 4 = 0

10) 24x² - 19x + 2 = 0 11) 15k² + 4k - 35 = 0 12) 6x²+30 = 5 - 3x² - 30x

13) 2k² - 5k - 18 = 0 14) 12m² + 11m = 15 15) 40n² - 70n + 15 = 0

الحل :

7) 3x² + 8x - 3 = 0

$(3 x + 1) (x - 3) = 0$

$3 x + 1 = 0 o r x - 3 = 0$

$x = - \frac{1}{3} o r x = 3$

8) 3t² - 14t + 8 = 0

$(3 t - 2) (t - 4) = 0$

$3 t - 2 = 0 o r t - 4 = 0$

$t = \frac{2}{3} o r t = 4$

9) 6x² - 5x - 4 = 0

$(2 x + 1) (3 x - 4) = 0$

$2 x + 1 = 0 o r 3 x - 4 = 0$

$x = - \frac{1}{2} o r x = \frac{4}{3}$

10) 24x² - 19x + 2 = 0

$(8 x - 1) (3 x - 2) = 0$

$8 x - 1 = 0 o r 3 x - 2 = 0$

$x = \frac{1}{8} o r x = \frac{2}{3}$

11) 15k² + 4k - 35 = 0

$(5 x - 7) (3 x + 5) = 0$

$5 x - 7 = 0 o r 3 x + 5 = 0$

$x = \frac{7}{5} o r x = - \frac{5}{3}$

12) 6x²+30 = 5 - 3x² - 30x

$9 x^{2} + 30 x + 25 = 0$

$(3 x + 5) (3 x + 5) = 0$

$3 x + 5 = 0 \to x = - \frac{5}{3}$

13) 2k² - 5k - 18 = 0

$(2 k - 9) (k + 2) = 0$

$2 k - 9 = 0 o r k = - 2$

$k = 4.5 o r k = - 2$

14) 12m² + 11m = 15

$12 m^{2} + 11 m - 15 = 0$

$(3 m + 5) (4 m - 3) = 0$

$3 m + 5 = 0 o r 4 m - 3 = 0$

$m = - \frac{5}{3} o r m = \frac{3}{4}$

15) 40n² - 70n + 15 = 0

$8 n^{2} - 14 n + 3 = 0$

$(2 n - 3) (4 n - 1) = 0$

$2 n - 3 = 0 o r 4 n - 1 = 0$

$n = \frac{3}{2} o r n = \frac{1}{4}$

هندسةٌ : مُعتَمِدًا الشكلَ المُجاورَ ، أَحُلُّ السؤالَيْنِ الآتِيَيْنِ تِباعًا:

16) أَجِدُ مساحةَ المُستطيلِ المُجاورِ بدلالةِ x.

17) إذا كانَتْ مساحةُ المُستطيلِ 40 وحدةٍ مُرَبَّعَةٍ ، فَأَجِدُ قيمةَ x.

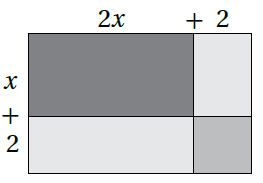الحل:

16) مساحة المستطيل = الطول $\times$ العرض

$(2 x + 2) (x + 2) = 2 x^{2} + 6 x + 4$

17)

$2 x^{2} + 6 x + 4 = 40$

$2 x^{2} + 6 x - 36 = 0$

$x^{2} + 3 x - 18 = 0$

$(x + 6) (x - 3) = 0$

$x + 6 = 0 o r x - 3 = 0$

$x = - 6 o r x = 3$

يُهمل الحل السالب ، إذن x = 3

18) رياضة : إذا كان الاقترانُ h(t) = -16t² + 8t + 24 يُمَثِّل ارتفاع غطّاس بالأقدام فوق سطح الماء، بعد t ثانية من قفزه عن مِنصَّة القفز، فما الزمن الذي يستغرقُه للوصول إلى سطح الماء؟

الحل :

$- 16 t^{2} + 8 t + 24 = 0$

$4 t^{2} - 2 t - 6 = 0$

$(2 t - 3) (2 t + 2) = 0$

$2 t - 3 = 0 o r 2 t + 2 = 0$

$t = 1.5 o r t = - 1$

يهمل الحل السالب ، إذن t =1.5 ، أي الزمن الذي سيستغرقه الغطاس للوصول إلى سطح الماء بعد 1.5 ثانية

19) أكتشِفُ الخطأَ: أكتشِفُ الخطأَ في الحلِّ الآتي، وَأُصَحِّحُهُ.

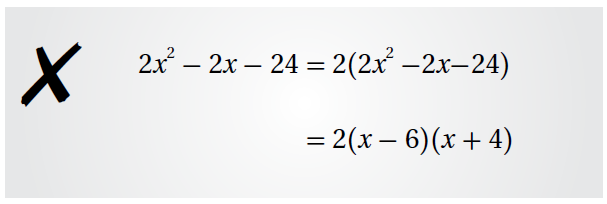
الإجابة :

بإخراج 2 عامل مشترك يجب أن نقسم كل حد من حدود المقدار الجبري على العامل المشترك ، والحل الصحيح كالتالي :

$2 x^{2} - 2 x - 24 = 2 (x^{2} - x - 12) = 2 (x - 4) (x + 3)$

رياضيات9 فصل أول

التاسع

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS