حلول أسئلة كتاب الطالب وكتاب التمارين
أسئلة أتحقق من فهمي
أتحقق من فهمي صفحة 145
أَحُلّ كلّ من المُعادلات الآتية :
a) x3 + 12x = 7x2
| المُعادلةُ المُعطاةُ | x3 + 12x = 7x2 |
| بِطرحِ 7x2 من طَرَفَيِ المُعادلةِ | x3 - 7x2+ 12x = 0 |
| بالتحليلِ بإخراجِ العاملِ المُشترَكِ الأكبرِ | x(x2 - 7x + 12) = 0 |
| بالتحليلِ إلى العوامل | x(x - 3)(x - 4) = 0 |
| خاصيَّةُ الضَّربِ الصِّفريِّ | x = 0 or x - 3 = 0 or x - 4 = 0 |
| حلِّ كلِّ مُعادلةٍ | x = 0 or x = 3 or x = 4 |
b) x3 = 25x
| المُعادلةُ المُعطاةُ | x3 = 25x |
| بِطرحِ 25x من طَرَفَيِ المُعادلةِ | x3 - 25x = 0 |
| بالتحليلِ بإخراجِ العاملِ المُشترَكِ الأكبرِ | x(x2 - 25) = 0 |
| بتحليل فرق بين مربعين | x(x - 5)(x + 5) = 0 |
| خاصيَّةُ الضَّربِ الصِّفريِّ | x = 0 or x - 5 = 0 or x + 5 = 0 |
| حلِّ كلِّ مُعادلةٍ | x = 0 or x = 5 or x = -5 |
أتحقق من فهمي صفحة 146
أَحُلّ كلّ مِنَ المُعادلات الآتية :
a) 9x3 + 18x2 + 2x + 4 = 0
| المُعادلةُ المُعطاةُ | 9x3 + 18x2 + 2x + 4 = 0 |
| بتجميعِ الحُدودِ ذاتِ العواملِ المُشترَكَةِ | (9x3 + 18x2 ) + (2x + 4) = 0 |
| بتحليلِ كلِّ تجميعٍ بإخراجِ العاملِ المُشترَكِ الأكبرِ | 9x2(x + 2) + 2(x + 2) = 0 |
| بإخراجِ ( x + 2 ) عاملًا مُشترَكًا | (x + 2)(9x2+ 2) = 0 |
| خاصيَّةُ الضَّربِ الصِّفريِّ | x + 2 = 0 or 9x2+ 2 = 0 |
| بحلِّ المُعادلةِ | x = - 2 |
بما أنَّهُ لا يوجدُ حلٌّ حقيقيٌّ للمُعادلةِ 9x2 + 2 ، فإنَّ للمُعادلةِ الأصليَّةِ جذرًا وحيدًا هُوَ 2 -
b) 2x3 + x2 - 14x - 7 = 0
| المُعادلةُ المُعطاةُ | 2x3 + x2 - 14x - 7 = 0 |
| بتجميعِ الحُدودِ ذاتِ العواملِ المُشترَكَةِ | (2x3 + x2 ) + (-14x - 7) = 0 |
| بتحليلِ كلِّ تجميعٍ بإخراجِ العاملِ المُشترَكِ الأكبرِ | x2(2x + 1) + -7(2x + 1) = 0 |
| بإخراجِ (2x + 1) عاملًا مُشترَكًا | (2x + 1)(x2- 7) = 0 |
| خاصيَّةُ الضَّربِ الصِّفريِّ | 2x + 1 = 0 or x2- 7 = 0 |
| بحلِّ كل معادلة | x = or x = |
أتحقق من فهمي صفحة 148
أَحُلّ كلّ مِنَ المُعادلات الآتية :
a) 27x3 - 1 = 0
| المُعادلة المُعطاة | 27x3 - 1 = 0 |
| بكتابة المقدار على صورة الفرق بين مُكعّبين | |
| بتحليل الفرق بين مُكَعّبين | |
| خاصيَّة الضّرب الصّفريّ | |
| بحلّ المُعادلة |
بما أنَّهُ لا يوجدُ حلٌّ حقيقيٌّ للمُعادلةِ 9x2 + 3x + 1 ، فإنَّ للمُعادلةِ الأصليَّةِ جذرًا وحيدًا هُوَ 2 -
b) x3 + 1000 = 0
| المُعادلةُ المُعطاةُ | x3 + 1000 = 0 |
| بالكتابةِ على صورةِ مجموعِ مُكَعَّبَيْنِ | |
| بتحليلِ مجموعِ مُكَعَّبَيْنِ | |
| خاصيَّةُ الضَّربِ الصِّفريِّ | |
| بحلِّ المُعادلةِ |
بما أنَّهُ لا يوجدُ حلٌّ حقيقيٌّ للمُعادلةِ x2 - 10x + 100 ، فإنَّ للمُعادلةِ الأصليَّةِ جذرًا وحيدًا هُوَ 10 -
c) 16x4 - 250x = 0
| المُعادلة المُعطاة | 16x4 - 250x = 0 |
| بإخراج 2x عامل مشترك | 2x(8x3 - 125) = 0 |
| بتحليل الفرق بين مُكَعّبين | 2x(2x - 5)(4x2 + 10x + 25) = 0 |
| خاصيَّة الضّرب الصّفريّ | 2x = 0 or 2x - 5 = 0 or 4x2 + 10x + 25 |
| بحلّ كل مُعادلة | x = 0 or x = 2.5 |
بما أنَّهُ لا يوجدُ حلٌّ حقيقيٌّ للمُعادلةِ 4x2 + 10x + 25 ، فإنَّ للمُعادلةِ الأصليَّةِ جذران حقيقيان هما 2.5 ، 0
أتحقق من فهمي صفحة 149
أَحُلّ كلّ مِنَ المُعادلات الآتية :
a) x4 - 625 = 0
| المُعادلة المُعطاة | x4 - 625 = 0 |
| بكتابة المعادلة على الصورة التربيعيّة | |
| بتحليلِ فرق بين مربعين | |
| خاصيَّةُ الضَّربِ الصِّفريِّ | |
| بحل المعادلة | |
| بالتبسيط |
بما أنَّهُ لا يوجدُ حلٌّ حقيقيٌّ للمُعادلةِ x2 + 5 = 0 ، فإنَّ للمُعادلةِ الأصليَّةِ جذران حقيقيان هما 5 - ، 5
b) x4 - 3x2 + 2 = 0
| المُعادلة المُعطاة | x4 - 3x2 + 2 = 0 |
| بكتابة المعادلة على الصورة التربيعيّة | |
| بالتحليلِ إلى العواملِ | |
| خاصيَّةُ الضَّربِ الصِّفريِّ | |
| بحل كل معادلة |
للمعادلة 4 جذور ، هي :
أتحقق من فهمي صفحة 150
|
صناعةٌ : تصنعُ شركةٌ صناديقَ لجهازِ إلكترونيٍّ على شكلِ مُتوازي مستطيلاتٍ، أبعادُها كما هُوَ مُبَيَّنٌ في الشكلِ المُجاورِ. إذا كانَ حجمُ الصندوقِ ، فَأَجِدُ أبعادَهُ. |
 |
الحل :
حجم متوازي المستطيلات = الطول العرض الارتفاع
أحل المعادلة بالتجميع
| المُعادلةُ المُعطاةُ | x3 + 3x2 -16x - 48 = 0 |
| بتجميعِ الحُدود ذات العوامل المُشتركة | (x3 + 3x2) + (-16x - 48) = 0 |
| بتحليلِ كلِّ تجميعٍ بإخراجِ العاملِ المُشترَكِ الأكبرِ | x2(x + 3) -16(x + 3) = 0 |
| بإخراجِ (x + 3) عاملًا مُشترَكًا | (x + 3)(x2 -16) = 0 |
| خاصيَّةُ الضَّربِ الصِّفريِّ | x + 3 = 0 or x2 - 16 = 0 |
| حلِّ كلِّ مُعادلةٍ | x = -3 or x = 4 or x = -4 |
يُهمل الحل السالب ، إذن x = 4
الطول = ، العرض = ، الارتفاع =
أسئلة أتدرب وأحل المسائل
أَحُلّ كلّ مِنَ المُعادلات الآتية :
| 1) 3x4 - 12x3 = 0 | 2) 35x3 - 28x2 - 7x = 0 | 3) 6x6 - 3x4 - 9x2 = 0 |
| 4) 2x3 + 4x2 + 2x = 0 | 5) 3x3 = 12x | 6) x3 + 4x2 + 4x = 0 |
| 7) 2x3 -3x2 - 4x + 6 = 0 | 8) 10x3 -15x2 + 2x -3 = 0 | 9) x3 - 3x2 + x - 3 = 0 |
| 10) 125x3 - 1 = 0 | 11) 3x3 + 3000 = 0 | 12) x4+ x3 - 12x - 12 = 0 |
| 13) 5x3 - 320 = 0 | 14) x4 - 5x2 + 4 = 0 | 15) 2x4 - 9x2 + 4 = 0 |
| 16) 4x4 + 20x2 = -25 | 17) 16x4 - 81 = 0 | 18) 5w6 - 25w3 + 30 = 0 |
الحل :
|
1) 3x4 - 12x3 = 0 |
أحل المعادلة بإخراج العامل المشترك الأكبر للمعادلة جذران هما: 0 ، 4 |
|
إخراج العامل المشترك الأكبر ثم أحل المعادلة التربيعية باستخدام القانون العام إذن للمعادلة الأصلية 3 جذور هي : 0 ، 1 ، 0.2 - |
2) 35x3 - 28x2 - 7x = 0
|
|
إخراج العامل المشترك الأكبر ثم أكتب المعادلة التي أعلى أس فيها 4 على الصورة التربيعيّة ، ثم أحللها . إذن للمعادلة الأصلية 3 جذور هي : |
3) 6x6 - 3x4 - 9x2 = 0
|
|
إخراج العامل المشترك الأكبر ثم أحل المعادلة التربيعية بالتحليل إلى العوامل للمعادلة الأصلية جذران هما : 0 ، 1- |
4) 2x3 + 4x2 + 2x = 0 |
|
كتابة المعادلة بالصورة القياسية ، ثم إخراج العامل المشترك الأكبر ، ثم تحليل الفرق بين المربعين للمعادلة الأصلية 3 جذور ، هي : 0 ، 2 ، 2- |
5) 3x3 = 12x
|
|
إخراج العامل المشترك الأكبر ثم أحل المعادلة التربيعية بالتحليل إلى العوامل للمعادلة الأصلية جذران هما : 0 ، 2- |
6) x3 + 4x2 + 4x = 0
|
|
أحل المعادلة بالتجميع للمعادلة الأصلية 3 جذور ، هي : |
7) 2x3 -3x2 -4x +6 = 0
|
|
أحل المعادلة بالتجميع ألاحظ أن المعادلة 5x2 + 1 = 0 ليس لها حل لأن مميزها عدد سالب إذن ، للمعادلة الأصلية جذر واحد ، هو : 1.5 |
8) 10x3 -15x2 + 2x-3 = 0 |
|
أحل المعادلة بالتجميع ألاحظ أن المعادلة x2 + 1 = 0 ليس لها حل لأن مميزها عدد سالب إذن ، للمعادلة الأصلية جذر واحد ، هو : 3
|
9) x3 - 3x2 + x - 3 = 0
|
|
بتحليل الفرق بين مُكَعّبين ، وألاحظ المعادلة التربيعية الناتجة من تحليل الفرق بين مكعبين أولية لا تُحلل لأنّ مميزها عدد سالب إذن للمعادلة الأصلية جذر واحد هو : 0.2 |
10) 125x3 - 1 = 0
|
|
قسمة طرفي المعادلة على 3 ، ثم تحليل مجموع مكعبين وألاحظ أن المعادلة التربيعية الناتجة من تحليل مجموع مكعبين أولية لا تُحلل لأنّ مميزها عدد سالب إذن للمعادلة الأصلية جذر واحد هو 10 - |
11) 3x3 + 3000 = 0
|
| أحل المعادلة بالتجميع ، إذن للمعادلة الأصلية جذران هما : |
12) x4+ x3 -12x -12 = 0 |
|
قسمة المعادلة على 5 ، ثم تحليل فرق مكعبين ، العبارة التربيعية الناتجة من تحليل فرق مكعبين أولية لا تحلل لأنّ مميزها عدد سالب إذن للمعادلة الأصلية جذر واحد ، هو 4 |
13) 5x3 - 320 = 0
|
|
أكتب المعادلة على الصورة التربيعيّة ، ثم أحللها . للمعادلة الأصلية 4 جذور ، هي : 1 ، 1- ، 2 ، 2- |
14) x4 - 5x2 + 4 = 0
|
|
أكتب المعادلة على الصورة التربيعيّة ، ثم أحللها . للمعادلة الأصلية 4 جذور ، هي : ، 2 ، 2-
|
15) 2x4 - 9x2 + 4 = 0 |
|
أكتب المعادلة بالصورة القياسية أفرض ، وأحلل المعادلة أعوض عن u بـ المعادلة ليس لها حلول حقيقية إذن لا يوجد حل للمعادلة . |
16) 4x4 + 20x2 = -25 |
|
تحليل المعادلة فرق بين مربعين ، وألاحظ أنّ المعادلة أولية لأنّ مميزها عدد سالب إذن للمعادلة الأصلية جذران ، هما :
|
17) 16x4 - 81 = 0 |
|
أقسم طرفي المعادلة على 5 ، ثم أكتب المعادلة على الصورة التربيعيّة ، ثم أحللها . للمعادلة الأصلية جذران ، هما : |
18) 5w6 - 25w3 + 30 = 0 |
|
19) مشاريعُ صغيرةٌ : يُمَثِّلُ الاقترانُ R(t) = t3 - 8t2 + t + 15 الإيرادَ السنويَّ (بالألفِ دينارٍ)لمشروعِ غيداءَ الصغيرِ بعدَ t عامًا مِنْ إنشائِهِ. بعدَ كمْ سنةً يصلُ إيرادُ غيداءَ إلى 23 ألفَ دينارٍ؟ |
 |
الحل :
أجعل الاقتران الذي يمثل الايراد يساوي 23 (بالألف دينار)
المعادلة t2 + 1 = 0 ليس لها حل لأنّ مميزها سالب ، إذن t = 8 ، إذن بعد 8 سنوات يصبح إيراد غيداء 23 ألف.
|
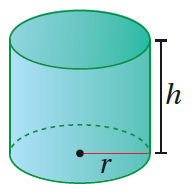
20) هندسةٌ : يُبَيِّنُ الشكلُ المُجاورُ أُسطوانةً حجمُها . إذا كانَ طولُ نصفِ قطرِ قاعدةِ الأُسطوانةِ يقلُّ عَنِ ارتفاعِها بمقدارِ ، فَأَجِدُ أبعادَها. |
 |
الحل:
طولُ نصفِ قطرِ قاعدةِ الأُسطوانةِ يقلُّ عَنِ ارتفاعِها بمقدارِ ، إذن h = r + 3
حجم الأسطوانة = مساحة القاعدة الارتفاع
أعوض بدلًا من h بـ r + 3
أقسم طرفي المعادلة على
أبسط وأكتب المعادلة بالصورة القياسية ، وأحل المعادلة بالتجميع :
يُهمل الحل السالب ، إذن
21) أَحُلُّ المسألةَ الواردةَ في بدايةِ الدرسِ.
|
مسألةُ اليومِ : كيسٌ للهدايا على شكلِ مُتوازي مستطيلاتٍ، حجمُهُ ، وأبعادُهُ بدلالةِ المُتَغَيِّرِ w مُوَضَّحَةٌ في الشكلِ المُجاورِ. أَجِدُ أبعادَهُ. |
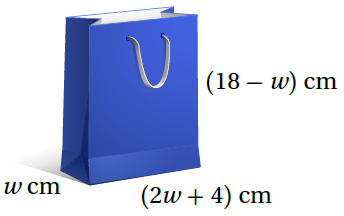 |
الحل :
حجم متوازي المستطيلات = الطول العرض الارتفاع
أحل المعادلة بالتجميع
يُهمل الحل السالب ، إذن w = 16 أو w = 6
إذا كان w = 6 ، أبعاد كيس الهدايا هي : (الأبعاد أقرب لشكل الكيس المرسوم)
إذا كان w = 16 ، أبعاد كيس الهدايا هي : (الأبعاد بعيدة عن شكل الكيس المرسوم)
مهاراتُ التفكيرِ العُليا
22) أكتشِفُ الخطأَ : حَلَّتْ نداءُ المُعادلةَ 0 = 2x4 -18x2 ، كما هُوَ مُبَيَّنٌ أدناهُ. أكتشِفُ الخطأَ في حلِّها وَأُصَحِّحُهُ.
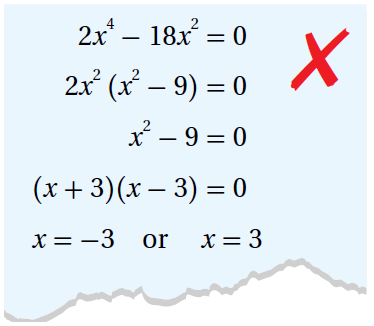
الحل :
أخطأت نداء إذ لم تُطبق خاصية الضرب الصفري بين 2x2 والمقدار (x2 - 9)
والحل الصحبح :
تَحَدّ : أَحُلّ المُعادلتين الآتيتين، مُبرّرًا إجابتي:
23) x6 + 4x3 = 2
| أكتب المعادلة على الصورة التربيعية | |
| أفرض u = x3 | |
| أحل المعادلة بإكمال المربع ، وأجد قيم u مقربًا إجابتي لأقرب جزء من مئة | |
| أعوض بدلًا من u بـ x3 لأجد قيم x مقربًا إجابتي لأقرب جزء من مئة |
24) (x2 - 1)2 - 2(x2 - 1) = 3
| أفرض أنّ ، وأكتب المعادلة بالصورة القياسية | |
| أحل المعادلة بالتحليل إلى العوامل | |
| أعوض بدلًا u بـ ، لأجد قيم x |
25) تبريرٌ : أجِدُ قيمة العدد w التي تجعلُ للمُعادلة 5x3 + wx2 + 80x = 0 حَلّين حقيقيَّيْن فقط ، مُبَرِّرًا إجابتي.
الحل :
| أُخرج العامل المشترك الأكبر | x (5x2 + wx + 80) = 0 |
| بحسب خاصية الضرب الصفري نحصل على حل حقيقي هو x = 0 | x = 0 or 5x2 + wx + 80 = 0 |
|
لنحصل على حل واحد من المعادلة التربيعية 5x2 + wx + 80 = 0 نجعل المميز = صفر |
|
| إذن : w = 40 أو w = - 40 |
أسئلة كتاب التمارين
أَحُلّ المُعادلات الآتية :
1) 24x3 + 18x2 = 0
| أحل المعادلة بإخراج العامل المشترك الأكبر |
2) x3 - 2x2 - 24x = 0
|
أحل المعادلة بإخراج العامل المشترك الأكبر ، ثم أحلل العبارة التربيعية بالتحليل إلى العوامل |
3) 3x5 = 192x3
|
أحل المعادلة بإخراج العامل المشترك الأكبر ، ثم أحلل فرق بين مربعين |
4) 2x3 - 20x2 + 5x - 50 = 0
|
أحلل المعادلة بالتجميع ، وألاحظ أنّ المعادلة 2x2 + 5 = 0 أولية لا تُحلل لأنّ مميزها عدد سالب |
5) x3 - 5x2 + 6x = 30
|
أكتب المعادلة بالصورة القياسية وأحلل بالتجميع وألاحظ أنّ المعادلة x2 + 6 = 0 أولية لا تُحلل لأنّ مميزها عدد سالب |
6) 16x3 + 32x2 - x - 2 = 0
| أحلل بالتجميع |
7) x3 + 512 = 0
|
أحلل مجموع مكعبين ، والعبارة التربيعية الناتجة من تحليل مجموع مكعبين أولية لا تحلل لأنّ مميزها عدد سالب . |
8) 3x9 - 192x6 = 0
|
إخراج العامل المشترك الأكبر ، ثم تحليل الفرق بين مكعبين والعبارة التربيعية الناتجة من تحليل الفرق بين مكعبين أولية لا تحلل لأنّ مميزها عدد سالب . |
9) 3x + 1 = x2 + 3x3
| أحلل بالتجميع |
10) 2x5 + 2x4 - 144x3 = 0
| إخراج العامل المشترك الأكبر ، ثم تحليل إلى العوامل |
11) x4 - 3x2 - 28 = 0
|
أكتب المعادلة على الصورة التربيعية ، ثم أحلل المعادلة x2 + 4 = 0 أولية لا تحلل لأن مميزها عدد سالب . |
12) 16x4 - 81 = 0
|
أحلل فرق بين مربعين ، والمعادلة التربيعية 4x2 + 9 = 0 أولية لا تحلل لأن مميزها عدد سالب . |
13) 4x12 - 32x7 + 48x2 = 0
|
إخراج العامل المشترك الأكبر ، ثم كتابة المعادلة على الصورة التربيعية وتحليلها |
14) 4x3 - 7x2 - 16x + 28 = 0
| أحلل بالتجميع |
15) 4x4 - 25 = 0
|
أحلل المعادلة فرق بين المربعين ، والمعادلة التربيعية 2x2 + 5 = 0 الناتجة أولية لا تحلل لأنّ مميزها عدد سالب . |
|
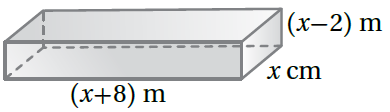
16) هندسةٌ : يُبَيِّنُ الشكلُ المُجاورُ مُتوازي مستطيلاتٍ حجمُهُ أَجِدُ أبعادَهُ. |
 |
الحل :
حجم متوازي المستطيلات = الطول العرض الارتفاع
يُهمل الحل السالب ، إذن x = 4 ، إذن أبعاد الشكل :
| 17) أكتبُ مُعادلةً مُرتبطةً بمنحنى الاقترانِ المُمَثَّلِ بيانِيًّا في الشكلِ المُجاورِ ، مُبَرِّرًا إجابتي. | 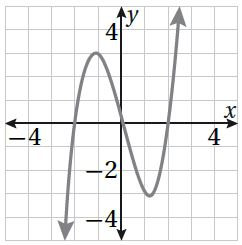 |
الحل :
للمعادلة ثلاثة جذور هي : 2 ، 2- ، 0
إذن :
إذن عوامل الاقتران هي :
المعادلة المرتبط بالاقتران هي :
| 18) حوضُ أسماكٍ : يُبَيِّنُ الشكلُ المُجاورُ حوضًا للأسماكِ على شكلِ مُتوازي مستطيلاتٍ حجمُهُ . أَجِدُ أبعادَهُ. |
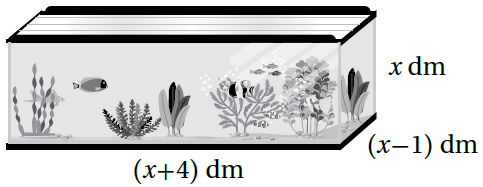 |
الحل :
حجم متوازي المستطيلات = الطول العرض الارتفاع
يُهمل الحل السالب ، إذن x = 2 ، إذن أبعاد حوض الأسماك هي :