رياضيات10 فصل أول

أتحقق من فهمي صفحة 101

أحل المعادلتين الآتيتين، علما بأن $0°\le x\le 360°$: 

$a) 2cosx=\sqrt[]{3}$

$cosx=\frac{\sqrt[]{3}}{2}$

$\frac{\sqrt[]{3}}{2} \mathrm{لها} \mathrm{التمام} \mathrm{جيب} \mathrm{التي} x \mathrm{الزاوية} \mathrm{هي} \mathrm{من}$

$x=co{s}^{-1}\left(\frac{\sqrt[]{3}}{2}\right)=30°$

$\mathrm{الرابع} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{موجب} \mathrm{التمام} \mathrm{جيب}$

$x=360-30=330°$

 

$b) 2tanx+3=1$

$2tanx=1-3=-2$

$tanx=\frac{-2}{2}=1$

$-1 \mathrm{يساوي} \mathrm{ظلها} \mathrm{التي} x \mathrm{الزاوية} \mathrm{هي} \mathrm{من}$

$x=ta{n}^{-1}(-1)$

$x=-45° \mathrm{الحاسبة} \mathrm{بالالة}$

$x=360-45=315° \mathrm{ان} \mathrm{يعني} \mathrm{وهذا}$

$\mathrm{الثاني} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{سالب} \mathrm{الظل}$

$x=180-45=135°$

---

أتحقق من فهمي صفحة 102

أحل المعادلتين الآتيتين: 

$a) 3\left(sin x-2\right)=3-sin x,0°\le x\le 360°$

$3(3 sinx+2)=3-sinx$

$3sinx+6=3-sinx$

$3sinx+sinx=3-6$

$4\sin x=-3\to \sin x=\frac{-3}{4}$

$x={\sin }^{-1}\left(\frac{-3}{4}\right)=-48.6$

$x=360-48.6=311.4°$

$\mathrm{الثالث} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{سالب} \mathrm{جيب}$

$x=180+48.6=228.6°$

 

$b) 3 cos \left(2x\right)-1=0,0°\le x\le 180°$

$3 cos2x-1=0$

$3cos2x=1$

$cos2x=\frac{1}{3}$

$2x=co{s}^{-1}\left(\frac{1}{3}\right)$

$2x=70.5° \Rightarrow x=35.25°$

$2x=360-70.5°=289.5° \Rightarrow x=144.75°$

---

أتحقق من فهمي صفحة 104

أحل المعادلتين الآتيتين، علما بأن $0°\le x\le 360°$:

$a) 4sinx tanx+3tanx=0$

$tanx(4sinx+3)=0$

$tanx=0 or (4sinx+3)=0$

$tanx=0 or sinx=\frac{-3}{4}$

$x=ta{n}^{-1}\left(0\right) or x=si{n}^{-1}\left(\frac{-3}{4}\right)$

$x=0,180,360 or x=-48.6$

$x=0,180,360 or x=360-48.6=311.4,180+48.6=228.6$

 

$b) 2 co{s}^{2}x-3 cos x+1=0$

$(2 cos x-1)(cos x-1)=0$

$(2 cos x-1)=0 or (cos x-1)=0$

$cos x=\frac{1}{2} or cos x=1$

$x=co{s}^{-1}\left(\frac{1}{2}\right) or x=co{s}^{-1}\left(1\right)$

$x=60,300 or x=0,360$

 

---

أتحقق من فهمي صفحة 105

فيزياء: فرق الجهد E (بالفولت) في دارة كهربائية يعطى بالعلاقة: $E =20 \cos \left(180t\right)$، حيث t الزمن (بالثواني): 

a) افترض أن $x=180 t$، واحل المعادلة $12=20 \cos x$، علما بأن $0°\le x\le 360°$

$12=20 cos\left(180t\right)$

$cos\left(180t\right)=\frac{12}{20}=\frac{3}{5}$

$180t=co{s}^{-1}\left(\frac{3}{5}\right)$

$180t=53.13 or 180t=360-53.13=306.87$

$t=\frac{53.13}{180} or t=\frac{306.87}{180}$

$so x=180\times \frac{53.13}{180} or t=180\times \frac{306.87}{180}$

$so x=53.13 or x=306.87$

b) أجد الزمن $\left(0\le t\le 2\mathrm{حيث}\right)t$ عندما يكون فرق الجهد $12 volt$، مقربا إجابتي إلى أقرب جزء من مئة من الثانية 

$12=20 cos\left(180t\right)$

$cos\left(180t\right)=\frac{12}{20}=\frac{3}{5}$

$180t=co{s}^{-1}\left(\frac{3}{5}\right)$

$180t=53.13 or 180t=360-53.13=306.87$

$t=\frac{53.13}{180} or t=\frac{306.87}{180}$

$t\approx 0.30 or t\approx 1.70$

---

أتدرب وأحل المسائل صفحة 106

أحل المعادلات الآتية، علما بأن $0°\le x\le 360°$: 

$1) \sin x=\frac{1}{\sqrt[]{2}}$

$x=45°$

$\mathrm{الثاني} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{موجب} \mathrm{جيب}$

$x=180-45=135°$

 

$2) \tan x= \frac{1}{\sqrt[]{3}}$

$x=30°$

$\mathrm{الثالث} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{موجب} \mathrm{ظل}$

$x=180+30=210°$

 

$3) \cos x=\frac{\sqrt[]{3}}{2}$

$x=30°$

$\mathrm{الرابع} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{موجب} \mathrm{تمام} \mathrm{جيب}$

$x=360-30=330°$

 

$4) 7+9 \cos x= 1$

$9 \cos x=-6$

$\cos =\frac{-6}{9}=\frac{-2}{3}$

$x={\cos }^{-1}\left(\frac{-2}{3}\right)=131.8$

$1800-131.8=48.2 \mathrm{هي} \mathrm{المرجع} \mathrm{الزاوية}$

$\mathrm{الثالث} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{سالب} \mathrm{تمام} \mathrm{جيب}$

$x=180+48.2=228.2°$

 

$5) 2 \sin x+1=0$

$\sin x=\frac{-1}{2}$

$x=150$

$180-150=30 \mathrm{هي} \mathrm{المرجع} \mathrm{الزاوية}$

$\mathrm{الثالث} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{سالب} \mathrm{جيب}$

$x=180+30=210°$

$\mathrm{الرابع} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{سالب} \mathrm{جيب}$

$x=360-30=330°$

 

$6) 1-2 \tan x=5$

$-2 tan x=4$

$tan x=-2$

$x= ta{n}^{-1}(-2)=-63.4$

$x=360-63.4=296.6 \mathrm{هي} \mathrm{الاولى} \mathrm{الزاوية}$

$63.4 \mathrm{هي} \mathrm{المرجع} \mathrm{الزاوية}$

$\mathrm{الثاني} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{سالب} \mathrm{ظل}$

$x=180-63.4=116.6°$

أحل المعادلات الآتية، علما بأن $0°\le x\le 90°$: 

$7) 5-2 \cos \left(4x\right)=4$

$-2 \cos \left(4x\right)=-1$

$\cos \left(4x\right)=\frac{1}{2}$

$4x={\cos }^{-1}\left(\frac{1}{2}\right)=60$

$x=\frac{60}{4}=15 \mathrm{هي} \mathrm{الاولى} \mathrm{الزاوية}$

$\mathrm{الرابع} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{موجب} \mathrm{تمام} \mathrm{جيب}$

$4x=360-60=300°$

$x=\frac{300°}{4}=75°$

 

$8) 3+4 \tan \left(2x\right)=6$

$4 \tan \left(2x\right)=3\to \tan \left(2x\right)=\frac{3}{4}$

$2x={\tan }^{-1}\left(\frac{3}{4}\right)=36.9$

$x=\frac{36.9}{2}=18.5 \mathrm{هي} \mathrm{الأولى} \mathrm{الزاوية}$

$\mathrm{الثالث} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{موجب} \mathrm{ظل}$

$2x=180+36.9=216.9°$

$x=\frac{216.9°}{2}=108.5°$

$\mathrm{السؤال} \mathrm{شرط} \mathrm{حسب} 0\le x\le 90 \mathrm{لان} \mathrm{مرفوضة} \mathrm{وهي}$

 

$9) 13 \sin \left(3x\right)+1=6$

$13 sin \left(3x\right)=5$

$sin \left(3x\right)=\frac{5}{13}$

$3x=si{n}^{-1}\left(\frac{5}{13}\right)=22.6$

$x=\frac{22.6}{3}=7.5 \mathrm{هي} \mathrm{الاولى} \mathrm{الزاوية}$

$\mathrm{الثاني} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{موجب} \mathrm{جيب}$

$3x=180-22.6=157.4°$

$x=\frac{157.4°}{3}=52.5°$

 

أحل المعادلات الآتية، مفترضا أن قياس الزاوية المجهولة يقع الفترة $\left[0°,360°\right]$:

$10) 2\left(\sin x-2\right)+1=3 \sin x$

$2(sin x-2)+1=3sin x$

$2sin x-4+1=3 sin x$

$sin x=-3$

$\mathrm{للمعادلة} \mathrm{حل} \mathrm{يوجد} \mathrm{لا} \mathrm{بالتلي} \mathrm{مستحيل} \mathrm{وهذا}$

 

$11) tan x-3(2 tan x-1)=10$

$tan x-3(2 tan x-1)=10$

$tan x-6tan x+3=10$

$-5tan x=7$

$tan x=\frac{-7}{5}$

$x=ta{n}^{-1}\left(\frac{-7}{5}\right)\approx -54.5$

$54.5 \mathrm{هي} \mathrm{المرجع} \mathrm{الزاوية}$

$x=180-54.5=125.5 \mathrm{الثاني} \mathrm{الربع} \mathrm{في} \mathrm{سالب} \mathrm{ظل}$

$\mathrm{الرابع} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{سالب} \mathrm{ظل}$

$x=360-54.5=305.5°$

 

$12) 15 tan x-7=5 tan x-3$

$10 tan x=4$

$tan x=\frac{4}{10}=\frac{2}{5}$

$x=ta{n}^{-1}\left(\frac{2}{5}\right)\approx 21.8$

$\mathrm{الثالث} \mathrm{الربع} \mathrm{في} \mathrm{ايضا} \mathrm{موجب} \mathrm{ظل}$

$x=180+21.8=201.8°$

 

$13) 5 (cos x-1)=6+cos x$

$5 cos x-5=6+cos x$

$5 cos x-cos x=6+5$

$4cos x=11$

$cos x=\frac{11}{4}=2\frac{3}{4}$

$\mathrm{للمعادلة} \mathrm{حل} \mathrm{يوجد} \mathrm{لا} \mathrm{بالتالي} \mathrm{مستحيل} \mathrm{وهذا}$

 

$14) ta{n}^{2}x-9 tan x+20=0$

$(tan x-5)(tan x-4)=0$

$tan x=5 or tan x=4$

$x=ta{n}^{-1}5 or x=ta{n}^{-1}4$

$x=78.7 or x=76$

$also x=180+78.7=258.7 or x=180+76=256$

$15) 2co{s}^{2}x-cos x=0$

$cos x(2 cos x-1)=0$

$cos x=0 or 2 cos x-1=0$

$cos x=0 or cos x=\frac{1}{2}$

$x=90,270 or x=60,300$

$16) 4 si{n}^{2}x-3 sin x=1$

$4 si{n}^{2}x-3 sin x-1=0$

$(4 sin x+1)(sin x-1)=0$

$(4 sin x+)=0 or (sin x)=0$

$sin x=\frac{-1}{4} or sin x=1$

$x=si{n}^1\left(\frac{-1}{4}\right) or x=90$

$x=-14.5 or x=90$

$x=14.5 \mathrm{هي} \mathrm{المرجع} \mathrm{الزاوية}$

$x=180+14.5=194.5 or x=360-14.5=345.5 or x=90$

 

$17) 2 si{n}^{2}x-1=0$

$2 si{n}^{2}x=1\to si{n}^{2}x=\frac{1}{2}$

$sin x=+\frac{1}{\sqrt[]{2}} or sin x=-\frac{1}{\sqrt[]{2}}$

$x=si{n}^{-1}\left(\frac{1}{\sqrt[]{2}}\right) or x=si{n}^{-1}\left(\frac{-1}{\sqrt[]{2}}\right)$

$x=45,x=180-45=135 or x=-45$

$45 \mathrm{هي} \mathrm{المرجع} \mathrm{الزاوية}$

 

$18) 4 co{s}^{2}x-4=15cos x$

$4 co{s}^{2}x-15 cos x-4=0$

$(4 cos x+1)(cos x-4)=0$

$(4 cos x+1)=0 or (cos x-4)=0$

$cos x=\frac{-1}{4} or cos x=4\left(\mathrm{مستحيل}\right)$

$x=co{s}^{-1}\left(\frac{-1}{4}\right)$

$x=104.5$

$180-104.5=75.5 \mathrm{هي} \mathrm{المرجع} \mathrm{الزاوية}$

$x=180+75.5=225.5 \mathrm{ايضا} \mathrm{بالتالي}$

 

$19) cos x= sin x$

$(\mathrm{جدا} \mathrm{مهم})\mathrm{الاشارات} \mathrm{بسبب} \mathrm{والثالث} \mathrm{الاول} \mathrm{الربع} \mathrm{في} \mathrm{التمام} \mathrm{جيب} \mathrm{يساوي} \mathrm{الجيب}$

$cos x=sin x$

$x=45° ,225°$

20) ساعات: أحل المسألة الواردة في بداية الدرس 

ساعة حائط كبيرة معلقة على جدار غرفة. إذا كان طول عقرب الساعات فيها $16 cm$، وبعد رأس العقرب عن سقف الغرفة يمثل دائما بالعلاقة:$d=-60 \cos \left(30x\right)+110$، حيث: d البعد بالسنتيمتر، و x الوقت بالساعات، فما الوقت الذي يبعد فيه رأس عقرب الساعات $118 cm$عن السقف؟ 

$118=-60 cos\left(30x\right)+110$

$118-110=-60 cos\left(30x\right)$

$\frac{-8}{60}=cos\left(30x\right)$

$30 x=co{s}^{-1}\left(\frac{-8}{60}\right)$

$30x=97.7$

$180-97.7=82.3 \mathrm{هي} \mathrm{المرجع} \mathrm{الزاوية}$

$30 x=97.7 or 30x=180+82.3=262.3$

$x=\frac{97.9}{30} or x=\frac{262.3}{30}$

$x=3.3 or x=8.7$

21) سباحة: سبح حامد مسافة $90 m$ من النقطة A على الضفة الشمالية لنهر إلى النقطة B على الضفة المقابلة، قم دار بزاوية قائمة، وسبح مسافة $60 m$ إلى نقطة أخرى C على الضفة الشمالية. إذا كان قياس الزاوية $CAB$ هو $\theta$، وقياس الزاوية $\left(90°-\theta \right) \mathrm{هو} ACB$، وطول العمود من B إلي CA يساوي عرض النهر d،فأعبر عن d بدلالة $\theta$ مرة، وبدلالة $\left(90°-\theta \right)$ مرة أخرى، ثم اكتب معادلة واحلها لإيجاد قيمة $\theta$، ثم أجد عرض النهر 

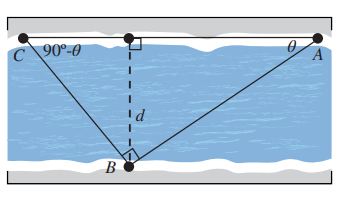
الحل:

$sin \theta =\frac{\mathrm{المقابل} }{\mathrm{الوتر}}=\frac{d}{AB}\Rightarrow d=AB sin \theta \Rightarrow d=90 sin \theta$ 

$sin (90-\theta )=\frac{\mathrm{المقابل} }{\mathrm{الوتر}}=\frac{d}{CB}\Rightarrow d=CB sin(90-\theta )\Rightarrow d=60 sin(90-\theta )$

$d=90 sin \theta =60 sin(90-\theta ) \mathrm{بالتالي}$

$90 sin \theta =60 sin (90-\theta ) \mathrm{بالتالي}$

$90 sin \theta =60 cos \theta$

$sin \theta =\frac{60}{90}cos \theta$

$\frac{sin \theta }{cos \theta }=\frac{\frac{6}{9} cos \theta }{cos \theta }$

$tan \theta =\frac{2}{3}$

$\theta =ta{n}^{-1}\left(\frac{2}{3}\right)$

$\theta =33.6$

$d=90 sin 33.6=90\times 0.55=49.5 m$

 

22) دولاب: يعطى ارتفاع الراكب عن الأرض في دولاب دوار بالمعادلة: $h=27-25\cos \theta$، حيث h الارتفاع بالأمتار، و $\theta$ قياس الزاوية التي دارها الدولاب. متى يكون ارتفاع الراكب عن الأرض $49 m$؟ 

$49=27-25 soc \theta$

$25 cos \theta =27-49$

$25 cos \theta =-22$

$cos \theta =\frac{-22}{25}$

$cos \theta =co{s}^{-1}\left(\frac{-22}{25}\right)$

$\theta =151.6$

$180-151.6=28.4 \mathrm{هي} \mathrm{المرجع} \mathrm{الزاوية}$

$also \theta =180+28.4=208.4$

23) حركة مقذوفات: المسافة الأفقية التي تقطعها مقذوفة في الهواء (من دون افتراض وجود لمقاومة الهواء)تعطى بالعمادلة: $d=\frac{v_0^2\sin \left(2\theta \right)}{g}$، حيث: $v_0$ السرعة الابتدائية، والزاوية التي تطلق بها المقذوفة، و g تسارع الجاذبية الأرضية $\left(9.8 m/s^2\right)$. إذا قذفت كرة بيسبول بسرعة ابتدائية مقدارها $40m/s$، فما الزاوية التي توجه بها الرمية لكي تقطع الكرة مسافة أفقية مقدارها $110m$قبل سقوطها على الأرض؟ ما أبعد نقطة يمكن أن تصلها الكرة إذا قذفت بهذه السرعة الابتدائية؟ 

$110=\frac{{\left(40\right)}^{2}sin \left(2\theta \right)}{9.8}$

$\frac{110\times 9.8}{1600}=sin\left(2\theta \right)$

$\Rightarrow sin \left(2\theta \right)=0.674$

$2\theta =si{n}^{-1}(0.674)$

$2\theta =42.4 or 2\theta =180-42.4=137.6$

$\mathrm{عندئذ}،\theta =45 \mathrm{عندما} \mathrm{نقطة} \mathrm{ابعد} \mathrm{المقذوف} \mathrm{يصل}$

$d=\frac{{\left(40\right)}^{2}sin\left(90\right)}{9.8}=\frac{1600\times 1}{9.8}=163.3m$

مهارات التفكير العليا 

24) اكتشف الخطأ: حل كل من سعيد وعلي المعادلة: $2 \sin x \cos x=\sin x$، حيث:$0°\le x\le 360°$: 

أيهما إجابته صحيحة؟ أبرر إجابتي 

حل سعيد صحيح لانه اخذ sin x عامل مشترك

حل علي خاطئ لانه قسم على sin x وهذا يؤدي الي حذف حلول للمعادلة

 

25) تحد: أحل المعادلة: $2 \sin x \cos x+ \sin x+2 \cos x+1=0$، علما بأن $0°\le x\le 360°$

$2 sin x cos x+sin x+2 cos x+1=0$

$sin x\left(2cos x+1\right)+\left(2cos x+1\right)=0$

$(2 cos x+1)(sin x+1)=0$

$cos x=\frac{-1}{2} or sin x=-1$

$x=co{s}^{-1}\left(\frac{-1}{2}\right) or x=si{n}^{-1}(-1)$

$\Rightarrow x=120,x=240 or x=270$

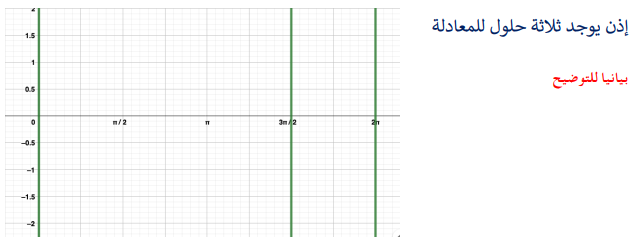
26) تحد: أحدد عدد حلول المعادلة: $\cos x-\sin x-1=0$، حيث:$0°\le x\le 360°$

$cos x- sin x=1$

$cos x=1,sin x=0 or cos x=0,sin x=-1$

$x=0,x=360 or x=270$

---

كتاب التمارين صفحة 24

احل كلا من المعادلات المثلثية الاتية في القترة $\left[0°,360°\right]$: 

$1) sin \mathrm{x}=\frac{1}{3}\to x=si{n}^{-1}\frac{1}{3}\approx 19° or x\approx 161°$

$2) tan \mathrm{x}=\sqrt[]{3}\to x=ta{n}^{-1}\sqrt[]{3}=60° or x=240°$

$3) cos \mathrm{x}=-\frac{\sqrt[]{3}}{3}\to x=co{s}^{-1}\frac{-\sqrt[]{3}}{3}\approx 125° or x\approx 235°$

$4) cos \mathrm{x}=-\frac{1}{2}\to x=co{s}^{-1}\frac{-1}{2}=120° or x=240°$

$5) tan \mathrm{x}=-\frac{1}{\sqrt[]{2}}\to x=ta{n}^{-1}\frac{-1}{\sqrt[]{2}}=150° or x=330°$

$6) 2sin \mathrm{x}+3=1$

$2sin x=-2\Rightarrow sin x= -1$

$x=si{n}^{-1}-1=270°$

$7) \sqrt[]{2} cos \mathrm{x}+1=2$

$\sqrt[]{2}cos x=1\Rightarrow cos x=\frac{1}{\sqrt[]{2}}$

$x=co{s}^{-1}\frac{1}{\sqrt[]{2}}=45° or x= 315°$

 

$$\begin{gathered} 8) \sqrt[]{3} tan \mathrm{x}+4=1 \\ \sqrt[]{3} tan x=-3\Rightarrow tan x=\frac{-3}{\sqrt[]{3}}=-\sqrt[]{3} \\ x=ta{n}^{-1}-\sqrt[]{3}=120° or x=300° \\ 9) 3 tan \mathrm{x}+2=7-2tan \\ 5tan x =5 \Rightarrow tan x =1 \\ x=ta{n}^{-1}1=45° or x=225° \\ 10) 5-3sin \mathrm{x}=sin \mathrm{x}+1 \\ -4 sin x=-4\Rightarrow sin x=1 \\ x=si{n}^{-1}1=90° \\ 11) 2(3 sin \mathrm{x}+1)+2=4sin \mathrm{x}+5 \\ 2 sin x=1\Rightarrow sin x=\frac{1}{2} \\ x=si{n}^{-1 }\frac{1}{2}=30° or x=150° \\ 12) 3(2-cos \mathrm{x})+4=5cos \mathrm{x}+2 \\ 8=8cos x\Rightarrow cos x=1 \\ x=co{s}^{-1}1=0° or x=360° \\ 13) 3+2cos\left(3\mathrm{x}\right)=1,0°<\mathrm{x}<120° \\ 2cos 3x=-2\Rightarrow cos 3x=-1 \\ 3x=co{s}^{-1}-1=180°\Rightarrow x=60° \\ 14) 5+2tan\left(4\mathrm{x}\right)=7,0°<\mathrm{x}<90° \\ 2 tan 4x=2\Rightarrow tan 4x=1 \\ 4x = ta{n}^{-1}1=45 \Rightarrow x=11.25° \\ or 4x=225 \Rightarrow x=56.25° \\ 15) 4sin \mathrm{x} cos \mathrm{x}+3sin \mathrm{x}=0 \\ \sin x(4\cos x+3)=0 \\ \sin x=0\Rightarrow x=0° or x=180° \\ 4\cos x=-3\Rightarrow \cos x=\frac{-3}{4}\Rightarrow x\approx 138.59° or x\approx 221.41° \\ 16) 2 cos \mathrm{x} sin \mathrm{x}=cos \mathrm{x} \\ cos \mathrm{x}(2sin \mathrm{x}-1)=0 \\ cos \mathrm{x}=0\Rightarrow \mathrm{x}=90° or \mathrm{x}=270° \\ 2sin \mathrm{x}=1\Rightarrow sin \mathrm{x}=\frac{1}{2}\Rightarrow \mathrm{x}= 30° or \mathrm{x}= 150° \\ 17) 4si{n}^2\mathrm{x}=1 \\ sin x=\frac{\pm 1}{2}\Rightarrow \begin{array}{r}sin x=\frac{1}{2}\Rightarrow x=30° or x=150°\\ sin x =\frac{-1}{2}\Rightarrow x=210° or x=330°\end{array}\} \\ 18) ta{n}^2\mathrm{x}-9=0 \\ tan x =\pm 3\Rightarrow \begin{array}{r}tan x=3\Rightarrow x \approx 71.57° or x=251.57°\\ tanx =-3\Rightarrow x\approx 108.43° or x\approx 288.43°\end{array}\} \\ 19) 2co{s}^2\mathrm{x}-3 cos \mathrm{x}+1=0 \\ (2cosx-1)(cos x-1)=0 \\ 2cos x=1\Rightarrow cos x=\frac{1}{2}\Rightarrow x=60° or x=300° \\ cos x=1\Rightarrow x=0° or x=360° \\ 20) 2si{n}^2\mathrm{x}+5sin \mathrm{x}+2=0 \\ (2sin x+1)(sin x+2)=0 \\ 2sin x=-1\Rightarrow sin x=\frac{-1}{2}\Rightarrow x=210° or x=330° \\ sinx =-2 \mathrm{مرفوض} \\ 21) 2ta{n}^2\mathrm{\theta }-5tan \mathrm{\theta }-3=0 \\ (2tan \theta +1)(tan \theta -3)=0 \\ 2tan \theta =-1\Rightarrow tan\theta =\frac{-1}{2}\Rightarrow \theta \approx 153.43° or \theta \approx 333.43° \\ tan \theta =3\Rightarrow \theta \approx 153.43 or \theta \approx 71.57° or \theta \approx 251.57° \\ 22) 6si{n}^2\mathrm{x}+7sin \mathrm{x}-3=0 \\ (2sin x +3)(3sin x-1)=0 \\ 2sin x=-3\Rightarrow sin x=-1.5 \mathrm{مرفوضة} \\ 3\sin \mathrm{x}=1\Rightarrow \sin \mathrm{x}=\frac{1}{3}\Rightarrow \mathrm{x}\approx 19.47° \mathrm{or} \mathrm{x}\approx 160.53° \\ 23) 9co{s}^2\mathrm{x}-9cos \mathrm{x}+2=0 \\ (3cos x-1)(3cos x-2)=0 \\ 3cos x=1\Rightarrow cos x=\frac{1}{3}\Rightarrow x\approx 70.53° or x\approx 289.47° \\ 3cos x=2\Rightarrow cos x=\frac{2}{3}\Rightarrow x\approx 48.19° or x\approx 311.81° \end{gathered}$$

 

$24) ta{n}^2\mathrm{\theta }+4tan \mathrm{\theta }-12=0$

$(tan \theta +6)(tan \theta -2)=0$

$tan\theta =-6 \Rightarrow \theta \approx 260.45° or \theta \approx 279.46°$

$tan \theta =2\Rightarrow \theta \approx 63.43° or \theta \approx 243.43°$

 

25) قياسات: يرتكز سلم طوله $5 m$ على ارض افقية وحائط راسي. اذا كان اسفل السلم يبعد $1.5 m$ عن الحائط، فما ارتفاع راس السلم عن الارض؟ ما قياس الزاوية التي يصنعها السلم مع الارض؟ 

$y^2=5^2-{\left(1.5\right)}^2=22.75\Rightarrow y\approx 4.77m$

$sin\theta =\frac{4.77}{5}\Rightarrow \theta =si{n}^{-1}\left(\frac{4.77}{5}\right)\Rightarrow \theta \approx 72.55°$

$\theta$ الزاوية التي يصنعها السلم مع الارض

 

26) سارية: رصد سامر قمة سارية علم ارتفاعها عن الارض $12 m$ من نقطة على الارض تبعد $30 m$ عن قاعدة السارية. اذا كان طوا سامر $1.75 m$، فما قياس الزاوية التي ينظر فيها سامر الى قمة السارية؟ 

$tan \theta =\frac{12-1.75}{30}=\frac{10.25}{30}$

$\theta =ta{n}^{-1}\left(\frac{10.25}{30}\right)\Rightarrow \theta \approx 18.86°$

$\theta$الزاوية التي ينظر فيها سامرالى قمة السارية