حل المعادلات النسبية

حَلُّ المعادلاتِ النسبيةِ

Solving Rational Equations

فكرةُ الدرسِ :  حَلُّ معادلاتٍ نسبيةٍ.

أولًا : حَلُّ المعادلاتِ النسبيةِ بالضربِ التبادليِّ

يُطلَقُ على المعادلةِ التي تحوي مقدارًا جبريًّا نسبيًّا أوْ أكثرَ اسمُ المعادلةِ النسبيةِ (rational equation) ، ومنْ أمثلتِها:

 

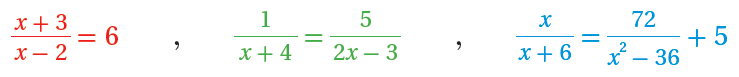
يُمكِنُ استعمالُ الضربِ التبادليِّ لحَلِّ المعادلاتِ النسبيةِ إذا كانَتْ كلٌّ منْها في صورةِ تناسبٍ فقطْ.

مثال 1 : 

أحُلُّ كلَّ معادلةٍ ممّا يأتي:

$\mathbf{1}\mathbf{)} \frac{8}{x+2}=\frac{5}{x-1}$                                                 $\mathbf{2}\mathbf{)} \frac{x-3}{2} = \frac{9}{x}$

الحل : 

$\mathbf{1}\mathbf{)} \frac{8}{x+2}=\frac{5}{x-1}$

المعادلةُ الأصليةُ	$\frac{8}{x+2}=\frac{5}{x-1}$
بالضربِ التبادليِّ	$5(x+2) = 8(x-1)$
باستعمالِ خاصيةِ التوزيعِ	$5x + 10 = 8x -8$
بالتبسيطِ	$-3x = -18$
بقسمةِ طرفيِ المعادلةِ على 3-	$x = 6$

 

أتحقَّقُ: للتحقُّقِ منْ صحَّةِ الحَلِّ، أُعوِّضُ قيمةَ x الناتجةَ في المعادلةِ الأصليةِ.

المعادلةُ الأصليةُ	$\frac{8}{x+2}=\frac{5}{x-1}$
تعويض x = 6	$\frac{8}{6+2}\stackrel{?}{=}\frac{5}{6-1}$
بالتبسيطِ	$1 = 1 ✓$

 

---

$\mathbf{2}\mathbf{)} \frac{x-3}{2}= \frac{9}{x}$

المعادلةُ الأصليةُ	$\frac{x-3}{2}= \frac{9}{x}$
بالضربِ التبادليِّ	$x(x-3) = 18$
باستعمالِ خاصيةِ التوزيعِ	$x^2 - 3x = 18$
بطرحِ 18 منْ طرفيِ المعادلةِ	$x^2 - 3x-18 = 0$
بالتحليلِ إلى العواملِ	$(x-6)(x+3) = 0$
خاصيةُ الضربِ الصفريِّ	$x-6 = 0 or x+3 = 0$
بحَلِّ كلِّ معادلةٍ	$x = 6 or x = -3$

 

أتحقَّقُ: للتحقُّقِ منْ صحَّةِ الحَلِّ، أُعوِّضُ قيمتيْ x الناتجتينِ في المعادلةِ الأصليةِ.

عندما x = -3	عندما x = 6
$\frac{x-3}{2}= \frac{9}{x}$	$\frac{x-3}{2}= \frac{9}{x}$
$\frac{-3-3}{2}\stackrel{?}{=} \frac{9}{-3}$	$\frac{6-3}{2}\stackrel{?}{=} \frac{9}{6}$
$-3 = -3 ✓$	$\frac{3}{2} = \frac{3}{2} ✓$

 

---

 

 

ثانيًا : حَلُّ المعادلاتِ النسبيةِ باستعمالِ المضاعفِ المشتركِ الأصغرِ 

يُمكن حل المعادلةَ النسبيةَ التي لا تكونُ في صورةِ تناسبٍ، وذلكَ بضربِ طرفيْ هذهِ المعادلةِ في المضاعفِ المشتركِ

الأصغرِ للمقاماتِ؛ تخلُّصًا منْ هذهِ المقاماتِ.
 

•• في بعضِ الأحيانِ ، تظهرُ حلولٌ دخيلةٌ عندَ ضربِ طرفيِ المعادلةِ النسبيةِ في المضاعفِ المشتركِ الأصغرِ؛ لذا يجبُ

التحقُّقُ دائمًا منْ تحقيقِ أيِّ حَلٍّ ناتجٍ للمعادلةِ الأصليةِ.

 

•• أتعلَّمُ : الحَلُّ الدخيلُ هوَ حَلٌّ لا يُحقِّقُ المعادلةَ الأصليةَ. ومنَ المُلاحَظِ في المعادلاتِ النسبيةِ أنَّ الحَلَّ الدخيلَ يجعلُ أحدَ مقاماتِ المعادلةِ صفرًا.

 

مثال 2 : 

أحُلُّ كلَّ معادلةٍ ممّا يأتي : 

                                                                        $\mathbf{2}\mathbf{)}\mathbf{ }\frac{10}{x^2-1}=\frac{3x}{x-1}-1$                                                              $\mathbf{1}\mathbf{)} \frac{2}{x+1}+\frac{1}{4}=\frac{1}{2}$

الحل : 

المعادلةُ الأصليةُ	$\frac{2}{x+1}+\frac{1}{4}=\frac{1}{2}$
بضربِ طرفيِ المعادلةِ في المضاعفِ المشتركِ الأصغرِ للمقاماتِ، وهوَ:  $4(x+1)$	$4(x+1) \times \frac{2}{x+1}+4(x+1) \times \frac{1}{4}= 4(x+1) \times \frac{1}{2}$
بالقسمةِ على العواملِ المشتركةِ	$8 +(x+1) = 2(x+1)$
بالتبسيطِ	$8 +x+1= 2x+2$
بالتبسيطِ	$x = 7$

 

أتحقَّقُ: للتحقُّقِ منْ صحَّةِ الحَلِّ، أُعوِّضُ قيمةَ x الناتجةَ في المعادلةِ الأصليةِ.

المعادلةُ الأصليةُ	$\frac{2}{x+1}+\frac{1}{4}=\frac{1}{2}$
بتعويضِ	$\frac{2}{7+1}+\frac{1}{4}\stackrel{?}{=}\frac{1}{2}$
بالتبسيطِ	$\frac{1}{2} = \frac{1}{2} ✓$

 

---

 

 

$\mathbf{2}\mathbf{)}\mathbf{ }\frac{10}{x^2-1}=\frac{3x}{x-1}-1$

 

المعادلةُ الأصليةُ	$\frac{10}{x^2-1}=\frac{3x}{x-1}-1$
بضربِ طرفيِ المعادلةِ في المضاعفِ المشتركِ الأصغرِ للمقاماتِ، وهوَ: $(x-1)(x+1)$	$(x-1)(x+1) \times \frac{10}{x^2-1}=(x-1)(x+1) \times \frac{3x}{x-1}-(x-1)(x+1) \times 1$
بالقسمةِ على العواملِ المشتركةِ	$10 = 3x(x+1) =(x-1)(x+1)$
بالتبسيطِ	$10 = 3x^2+3x = x^2-1$
بالتبسيطِ	$2x^2 +3x -9 = 0$
بالتحليلِ إلى العواملِ	$(2x-3)(x+3) = 0$
خاصيةُ الضربِ الصفريِّ	$(2x-3) = 0 or (x+3) = 0$
بحَلِّ كلِّ معادلةٍ	$x = \frac{3}{2} or x = -3$

 

أتحقَّقُ: للتحقُّقِ منْ صحَّةِ الحَلِّ، أُعوِّضُ قيمةَ x الناتجةَ في المعادلةِ الأصليةِ.

عندما $x = 1.5$	عندما $x = -3$
$\frac{10}{x^2-1}=\frac{3x}{x-1}-1$	$\frac{10}{x^2-1}=\frac{3x}{x-1}-1$
$\frac{10}{{(1.5)}^2-1}\stackrel{?}{=}\frac{3(1.5)}{1.5-1}-1$	$\frac{10}{{(-3)}^2-1}\stackrel{?}{=}\frac{3(-3)}{-3-1}-1$
$8 = 8 ✓$	$1.25 = 1.25 ✓$

 

•• تتطلَّبُ تطبيقاتٌ حياتيةٌ عِدَّةٌ تحديدَ الزمنِ اللازمِ لإنجازِ عملٍ مُعيَّنٍ؛ ما يُحتِّمُ تحديدَ مُعدَّلِ إنجازِ العملِ، ثمَّ استعمالَ

مُعدَّلِ الوحدةِ لكتابةِ معادلةٍ نسبيةٍ ثمَّ حَلِّها.

مثال 3 : 

تستغرقُ تنظيفُ حديقة المنزل منْ سامي وأخيه خالد ساعتان منَ العملِ. إذا كانَتْ سرعةُ سامي هيَ مثليْ سرعةِ  خالد في

التنظيفِ، فأجدُ الوقتَ الذي يستغرقُهُ سامي في تنظيفِ المنزلِ وحده.

الحل : 

الخطوةُ 1 : أُحدِّدُ مُعدَّلَ إنجازِ العملِ لكلٍّ منْ سامي وخالد
 

· أفترضُ أنَّ x هوَ عددُ الساعاتِ التي يستغرقُها خالد في تنظيفِ الحديقة وحدَهُ. وبما أنَّ خالد يُنظِّفُ الحديقة في x ساعةً، فإنَّهُ يُنظِّفُ $\frac{1}{x}$ منَ الحديقة في الساعةِ الواحدةِ.
بما أنَّ سرعةَ سامي هيَ مثلا سرعةِ خالد، فإنَّه يُنظِّفُ $\frac{2}{x}$ من الحديقة في الساعة الواحدة .
 بما أنّ سامي وخالد يُنظِّفانِ الحديقة في ساعتين إذا عملا معًا، فإنَّهُما يُنظفان $\frac{1}{2}$ الحديقة في الساعة الواحدة.  

الخطوةُ 2 : أكتبُ معادلةً تُمثِّلُ مُعدَّلَ إنجازِهِما العملَ معًا، ثمَّ أحُلُّها.

المعادلةُ الأصليةُ	$\frac{1}{x}+\frac{ 2}{x} = \frac{1}{2}$
بضربِ طرفيِ المعادلةِ في المضاعفِ المشتركِ الأصغرِ للمقاماتِ، وهوَ: 2x	$2x\times \frac{3}{x}=2x\times \frac{1}{2}$
بالقسمةِ على العواملِ المشتركةِ	$x= 6$

 

وبذلكَ، فإنَّ خالد بحاجةٍ إلى 6 ساعات منَ العملِ لتنظيفِ الحديقة.
بما أنَّ سرعةَ سامي في التنظيفِ هيَ مثلا سرعةِ خالد  فإنّه بحاجةٍ إلى3 ساعاتٍ منَ العملِ لتنظيفِالحديقة وحده.