حَلُّ المعادلاتِ النسبيةِ
أولًا : حَلُّ المعادلاتِ النسبيةِ بالضربِ التبادليِّ
يُطلَقُ على المعادلةِ التي تحوي مقدارًا جبريًّا نسبيًّا أوْ أكثرَ اسمُ المعادلةِ النسبيةِ (rational equation) ، ومنْ أمثلتِها:
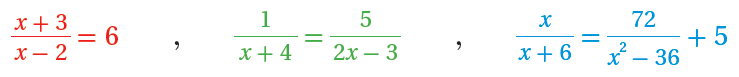
يُمكِنُ استعمالُ الضربِ التبادليِّ لحَلِّ المعادلاتِ النسبيةِ إذا كانَتْ كلٌّ منْها في صورةِ تناسبٍ فقطْ.
ثانيًا : حَلُّ المعادلاتِ النسبيةِ باستعمالِ المضاعفِ المشتركِ الأصغرِ
يُمكن حل المعادلةَ النسبيةَ التي لا تكونُ في صورةِ تناسبٍ، وذلكَ بضربِ طرفيْ هذهِ المعادلةِ في المضاعفِ المشتركِ
الأصغرِ للمقاماتِ؛ تخلُّصًا منْ هذهِ المقاماتِ.
•• في بعضِ الأحيانِ ، تظهرُ حلولٌ دخيلةٌ عندَ ضربِ طرفيِ المعادلةِ النسبيةِ في المضاعفِ المشتركِ الأصغرِ؛ لذا يجبُ
التحقُّقُ دائمًا منْ تحقيقِ أيِّ حَلٍّ ناتجٍ للمعادلةِ الأصليةِ.
|
•• أتعلَّمُ : الحَلُّ الدخيلُ هوَ حَلٌّ لا يُحقِّقُ المعادلةَ الأصليةَ. ومنَ المُلاحَظِ في المعادلاتِ النسبيةِ أنَّ الحَلَّ الدخيلَ يجعلُ أحدَ مقاماتِ المعادلةِ صفرًا. |