حل المعادلات النسبية - حل اسئلة الدرس - الصف التاسع - رياضيات فصل ثاني - مدرسة جواكاديمي

حلول أسئلة كتاب الطالب وكتاب التمارين

أسئلة أتحقق من فهمي

أتحقق من فهمي صفحة 109

أحُلُّ كلَّ معادلةٍ ممّا يأتي:

الحل :

يجب التحقق من صحة الحل ، وذلك بتعويض قيم x في المعادلة الأصلية .

$a) \frac{4}{x} = \frac{3}{x - 2}$

$\frac{4}{x} = \frac{3}{x - 2} 3 x = 4 (x - 2) 3 x = 4 x - 8 x = 8$

$b) \frac{4}{x + 4} = \frac{x}{x + 1}$

$\frac{4}{x + 4} = \frac{x}{x + 1} x (x + 4) = 4 (x + 1) x^{2} + 4 x = 4 x + 4 x^{2} - 4 = 0 (x - 2) (x + 2) = 0 x = 2 o r x = - 2$

أتحقق من فهمي صفحة 111

طلاءٌ : وُضِعَ في خلاّطِ متجرٍ للطلاءِ مكيالٌ منَ اللونِ الأحمرِ و 4 مكاييلَ منَ اللونِ الأصفرِ لإنتاجِ لونٍ

مُعيَّنٍ. إذا كانَتْ درجةُ هذا اللونِ مشروطةً بأنْ تكونَ نسبةُ اللونِ الأحمرِ إلى الخليطِ هيَ 3 : 1، فأجدُ عددَ

مكاييلِ اللونِ الأحمرِ التي يتعيَّنُ إضافتُها إلى الخليطِ للحصولِ على الدرجةِ المطلوبةِ منَ اللونِ.

الحل :

أفترضُ أنَّ x هوَ عددُ مكاييلِ اللونِ الأحمرالتي يجبُ إضافتُها إلى الخليطِ لإيجادِ النسبةِ المطلوبةِ.
$\frac{x + 1}{x + 5} = \frac{1}{3} 3 x + 3 = x + 5 2 x = 2 x = 1$

أتحقق من فهمي صفحة 113

أحُلُّ كلَّ معادلةٍ ممّا يأتي:

الحل :

$a) \frac{1}{x - 1} + \frac{1}{2} = \frac{5}{8}$

$8 (x - 1) \times \frac{1}{x - 1} + 8 (x - 1) \times \frac{1}{2} = 8 (x - 1) \times \frac{5}{8} 8 + 4 (x - 1) = 5 (x - 1) 8 + 4 x - 4 = 5 x - 5 x = 9$

$b) = \frac{x}{x - 2} + \frac{1}{3 x - 1} = \frac{x}{3 x^{2} - 7 x + 2}$

$(x - 2) (3 x - 1) \times \frac{x}{x - 2} + (x - 2) (3 x - 1) \times \frac{1}{3 x - 1} = (x - 2) (3 x - 1) \times \frac{x}{(x - 2) (3 x - 1)} x (3 x - 1) + (x - 2) = x 3 x^{2} - x + x - 2 - x = 0 3 x^{2} - x - 2 = 0 (3 x + 2) (x - 1) = 0 x = - \frac{2}{3} o r x = 1$

أتحقق من فهمي صفحة 114

جدارٌ : يتعيَّنُ على يوسفَ وإبراهيمَ العملُ 6 ساعاتٍ لطلاءِ جدارٍ في حديقةٍ منزليةٍ. إذا كانَتْ سرعةُ يوسفَ هيَ ثلاثةَ أمثالِ

سرعةِ إبراهيمَ في إنجازِ العملِ، فأجدُ الوقتَ الذي يستغرقُهُ يوسفُ في طلاءِ الجدارِ وحدَهُ.

الحل :

الخطوةُ 1 : أُحدِّدُ مُعدَّلَ إنجازِ العملِ لكلٍّ منْ يوسف وإبراهيم

· أفترضُ أنَّ x هوَ عددُ الساعاتِ التي يستغرقُها إبراهيم في طلاء الجدار وحدَهُ. وبما أنَّ إبراهيم يطلي الجدار في x ساعةً، فإنَّهُ يطلي $\frac{1}{x}$ منَ الجدار في الساعةِ الواحدة

بما أنَّ سرعةَ يوسف هيَ ثلاثة أمثال سرعةِ خالد، فإنَّه يطلي $\frac{3}{x}$ من الجدار في الساعة الواحدة .

بما أنّه يتعين على يوسف وإبراهيم طلاء الجدار في 6 ساعات إذا عملا معاً ، فإنَّهُما يقومان بطلي $\frac{1}{6}$ الجدار في الساعة الواحدة.

الخطوةُ 2 : أكتبُ معادلةً تُمثِّلُ مُعدَّلَ إنجازِهِما العملَ معًا، ثمَّ أحُلُّها.

المعادلةُ الأصليةُ	$\frac{1}{x} + \frac{3}{x} = \frac{1}{6}$
بضربِ طرفيِ المعادلةِ في المضاعفِ المشتركِ الأصغرِ للمقاماتِ، وهوَ: 6x	$6 x \times \frac{4}{x} = 6 x \times \frac{1}{6}$
بالقسمةِ على العواملِ المشتركةِ	$x = 24$

وبذلكَ، فإنَّ إبراهيم بحاجةٍ إلى 24 ساعة منَ العملِ لطلاء الجدار.
بما أنَّ سرعةَ يوسف في طلاء الجدار هيَ ثلاثة أمثال سرعةِ إبراهيم فإنّه بحاجةٍ إلى 8 ساعاتٍ منَ العملِ لطلاء الجدار وحده.

أسئلة أتدرَّبُ وأحُلُّ المسائلَ

أحُلُّ كُلًّ منَ المعادلاتِ الآتيةِ :

الحل :

ملاحظة : يجب التحقق من صحة الحل ، وذلك بتعويض قيم المتغير الناتجة في المعادلة الأصلية .

$1) \frac{3 y}{y + 1} = \frac{y}{3 - y}$

$3 y (3 - y) = y (y + 1) 9 y - 3 {y^{}}^{2} = y^{2} + y 8 y - 4 y^{2} = 0 4 y (2 - y) = 0 y = 0 o r y = 2$

$2) \frac{2}{x + 5} = \frac{10}{3 x + 7}$

$10 (x + 5) = 2 (3 x + 7) 10 x + 50 = 6 x + 14 4 x = - 36 x = - 9$

$3) \frac{6}{y - 1} = \frac{y}{7}$

$y (y - 1) = 6 \times 7 y^{2} - y = 42 y^{2} - y - 42 = 0 (y - 7) (y + 6) = 0 y = 7 o r y = - 6$

$4) \frac{9}{y - 1} = \frac{3 y}{2}$

$3 y (y - 1) = 9 \times 2 3 y^{2} - 3 y = 18 3 y^{2} - 3 y - 18 = 0 y^{2} - y - 6 = 0 (y - 3) (y + 2) = 0 y = 3 o r y = - 2$

$5) \frac{w}{w + 1} = \frac{2 w}{w + 6}$

$2 w (w + 1) = w (w + 6) 2 w^{2} + 2 w = w^{2} + 6 w w^{2} - 4 w = 0 w (w - 4) = 0 w = 0 o r w = 4$

$6) = \frac{x^{2} + 4}{x - 1} = \frac{5}{x - 1}$

$(x^{2} + 4) (x - 1) = 5 (x - 1) x^{2} + 4 = 5 x^{2} = 1 x = 1 o r x = - 1$

بعد التحقق بتعويض قيم x في المعادلة الأصلية ، فإنّ x = - 1 تحقق المعادلة .

7 ) أشجارٌ : تحتوي مزرعةٌ للحمضياتِ على 120 شجرةً، منْها 30 شجرةَ ليمونٍ.

أجدُ عددَ أشجارِ الليمونِ التي يَلزمُ زراعتُها لتُصبِحَ نسبةُ أشجارِ الليمونِ في المزرعةِ 3 : 1.

الحل :

أفرض عدد أشجار الليمون هو x

$\frac{x + 30}{x + 120} = \frac{1}{3} 3 (x + 30) = x + 120 3 x + 90 = x + 120 2 x = 30 x = 15$

أحُلُّ كُلًّ منَ المعادلاتِ الآتيةِ:

الحل :

$8) \frac{4}{y} + \frac{3}{8} = \frac{6}{y}$

$8 y \times \frac{4}{y} + 8 y \times \frac{3}{8} = 8 y \times \frac{6}{y} 32 + 3 y = 48 3 y = 16 y = \frac{16}{3}$

$9) \frac{4}{y - 2} - 1 = \frac{9}{y}$

$y (y - 2) \times \frac{4}{y - 2} - y (y - 2) \times 1 = y (y - 2) \times \frac{9}{y} 4 y - y^{2} + 2 y = 9 y - 18 y^{2} + 3 y - 18 = 0 (y - 6) (y + 3) = 0 y = 6 o r y = - 3$

$10) \frac{1}{z} + \frac{1}{z - 4} = \frac{z - 3}{z - 4}$

$z (z - 4) \times \frac{1}{z} + z (z - 4) \times \frac{1}{z - 4} = z (z - 4) \times \frac{z - 3}{z - 4} z - 4 + z = z (z - 3) 2 z - 4 = z^{2} - 3 z z^{2} - 5 z + 4 = 0 (z - 1) (z - 4) = 0 z = 1 o r z = 4$

بعد التحقق بتعويض قيم z في المعادلة الأصلية ، فإنّ z = 1 تحقق المعادلة .

$11) \frac{3}{x - 2} + \frac{2 x}{x + 2} = \frac{3 x^{2}}{x^{2} - 4}$

$(x - 2) (x + 2) \times \frac{3}{x - 2} + (x - 2) (x + 2) \times \frac{2 x}{x + 2} = (x - 2) (x + 2) \times \frac{3 x^{2}}{(x - 2) (x + 2)} 3 (x + 2) + 2 x (x - 2) = 3 x^{2} 3 x + 6 + 2 x^{2} - 4 x = 3 x^{2} x 2 + x - 6 = 0 (x - 2) (x + 3) = 0 x = 2 o r x = - 3$

بعد التحقق بتعويض قيم x في المعادلة الأصلية ، فإنّ x = -3 تحقق المعادلة .

$12) \frac{x^{2} - 3 x - 4}{x^{3} - x^{2}} - \frac{1}{x^{2}} = \frac{x - 2}{x^{2}}$

$x^{2} (x - 1) \times \frac{x^{2} - 3 x - 4}{x^{2} (x - 1)} - x^{2} (x - 1) \times \frac{1}{x^{2}} = x^{2} (x - 1) \times \frac{x - 2}{x^{2}} x^{2} - 3 x - 4 - (x - 1) = (x - 1) (x - 2) x^{2} - 3 x - 4 - x + 1 = x^{2} - 3 x + 2 - x - 3 = 2 x = - 5$

$13) 10 + \frac{14}{1 - x} = \frac{12}{1 - x^{2}}$

$(1 - x) (1 + x) \times 10 + (1 - x) (1 + x) \times \frac{14}{1 - x} = (1 - x) (1 + x) \times \frac{12}{(1 - x) (1 + x)} 10 - 10 x^{2} + 14 (1 + x) = 12 10 - 10 x^{2} + 14 + 14 x = 12 10 x^{2} - 14 x - 12 = 0 5 x^{2} - 7 x - 6 = 0 (5 x + 3) (x - 2) = 0 x = - \frac{3}{5} o r x = 2$

$14) \frac{1}{x + 5} - \frac{1}{x^{2} + 5 x} = \frac{4}{x^{2} + 5 x}$

$x (x + 5) \times \frac{1}{x + 5} - x (x + 5) \times \frac{1}{x (x + 5)} = x (x + 5) \times \frac{4}{x (x + 5)} x - 1 = 4 x = 5$

$15) 1 = \frac{n - 2}{n - 1} + \frac{3}{n^{2} + 3 n - 4}$

$(n - 1) (n + 4) \times 1 = (n - 1) (n + 4) \times \frac{n - 2}{n - 1} + (n - 1) (n + 4) \times \frac{3}{(n - 1) (n + 4)} n^{2} + 3 n - 4 = (n + 4) (n - 2) + 3 n^{2} + 3 n - 4 = n^{2} + 2 n - 8 + 3 n - 4 = - 5 n = - 1$

$16) \frac{16}{x - 5} = 2 - \frac{6}{x}$

$x (x - 5) \times \frac{16}{x - 5} = x (x - 5) \times 2 - x (x - 5) \times \frac{6}{x} 16 x = 2 x^{2} - 10 x - 6 x + 30 2 x^{2} - 32 x + 30 = 0 x^{2} - 16 x + 15 = 0 (x - 1) (x - 15) = 0 x = 1 o r x = 15$

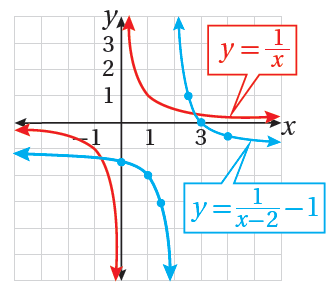
يُبيِّنُ الشكلُ المُجاوِرُ التمثيلَ البيانيَّ لمنحنى كلٍّ منَ المعادلةِ : $y = \frac{1}{x}$

والمعادلةِ : $y = \frac{1}{x - 2} - 1$

17) أكتبُ معادلةً حَلُّها هوَ الإحداثيُّ x لنقطةِ تقاطعِ منحنييِ المعادلتينِ.

18) أحُلُّ المعادلةَ التي كتبْتُها في الفرعِ السابقِ جبريًّا.

الحل :

17)

$\frac{1}{x} = \frac{1}{x - 2} - 1$

18)

$\frac{1}{x} = \frac{1}{x - 2} - 1 x (x - 2) \times \frac{1}{x} = x (x - 2) \times \frac{1}{x - 2} - x (x - 2) \times 1 x - 2 = x - x^{2} + 2 x x^{2} - 2 x - 2 = 0$

أحل المعادلة الناتجة باستخدام القانون العام لحل المعادلة التربيعية

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} x = \frac{- (- 2) \pm \sqrt{{(- 2)}^{2} - 4 (1) (- 2)}}{2 (1)} x = \frac{2 \pm \sqrt{12}}{2} x = \frac{2 + \sqrt{12}}{2} o r x = \frac{2 - \sqrt{12}}{2}$

19) مسبحٌ: يستغرقُ مِلْءُ مسبحٍ بالماءِ 45 دقيقةً باستعمالِ خرطومِ المياهِ الأزرقِ، في

حينِ يستغرقُ مِلْئُهُ بالماءِ 20 دقيقةً باستعمالِ هذا الخرطوم وخرطومِ المياهِ ذي اللونِ

الأسودِ معًا. أجدُ عددَ الدقائقِ التي يستغرقُها الخرطومُ الأسودُ في مِلْءِ المسبحِ بالماءِ.

الحل :

أُحدِّدُ مُعدَّلَ إنجازِ العملِ لكلٍّ منْ الخرطوم الأسود والخرطوم الأزرق .

ثمّ أكتبُ معادلةً تُمثِّلُ مُعدَّلَ إنجازِهِما العملَ معًا، ثمَّ أحُلُّها.

أفرض عدد الدقائق التي يستغرقها الخرطوم الأسود هو x

$\frac{1}{x} + \frac{1}{45} = \frac{1}{20} 180 x \times \frac{1}{x} + 180 x \times \frac{1}{45} = 180 x \times \frac{1}{20} 180 + 4 x = 9 x 5 x = 180 x = 36$

20) أحُلُّ المسألةَ الواردةَ بدايةَ الدرسِ.

مسألةُ اليومِ : يُنتِجُ مصنعٌ سبائكَ منَ النحاسِ والفِضَّةِ، نسبةُ الفِضَّةِ فيها هيَ 5 : 2.

كمْ غرامًا منَ الفِضَّةِ يجبُ إضافتُها إلى خليطٍ منَ النحاسِ والفِضَّةِ، كتلتُهُ 800 g ، ومقدارُ الفِضَّةِ

فيهِ 200 g ؛ لكيْ تكونَ النسبةُ اللازمةُ لصنعِ السبيكةِ هيَ 5 : 2؟

الحل :

أفرض عدد غرامات الفضة = x

$\frac{x + 200}{x + 800} = \frac{2}{5} 2 (x + 800) = 5 (x + 200) 2 x + 1600 = 5 x + 1000 3 x = 600 x = 200$

مهاراتُ التفكيرِ العليا

21) مسألةٌ مفتوحةٌ : أكتبُ معادلةً نسبيةً يُمكِنُ حَلُّها بضربِ طرفيِ المعادلةِ في (x – 1)3.

الحل :

$\frac{x}{x - 1} + 1 = \frac{2}{3}$

22) أكتشفُ الخطأَ : يُمثِّلُ التالي الخطوةَ الأولى منَ حَلِّ ديمةَ لمعادلةٍ نسبيةٍ. أكتشفُ الخطأَ في هذهِ الخطوةِ، ثمَّ أُصحِّحُهُ.

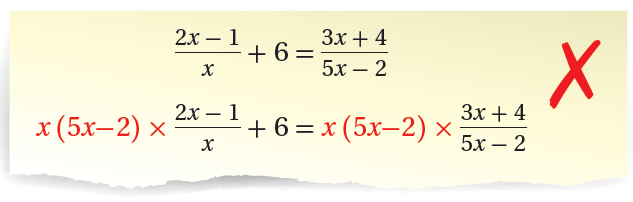
الإجابة :

لم يتم ضرب 6 في المضاعف المشترك الأصغر

الحل الصحيح :

$\frac{2 x - 1}{x} + 6 = \frac{3 x + 4}{5 x - 2} x (5 x - 2) \times \frac{2 x - 1}{x} + x (5 x - 2) \times 6 = x (5 x - 2) \times \frac{3 x + 4}{5 x - 2}$

23) تبريرٌ : هلْ يُمكِنُ حَلُّ المعادلةِ : $\frac{6 x}{x + 4} + 4 = \frac{2 x + 2}{x - 1}$ باستعمالِ الضربِ التبادليِّ؟ أُبرِّرُ إجابتي.

الإجابة :

يُمكن ذلك إذا تم إجراء عملية الجمع في الطرف الأيسر من المعادلة ثم حل المعادلة بالضرب التبادلي .

24) تحدٍّ : أحُلُّ المعادلةَ الآتيةَ : $\frac{\frac{x + 3}{x - 2} \times \frac{x^{2} + x - 2}{x + 5}}{x - 1} + 2 = 0$

الحل :

$\frac{\frac{x + 3}{x - 2} \times \frac{x^{2} + x - 2}{x + 5}}{x - 1} + 2 = 0 \frac{(x + 3) (x + 2) (x - 1)}{(x - 2) (x + 5)} \div (x - 1) + 2 = 0 \frac{(x + 3) (x + 2) (x - 1)}{(x - 2) (x + 5)} \times \frac{1}{(x - 1)} + 2 = 0 \frac{(x + 3) (x + 2)}{(x - 2) (x + 5)} + 2 = 0 (x - 2) (x + 5) \times \frac{(x + 3) (x + 2)}{(x - 2) (x + 5)} + (x - 2) (x + 5) \times 2 = (x - 2) (x + 5) \times 0 (x + 3) (x + 2) + 2 (x - 2) (x + 5) = 0$

$x^{2} + 5 x + 6 + 2 x^{2} + 6 x - 20 = 0 3 x 2 + 11 x - 14 = 0 (3 x + 14) (x - 1) = 0 3 x + 14 = 0 \Rightarrow x = - \frac{14}{3} o r x = 1$

x = 1 يجعل المقام يساوي صفر

أسئلة كتاب التمارين

أحُلُّ كُلًّ منَ المعادلاتِ الآتيةِ :

الحل :

$1) \frac{12}{x - 1} + \frac{3}{2} = \frac{9}{2}$

$2 (x - 1) \times \frac{12}{x - 1} + 2 (x - 1) \times \frac{3}{2} = 2 (x - 1) \times \frac{9}{2} 24 + 3 x - 3 = 9 x - 9 6 x = 30 x = 5$

$2) \frac{x}{1 - x} - \frac{4}{3} = x$

$3 (1 - x) \times \frac{x}{1 - x} - 3 (1 - x) \times \frac{4}{3} = 3 (1 - x) \times x 3 x - 4 + 4 x = 3 x - 3 x^{2} 3 x^{2} + 4 x - 4 = 0 (x + 2) (3 x - 2) = 0 x = - 2 o r x = \frac{2}{3}$

$3) \frac{4}{x + 1} + 1 = \frac{x + 1}{2}$

$2 (x + 1) \times \frac{4}{x + 1} + 2 (x + 1) \times 1 = 2 (x + 1) \times \frac{x + 1}{2} 8 + 2 x + 2 = x^{2} + 2 x + 1 x^{2} - 9 = 0 x = 3 o r x = - 3$

$4) \frac{y + 9}{y^{2} + 3} = \frac{3}{y}$

$3 y^{2} + 9 = y^{2} + 9 y 2 y^{2} - 9 y + 9 = 0 (2 y - 3) (y - 3) = 0 y = \frac{3}{2} o r y = 3$

$5) \frac{w}{w + 2} = \frac{5 w - 4}{2 w + 1}$

$(5 w - 4) (w + 2) = w (2 w + 1) 5 w^{2} + 6 w - 8 = 2 w^{2} + w 3 w^{2} + 5 w - 8 = 0 (w - 1) (3 w + 8) = 0 w = 1 o r w = - \frac{8}{3}$

$6) \frac{1}{y - 3} + \frac{1}{y + 3} = \frac{3}{y^{2} - 9}$

$(y - 3) (y + 3) \times \frac{1}{y - 3} + (y - 3) (y + 3) \times \frac{1}{y + 3} = (y - 3) (y + 3) \times \frac{3}{(y - 3) (y + 3)} y + 3 + y - 3 = 3 2 y = 3 y = \frac{3}{2}$

$7) \frac{1}{b - 4} + \frac{b}{2 b + 2} = \frac{b}{2 b^{2} - 6 b - 8}$

$\frac{1}{b - 4} + \frac{b}{2 (b + 1)} = \frac{b}{2 (b - 4) (b + 1)} 2 (b - 4) (b + 1) \times \frac{1}{b - 4} + 2 (b - 4) (b + 1) \times \frac{b}{2 (b + 1)} = 2 (b - 4) (b + 1) \times \frac{b}{2 (b - 4) (b + 1)} 2 b + 2 + b^{2} - 4 b = b b^{2} - 3 b + 2 = 0 (b - 2) (b - 1) = 0 b = 2 o r b = 1$

$8) \frac{1}{x + 1} - \frac{x}{1 - x} = \frac{x^{2} + 1}{x^{2} - 1}$

$- (x - 1) (x + 1) \times \frac{1}{x + 1} - - (x - 1) (x + 1) \times \frac{x}{1 - x} = - (x - 1) (x + 1) \times \frac{x^{2} + 1}{(x - 1) (x + 1)} - x + 1 - x^{2} - x = - x^{2} - 1 - 2 x = - 2 x = 1$

بعد التحقق من صحة الحل فإنّ x = 1 تجعل المقام يساوي صفر ، إذن لا يوجد حلول لهذه المعادلة .

$9) \frac{1}{2 c + 1} + \frac{2}{c + 2} = 1$

$(2 c + 1) (c + 2) \times \frac{1}{2 c + 1} + (2 c + 1) (c + 2) \times \frac{2}{c + 2} = (2 c + 1) (c + 2) \times 1 c + 2 + 4 c + 2 = 2 c^{2} + 5 c + 2 5 c + 4 = 2 c^{2} + 5 c + 2 2 c^{2} - 2 = 0 2 (c^{2} - 1) = 0 c = 1 o r c = - 1$

10) حيواناتٌ : يوجدُ في مزرعةٍ للحيواناتِ 140 حيوانًا، منْها 10 أرانبَ. أجدُ عددَ الأرانبِ التي يَلزمُ شراؤُها لتُصبِحَ نسبةُ

الأرانبِ في المزرعةِ 6 : 1

الحل :

أفرض عدد الأرانب اللازم شراؤها هو x

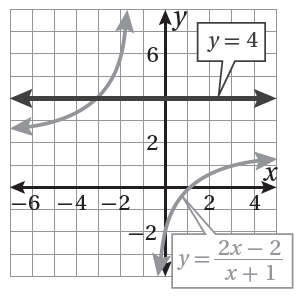
$\frac{x + 10}{x + 140} = \frac{1}{6} 6 x + 60 = x + 140 5 x = 80 x = 16$

يُبيِّنُ الشكلُ المُجاوِرُ التمثيلَ البيانيَّ لمنحنى كلٍّ منَ المعادلةِ : $y = 4$
والمعادلةِ : $y = \frac{2 x - 2}{x + 1}$

11) أكتبُ معادلةً حَلُّها هوَ الإحداثيُّ x لنقطةِ تقاطعِ منحنييِ المعادلتينِ.

12) أحُلُّ المعادلةَ التي كتبْتُها في الفرعِ السابقِ جبريًّا.

الحل :

11)

$\frac{2 x - 2}{x + 1} = 4$

12)

$\frac{2 x - 2}{x + 1} = 4 4 x + 4 = 2 x - 2 2 x = - 6 x = - 3$

13) تبليطٌ: يستغرقُ تبليطُ حديقةِ منزلٍ منْ خالدٍ وسعيدٍ 8 ساعاتٍ منَ العملِ. إذا كانَتْ سرعةُ خالدٍ هيَ ثلاثةَ أمثالِ سرعةِ

سعيدٍ في التبليطِ، فأجدُ الوقتَ الذي يستغرقُهُ خالدٌ في تبليطِ حديقةِ المنزلِ وحدَهُ.

الحل :

أُحدِّدُ مُعدَّلَ إنجازِ العملِ لكلٍّ منْ خالد وسعيد.
أفترضُ أنَّ x هوَ عددُ الساعاتِ التي يستغرقُها سعيد في تبليط حديقة المنزلِ وحدَهُ.

$\frac{1}{x} + \frac{3}{x} = \frac{1}{8} \frac{4}{x} = \frac{1}{8} x = 32$

وبذلكَ، فإنَّ سعيد بحاجةٍ إلى 32 ساعةً منَ العملِ لتبليط حديقة المنزلِ وحده.
بما أنَّ سرعةَ خالد في التبليط هيَ ثلاثة أمثال سرعةِ سعيد ، فإنَّه بحاجةٍ إلى $\frac{32}{3} \approx 11$ ساعاتٍ منَ العملِ
لتبليط حديقة المنزلِ وحدَه.

رياضيات فصل ثاني

التاسع

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS