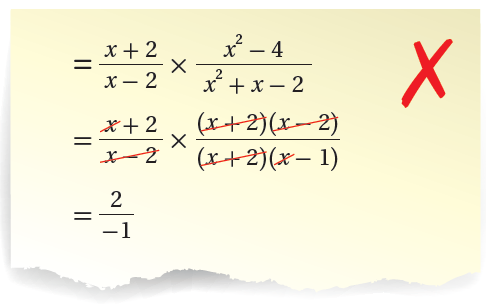رياضيات 9 فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من قهمي صفحة 94

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ:

الحل: 

$\mathit{a}\mathbf{)} \frac{6x-18}{x^4-81}$

بتحليلِ كلٍّ منَ البسطِ والمقامِ إلى العواملِ	$\frac{6x-18}{x^4-81}= \frac{6(x - 3)}{(x^2-9)(x^2+9)}$
بتحليل المقام	$= \frac{6(x - 3)}{(x-3)(x+3)(x^2+9)}$
بقسمةِ كلٍّ منَ البسطِ والمقامِ على العوامل المشتركة	$= \frac{6\cancel{(x - 3)}}{\cancel{(x-3)}(x+3)(x^2+9)}$
بالتبسيط	$=\frac{6}{(x+3)(x^2+9)}$

 

---

 

$\mathit{b}\mathbf{)}\mathbf{ }\frac{x^3+8}{x^2+6x +8}$

بتحليلِ كلٍّ منَ البسطِ والمقامِ إلى العواملِ	$\frac{x^3+8}{x^2+6x +8}=\frac{(x+2)(x^2-2x+4)}{(x+2)(x+4)}$
بقسمةِ كلٍّ منَ البسطِ والمقامِ على العوامل المشتركة	$=\frac{\cancel{(x+2)}(x^2-2x+4)}{\cancel{(x+2)}(x+4)}$
بالتبسيط	$= \frac{x^2-2x+4}{x+4}$

 

---

 

$\mathit{c}\mathbf{)} \frac{3x-3x^2}{x^2+4x-5}$

بتحليلِ كلٍّ منَ البسطِ والمقامِ إلى العواملِ	$\frac{3x-3x^2}{x^2+4x-5}= \frac{3x(1-x)}{(x-1)(x+5)}$
بإخراج 1- كعامل مشترك من (1 - x)في المقام	$=\frac{3x(1-x)}{-(1-x)(x+5)}$
بقسمةِ كلٍّ منَ البسطِ والمقامِ على العوامل المشتركة	$=\frac{3x\cancel{(1-x)}}{-\cancel{(1-x)}(x+5)}$
بالتبسيط	$=\frac{3x}{-(x+5)}$

 

 

---

 

 

أتحقق من قهمي صفحة 95

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ:

$\mathit{a}\mathbf{)} \frac{8x}{5y^2} \times \frac{20xy}{6b} \mathit{b}\mathbf{)} \frac{d^2-36}{d^2+5d-6} \times \frac{d-1}{ d^2-7d+6}$

الحل : 

$\mathit{a}\mathbf{)} \frac{8x}{5y^2} \times \frac{20xy}{6b}$

بتحليلِ كلٍّ منَ البسطِ والمقامِ إلى العواملِ	$\frac{8x}{5y^2} \times \frac{20xy}{6b} =\frac{2\times 4\times x\times 5\times 4\times x\times y}{5\times y\times y\times 2\times 3\times b}$
بقسمةِ كلٍّ منَ البسطِ والمقامِ على العوامل المشتركة	$=\frac{\cancel{2}\times 4\times x\times \cancel{5}\times 4\times x\times \cancel{y}}{\cancel{5}\times \cancel{y}\times y\times \cancel{2}\times 3\times b}$
بالتبسيط	$=\frac{16x^2}{3yb}$

 

---

 

$\mathit{b}\mathbf{)} \frac{d^2-36}{d^2+5d-6} \times \frac{d-1}{ d^2-7d+6}$

 

بتحليلِ كلٍّ منَ البسطِ والمقامِ إلى العواملِ	$\frac{d^2-36}{d^2+5d-6} \times \frac{d-1}{ d^2-7d+6}=\frac{(d-6)(d+6)}{(d+6)(d-1)}\times \frac{d-1}{(d-6)(d-1)}$
بقسمةِ كلٍّ منَ البسطِ والمقامِ على العوامل المشتركة	$=\frac{\cancel{(d-6)}\cancel{(d+6)}}{\cancel{(d+6)}\cancel{(d-1)}}\times \frac{\cancel{d-1}}{\cancel{(d-6)}(d-1)}$
بالتبسيط	$= \frac{1}{d-1}$

 

---

 

أتحقق من قهمي صفحة 96

قهوةٌ: تضعُ إحدى الشركاتِ مُنتَجَها منَ القهوةِ في علبٍ، أبعادُها تعطى بدلالةِ x كما في الشكلِ المُجاوِرِ. أجدُ حجمَ علبةِ القهوةِ بدلالةِ x في أبسطِ صورةٍ.

 

الحل : 

حجم الأسطوانة  = مساحة القاعدة $\times$ الارتفاع

أفرض حجم الأسطوانة هو A  

نصف قطر قاعدة الأسطوانة : $\frac{1}{2}\times \frac{2x-6}{x+5} = \frac{2x-6}{2(x+5)} =\frac{\cancel{2}(x-3)}{\cancel{2}(x+5)} = \frac{x-3}{x+5}$

 

أعوض في قانون حجم الأسطوانة المعطيات	$A = \mathrm{\pi } \times {\left(\frac{x-3}{x+5}\right)}^2 \times \frac{1}{{\mathrm{x}}^2+\mathrm{x}-12}$
بتحليلِ كلٍّ منَ البسطِ والمقامِ إلى العواملِ	$A = \mathrm{\pi } \times \frac{(x-3)(x-3)}{(x+5)(x+5)} \times \frac{1}{ (x+4)(x-3)}$
بقسمةِ كلٍّ منَ البسطِ والمقامِ على العوامل المشتركة	$A = \mathrm{\pi } \times \frac{(x-3)\cancel{(x-3)}}{(x+5)(x+5)} \times \frac{1}{ (x+4)\cancel{(x-3)}}$
بالتبسيط	$A =\frac{ (\mathrm{x}-3)\mathrm{\pi }}{(x+4){(x+5)}^2}$

 

---

 

أتحقق من قهمي صفحة 97

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ :

$\mathit{a}\mathbf{)} \frac{24b^3}{14x^2 y^2} ÷ \frac{16 b{c}^2}{21x^4 y^3}$

 

بضربِ المقسومِ في النظيرِ الضربيِّ للمقسومِ عليْهِ	$\frac{24b^3}{14x^2 y^2} ÷ \frac{16 b{c}^2}{21x^4 y^3} =\frac{24b^3}{14x^2 y^2}\times \frac{21x^4 y^3}{16 b{c}^2}$
بتحليلِ كلٍّ منَ البسطِ والمقامِ إلى العواملِ	$=\frac{3\times 4\times 2\times b\times b^2}{7\times 2\times x^2\times y^2}\times \frac{3\times 7\times x^2\times x^2\times y\times y^2}{4\times 4\times b\times c^2}$
بقسمةِ كلٍّ منَ البسطِ والمقامِ على العواملِ المشتركةِ	$=\frac{3\times \cancel{4}\times \cancel{2}\times \cancel{b}\times b^2}{\cancel{7}\times \cancel{2}\times \cancel{x^2}\times \cancel{y^2}}\times \frac{3\times \cancel{7}\times \cancel{x^2}\times x^2\times y\times \cancel{y^2}}{4\times \cancel{4}\times \cancel{b}\times c^2}$
بالتبسيطِ	$=\frac{9b^2{x}^{2 }y}{4c^2}$

 

$\mathit{b}\mathbf{)} \frac{x^2- 9x + 20}{y^2 + 10y + 21} ÷ \frac{2x^2 - 9x + 4}{4y + 28}$

بضربِ المقسومِ في النظيرِ الضربيِّ للمقسومِ عليْهِ	$\frac{x^2- 9x + 20}{y^2 + 10y + 21} ÷ \frac{2x^2 - 9x + 4}{4y + 28}= \frac{x^2- 9x + 20}{y^2 + 10y + 21}\times \frac{4y + 28}{2x^2 - 9x + 4}$
بتحليلِ كلٍّ منَ البسطِ والمقامِ إلى العواملِ	$= \frac{(x-4)(x-5) }{(y+7)(y+3) }\times \frac{4(y+7) }{(2x-1)(x-4) }$
بقسمةِ كلٍّ منَ البسطِ والمقامِ على العواملِ المشتركةِ	$= \frac{\cancel{(x-4)}(x-5) }{\cancel{(y+7)}(y+3) }\times \frac{4\cancel{(y+7)} }{(2x-1)\cancel{(x-4) }}$
بالتبسيطِ	$=\frac{4(x-5)}{(y+3)(2x-1)}$

 

---

 

أتحقق من قهمي صفحة 98

أكتبُ $\frac{\frac{x^2 - y^2}{y^2 - 36}}{\frac{x - y}{2y + 12}}$ في أبسطِ صورةٍ.

الحل : 

بكتابةِ الكسرِ الجبريِّ المُركَّبِ في صورةِ قسمةِ مقدارينِ نسبيينِ	$\frac{\frac{x^2 - y^2}{y^2 - 36}}{\frac{x - y}{2y + 12}}=\frac{x^2 - y^2}{y^2 - 36}÷\frac{x - y}{2y + 12}$
بضربِ المقسومِ في النظيرِ الضربيِّ للمقسومِ عليْهِ	$=\frac{x^2 - y^2}{y^2 - 36}\times \frac{2y + 12 }{ x-y}$
بالتحليل إلى العوامل	$=\frac{ (x-y)(x+y)}{ (y-6)(y+6)}\times \frac{ 2(y+6)}{ x-y}$
بقسمةِ كلٍّ منَ البسطِ والمقامِ على العواملِ المشتركةِ	$=\frac{ \cancel{(x-y)}(x+y)}{ (y-6)\cancel{(y+6)}}\times \frac{ 2\cancel{(y+6)}}{ \cancel{x-y}}$
بالتبسيطِ	$=\frac{2(x+y)}{y-6}$

 

أسئلة أتدرب وأحل المسائل 

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ:

$\mathbf{1}\mathbf{)}\mathbf{ }\frac{6x(x + 3)}{9x^2}$

$\frac{6x(x+3)}{9x^2}=\frac{2\times \cancel{3}\times \cancel{x}\times (x+3)}{\cancel{3}\times 3\times \cancel{x}\times x }=\frac{2(x+3)}{3x}$

 

$\mathbf{2}\mathbf{)} \frac{b^2 + 5b + 4}{b^2-2b -24}$

$\frac{b^2 + 5b + 4}{b^2-2b -24}=\frac{\cancel{(b+4)}(b+1)}{(b-6)\cancel{(b+4)}}= \frac{b+1}{b-6}$

 

$\mathbf{3}\mathbf{)}\mathbf{ }\frac{2x^3-18x}{6x^3-12x^2 -18x}$

$\frac{2x^3-18x}{6x^3-12x^2-18x}=\frac{2x(x^2-9)}{6x(x^2-2x-3)}= \frac{\cancel{2}\times \cancel{x}\times \cancel{(x-3)}(x+3)}{\cancel{2}\times 3\times \cancel{x}\times \cancel{(x-3)}(x+1)}=\frac{x+3}{3(x+1)}$

---

 

$\mathbf{4}\mathbf{)}\mathbf{ }\mathbf{ }\frac{x^3-8}{x^2-4}$

$\frac{x^3-8}{x^2-4}=\frac{\cancel{(x-2)}(x^2+2x+4)}{\cancel{(x-2)}(x+2)} = \frac{x^2+2x+4}{x+2}$

---

 

$\mathbf{5}\mathbf{)} \frac{x^3-9x^2}{x^2-3x-54}$

$\frac{x^3-9x^2}{x^2-3x-54}=\frac{x^2\cancel{(x-9)}}{\cancel{(x-9)}(x+6)} = \frac{x^2}{x+6}$

 

$\mathbf{6}\mathbf{)} \frac{32x^4-50}{4x^3-12x^2-5x+15}$

$\frac{32x^4-50}{4x^3-12x^2-5x+15}=\frac{2(16x^4-25)}{(4x^3-12x^2)+(-5x+15)}=\frac{2(4x^2-5)(4x^2+5)}{4x^2(x-3)+-5(x-3)}$

$=\frac{2\cancel{(4x^2-5)}(4x^2+5)}{ \cancel{(4x^2-5)}(x-3)}=\frac{2(4x^2+5)}{x-3}$

 

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ: 

$\mathbf{7}\mathbf{)}\mathbf{ }\frac{3x^{2}y}{14c^{2}d} \times \frac{28cd}{12x^3{y}^2}$

$\frac{3x^{2}y}{14c^{2}d} \times \frac{28cd}{12x^3{y}^2}=\frac{\cancel{3\times }\cancel{x^2}\times \cancel{y}}{\cancel{2}\times \cancel{7}\times \cancel{c}\times c\times \cancel{d} }\times \frac{\cancel{2}\times \cancel{2}\times \cancel{7}\times \cancel{c}\times \cancel{d}}{\cancel{2}\times 2\times \cancel{3}\times \cancel{x^2}\times x\times \cancel{y}\times y }=\frac{1 }{2cxy}$

$\mathbf{8}\mathbf{)}\mathbf{ }\frac{2d+2}{d^2+8d+16} \times \frac{d^2+d-12}{d+1}$

$\frac{2d+2}{d^2+8d+16} \times \frac{d^2+d-12}{d+1}=\frac{2\cancel{(d+1)}}{\cancel{(d+4)}(d+4)}\times \frac{\cancel{(d+4)}(d-3)}{\cancel{d+1}} =\frac{2(d-3)}{d+4}$

---

 

$\mathbf{9}\mathbf{)}\mathbf{ }\frac{x^2-16}{3x^3}\times \frac{x^2}{x^2+x-12}$

$\frac{x^2-16}{3x^3}\times \frac{x^2}{x^2+x-12}=\frac{(x-4)\cancel{(x+4)}}{3\times \cancel{x^2}\times x}\times \frac{\cancel{x^2}}{\cancel{(x+4)}(x-3)}=\frac{x-4}{3x(x-3)}$

 

$\mathbf{10}\mathbf{)} \frac{x^2-3x}{x-2} \times \frac{x^2+x-6}{x}$

$\frac{x^2-3x}{x-2} \times \frac{x^2+x-6}{x}=\frac{\cancel{x}(x-3)}{\cancel{x-2}}\times \frac{(x+3)\cancel{(x-2)}}{\cancel{x}}=(x-3)(x+3) =x^2-9$

 

$\mathbf{11}\mathbf{)}\mathbf{ }\frac{x^2-4x}{x-1} \times \frac{x^2+3x-4}{2x}$

$\frac{x^2-4x}{x-1} \times \frac{x^2+3x-4}{2x}=\frac{\cancel{x}(x-4)}{\cancel{x-1}}\times \frac{\cancel{(x-1)}(x+4)}{2\times \cancel{x}}=\frac{(x-4)(x+4)}{2}$

 

 

$\mathbf{12}\mathbf{)} \frac{b^2+12b+11}{b^2-9}\times \frac{b^3+27}{b^2+20b+99}$

$\frac{b^2+12b+11}{b^2-9}\times \frac{b^3+27}{b^2+20b+99}=\frac{\cancel{(b+11)}(b+1)}{(b-3)\cancel{(b+3)}}\times \frac{\cancel{(b+3)}(b^2-3b+9)}{\cancel{(b+11)}(b+9)}=\frac{(b+1)(b^2-3b+9)}{(b-3)(b+9)}$

 

 

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ: 

$\mathbf{13}\mathbf{)}\mathbf{ }\frac{21x^3 y^2}{12 a{b}^2}÷\frac{3x^2 y^2}{24 a^3}$

$\frac{21x^3 y^2}{12 a{b}^2}÷\frac{3x^2 y^2}{24 a^3}=\frac{21x^3 y^2}{12 a{b}^2}\times \frac{24 a^3}{3x^2 y^2}$

$=\frac{\cancel{3}\times 7\times \cancel{x^2}\times x\times \cancel{y^2}}{\cancel{3}\times \cancel{4}\times \cancel{a}\times b^2}\times \frac{\cancel{4}\times \cancel{3}\times 2\times a^2\times \cancel{a} }{\cancel{3}\times \cancel{x^2}\times \cancel{y^2}}=\frac{14x{a}^2}{b^2}$

---

 

$\mathbf{14}\mathbf{)}\mathbf{ }\frac{x^2+x-2}{x^2+5x+6}÷\frac{x^2+2x-3}{x^2+7x+12}$

$\frac{x^2+x-2}{x^2+5x+6}÷\frac{x^2+2x-3}{x^2+7x+12}=\frac{x^2+x-2}{x^2+5x+6}\times \frac{x^2+7x+12}{x^2+2x-3}$

$=\frac{\cancel{(x+2)}\cancel{(x-1)}}{(x+3)\cancel{(x+2)}}\times \frac{\cancel{(x+3)}(x+4)}{\cancel{(x+3)}\cancel{(x-1)}}=\frac{x+4}{x+3}$

 

$\mathbf{15}\mathbf{)}\mathbf{ }\frac{p}{p-4}÷\frac{{\mathrm{p}}^2}{p^2-5p+4}$

$\frac{p}{p-4}÷\frac{{\mathrm{p}}^2}{p^2-5p+4}=\frac{p}{p-4}\times \frac{p^2-5p+4}{{\mathrm{p}}^2}=\frac{\cancel{p}}{\cancel{p-4}}\times \frac{\cancel{(p-4)}(p-1) }{ \cancel{\mathrm{p}}\times \mathrm{p}}=\frac{p-1}{p}$

 

$\mathbf{16}\mathbf{)} \frac{g^2-4g-21}{4g^2+12g}÷(g-7)$

$\frac{g^2-4g-21}{4g^2+12g}÷(g-7)=\frac{{\mathrm{g}}^2-4\mathrm{g}-21}{4{\mathrm{g}}^2+12\mathrm{g}}\times \frac{1}{g-7}=\frac{\cancel{(g-7)}\cancel{(g+3)}}{4g\cancel{(g+3)}}\times \frac{1}{\cancel{g-7}}=\frac{1}{4g}$

 

$\mathbf{17}\mathbf{)}\mathbf{ }\mathbf{ }\frac{x^2-25}{2x-2}÷\frac{x^2+10x+25}{x^2+4x-5}$

$\frac{x^2-25}{2x-2}÷\frac{x^2+10x+25}{x^2+4x-5}=\frac{x^2-25}{2x-2}\times \frac{x^2+4x-5}{x^2+10x+25}$

$=\frac{(x-5)\cancel{(x+5)}}{2\cancel{(x-1)}}\times \frac{\cancel{(x+5)}(\cancel{x-1)}}{\cancel{(x+5)}\cancel{(x+5)}}=\frac{x-5}{2}$

 

$\mathbf{18}\mathbf{)} \frac{x+2}{3x+12}÷\frac{x+2}{x^2-16}$

$\frac{x+2}{3x+12}÷\frac{x+2}{x^2-16}=\frac{x+2}{3x+12}\times \frac{x^2-16}{x+2}=\frac{\cancel{x+2}}{3\cancel{(x+4)}}\times \frac{(x-4)\cancel{(x+4)}}{\cancel{x+2}}=\frac{x-4}{3}$

 

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ:

$\mathbf{19}\mathbf{)}\mathbf{ }\frac{\frac{x^3 y^3}{c{d}^4 }}{\frac{x^2 y}{c^2 d}}$

$\frac{\frac{x^3{y}^3}{c{d}^4}}{\frac{x^2 y}{c^{2}d}}=\frac{x^3{y}^3}{c{d}^4 }÷\frac{x^{2}y}{c^{2}d}=\frac{x^3{y}^3}{c{d}^4 }\times \frac{c^{2}d}{x^{2}y}=\frac{\cancel{x^2}\times x\times y^2\times {\cancel{y}}^{ }}{\cancel{c}\times d^3\times \cancel{d} }\times \frac{\cancel{c}\times c\times \cancel{d}}{\cancel{x^2} \cancel{y}}=\frac{x{y}^{2}c}{d^3}$

 

$\mathbf{20}\mathbf{)}\mathbf{ }\frac{\frac{4a-8}{a^4-9}}{\frac{a^2-a-2}{a^2+7a+12}}$

$\frac{\frac{4a-8}{a^4-9}}{\frac{a^2-a-2}{a^2+7a+12}}=\frac{4a-8}{a^4-9}÷\frac{a^2-a-2}{a^2+7a+12}=\frac{4a-8}{a^4-9}\times \frac{a^2+7a+12}{a^2-a-2}$

$=\frac{4\cancel{(a-2)}}{(a^2-3)(a^2+3)}\times \frac{(a+4)(a+3)}{\cancel{(a-2)}(a+1)}=\frac{4(a+4)(a+3)}{(a^2-3)(a^2+3)}$

 

$\mathbf{21}\mathbf{)}\mathbf{ }\frac{\frac{8x^2-10x-3}{10x^2+35x-20}}{ \frac{2x^2+x-6}{4x^2+18x+8}}$

$\frac{\frac{8x^2-10x-3}{10x^2+35x-20}}{ \frac{2x^2+x-6}{4x^2+18x+8}}=\frac{8x^2-10x-3}{10x^2+35x-20}÷\frac{2x^2+x-6}{4x^2+18x+8}$

$=\frac{8x^2-10x-3}{10x^2+35x-20}\times \frac{4x^2+18x+8}{2x^2+x-6}$

$=\frac{(4x+1)(2x-3)}{5(2x^2+7x-4)}\times \frac{2(2x^2+9x+4)}{(2x-3)(x+2)}$

$=\frac{(4x+1)\cancel{(2x-3)}}{5(2x-1)\cancel{(x+4)} }\times \frac{2(2x+1)\cancel{(x+4)} }{\cancel{(2x-3)}(x+2)}$

$=\frac{2(4x+1)(2x+1)}{5(2x-1)(x+2)}$

 

 

أجدُ مساحةَ كلٍّ منَ الشكلينِ الآتيينِ بدلالةِ x في أبسطِ صورةٍ:

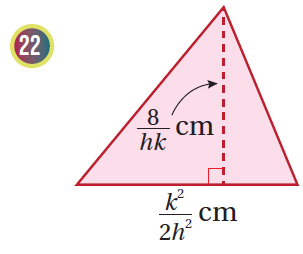
الحل: 

مساحة المثلث= نصف طول القاعدة مضروبًا في الارتفاع                       أفرض مساحة المثلث هو $A$ $A=\frac{1}{2}\times \frac{k^2}{2h^2}\times \frac{8}{hk}=\frac{1}{\cancel{2}}\times \frac{k\times \cancel{k}}{\cancel{2}\times h^2}\times \frac{\cancel{2}\times \cancel{2}\times 2}{h\times \cancel{k}}=\frac{2k}{h^3}c{m}^2$

 

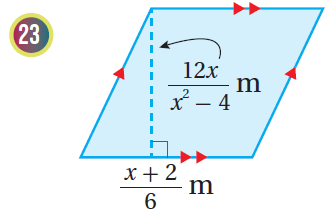
مساحة متوازي الأضلاع = طول القاعدة مضروبًا في الارتفاع  أفرض مساحة متوازي الأضلاع هو $B$ $B=\frac{x+2}{6}\times \frac{12x}{x^2-4}=\frac{\cancel{x+2}}{\cancel{6}}\times \frac{2\times \cancel{6}\times x}{(x-2)\cancel{(x+2)}}=\frac{2x}{x-2}c{m}^2$

 

---

 

24) أكتبُ النسبةَ بينَ محيطِ الشكلِ المُجاوِرِ ومساحتِهِ في صورةِ مقدارٍ  جبريٍّ نسبيٍّ في أبسطِ صورةٍ.

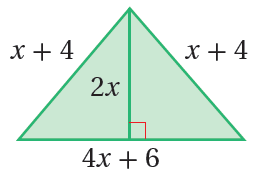
الحل: 

أفرض محيط المثلث هو L

محيط المثلث يساوي مجموع أطوال أضلاعه 

$L=x+4+x+4+4x+6=6x+14$

أفرض مساحة المثلث هو A

مساحة المثلث = نصف طول القاعدة مضروبًا في الارتفاع   

$A=\frac{1}{\cancel{2}}\times (4x+6)\times \cancel{2}x=x(4x+6)$

نسبة محيط المثلث إلى مساحته = $\frac{\mathrm{L}}{\mathrm{A}}$

$\frac{L}{A}=\frac{6x+14}{x(4x+6)}=\frac{\cancel{2}(3x+7)}{\cancel{2}x(2x+3)}=\frac{(3x+7)}{x(2x+3)}$

 

 

25) شموعٌ: في الشكلِ المُجاوِرِ شمعتانِ لهُما الحجمُ نفسُهُ،وإحداهُما أسطوانيةٌ، والأُخرى مخروطيةٌ. أكتبُ مقدارًا نسبيًّا يُمثِّلُ ارتفاعَ الشمعةِ المخروطيةِ بدلالةِ x في أبسطِ صورةٍ.

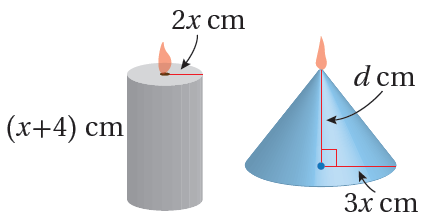
الحل: 

حجم الأسطوانة = مساحة القاعدة$\times$الارتفاع 

حجم المخروط = $\frac{1}{3}$ مساحة القاعدة$\times$الارتفاع 

حجم الأسطوانة = حجم المخروط (مُعطى)	$\mathrm{\pi }{\left(2\mathrm{x}\right)}^2(\mathrm{x}+4)=\frac{1}{3}\times \mathrm{\pi }{\left(3\mathrm{x}\right)}^2\times \mathrm{d}$
بالتبسيط	$\mathrm{\pi }\times 4{\mathrm{x}}^2(\mathrm{x}+4)=\frac{1}{\cancel{3}}\times \mathrm{\pi }\times \cancel{3}\times 3\times {\mathrm{x}}^2\times \mathrm{d}$
بالتبسيط	$\mathrm{\pi }\times 4{\mathrm{x}}^2 (\mathrm{x}+4) = 3{\mathrm{\pi x}}^2\times \mathrm{d}$
بقسمة طرفي المعادلة على $3{\mathrm{\pi x}}^2$	$\frac{\cancel{\mathrm{\pi }}\times 4\cancel{{\mathrm{x}}^2 }(\mathrm{x}+4) }{ 3\cancel{\mathrm{\pi }}\cancel{{\mathrm{x}}^2}}=\mathrm{d}$
ارتفاعَ الشمعةِ المخروطيةِ بدلالةِ x في أبسطِ صورةٍ	$d = \frac{4x+16}{3} cm$

 

---

 

26) أحُلُّ المسألةَ الواردةَ بدايةَ الدرسِ.

مسألةُ اليومِ: يُبيِّنُ الشكلُ المُجاوِرُ شاشةَ حاسوبٍ، طولُها $\frac{x^2}{x^2-2x-15}$ وحدة  وعرضُها $\frac{x-5}{x}$ وحدة. أجدُ مساحةَ الشاشةِ بدلالةِ x في أبسطِ صورةٍ.

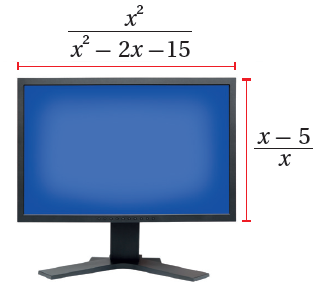الحل : 

مساحة المستطيل = الطول $\times$ العرض 

أفرض مساحة المستطيل هو A

$A=\frac{x^2}{x^2-2x-15}\times \frac{x-5}{x}=\frac{x\times \cancel{x}}{\cancel{(x-5)}(x+3)}\times \frac{\cancel{x-5}}{\cancel{x}}=\frac{x}{x+3} \mathrm{مربعة} \mathrm{وحدة}$

 

مهاراتُ التفكيرِ العليا

27) مسألةٌ مفتوحةٌ: أكتبُ مقدارًا نسبيًّا أبسطُ صورةٍ لهُ هيَ: $\frac{1}{2x+1}$

الحل : 

$\frac{2x-1}{4x^2-1} = \frac{\cancel{2x-1}}{\cancel{(2x-1)}(2x+1)}= \frac{1}{2x+1}$

 

---

 

28) أكتشفُ المختلفَ: أيُّ المقاديرِ النسبيةِ الآتيةِ مختلفٌ، مُبرِّرًا إجابتي؟

الإجابة : 

المقدار النسبي المختلف هو  $\frac{x^2+6x+8}{x^2+4x}$ لأن جميع المقادير النسبية الأخرى كُتبت بأبسط صورة باستثناء هذا المقدار . 

المقدار النسبي بأبسط صورة  :  $\frac{x^2+6x+8}{x^2+4x} =\frac{\cancel{(x+4)}(x+2)}{x\cancel{(x+4)}}=\frac{x+2}{x}$

---

 

29) أكتشفُ الخطأَ: أكتشفُ الخطأَ في الحَلِّ الآتي، ثمَّ أُصحِّحُهُ.

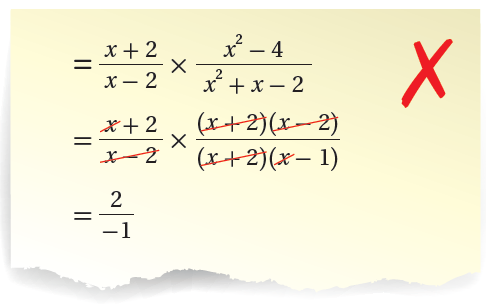
الإجابة : 

الخطأ في عملية اختصار العوامل المشتركة بين البسط والمقام 

الحل الصحيح :

$=\frac{x+2}{x-2}\times \frac{x^2-4}{x^2+x-2}=\frac{x+2}{\cancel{x-2}}\times \frac{\cancel{(x+2)}\cancel{(x-2)}}{\cancel{(x+2)}(x-1)}=\frac{x+2}{x-1}$

---

 

30) تحدٍّ: هلْ يُعَدُّ المقدارُ $x - 2y$ مُكافِئًا للمقدارِ  $\frac{1}{\frac{x^2-4y^2}{x+2y}}$

الحل : 

أكتب المقدار بأبسط صورة :

$\frac{1}{\frac{x^2-4y^2}{x+2y}}=1÷\frac{x^2-4y^2}{x+2y}=1\times \frac{x+2y}{x^2-4y^2}$

$\frac{\cancel{x+2y}}{(x-2y)\cancel{(x+2y)} }=\frac{1}{x-2y}$

إذن: $x-2y$ لا يكافئ المقدار  $\frac{1}{\frac{x^2-4y^2}{x+2y}}$

أسئلة كتاب التمارين

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ :

$1) \frac{3x^2+6x}{12x^2}=\frac{\cancel{3}\cancel{x}(x+2)}{\cancel{3}\times 4\times \cancel{x}\times x}=\frac{x+2}{4x}$

 

$2) \frac{y^2-7y-18}{9-y}=\frac{(y-9)(y+2)}{9-y}=\frac{-\cancel{(9-y)}(y+2)}{\cancel{9-y}}=-(y+2)$

 

$3) \frac{4w^3-36w}{8w^3-48w^2+72w}=\frac{4w(w^2-9)}{8w(w^2-6w+9)}=\frac{\cancel{4}\cancel{w}\cancel{(w-3)}(w+3)}{2\times \cancel{4}\cancel{w}\cancel{(w-3)}(w-3)}=\frac{w+3}{2(w-3)}$

 

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ: 

$4) \frac{5a^3 b^2}{8w{y}^4}\times \frac{12 w^2 y^3}{10a^2 b^3}=\frac{3aw}{4yb}$

     

$5) \frac{6x^4 b^2}{5w{y}^4}÷\frac{4x^2 b^3}{10w^4 y^2}=\frac{6x^4 b^2}{5w{y}^4}\times \frac{10w^4 y^2}{4x^2 b^3}=\frac{3x^2{w}^3}{b{y}^2}$

                                              

$6) \frac{y-z}{6}\times \frac{12}{y^2-z^2}=\frac{2}{y+z}$

   

$7) \frac{n^2}{2n-8}÷\frac{3n}{n^2-16}=\frac{n^2}{2n-8}\times \frac{n^2-16}{3n}$

$\frac{n\times \cancel{n}}{2\cancel{(n-4)}}\times \frac{\cancel{(n-4)}(n+4)}{3\cancel{n}}=\frac{n(n+4)}{6}$

                                                                                                  

$8) \frac{x+3}{8x+4}\times \frac{4x^2-1}{x^2+6x+9}=\frac{\cancel{x+3}}{4\cancel{(2x+1)}}\times \frac{(2x-1)\cancel{(2x+1)}}{\cancel{(x+3)}(x+3)}=\frac{2x-1}{4(x+3)}$

 

$9) \frac{5x-5}{x^2-16}÷\frac{10x^2-10x}{6x-24}=\frac{5x-5}{x^2-16}\times \frac{6x-24}{10x^2-10x}$

$=\frac{ 5(x-1) }{ (x-4)(x+4)}\times \frac{6(x-4)}{10x(x-1) }=\frac{ \cancel{5}(\cancel{x-1)} }{\cancel{ (x-4)}(x+4)}\times \frac{\cancel{2}\times 3\cancel{(x-4)}}{\cancel{2}\times \cancel{5}x\cancel{(x-1) }}=\frac{3}{x(x+4)}$

 

$10) \frac{2a^2-9a-5}{a^2-9a+20}\times \frac{4-a}{2a^2+a}=\frac{(2a+1)(a-5)}{(a-4)(a-5)}\times \frac{4-a}{a(2a+1)}$

$=\frac{\cancel{(2a+1)}\cancel{(a-5)}}{\cancel{(a-4)}\cancel{(a-5)}}\times \frac{-\cancel{(a-4)}}{a\cancel{(2a+1)}}=\frac{-1}{a}$

 

$11) \frac{2a^2- 8a+6}{8a+16}÷\frac{9-a^2}{a^2+5a+6}=\frac{2a^2- 8a+6}{8a+16}\times \frac{a^2+5a+6}{9-a^2}$

$=\frac{2(a-3)(a-1)}{8(a+2)}\times \frac{(a+3)(a+2)}{(3-a)(3+a)}$

$=\frac{ \cancel{2}\times -1\cancel{(3-a)}(a-1)}{\cancel{2}\times 4\cancel{(a+2)}}\times \frac{\cancel{(a+3)}\cancel{(a+2)}}{\cancel{(3-a)}\cancel{(3+a)}}=\frac{-(a-1)}{4}$

 

$12) \frac{\frac{1-2b}{b}}{\frac{b-4}{b}}=\frac{1-2b}{b}÷\frac{b-4}{b}=\frac{1-2b}{\cancel{b}}\times \frac{\cancel{b}}{b-4}=\frac{1-2b}{b-4}$

 

$13) \frac{\frac{x^2-16}{5x^2}}{\frac{4-x}{10x}}=\frac{x^2-16}{5x^2}÷\frac{4-x}{10x}=\frac{x^2-16}{5x^2}\times \frac{10x}{4-x}$

$=\frac{-\cancel{(4-x)}(x+4)}{\cancel{5}\times \cancel{x}\times x}\times \frac{\cancel{5}\times 2\cancel{x}}{\cancel{4-x}}=\frac{-2(x+4)}{x}$

 

$14) \frac{\frac{{(x+1)}^2}{x^2-3x}}{\frac{x^2+2x+1}{x^2-9}}=\frac{{(x+1)}^2}{x^2-3x}÷\frac{x^2+2x+1}{x^2-9}$

$=\frac{{(x+1)}^2}{x^2-3x}\times \frac{x^2-9}{x^2+2x+1}$

$=\frac{\cancel{(x+1)}\cancel{(x+1)}}{x\cancel{(x-3)}}\times \frac{\cancel{(x-3}\left)\right(x+3)}{\cancel{(x+1)}\cancel{(x+1})}=\frac{x+3}{x}$

 

$15) \frac{\frac{4x^2-1}{3x^3-6x^2-24x}}{\frac{12x^2+12x-9}{2x^2-5x-12}}=\frac{4x^2-1}{3x^3-6x^2-24x}÷\frac{12x^2+12x-9}{2x^2-5x-12}$

$=\frac{4x^2-1}{3x^3-6x^2-24x}\times \frac{2x^2-5x-12}{12x^2+12x-9}$

$=\frac{\cancel{(2x-1)}(2x+1)}{3x\cancel{(x-4)}(x+2)}\times \frac{\cancel{(2x+3)}\cancel{(x-4)}}{3\cancel{(2x+3)}\cancel{(2x-1)}}=\frac{2x+1}{9x(x+2)}$ 

---

مُعتمِدًا المعلوماتِ المعطاةَ في الشكلِ المجاورِ، أُجيبُ عنِ السؤالينِ الآتيينِ تباعًا: 

16) أجدُ النسبةَ بينَ طولِ المستطيلِ وعرضِهِ في صورةِ مقدارٍ جبريٍّ نسبيٍّ في أبسطِ صورةٍ. 17) أجدُ مساحةَ المستطيلِ في صورةِ مقدارٍ جبريٍّ نسبيٍّ في أبسطِ صورةٍ.

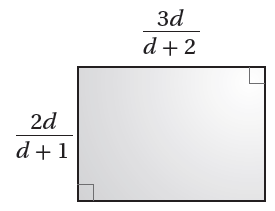الحل : 

16) 

$\frac{\frac{3d}{d+2}}{\frac{2d}{d+1}}=\frac{3d}{d+2}÷\frac{2d}{d+1}=\frac{3\cancel{d}}{d+2}\times \frac{d+1}{2\cancel{d}}=\frac{3(d+1)}{2(d+2)}$

---

17) أفرض مساحة المستطيل = A

$A=\frac{3d}{d+2}\times \frac{2d}{d+1}=\frac{6d^2}{(d+2)(d+1)}$

---

18) أسطوانةٌ مساحةُ قاعدتِها $\left(\frac{x^2+5x-6}{4x}\right) c{m}^2$ ، وارتفاعُها $\left(\frac{x^2-4x}{x^2-5x+4}\right) c{m}^{ }$ أجدُ حجمَ الأسطوانةِ في أبسطِ صورةٍ.

الحل : 

حجم الأسطوانة = مساحة القاعدة $\times$ الارتفاع 

أفرض حجم الأسطوانة $V$

$V=\frac{x^2+5x-6}{4x}\times \frac{x^2-4x}{x^2-5x+4}$

$\frac{(x+6)\cancel{(x-1)}}{4\cancel{x}}\times \frac{\cancel{x}\cancel{(x-4)}}{\cancel{(x-4)}\cancel{(x-1)}}=\frac{x+6}{4} c{m}^3$