رياضيات فصل أول

يوجد في أي مثلث ستة قياسات،هي:ثلاثة أضلاع، وثلاث زوايا.

وإيجاد هذه القياسات يعرف باسم حل المثلث؛إذ تساعد قياسات الزوايا على حل المثلثات في حال كانت بعض قياساتها معروفة،

وذلك باستعمال نسبة الجيب لإيجاد علاقات بين أطوال الأضلاع 

ففي المثلث ABC المرسوم جانبا،يمثل h الارتفاع من النقطة a؛لذا فهو عمودي على القاعدة $\overline{BC}$

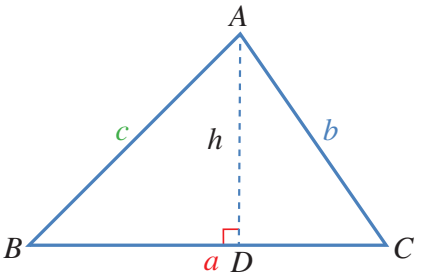
رموز رياضية 

تشير الأحرف الكبيرة A , B , C إلى رؤوس الزوايا ، إنما الأحرف الصغيرة a , b ,c إلى أطوال الأضلاع . 

يمكن الاستفادة من تعريف الجيب في استنتاج بعض العلاقات كما يأتي:

$$\begin{gathered} \sin B=\frac{h}{c} \\ h=c\sin B \\ \sin C=\frac{h}{b} \\ h=b\sin C \\ c\sin B=b\sin \hspace{0.17em}C \\ \frac{c}{\sin C}=\frac{b}{\sin B} \end{gathered}$$

وبالمثل،يمكن استناج العلاقتين الالتيتين عند رسم ارتفاع المثلث من النقطة B بشكل عمودي على AC،أو رسم ارتفاعه من النقطة C عموديا على AB 

$$\begin{gathered} \frac{a}{\sin A}=\frac{c}{\sin \hspace{0.17em}C} \\ \frac{a}{\sin A}=\frac{b}{\sin B} \end{gathered}$$

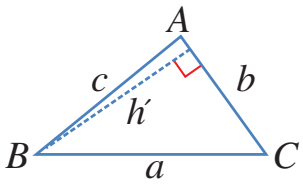
عند دمج هذه العلاقات الثلاث معا،ينتج قانون الجيوب

$\frac{a}{\sin \hspace{0.17em}A}=\frac{b}{\sin \hspace{0.17em}B}=\frac{c}{\sin C}$

يستعمل قانون الجيوب لحل المثلث الذي علمت ثلاثة من قياساته،وذلك في الحالتين الآتيتين:

1) ضلع واحد وزاويتان $\left(SAA \mathrm{او،}ASA\right)$

2) ضلعان وزاوية مقابلة لأحدهما $\left(SSA\right)$

يبين الشكل الآتي هاتين الحالتين:

---

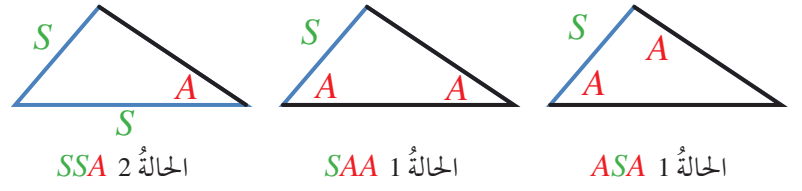
مثال 

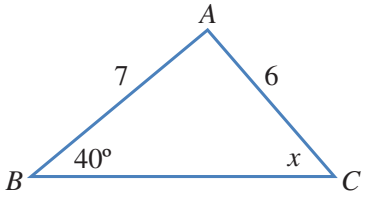
أجد قيمة x في المثلث ABC

$$\begin{gathered} \frac{x}{\sin 84°}=\frac{25}{\sin 47°} \\ x=\frac{25 \sin 84°}{\sin 47°} \\ \approx 34cm \end{gathered}$$

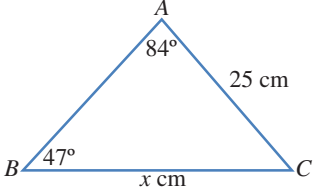
يمكن أيضا استعمال قانون الجيوب لإيجاد قياس زاوية مجهولة فيي المثلث

مثال 

أجد قيمة x في المثلث ABC

$$\begin{gathered} \frac{\sin x}{7}=\frac{\sin 40°}{6} \\ \sin x=\frac{7\sin 40°}{6} \\ \approx 0.7499 \\ x={\sin }^{-1}\left(0.7499\right) \\ \approx 48.6° \end{gathered}$$

---

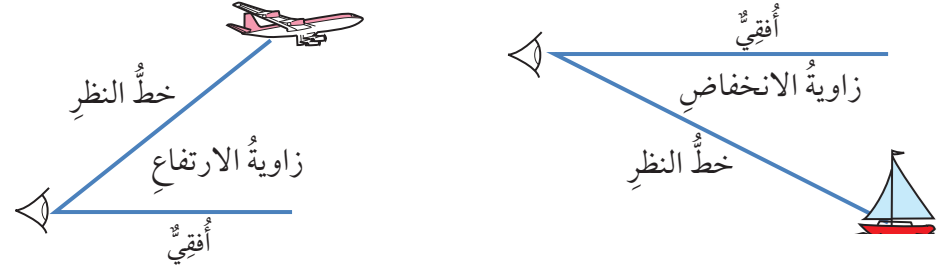
• عندما أنظر إلى طائرة في السماء،فإن الزاوية المحصورة بين الخط الواصل بين عيني والطائرة وخط نظري أفقيا تسمى زاوية الارتفاع.
• وإذا وفقت على تلة ساحلية،ثم نظرت إلى قارب أسفل مني،فإن الزاوية المحصورة بين الخط الواصل بين عيني والقارب وخط نظرة أفقيا تسمى زاوية الانخفاض.ولهاتين الزاويتين أهمية كبيرة عند حل المسائل الحياتية باستعمال النسب المثلثية 

---

مثال:من الحياة

يقع برج ارتفاعه h متر على تلة، وقد رصدت قمة البرج A من النقطة B التي تبعد عن قاعدة البرج $25m$ فكان قياس زاوية ارتفاعها $50°$، ثم رصدت قمة التلة من النقطة B نفسها فكان قياس زاوية ارتفاعها $20°$.ما ارتفاع البرج h؟

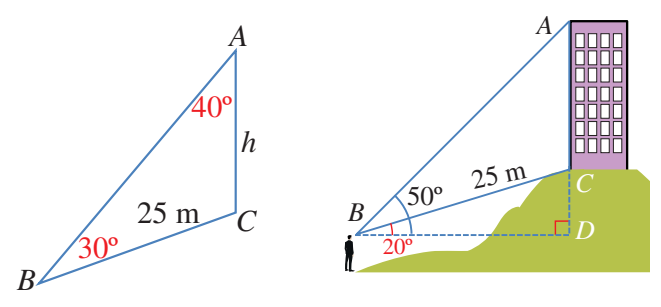
أجد أولا قياس الزاوية ABC:

$m\angle ABC=50°-20°=30°$

ثم أجد قياس الزاوية BAD:

$m\angle BCD=180°-90°-50°=40°$

ارتفاع البرج هو طول الضلع AC في المثلث BAC.استعمل قانون الجيوب لحل هذا المثلث

بعد ذلك استعمل قانون الجيوب في المثلث BAC لإيجاد ارتفاع البرج:

$$\begin{gathered} \frac{h}{\sin 30°}=\frac{25}{\sin 40°} \\ h=\frac{25 \sin 30°}{\sin 40°} \\ h\approx 19.45m \end{gathered}$$

إذا،ارتفاع البرج هو:$19.45m$

---

مثال:من الحياة 

التقطت محطتا خفر السواحل A وB نداء استغاثة من سفينة عند النقطة C في البحر،وقد حددت المحطة A اتجاه السفينة عند $040°$،وحددت المحطة B اتجاه السفينة عند $330°$.إذا كانت B شرقي A وكانت المسافة بين المحطتين $120km$،فكم تبعد السفينة عن المحطة A؟

يجب أولا إيجاد قياس الزاوية C:

قياس الزاوية BAC هو $50°$(لأنها متممة للزاوية التي قياسها $40°$)

وقياس الزاوية ABC هو $\left(330°-270°=60° \mathrm{لان}\right)60°$.إذن:

$m\angle ACB=180°-60°-50°=70°$

ثم استعمال قانون الجيوب:

$$\begin{gathered} \frac{b}{\sin B}=\frac{c}{\sin C} \\ \frac{b}{\sin 60°}=\frac{120}{\sin 70°} \\ b=\frac{120\times \sin 60°}{\sin 70°} \\ \approx 110.59km \end{gathered}$$

---

---