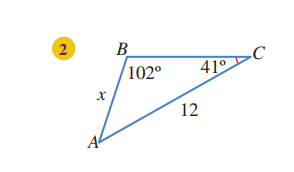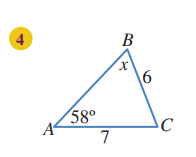رياضيات فصل أول

العاشر

الشرح الملخص أوراق العمل حل اسئلة الدرس النتاجات

أتحقق من فهمي صفحة 119

أجد قيمة x في المثلث RST المبين جانبا

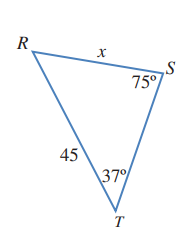
الحل:

$\frac{x}{s i n 37} = \frac{45}{s i n 75}$

$x s i n 75 = 45 s i n 37$

$x = \frac{45 s i n 37}{s i n 75}$

$x = \frac{45 \times 0.602}{0.966}$

$x = 28.043$

أتحقق من فهمي صفحة 120

أجد قيمة x في المثلث RST

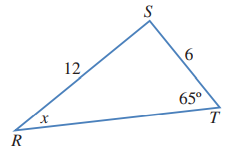
الحل:

$\frac{6}{s i n x} = \frac{12}{s i n 65}$

$12 s i n x = 6 s i n 65$

$s i n x = \frac{6 \times s i n 65}{12}$

$s i n x = 0.453$

$x = s i n^{- 1} (0.453)$

$x = 26.9$

أتحقق من فهمي صفحة 121

رصد ليث زاوية قمة بناية من النقطة A،فكانت $37 °$ ،ثم سار مسافة $20 m$ باتجاه البناية حتى النقطة C،ثم رصد زاوية قمة البناية،فكانت $67 °$ .أجد ارتفاع البناية

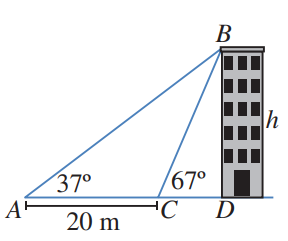
الحل:

$90 - 37 = 53 يساوي A B D الزاوية قياس$

$90 - 67 = 23 يساوي C B D الزاوية قياس$

$53 - 23 = 30 يساوي A B C الزاوية قياس بالتالي$

$\frac{C B}{s i n 37} = \frac{20}{s i n 30}$

$C B s i n 30 = 20 s i n 37$

$C B = \frac{20 \times s i n 37}{s i n 30}$

$C B = 24.07$

$\frac{h}{s i n 67} = \frac{24.07}{s i n 90}$

$h s i n 90 = 24.07 \times s i n 67$

$h = 24.07 \times 0.921$

$h = 22.16$

أتحقق من فهمي صفحة 122

أجد بعد السفينة عن المحطة B في المثال السابق

الحل:

$50 يساوي C A B الزاوية قياس$

$70 يساوي A C B الزاوية قياس$

$\frac{C B}{\sin 50} = \frac{120}{\sin 70}$

$C B \sin 70 = 120 \sin 50$

$C B = \frac{120 \sin 50}{\sin 70}$

$x = \frac{120 \times 0.766}{0.94}$

$x = 97.79$

أتدرب وأحل المسائل صفحة 122

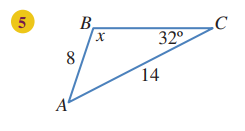
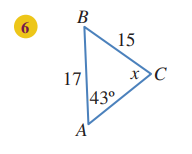
أجد قيمة x في كل من المثلثات الآتية:

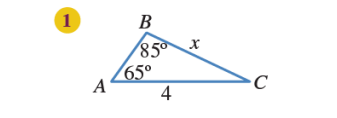
الحل:

$\frac{x}{s i n 65} = \frac{4}{s i n 85}$

$x s i n 85 = 4 s i n 65$

$x = \frac{4 s i n 65}{s i n 85}$

$x = \frac{4 \times 0.906}{0.996}$

$x = 3.639$

$\frac{x}{s i n 41} = \frac{12}{s i n 102}$

$x s i n 102 = 12 s i n 41$

$x = \frac{12 \sin 41}{\sin 102} = \frac{12 \times 0.656}{0.978} = 8.049$

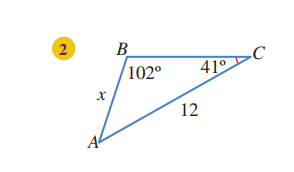
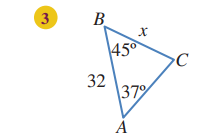
قياس الزاوية C تساوي:

$180 - (45 + 37) = 180 - 82 = 98 °$

$\frac{x}{\sin 37} = \frac{32}{\sin 98}$

$x s i n 98 = 32 s i n 37$

$x = \frac{32 \sin 37}{\sin 98} = \frac{32 \times 0.602}{0.99} = 19 . 459$

$\frac{7}{s i nx} = \frac{6}{s i n 58} 6 s i n x = 7 s i n 58 s i n x = \frac{7 s i n 58}{6} = 0.989 x = s i n^{- 1} (0.989) = 81.6$

$\frac{14}{s i nx} = \frac{8}{s i n 32}$

$8 s i n x = 14 s i n 32$

$s i n x = \frac{14 \sin 32}{8} = 0.927$

$x = s i n^{- 1} (0.927) = 68.02$

$\frac{17}{s i n x} = \frac{15}{s i n 43}$

$15 s i n x = 17 s i n 43$

$s i n x = \frac{17 \sin 43}{15}$

$s i n x = 0.773$

$x = s i n^{- 1} (0.773) = 50.62 °$

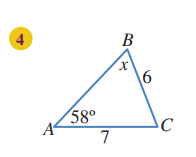
7) أجد قياس الزاوية المنفرجة CBA في الشكل المجاور

$\frac{10}{s i nB} = \frac{7}{s i n 30}$

$7 s i n B = 10 s i n 30$

$s i n B = \frac{10 \sin 30}{7} = 0.714$

$B = s i n^{- 1} (0.714)$

$B = 45.58 °$

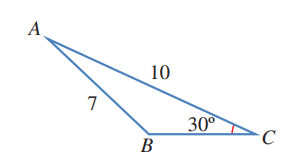
الزاوية B المنفرجة في الربع الثاني وتساوي

$180 - 45.58 = 134.42$

8) خرائط:أحل المسألة الواردة في بداية الدرس

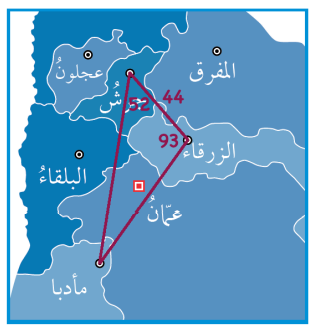
إذا كانت جرش والزرقاء ومأدبا تشكل رؤوس مثلث على الخريطة، والمسافة بين مدينتي الزرقاء وجرش $44 k m$ ،وقياس الزاوية التي تقع عند رأسها مدينة جرش $52 °$ ، وقياس الزاوية التي تقع عند رأسها مدينة الزرقاء $93 °$ ، فهل يمكن بهذه المعلومات حساب المسافة بين مدينتي جرش ومادبا؟

الحل :

المسافة بين جرش و مأدبا تساوي x الزاوية التي يقع رأسها عند مأدبا تساوي 35 .

$\frac{x}{s i n 93} = \frac{44}{s i n 35}$

$x s i n 35 = 44 s i n 93$

$x = \frac{44 \sin 93}{\sin 35} = \frac{44 \times 0.998}{0.574} = 76.5$

9) بحار : ترصد سفينتان في البحر قمة جبل كما في الشكل المجاور . إذا كانت المسافة بين السفينتين 1473m ، فما ارتفاع الجبل عن مستوى سطح البحر ؟

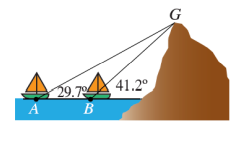
الحل :

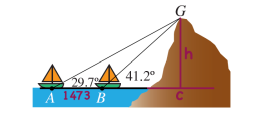
قياس الزاوية AGC يساوي 60.3 = 29.7 - 90

قياس الزاوية BGC يساوي 48.8 = 41.2 - 90

قياس الزاوية AGB يساوي 11.5= 48.8 - 60.3

نجد طول BG

$\frac{BG}{\sin 29.7} = \frac{1473}{\sin 11.5}$

$B G s i n 11.5 = 1473 s i n 29.7$

$B G = \frac{1473 \times \sin 29.7}{\sin 11.5} = 3660.62$

$\frac{h}{\sin 41.2} = \frac{3660.62}{\sin 90}$

$h s i n 90 = 3660.62 \times s i n 41.2$

$h = 3660.62 \times 0.659$

$h = 2411.21$

10) علم الفلك : رصد عامر وهشام من منزليهما نجمًا في السماء في اللحظة نفسها . إذا كانت زاوية رصد هشام للنجم $49.8974 °$ ، وزاوية رصد عامر له $49.9312 °$ والمسافة بينهما 300km ، فأقدر بعد النجم عن الأرض .

الحل :

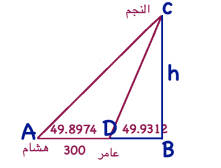
قياس الزاوية ACB يساوي 40.1026 = 49.8974 - 90

قياس الزاوية DCB يساوي 40.0688 = 49.9312 - 90

قياس الزاوية ACD يساوي 0.0338 = 40.0688 - 40.1026

نجد طول DC

$\frac{D C}{s i n 49.8974} = \frac{300}{s i n 0.0338}$

$D C s i n 0.0338 = 300 s i n 49.8974$

$D C = \frac{300 \sin 49.8974}{\sin 0.0338} = 388980.14$

$\frac{h}{\sin 49.9312} = \frac{388980.14}{\sin 90}$

$h = 388980.14 \times s i n 49.9312$

$h = 388980.14 \times 0.765 = 297675.6254$

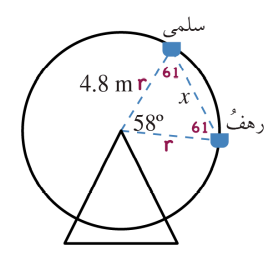
11) مدينة الألعاب: في مدينة الألعاب، جلست سلمى ورهف على مقعدين منفصلين في لعبة الدولاب الدوار كما في الشكل المجاور.أجد المسافة x بينهما

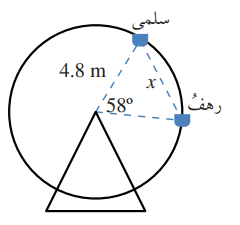
الحل :

$\frac{x}{s i n 58} = \frac{4.8}{s i n 61}$

$x s i n 61 = 4.8 s i n 58$

$x = \frac{4.8 \sin 58}{\sin 61} = \frac{4.8 \times 0.848}{0.875} = 4.65$

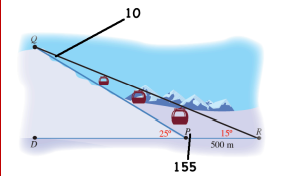
12) رياضة التزلج: يتكون مسار تزلج من جزء مائل،وآخر مستقيم. إذا تزلج محمود من النقطة Q إلى النقطة P، ثم وصل خط النهاية عند النقطة R، وكانت زاوية ارتفاع مسار التزلج عن الأرض $25 °$ ، والمسافة بين النقطتين P وR هي $500 m$ ،وزاية رصد الحكم من نقطة النهاية للمتزلج الذي يقف عند نقطة البداية $15 °$ ،فما طول QP؟

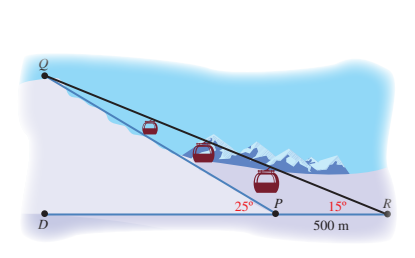
الحل :

$\frac{Q P}{s i n 15} = \frac{500}{s i n 10}$

$Q P s i n 10 = 500 s i n 15$

$Q P = \frac{500 \sin 15}{\sin 10}$

$Q P = \frac{500 \times 0.259}{0.174} = 744.252$

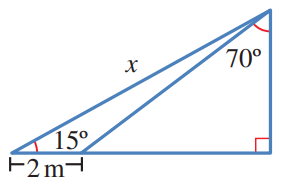
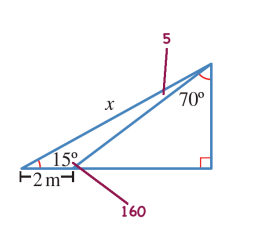
13) أجد قيمة x في الشكل المجاور،مقربا إجابتي إلى أقرب جزء من عشرة

الحل :

$\frac{x}{s i n 160} = \frac{2}{s i n 5}$

$x s i n 5 = 2 s i n 160$

$x = \frac{2 \sin 160}{\sin 5} = \frac{2 \times 0.342}{0.087} = 7.862$

مهارات التفكر العليا

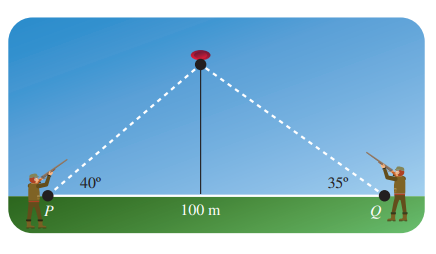
14) تبرير: أطلق قناصان النار على هدف متحرك في المساء في لحظة ما.إذا كانت زاوية إطلاق الأول $40 °$ ،وزاوية إطلاق الثاني $35 °$ ،والمسافة بينهما $100 m$ ،فأيهما سيصيب الهدف أولا؟أبرر إجابتي

الحل :

$\frac{A P}{s i n 35} = \frac{100}{s i n 105}$

$A P s i n 105 = 100 s i n 35$

$A P = \frac{100 \sin 35}{\sin 105} = \frac{100 \times 0.574}{0.966} = 59.42$

$\frac{AQ}{\sin 40} = \frac{100}{\sin 105}$

$A Q s i n 105 = 100 s i n 40$

$A Q = \frac{100 \sin 40}{\sin 105} = \frac{100 \times 0.643}{0.966} = 66.563$

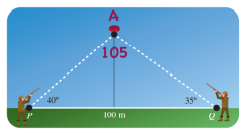
المسافة بين القناص الأول و الهدف هي 59.42 والمسافة بين القناص الثاني والهدف هي 66.563

إذا القناص الأول يصيب الهدف أولًا ؛ لأن المسافة بينه و بين الهدف أقل .

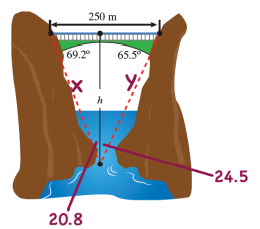
15) تحد: مر قارب أسفل جسر طوله $250$ مترا. وقد رصد الشخص الذي في القارب الزاويتين اللتين عند طرفي الجسر، فكانتا $65.5 ° و ، 69.2 °$ ، أجد ارتفاع الجسر عن القارب

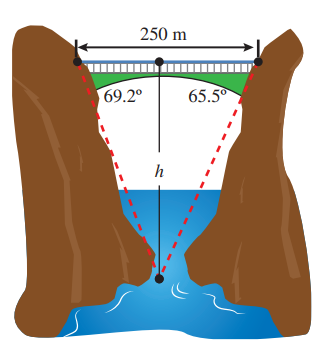
الحل :

$\frac{x}{\sin 65.5} = \frac{250}{\sin 45.3}$

$x \sin 45.3 = 250 \sin 65.5$

$x = \frac{250 \sin 65.5}{\sin 45.3} = \frac{250 \times 0.909}{0.711} = 319.62$

$\frac{h}{\sin 69.2} = \frac{319.62}{\sin 90}$

$h \sin 90 = 319.62 \sin 69.2$

$h = 319.62 \sin 69.2 = 298.789$

16) تبرير: توجهت طائرة من المدينة P إلى المدينة Q، وبعد أن قطعت مسافة $50 k m$ أدرك الطيار وجود خطأ في زاوية الانطلاق مقداره $10 °$ ، فاستدار في الحال، وقطعت الطائرة مسافة $70 k m$ حتى وصلت المدينة Q. إذا كانت سرعة الطائرة ثابتة وتساوي $250 k m / h$ ،فما الوقت الإضافي الذي استغرقه الطيار بسبب خطئه في زاوية الانطلاق؟

$\frac{50}{s i nQ} = \frac{70}{s i n 10}$

$70 \sin Q = 50 \sin 10$

$\sin Q = \frac{50 \sin 10}{70} = 0.124$

$Q = \sin^{- 1} (0.124) = 7 °$

$\frac{PQ}{\sin 163} = \frac{70}{\sin 10}$

$P Q \sin 10 = 70 \sin 163$

$P Q = \frac{70 \sin 163}{\sin 10} = \frac{70 \times 0.292}{0.174} = 118.28$

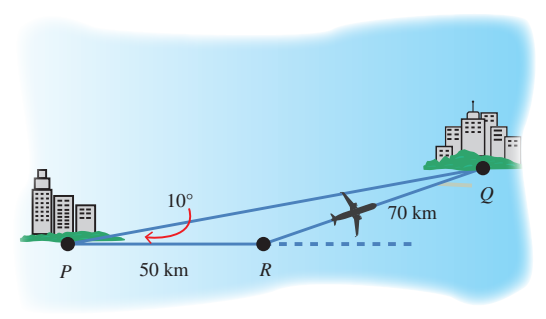
الزاوية R تساوي

$180 - (10 + 7.12) = 180 - 17.12 = 162.88$

$\frac{المسافة}{الزمن} = السرعة$

$\frac{1}{5} \times 60 = 12 m i n يساوي P R وقت بالتالي \frac{50}{250} = \frac{1}{5} هو P R وقت$

$\frac{7}{25} \times 60 = 16.8 m i n يساوي R Q وقت بالتالي \frac{70}{250} = \frac{7}{25} هو R Q وقت$

$\frac{59.14}{125} \times 60 = 28.39 m i n يساوي P Q وقت بالتالي \frac{118.28}{250} = \frac{59.14}{125} هو P Q وقت$

كتاب التمارين

أجد القياس المجهول في كل من المثلثات الآتية:

$C + 15 ° + 35 ° = 180 \Rightarrow C = 130 °$

$\frac{a}{\sin 35} = \frac{5}{\sin 130} \Rightarrow a = \frac{5 \sin 35}{\sin 130} \Rightarrow a = 3.7$

$\frac{b}{\sin 15} = \frac{5}{\sin 130} \Rightarrow b = \frac{5 \sin 15}{\sin 130} \Rightarrow b = 1.7$

$C + 45 ° + 90 ° = 180 \Rightarrow C = 85 °$

$\frac{a}{\sin 40} = \frac{7}{\sin 45} \Rightarrow a = \frac{7 \sin 40}{\sin 45} \Rightarrow a = 6.4$

$\frac{c}{\sin 85} = \frac{7}{\sin 45} \Rightarrow c = \frac{7 \sin 85}{\sin 45} \Rightarrow b = 9.9$

$A + 125 ° + 30 ° = 180 \Rightarrow C = 25 °$

$\frac{a}{\sin 25} = \frac{10}{\sin 30} \Rightarrow a = \frac{10 \sin 25}{\sin 30} \Rightarrow a = 8.5$

$\frac{c}{\sin 125} = \frac{10}{\sin 30} \Rightarrow c = \frac{10 \sin 125}{\sin 30} \Rightarrow c = 16.4$

$C + 30 ° + 100 ° = 180 \Rightarrow C = 50 °$

$\frac{a}{\sin 100} = \frac{6}{\sin 30} \Rightarrow a = \frac{6 \sin 100}{\sin 30} \Rightarrow a = 11.8$

$\frac{c}{\sin 50} = \frac{6}{\sin 30} \Rightarrow c = \frac{6 \sin 50}{\sin 30} \Rightarrow c = 9.2$

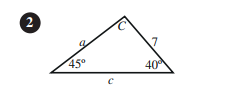
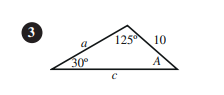
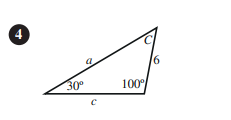
أجد القياس المجهول في المثلث ABC في كل من الحالات الآتية :

$5 . a = 3, b = 2, A = 50 °$

$\frac{3}{\sin 50} = \frac{2}{\sin B} \Rightarrow \sin B = \frac{2 \sin 50}{3} = 0.5$

$B = \sin^{- 1} (0.5) \Rightarrow B = 30 °$

$C + 30 ° + 50 ° = 180 \Rightarrow C = 100 °$

$\frac{c}{\sin 100} = \frac{3}{\sin 50} \Rightarrow c = \frac{3 \sin 100}{\sin 50} \Rightarrow c = 3.9$

$6 . A = 40 °, B = 20 °, a = 2$

$C + 40 ° + 20 ° = 180 \Rightarrow C = 120 °$

$\frac{c}{\sin 120} = \frac{2}{\sin 40} \Rightarrow c = \frac{2 \sin 120}{\sin 40} \Rightarrow c = 2.7$

$\frac{b}{\sin 20} = \frac{5}{\sin 40} \Rightarrow b = \frac{5 \sin 20}{\sin 40} \Rightarrow b = 1.06$

$7 . a = 2, c = 1, A = 120 °$

$\frac{1}{sinC} = \frac{2}{\sin 120} \Rightarrow \sin C = \frac{\sin 120}{2} = 0.43$

$C = \sin^{- 1} (0.43) \Rightarrow C = 25.5 °$

$B + 25.5 ° + 120 ° = 180 \Rightarrow B = 34.5 °$

$\frac{b}{\sin 34.5} = \frac{2}{\sin 120} \Rightarrow b = \frac{2 \sin 34.5}{\sin 120} \Rightarrow b = 1.3$

$8 . A = 40 °, B = 20 °, a = 2$

$C + 70 ° + 60 ° = 180 \Rightarrow C = 50 °$

$\frac{b}{\sin 60} = \frac{4}{\sin 50} \Rightarrow b = \frac{4 \sin 60}{\sin 50} \Rightarrow c = 4.5$

$\frac{a}{\sin 70} = \frac{4}{\sin 50} \Rightarrow a = \frac{4 \sin 70}{\sin 50} \Rightarrow a = 4.9$

$9 . b = 4, c = 6, B = 20 °$

$\frac{6}{sinC} = \frac{4}{\sin 20} \Rightarrow \sin C = \frac{6 \sin 20}{4}$

$\sin C = 0.5 \Rightarrow C = 30 °$

$A + 30 ° + 20 ° = 180 \Rightarrow A = 130 °$

$\frac{a}{\sin 130} = \frac{4}{\sin 20} \Rightarrow a = \frac{4 \sin 130}{\sin 20} \Rightarrow a = 8.9$

$10 . A = 40 °, B = 40 °, c = 2$

$C + 40 ° + 40 ° = 180 \Rightarrow C = 100 °$

$\frac{a}{\sin 40} = \frac{2}{\sin 100} \Rightarrow c = \frac{2 \sin 40}{\sin 100} \Rightarrow a = 1.3$

$\frac{b}{\sin 40} = \frac{2}{\sin 100} \Rightarrow b = \frac{2 \sin 40}{\sin 100} \Rightarrow b = 1.3$

11. طائرات :رصدت كل من زينة وهناء طائرة ورقية عند مرورها فوق الخط الواصل بينهما ، فكانت زاوية ارتفاعها من موقع زينة $35 °$ ، ومن موقع هناء $40 °$ . إذا كانت المسافة بين زينة وهناء 900m ، فما ارتفاع الطائرة ؟

الحل :

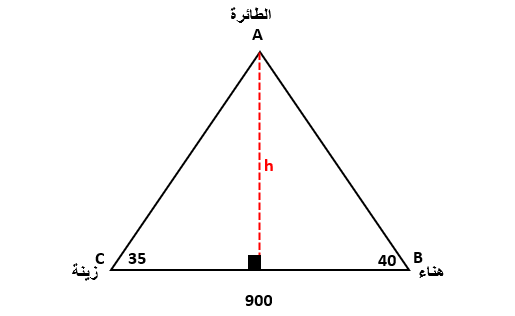
h هو ارتفاع الطائرة

$m < C A B = 180 - 40 - 35 = 105 °$

$\frac{900}{\sin 105} = \frac{CA}{\sin 40}$

$C A = \frac{900 \sin 40}{\sin 105} = 598.9$

$\frac{h}{\sin 35} = \frac{598.9}{\sin 90} \Rightarrow h = s i n 35 \times 598.9 \Rightarrow h = 343.5 m$

12. قوارب :رصد طيار القاربين A و B في البحر عندما مرت طائرته فوق الخط الواصل بينهما ، فكانت زاوية انخفاض القارب الأول $44 °$ و زاوية انخفاض القارب الثاني $37 °$ . إذا كانت المسافة بين القاربين 7km ، فما ارتفاع الطائرة عن سطح البحر ؟

الحل :

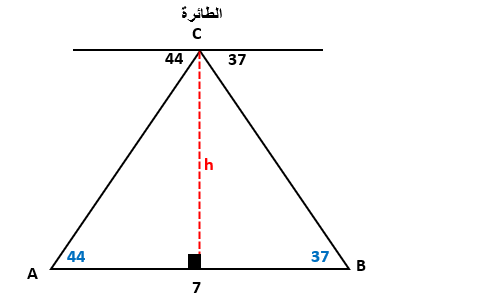
بالتبادل نجد أن

قياس الزاوية A يساوي 44

وقياس الزاوية B يساوي 37

إذ أن h هو ارتفاع الطائرة

$m < A C B = 180 - 37 - 44$

$m < A C B = 99 °$

$\frac{7}{\sin 99} = \frac{CA}{\sin 37} \Rightarrow C A = \frac{7 \sin 37}{\sin 99} = 9.3$

$\frac{h}{\sin 44} = \frac{4.3}{\sin 90} \Rightarrow h = \frac{4.3 \sin 44}{\sin 90} \Rightarrow h = 2.98 k m$

رياضيات فصل أول

العاشر

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS