متوازي الأضلاع
تعريف متوازي الأضلاع :
هو شكل رباعي فيه كل ضلعين متقابلين متوازيان، ويرمز اليه بالرمز
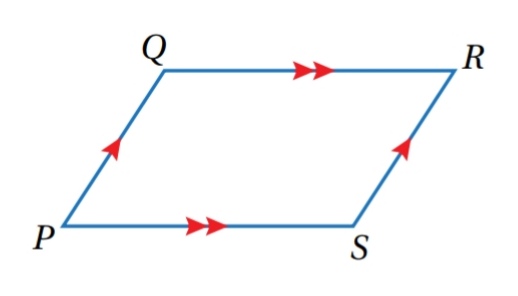
ففي QRSP المبين جانباً و بحسب التعريف
....................................................................................................................................................................................................................................
خصائص متوازي الأضلاع :
- نظرية الأضلاع المتقابلة في متوازي الأضلاع :
إذا كان الشكل الرباعي متوازي أضلاع ، فإن الأضلاع المتقابلة متطابقة
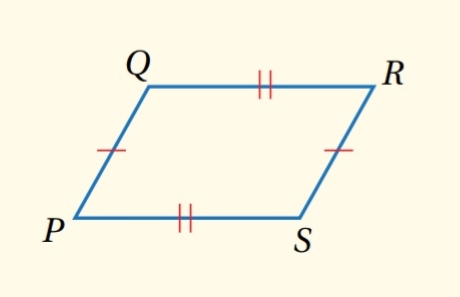
مثال : إذا كان PQRS متوازي أضلاع ، فإن
....................................................................................................................................................................................................................................
- نظرية الزوايا المتقابلة في متوازي الاضلاع :
إذا كان الشكل الرباعي متوازي أضلاع ، فإن الزوايا المتقابلة متطابقة .
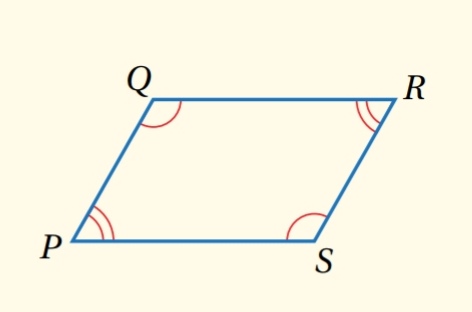
مثال : إذا كان PQRS متوازي أضلاع ، فإن
....................................................................................................................................................................................................................................
مثال ( 1 ) :
أجد قيمة كل من x و y في الشكل المجاور:
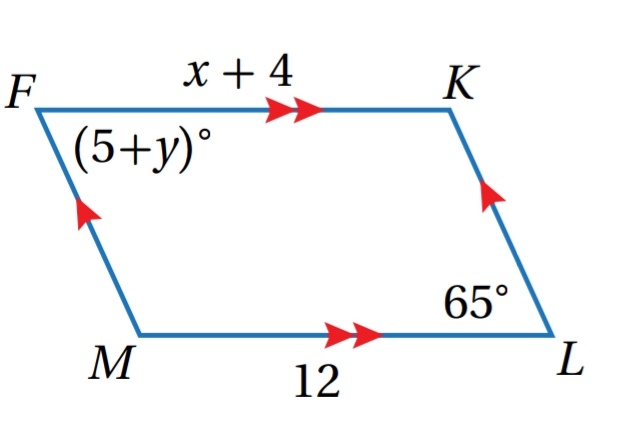
الحل :
بما أن كل ضلعين متقابلين متوازيان في الشكل الرباعي FKLM فإنه متوازي أضلاع ،
ومنه فإنه يمكنني استعمال نظرية الاضلاع المتقابلة في متوازي الاضلاع لإيجاد قيمة x
إذن قيمة x تساوي 8
ويمكنني إيجاد قيمة y باستعمال نظرية الزوايا المتقابلة في متوازي الاضلاع
الزوايا المتقابلة في متوازي الأضلاع متطابقة
تعريف تطابق الزوايا
اكتب المعادلو من دون رمز الزاوية
أطرح 5 من طرفي المعادلة
إذن قيمة y تساوي 60
....................................................................................................................................................................................................................................
الزوايا المتحالفة : هي زوايا مضلع تشترك في الضلع نفسه
مثال : في الشكل المجاور زاويتان متحالفتان، لأنهما تشتركان في الضلع MN. 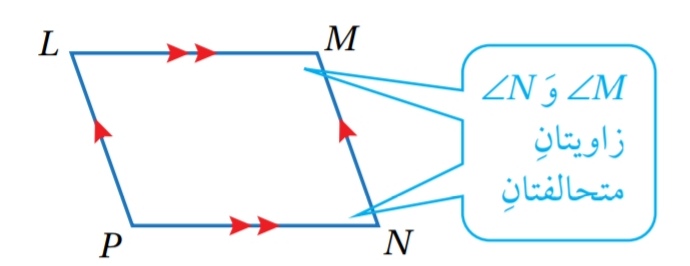
....................................................................................................................................................................................................................................
خصائص متوازي الأضلاع :
- نظرية الزوايا المتحالفة في متوازي الأضلاع :
إذا كان الشكل الرباعي متوازي أضلاع ، فإن كل زاويتين متحالفتين متكاملتان.
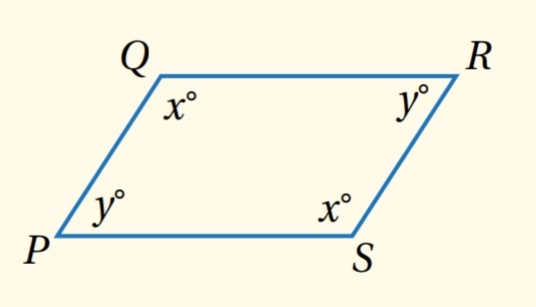
مثال : إذا كان PQRS متوازي أضلاع ، فإن
....................................................................................................................................................................................................................................
- نظرية الزوايا القائمة في متوازي الأضلاع :
إذا كانت إحدى زوايا متوازي الأضلاع قائمة ، فإن زواياه الأربع قوائم
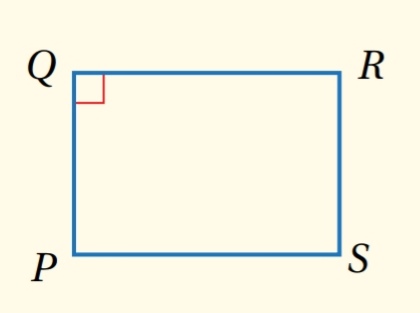
مثال : في إذا كانت قائمة فإن :
قوائم أيضاً .
....................................................................................................................................................................................................................................
مثال ( 2 ) :
في الشكل المجاور ، إذا كان LMNP متوازي أضلاع ، فأجد و
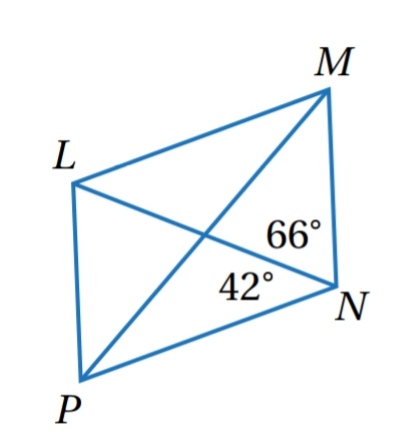
الحل :
أجد
إذن ، تساوي 108
أجد
إذن تساوي 72
....................................................................................................................................................................................................................................
مثال ( 3 ) : مسألة حياتية :
يبين الشكل المجاور جزءاً من مصباح مكتب على شكل متوازي أضلاع ، وتتغير زواياه عند رفعه وخفضه ،
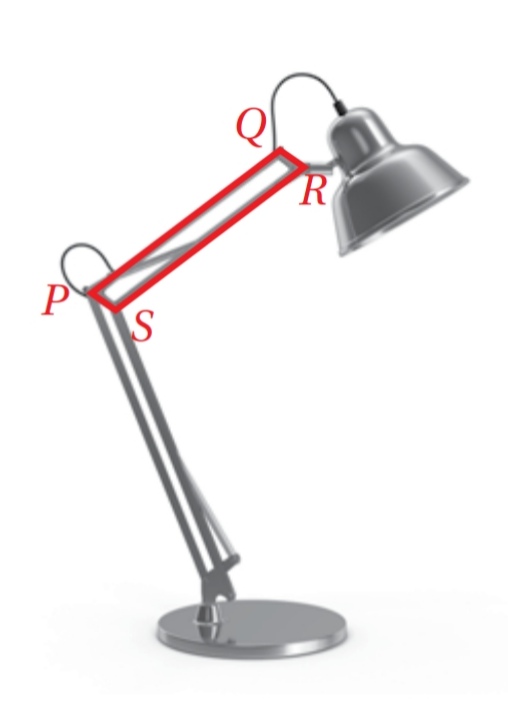
أجد إذا علمت ان
الحل :
المعطيات: - مصباح مكتب على شكل متوازي أضلاع
-
المطلوب : أوجد
لإيجاد قياس الزاوية :
....................................................................................................................................................................................................................................
قطرا متوازي الأضلاع :
- نظرية قطري متوازي الأضلاع :
إذا كان الشكل الرباعي متوازي أضلاع ، فإن قطريه ينصف كل منهما الآخر.
مثال : إذا كان PQRS متوازي أضلاع ، فإن 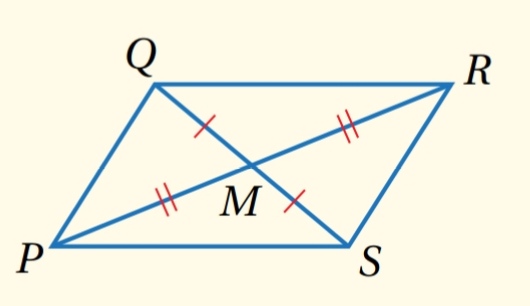
....................................................................................................................................................................................................................................
- نظرية قطر متوازي الأضلاع :
إذا كان الشكل الرباعي متوازي أضلاع ، فإن كل قطر يقسمه الى مثلثين متطابقين
مثال : إذا كان PQRS متوازي أضلاع ، فإن 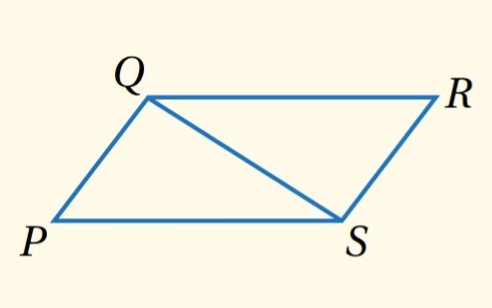
....................................................................................................................................................................................................................................
مثال ( 4 ):
إذا كان ABCD متوازي اضلاع ، فأجد قيمة كل من x و y
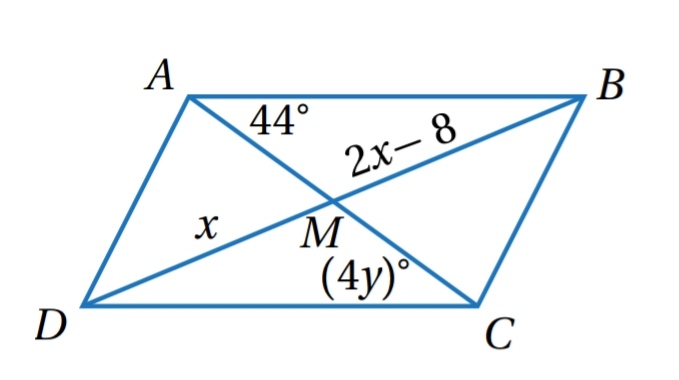
الحل :
أجد قيمة x
أجد قيمة y
....................................................................................................................................................................................................................................
مثال ( 5 ) :
في الشكل المجاور ، إذا كان ABCD و AEFG متوازيي أضلاع ، فأثبت أن باستعمال البرهان ذي العمودين .
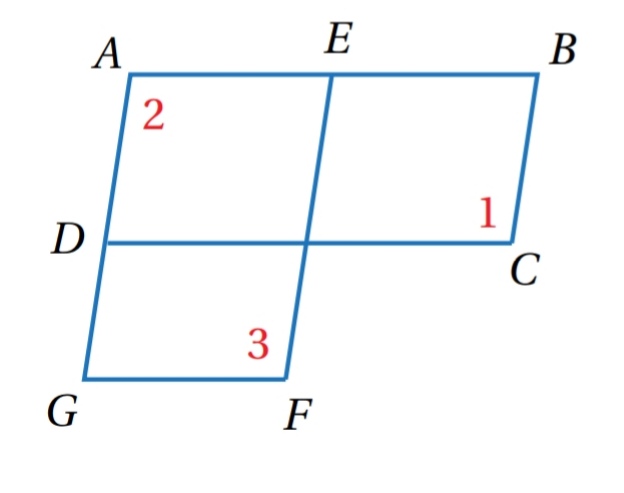
| المبررات | العبارات |
| 1- معطى | 1- ABCD و AEFG متوازيا أضلاع |
| 2- الزوايا المتقابلة في متوازي الاضلاع متطابقة | 2- |
| 3- الزوايا المتقابلة في متوازي الاضلاع متطابقة | 3- |
| 4- بما أن | 4- |
....................................................................................................................................................................................................................................