متوازي الأضلاع :
حل أسئلة أتحقق من فهمي :
اتحقق من فهمي :
أجد قيمة كل من h و g في الشكل المجاور :
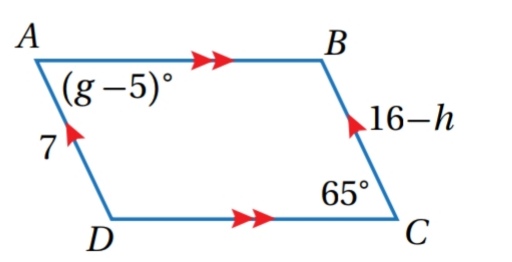
الحل :
باستعمال نظرية الزوايا المتقابلة في متوازي الأضلاع
باستعمال نظرية الاضلاع المتقابة في متوازي الاضلاع :
..............................................................................................................................................................................................................
أتحقق من فهمي:
في الشكل المجاور، إذا كان JKLM متوازي أضلاع، فأجد و
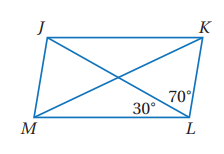
أتحقق من فهمي :
أفترض أن مصباح المكتب عدل لتصبح ، أجد
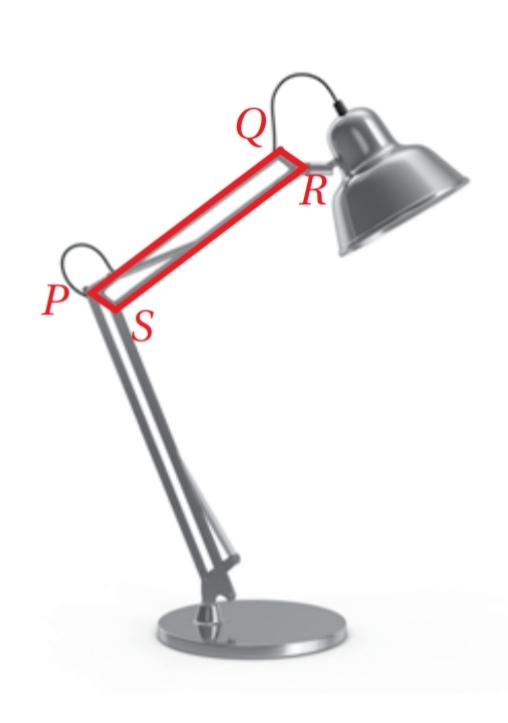
الحل :
..............................................................................................................................................................................................................
أتحقق من فهمي :
إذا كان ABCD متوازي أضلاع ، فأجد قيمة كل من x و y :
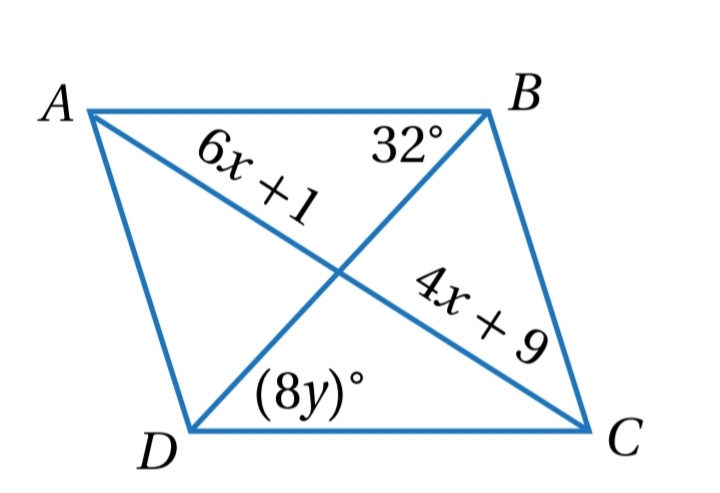
الحل :
بما أن قطرا متوازي الأضلاع ينصف كل منهما الاخر
بما أن قطر متوازي الاضلاع يقسمه الى مثلثين متطابقين
وبما أن الزوايا المتناظرة في المثلثات المتطابقة تكون متطابقة :
........................................................................................................................................................................................................................................
أتحقق من فهمي :
في الشكل المجاور ، إذا كان ABCD و GDEF متوازيي أضلاع ، فأثبت أن باستعمال البرهان ذي العمودين
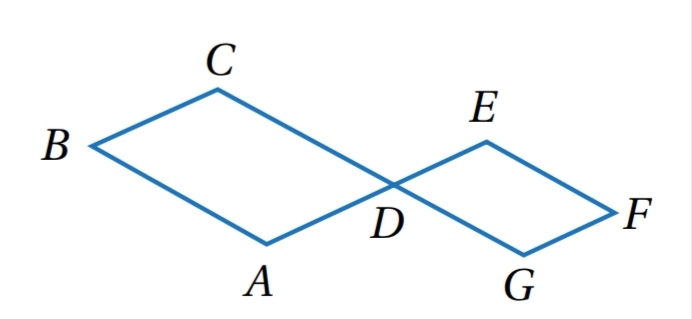
الحل :
| المبررات | العبارات |
| 1- معطى | 1- ABCD, GDEF متوازيي أضلاع |
| 2- زاويتان متقابلتان بالرأس | 2- |
| 3- الزوايا المتقابلة في متوازي الاضلاع متطابقة | 3- |
| 4- نتيجة | 4- |
..............................................................................................................................................................................................................
حل تمارين ومسائل الدرس :
اتدرب وأحل المسائل :
أكمل كل جملة مما يأتي في ما يتعلق ب مبرراً إجابتي :

حسب نظرية الزوايا المتقابلة في متوازي الاضلاع
........................................................................................................................................................................................................................................
قطر متوازي الاضلاع يقسمه الى مثلثين متطابقين والزوايا المتناظرة في المثلثات المتطابقة متطابقة
........................................................................................................................................................................................................................................
كل ضلعين متقابلين في متوازي الاضلاع متوازيان
........................................................................................................................................................................................................................................
كل ضلعين متقابلين في متوازي الاضلاع متوازيان
........................................................................................................................................................................................................................................
قطر متوازي الاضلاع يقسمه الى مثلثين متطابقين
........................................................................................................................................................................................................................................
قطر متوازي الاضلاع يقسمه الى مثلثين متطابقين
........................................................................................................................................................................................................................................
7)
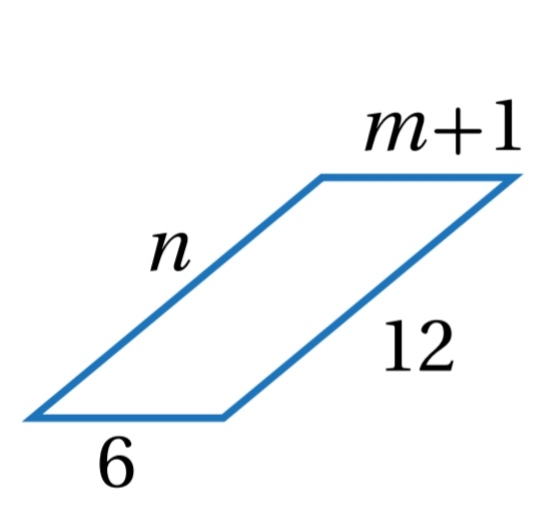
حسب نظرية الاضلاع المتقابلة في متوازي الاضلاع
........................................................................................................................................................................................................................................
8)
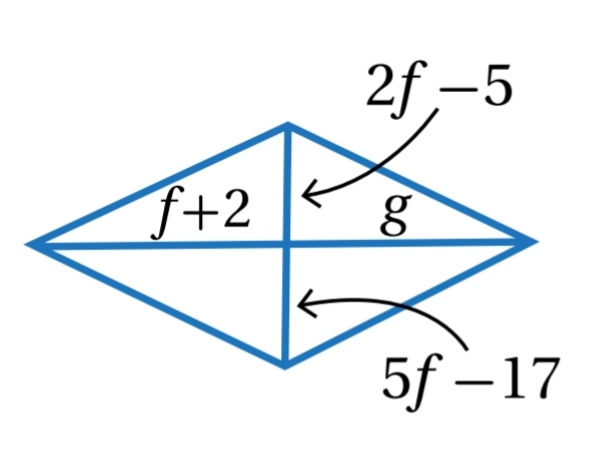
قطري متوازي الاضلاع ينصف كل منهما الاخر
قطري متوازي الاضلاع ينصف كل منهما الاخر
..............................................................................................................................................................................................................
9)
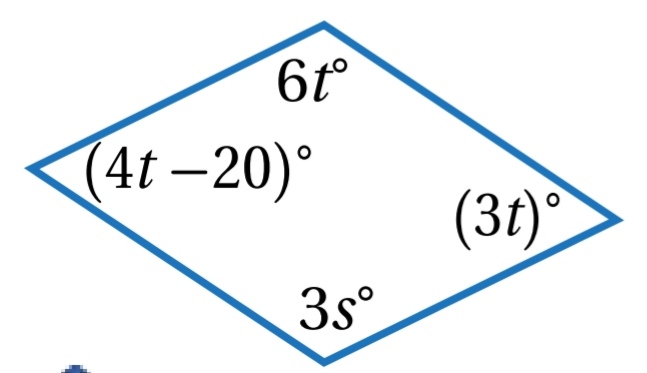
الزوايا المتقابلة في متوازي الاضلاع متطابقة
........................................................................................................................................................................................................................................
رافعة: استعمل الشكل المجاور الذي يبين رافعة المقص للاجابة عن الاسئلة الاتية :
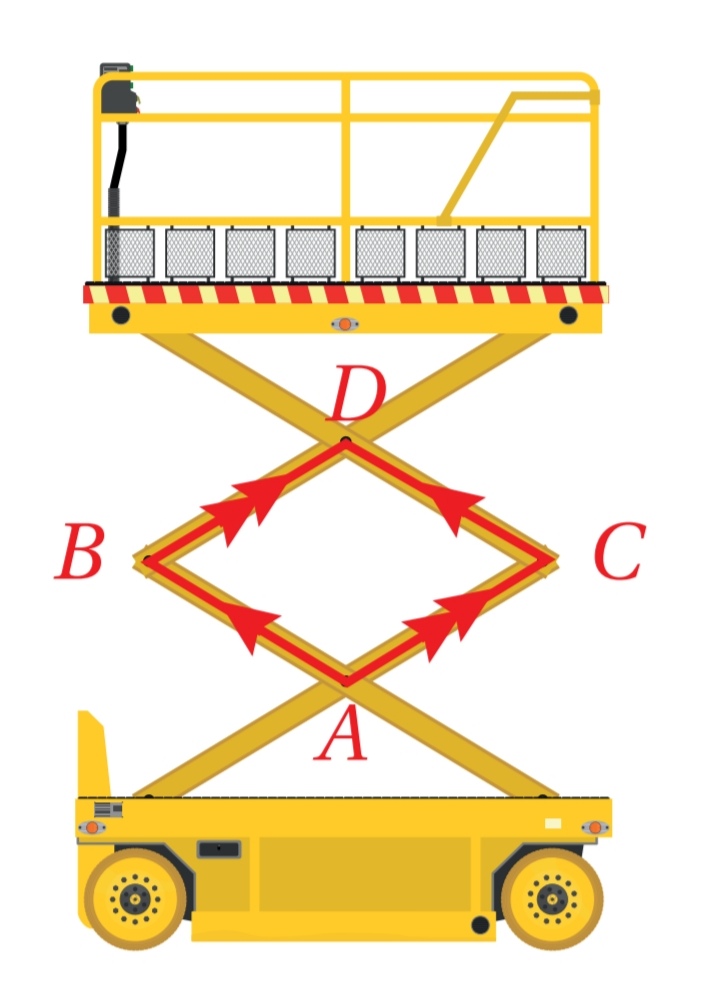
10 ) إذا كان ، فأجد
الحل :
بما أن ، زاويتان متحالفتان في متوازي الاضلاع إذن :
11) إذا قل ، فما تأثير ذلك في ؟
الحل : بما أن
حسب نظرية الزاويتان المتحالفتان في متوازي الاضلاع
إذن كلما قل زاد
12) إذا قل ، فما تأثير ذلك في طول AD ؟
كلما قل زاد طول AD
13) إذا قل ، فما تأثير ذلك في ارتفاع الرافعة ؟
كلما قل كلما زاد ارتفاع الرافعة
........................................................................................................................................................................................................................................
14) في الشكل الآتي، إذا كان GDKH متوازي أضلاع ، فأستعمل المعلومات المعطاة على الشكل ، لأثبت أن باستعمال البرهان ذي العمودين .
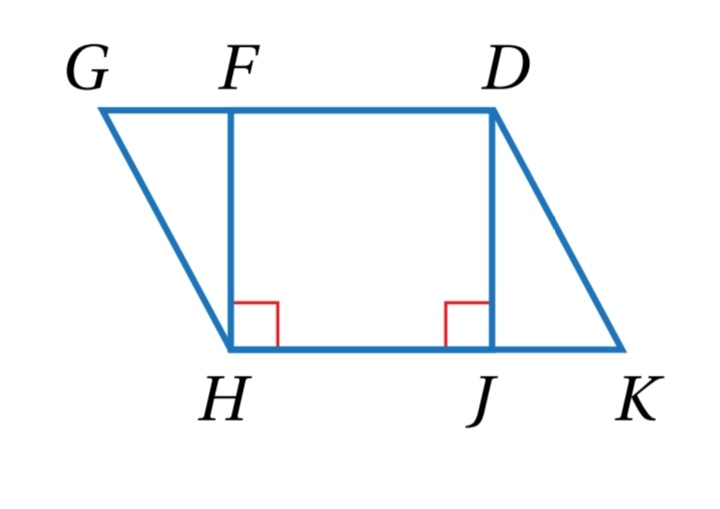
الحل:
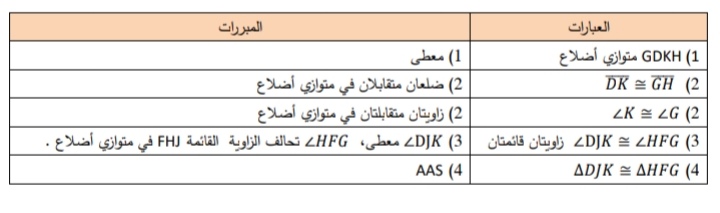
........................................................................................................................................................................................................................................
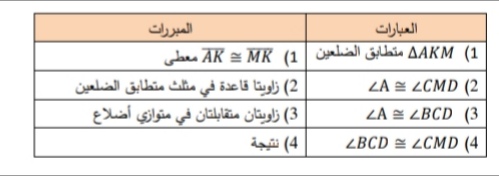
15) في الشكل الآتي ، إذا كان ABCD متوازي أضللاع و ، فأثبت أن باستعمال البرهان ذي العمودين.
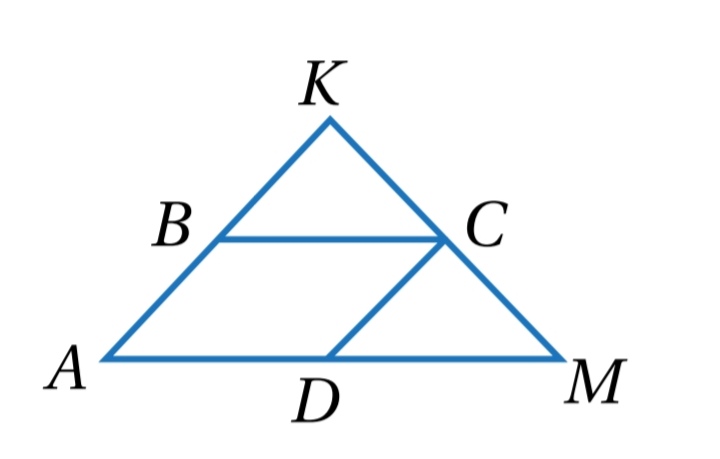
الحل :
........................................................................................................................................................................................................................................
16) أكتشف الخطأ: أنظر الحل الآتي ، وأكتشف الخطأ الوارد فيه ، وأصححه.
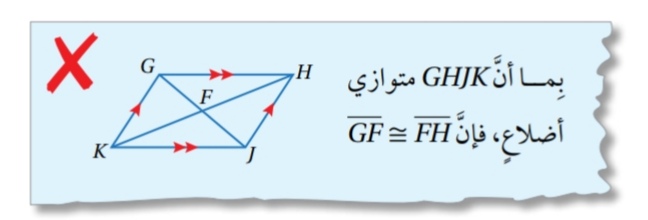
الخطأ : العبارة خاطئة
والصحيح :
لأن في متوازي الاضلاع كل قطر ينصف القطر الاخر
........................................................................................................................................................................................................................................
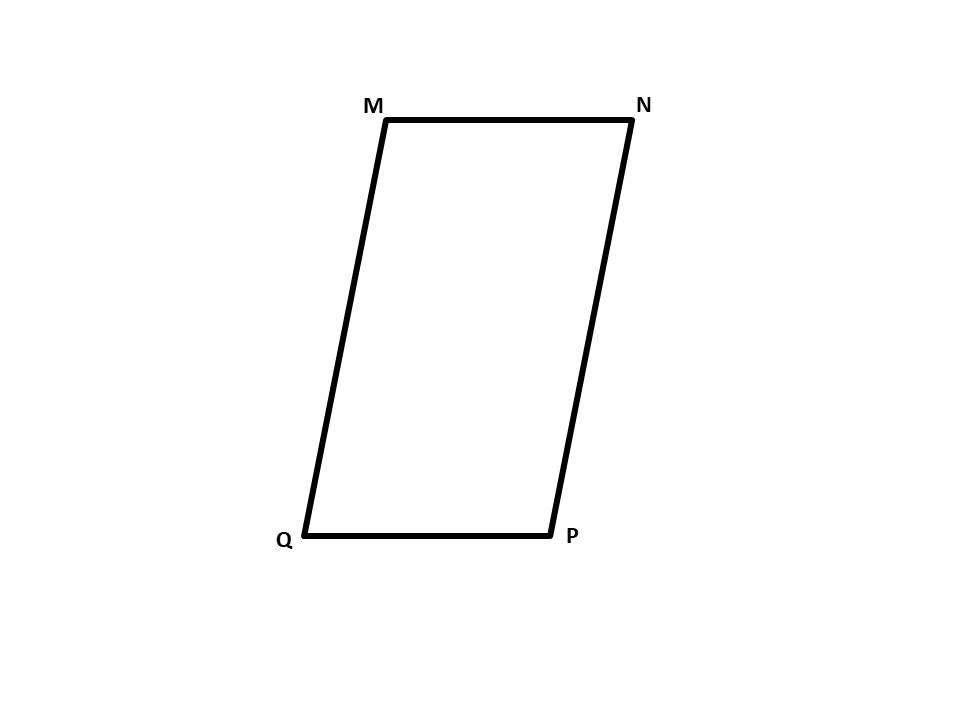
17) تبرير : تمثل المقادير الجبرية أدناه أطوال أضلاع . أجد محيط متوازي الاضلاع ، مبرراً إجابتي.
MQ = -2x + 37 QP = y + 14 NP = x - 5 MN = 4y + 5
الحل:
........................................................................................................................................................................................................................................
18) ما خصائص متوازي الاضلاع المتعلقة بزواياه وأضلاعه وأقطاره ؟
1- في متوازي الاضلاع كل ضلعين متقابلين متطابقين
2- في متوازي الاضلاع كل زاويتان متقابلتين متطابقتين
3- في متوازي الاضلاع كل زاويتين متحالفتين متكاملتين
4- في متوازي الاضلاع إذا كانت احدى الزوايا قائمة فإن باقي الزوايا قائمة
5- في متوازي الاضلاع كل قطر ينصف الاخر
6- في متوازي الاضلاع كل قطر يقسم متوازي الاضلاع الى مثلثين طبوقين
........................................................................................................................................................................................................................................
حل أسئلة كتاب التمارين :
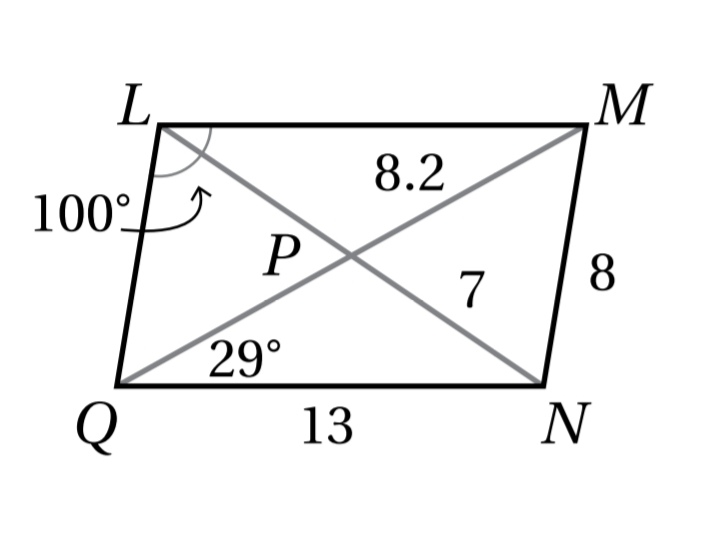
1- LM = 13
لأن كل ضلعين متقابلين في متوازي الاضلاع متطابقين
2- LP = 7
في متوازي الاضلاع كل قطر ينصف الاخر
3- LQ = 8
كل ضلعين متقابلين في متوازي الاضلاع متطابقين
4- MQ = 2 x 8.2 = 16.4
لأن كل قطر ينصف الاخر في متوازي الاضلاع
لأن الزاويتين متحالفتان متكاملتان في متوازي الاضلاع
لأن كل زاويتان متقابلتين متطابقتين في متوازي الاضلاع
لأن
لأن
قطر متوازي الاضلاع يقسمه الى مثلثين متطابقين والزوايا المتناظرة في المثلثات المتطابقة متطابقة
........................................................................................................................................................................................................................................
9) أجد قيمة كل من المتغيرين x و y في المجاور إذا كانت :

PT = x + 2 TR = y QT = 2x TS = y + 3
الحل :
أعلم أن قطرا متوازي الاضلاع كل منهما ينصف الاخر إذن :
أحل المعادلتين حلاً مشتركاً
بتعويض 2x - 3 في المعادلة الاولى بدلاً من نجد :
أجد قيم المتغيرات في كل من متوازيات الاضلاع الاتية :
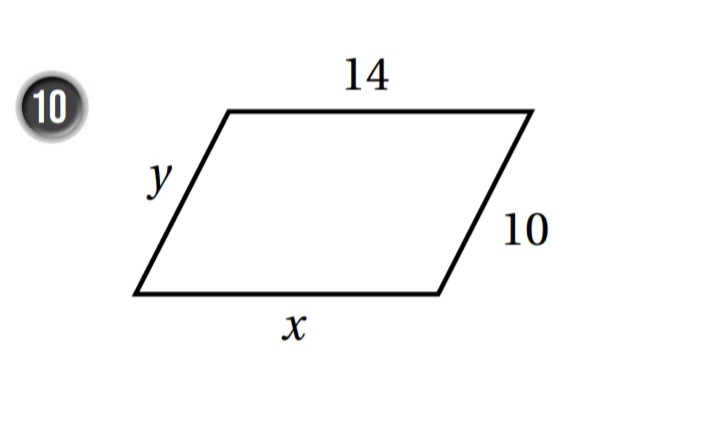
x = 14
y = 10

x = 12
3y + 1 = 10
3y = 10 - 1
3 y = 9
y = 3
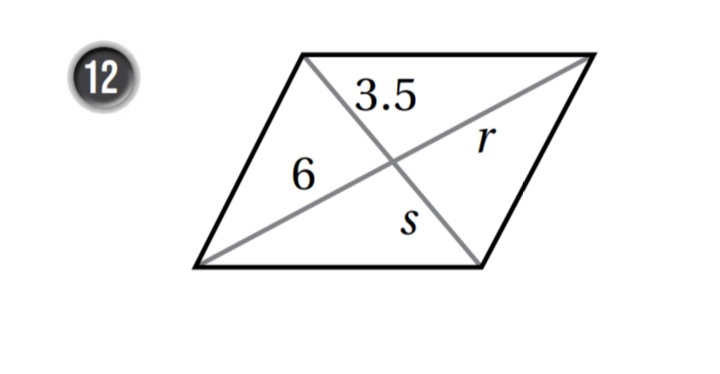
s = 3.5
r = 6
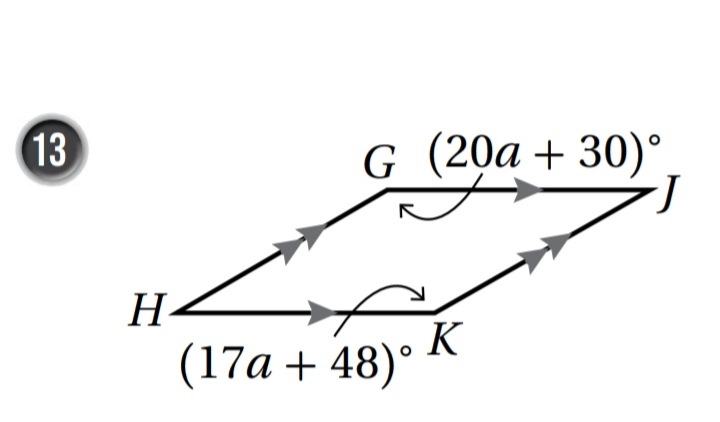
20a + 30 = 17a + 48
20a - 17a = 48 - 30
3a = 18
a = 6
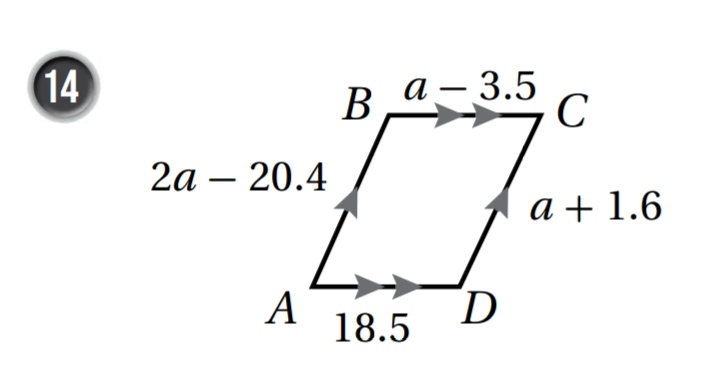
a - 3.5 = 18.5
a = 18.5 + 3.5
a = 22
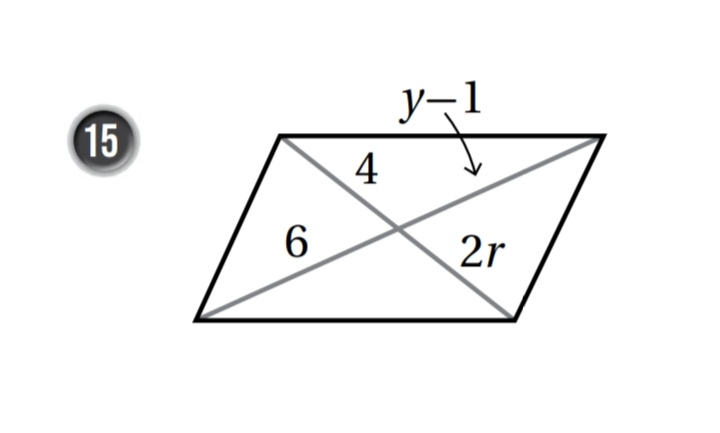
y - 1 = 6
y = 7
2r = 4
r = 2
....................................................................................................................................................................................................................................................................................................................
16) في الشكل الاتي إذا كان فأثبت أن باستعمال البرهان ذي العمودين
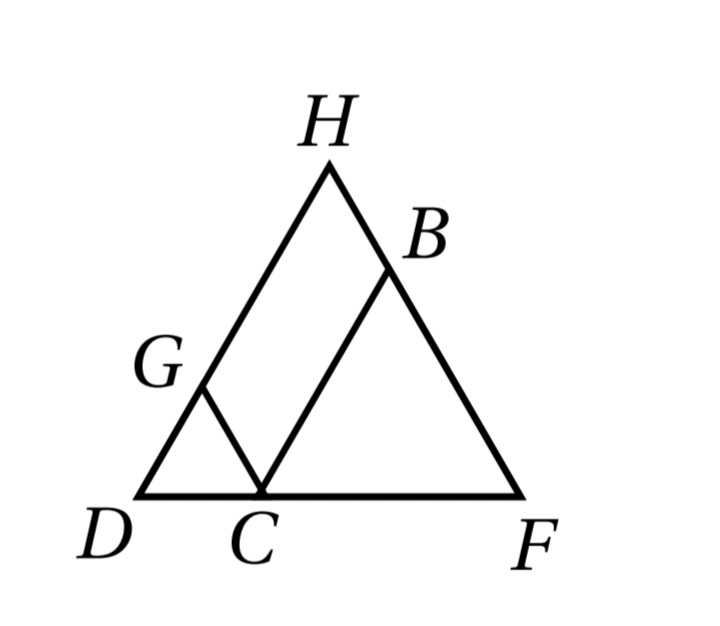
| المبررات | العبارات |
| معطى | |
| نتيجة | |
| زاويتا القاعدة في المثلث المتساوي الساقين متطابقة | |
| معطى | |
| زوايا متقابلة في متوازي الاضلاع لأن |
........................................................................................................................................................................................................................................................................................
17) في الشكل الاتي ، اذا كان متوازيي اضلاع ، فأثبت أن باستعمال البرهان ذي العمودين

| المبررات | العبارات |
| معطى | |
| كل زاويتين متقابلتين في متوازي الاضلاع متطابقتين | |
| معطى | |
| كل زاويتين متقابلتين في متوازي الاضلاع متطابقتين | |
| لأن |