رياضيات فصل ثاني

مفاهيم أساسية : 

يمكن حساب مساحة الدائرة (ِِA) بإستعمال النسبة التقريبية $\mathrm{\pi }$ وتساوي : ناتج ضرب $\mathrm{\pi }$ في مربَّعِ نصفِ القُطْرِ.

$\mathbf{A}\mathbf{=}{\mathbf{\pi r}}^{\mathbf{2}}$

 

مثال 1: أَجِدُ مساحةَ كلِّ دائرةٍ ممّا يأتي، وَأستعملُ الآلةَ الحاسبةَ لأتحقّقَ مِنْ صحةِ إجابتي

1)

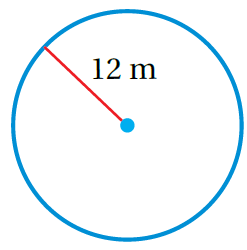
$\mathrm{A}={\mathrm{\pi r}}^2$                             صيغة مساحة الدائرة 

$$\begin{gathered} \approx 3.14 \times {\left(12\right)}^2 \\ \approx 452.16 \end{gathered}$$                                 بتعويض مربع نصف القطر و النسبة التقريبية π 

إذنْ، مساحةُ الدائرةِ تساوي 452.16m² تقريباً 

أستعملُ الآلةَ الحاسبةَ لأتحقّقَ مِنْ صحةِ إجابتي على النحوِ الآتي:

الإجابةُ قريبةٌ. إذنْ، إجابتي صحيحةٌ.

 

يمكنُ إيجادُ طولِ نصفِ قُطْرِ دائرةٍ أَوْ طولِ قُطْرِها إذا علمْتُ مساحتَها، بِاستعمالِ خطواتِ حلِّ المعادَلةِ.

مثال2: أَجِدُ طولَ نصفِ قُطْرِ دائرةٍ مساحتُها 1256cm² أستعمل 3.14$\mathbf{\pi }\mathbf{\approx }$ 

$\mathrm{A}={\mathrm{\pi r}}^2$                             صيغة مساحة الدائرة 

$1256 = 3.14\times r^2$                       تعويض النسبة التقريبية π و مساحة الدائرة                    

$$\begin{gathered} \frac{1256}{3.14} =\frac{ 3.14\times r^2}{3.14} \\ 400=r^2 \\ 20=r \end{gathered}$$                   بالقسمة على 3.14 ثم التبسيط 

20 cm إذنْ، طولُ نصفِ قُطْرِ الدائرةِ يساوي

 

يُمكنُ استخدامُ قانونِ مساحةِ الدائرةِ في مواقفَ حياتيةٍ متنوعةٍ وكثيرةٍ.

مثال 3: منَ الحياةِ: عملةٌ : يبلغُ قُطْرُ القطعةِ النقديةِ مِنْ فئةِ الخمسةِ قُروشٍ 26mm تقريبًا، أَجِدُ مساحةَ الوجهِ الظاهرِ منها، وَأقرّبُ إجابتي لِـأقربِ عددٍ صحيحٍ.

قطرُ القطعةِ النقديةِ 26mm  إذنْ، طولُ نصفِ قُطْرِها 13mm

$\mathrm{A}={\mathrm{\pi r}}^{2 }$                             صيغة مساحة الدائرة 

$$\begin{gathered} \approx 3.14\times {\left(13\right)}^2 \\ \approx 530.66 \\ \approx 531 \end{gathered}$$                             بتعويض النسبة التقريبية π ومربع نصف القطر    

إذنْ، مساحةُ الوجهِ الظاهرِ مِنَ القطعةِ النقديةِ يساوي 531m² تقريبًا