مفاهيم أساسية
الهَرَمُ المنتظمُ (Regular pyramid) :هَرَمٌ قاعدتُهُ مضلَّعٌ منتظمٌ، وَأوجهُهُ الجانبيةُ مثلَّثاتٌ متطابقةٌ كلٌّ منها متطابقُ الضِّلعَينِ، وَارتفاعُ كلِّ مثلَّثٍ يُسمّى الارتفاعَ الجانبيَّ ( l)لِلهَرَمِ (Slant high).
عندَ إعادةِ ترتيبِ الأوجُهِ الجانبيةِ لِلهَرَمِ المنتظَمِ؛ فإنَّها تشكّلُ نصفَ مستطيلٍ طولُهُ يساوي محيطَ قاعدةِ الهَرَمِ، وعرضُهُ مُساوٍ لارتفاعِ الهَرَمِ الجانبيِّ، وَعليْهِ، فإنَّ مساحةَ سطحِ الهَرَمِ الجانبيةَ تساوي نصفَ محيطِ القاعدةِ مضروبًا في ارتفاعِهِ الجانبيِّ.
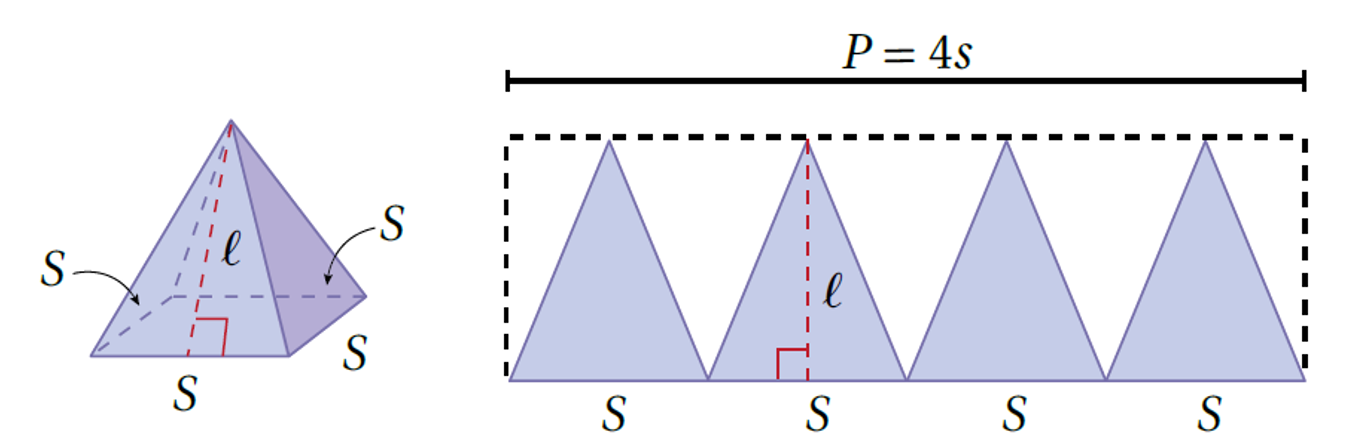
المساحةُ الجانبيةُ وَالمساحةُ الكلّيةُ لِسطحِ الهَرَمِِ :
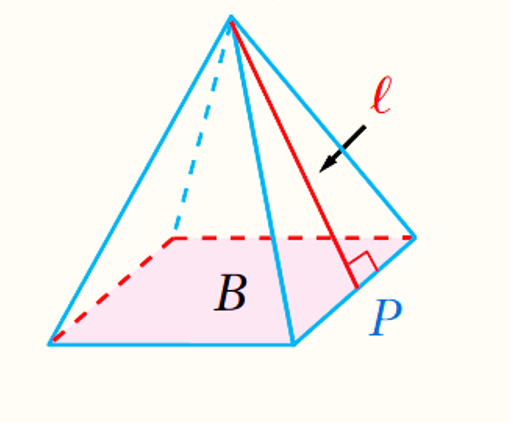
المساحةُ الجانبيةُ لِسطحِ الهَرَمِ المنتظَمِ تساوي : نصفَ محيطِ القاعدةِ(P) مضروبًا في الارتفاعِ الجانبيِّ (l)
المساحةُ الكلّيةُ لِسطحِ الهَرَمِ المنتظَمِ تساوي : مجموعَ مساحتِهِ الجانبيةِ وَمساحةِ قاعدتِهِ (B)
مثال 1: أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ هَرَمٍ منتظَمٍ ممّا يأتي:
1)
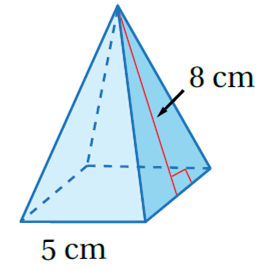
الْخُطْوَةُ 1: أَجِدُ محيطَ القاعدةِ وَمساحتَها:
P = 4 × 5 = 20 القاعدة مربعة p = 4 × s
B = 52 = 25 مساحةُ القاعدةِ B=s2
الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ الهَرَمِ المنتظَمِ:
صيغةُ المساحةِ الجانبيةِ لِسطحِ الهَرَمِ
بتعويض الأبعاد نجد الناتج
إذنْ، المساحةُ الجانبيةُ لِسطحِ الهَرَمِ تساوي 80cm2
الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ الهَرَمِ المنتظَمِ:
S.A = L.A + B صيغةُ المساحةِ الكلّيةِ لِسطحِ الهَرَمِ
25+80 = بتعويض الأبعاد نجد الناتج
105=
إذنْ، المساحةُ الكلّيةُ لِسطحِ الهَرَمِ المنتظَمِ تساوي 105cm2
يُمكنُنا استخدامُ قانونِ المساحةِ الكلّيةِ لِسطحِ الهَرَمِ في مواقفَ حياتيةٍ كثيرةٍ وَمتنوِّعةٍ.
مثال 2: منَ الحياةِ: منزلٌ: يظهرُ في الشكلِ المجاورِ سقفُ منزلٍ على شكلِ هَرَمٍ رباعيٍّ منتظَمٍ، يُرادُ تغطيتُهُ بِقطعٍ خشبيةٍ مساحةُ كلٍّ منها 2.5m2 . كَمْ قطعةً خشبيةً نحتاجُ لِتغطيةِ السقفِ؟
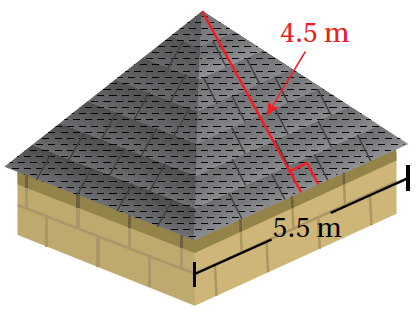
أَجِدُ المساحةَ الجانبيةَ لِسطحِ الهَرَمِ:
P = 4 × 5.5 = 22 القاعدة مربعة p = 4 × s
صيغةُ المساحةِ الجانبيةِ لِسطحِ الهَرَمِ
بتعويض الأبعاد نجد الناتج
إذنْ، المساحةُ الجانبيةُ لِلسطحِ تساوي 49.5m2
وَبما أنَّ القطعةَ الخشبيةَ الواحدةَ تغطّي مساحةَ 2.5m2 فَيمكنُ إيجادُ عددِ القِطعِ الّتي نحتاجُها لتغطيةِ السطحِ بِقسمةِ مساحةِ السطحِ على مساحةِ القطعةِ الخشبيةِ الواحدةِ:
49.5 ÷ 2.5 = 19.8
إذنْ، نحتاجُ 20 قطعةً خشبيةً تقريبًا لِتغطيةِ سطحِ المنزلِ.
مفهوم أساسي:
المساحةَ الجانبيةَ لِلمخروطِ تساوي نصفَ محيطِ قاعدتِهِ في ارتفاعِهِ الجانبيِّ، وَ مساحتَهُ الكلّيةَ هِيَ مجموعُ المساحةِ الجانبيةِ وَمساحةِ قاعدتِهِ.
المساحةُ الجانبيةُ وَالمساحةُ الكلّيةُ لِسطحِ المخروطِ :
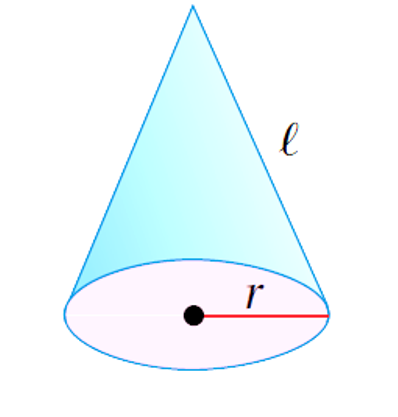
المساحةُ الجانبيةُ لِسطحِ المخروطِ تساوي: ناتجَ ضربِ نصفِ محيطِ قاعدةِ مخروطٍ طولُ نصفِ قُطرِها (r) في الارتفاعِ الجانبيِّ (ℓ) له
المساحةُ الكلّيةُ لِسطحِ المخروطِ فَتُساوي: مجموعَ مساحتِهِ الجانبيةِ وَمساحةِ القاعدةِ.
مثال 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ مخروطٍ ممّا يأتي، وَأقرّبُ الإجابةَ لِأقربِ جزءٍ مِنْ عشرةٍ:
1)
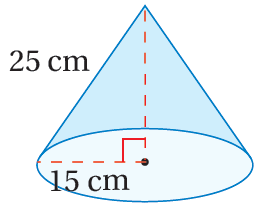
الْخُطْوَةُ 1: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المخروطِ:
صيغةُ المساحةِ الجانبيةِ لِسطحِ المخروطِ
بتعويض الأبعاد نجد الناتج
إذنْ، المساحةُ الجانبيةُ لِسطحِ المخروطِ تساوي1178.1cm2
الْخُطْوَةُ 2 : أَجِدُ مساحةَ القاعدةِ:
B = πr2 صيغةُ مساحةِ الدائرةِ
π(152)= بتعويض نصف القطر نجد الناتج
≈ 706.9
إذنْ، مساحةُ القاعدةِ 706.9cm2
الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ المخروطِ:
S.A = L.A + B صيغةُ مساحةِ سطحِ المخروطِ
1178.1+706.9 = بتعويض الابعاد نجد الناتج
1885 =
إذنْ، المساحةُ الكلّيةُ لِسطحِ المخروطِ تساوي 1885cm2 تقريباً
يُمكنُنا استخدامُ قانونِ المساحةِ الكلّيةِ لِسطحِ المخروطِ في مواقفَ حياتيةٍ كثيرةٍ وَمتنوِّعةٍ.
مثال 4: منَ الحياةِ: كيمياءُ: تُستخدَمُ في بعضِ التجاربِ الكيميائيةِ أقماعٌ على شكلِ مخروطٍ يوضَعُ بِداخلِها ورقُ ترشيحٍ. أَجِدُ مساحةَ ورقِ الترشيحِ اللازمةَ لِلقُمعِ المجاورِ. أقرّبُ إجابتي لِأقربِ جزءٍ مِنْ عشرةٍ.
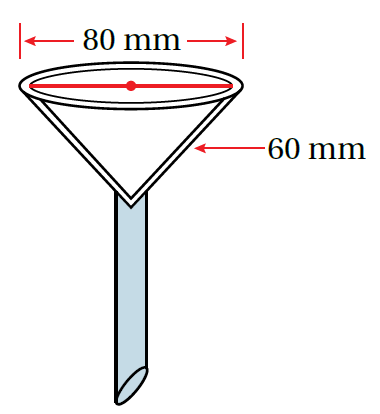
أَجِدُ المساحةَ الجانبيةَ لِسطحِ المخروطِ:
L.A = πrℓ صيغةُ المساحةِ الجانبيةِ لِسطحِ المخروطِ
π (40)(60) = بتعويض الأبعاد نجد الناتج
7539.8≈
إذنْ، مساحةُ ورقِ الترشيحِ تساوي 7539.8cm2 تقريبًا.